5.2 探索轴对称的性质同步练习

21世纪教育网 –中小学教育资源及组卷应用平台
5.2 探索轴对称的性质同步练习
　班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.轴对称的性质:
①对应点所连的线段被对称轴垂直平分．②对应线段 相等,对应角相等．
2.轴对称的性质“对应点所连的线段被对称轴垂直平分”包含的两层含义:一是对应点在对称轴的同一条垂线上;二是对应点到对称轴的距离相等．【来源：21cnj*y.co*m】
基础知识和能力拓展精练
一、选择题
1．两个图形关于某条直线对称，对称点一定在（ ）
A. 这条直线的两旁 B. 这条直线的同旁 C. 这条直线上 D. 这条直线上或两旁
2．下列语句中，正确的有( ）
①两点的连线被某条直线平分，则这两点是关于该直线成轴对称的点；
②形状、大小相同的两个图形一定成轴对称；
③如果一个图形沿着某条直线对折后，不能和另一个图形重合，那么这两个图形一定不成轴对称；
④成轴对称的两个图形的面积相等.
A. 1个 B. 2个 C. 3个 D. 4个
3．如图，△ABC与△DEF关于直线MN轴对称，则以下结论中错误的是（　　）
( http: / / www.21cnjy.com / )
A. AB∥DF B. ∠B=∠E C. AB=DE D. AD的连线被MN垂直平分
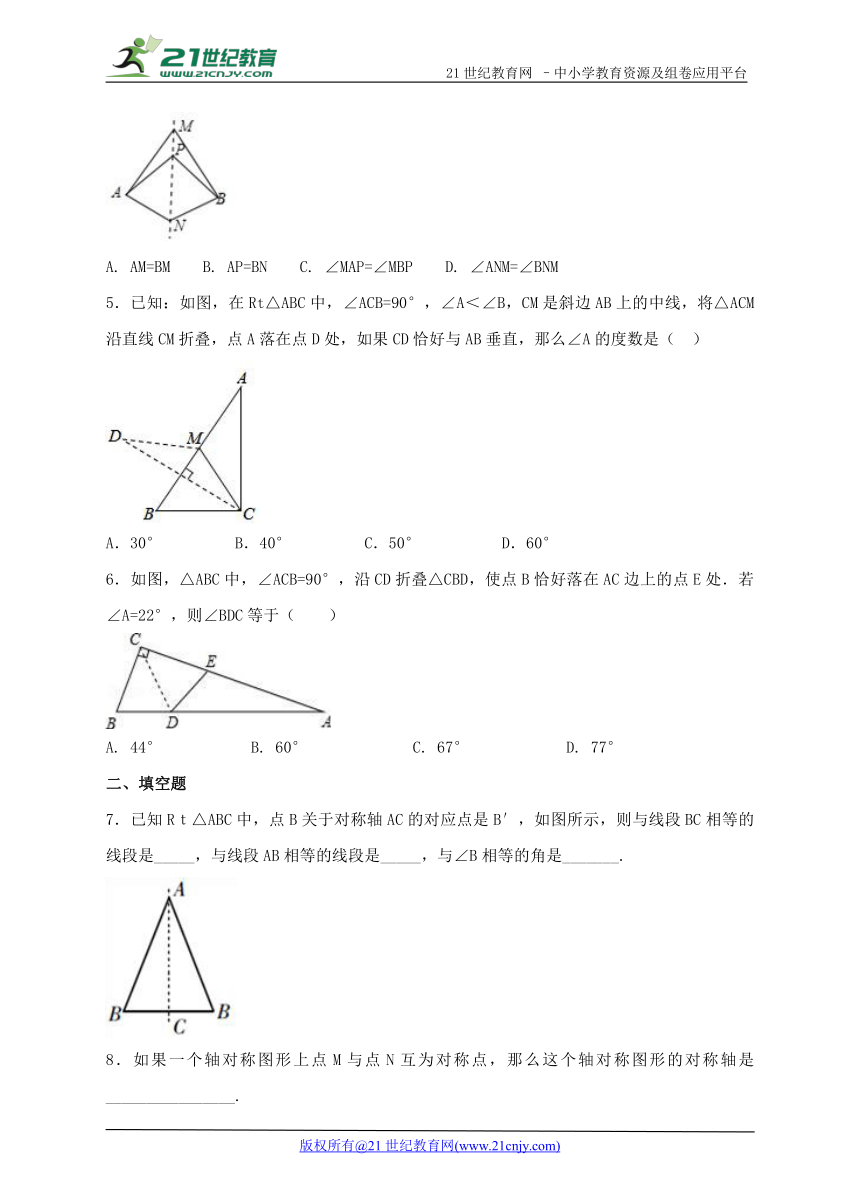
4．如图，直线MN是四边形AMBN的对称轴，点P是直线MN上的点，下列判断错误的是（　　）
( http: / / www.21cnjy.com / )
A. AM=BM B. AP=BN C. ∠MAP=∠MBP D. ∠ANM=∠BNM【出处：21教育名师】
5．已知：如图，在Rt△ABC中，∠AC ( http: / / www.21cnjy.com )B=90°，∠A＜∠B，CM是斜边AB上的中线，将△ACM沿直线CM折叠，点A落在点D处，如果CD恰好与AB垂直，那么∠A的度数是（ ）
A．30° B．40° C．50° D．60°
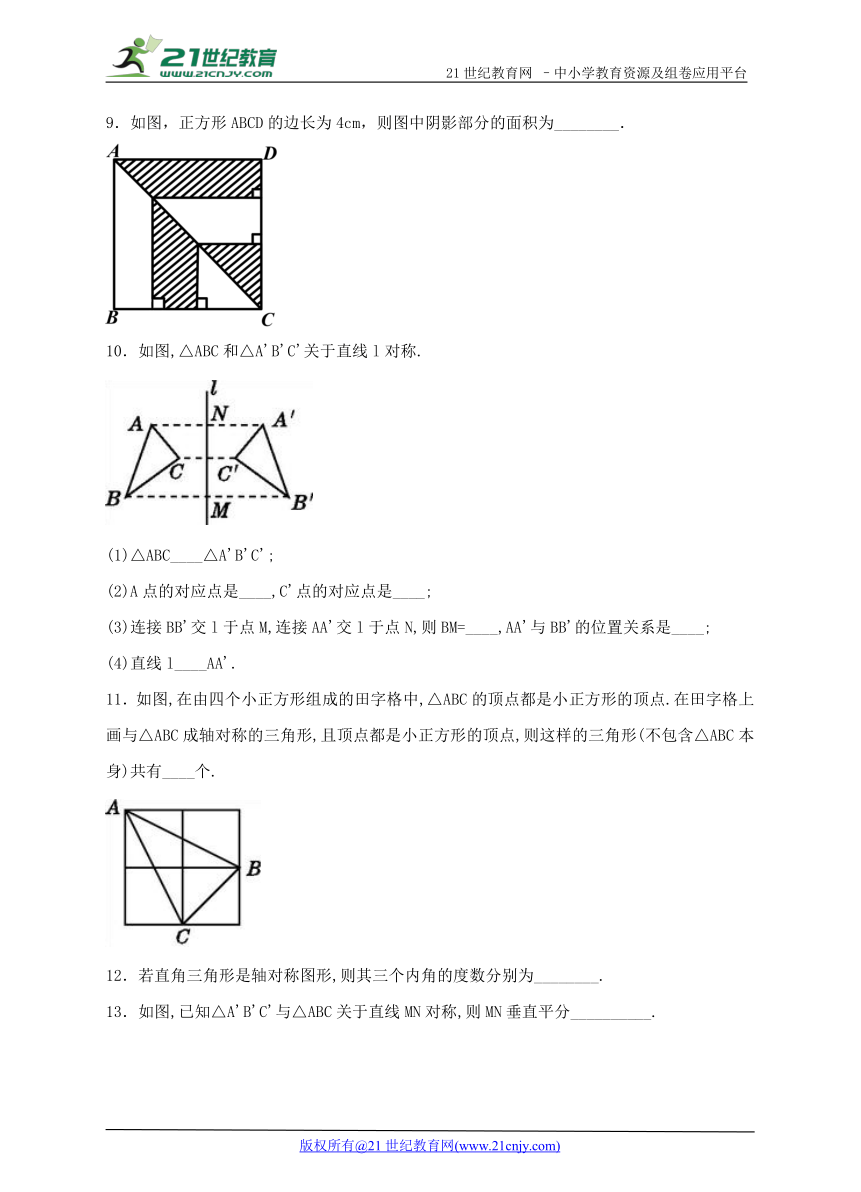
6．如图，△ABC中，∠ACB=90°，沿CD折叠△CBD，使点B恰好落在AC边上的点E处．若∠A=22°，则∠BDC等于（　　）2-1-c-n-j-y
( http: / / www.21cnjy.com / )
A. 44° B. 60° C. 67° D. 77°
二、填空题
7．已知Rｔ△ABC中，点B关于对称轴AC ( http: / / www.21cnjy.com )的对应点是B′，如图所示，则与线段BC相等的线段是_____，与线段AB相等的线段是_____，与∠B相等的角是_______.
( http: / / www.21cnjy.com / )
8．如果一个轴对称图形上点M与点N互为对称点，那么这个轴对称图形的对称轴是________________.【版权所有：21教育】
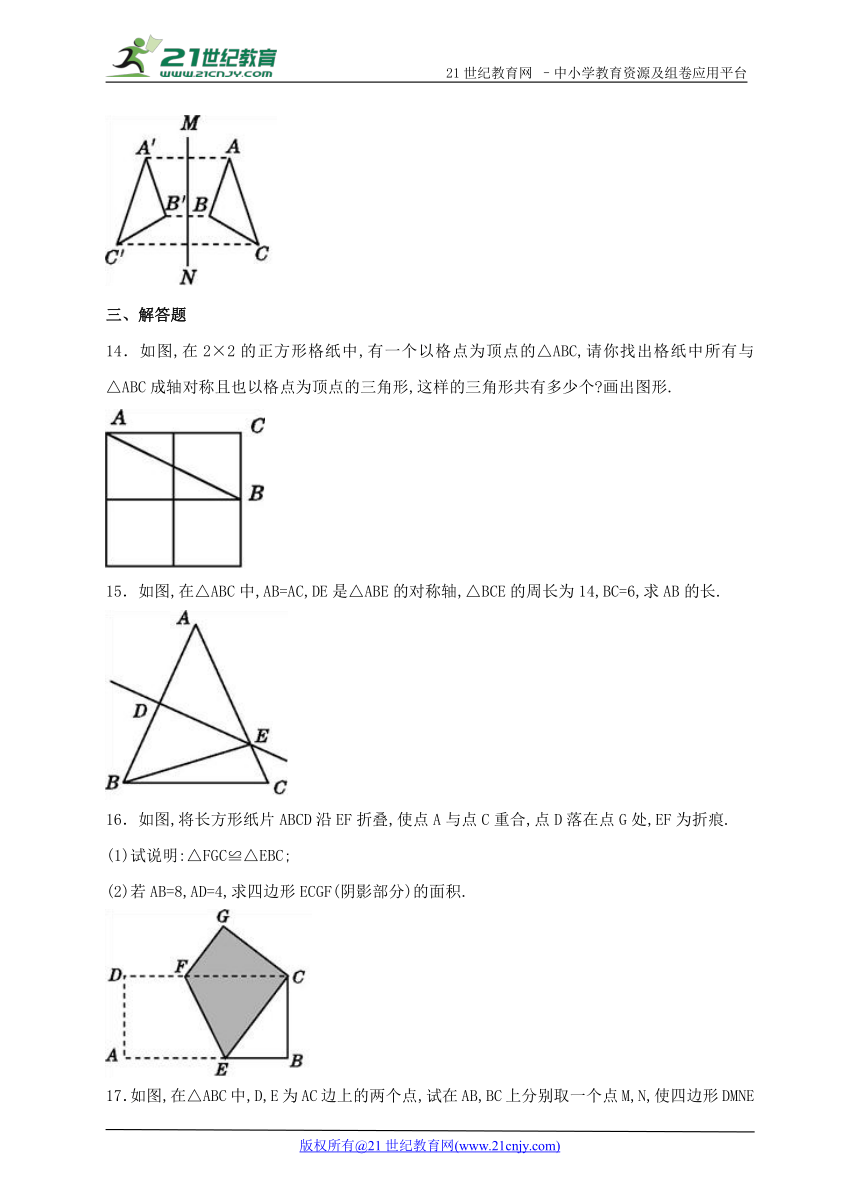
9．如图，正方形ABCD的边长为4cm，则图中阴影部分的面积为________．
10．如图,△ABC和△A'B'C'关于直线l对称.
( http: / / www.21cnjy.com / )
(1)△ABC____△A'B'C';
(2)A点的对应点是____,C'点的对应点是____;
(3)连接BB'交l于点M,连接AA'交l于点N,则BM=____,AA'与BB'的位置关系是____;
(4)直线l____AA'.
11．如图,在由四个小正方形组成的田字格中 ( http: / / www.21cnjy.com ),△ABC的顶点都是小正方形的顶点.在田字格上画与△ABC成轴对称的三角形,且顶点都是小正方形的顶点,则这样的三角形(不包含△ABC本身)共有____个.21教育名师原创作品
( http: / / www.21cnjy.com / )
12．若直角三角形是轴对称图形,则其三个内角的度数分别为________.
13．如图,已知△A'B'C'与△ABC关于直线MN对称,则MN垂直平分__________.
( http: / / www.21cnjy.com / )
三、解答题
14．如图,在2×2的正方 ( http: / / www.21cnjy.com )形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且也以格点为顶点的三角形,这样的三角形共有多少个 画出图形.
( http: / / www.21cnjy.com / )
15．如图,在△ABC中,AB=AC,DE是△ABE的对称轴,△BCE的周长为14,BC=6,求AB的长.
( http: / / www.21cnjy.com / )
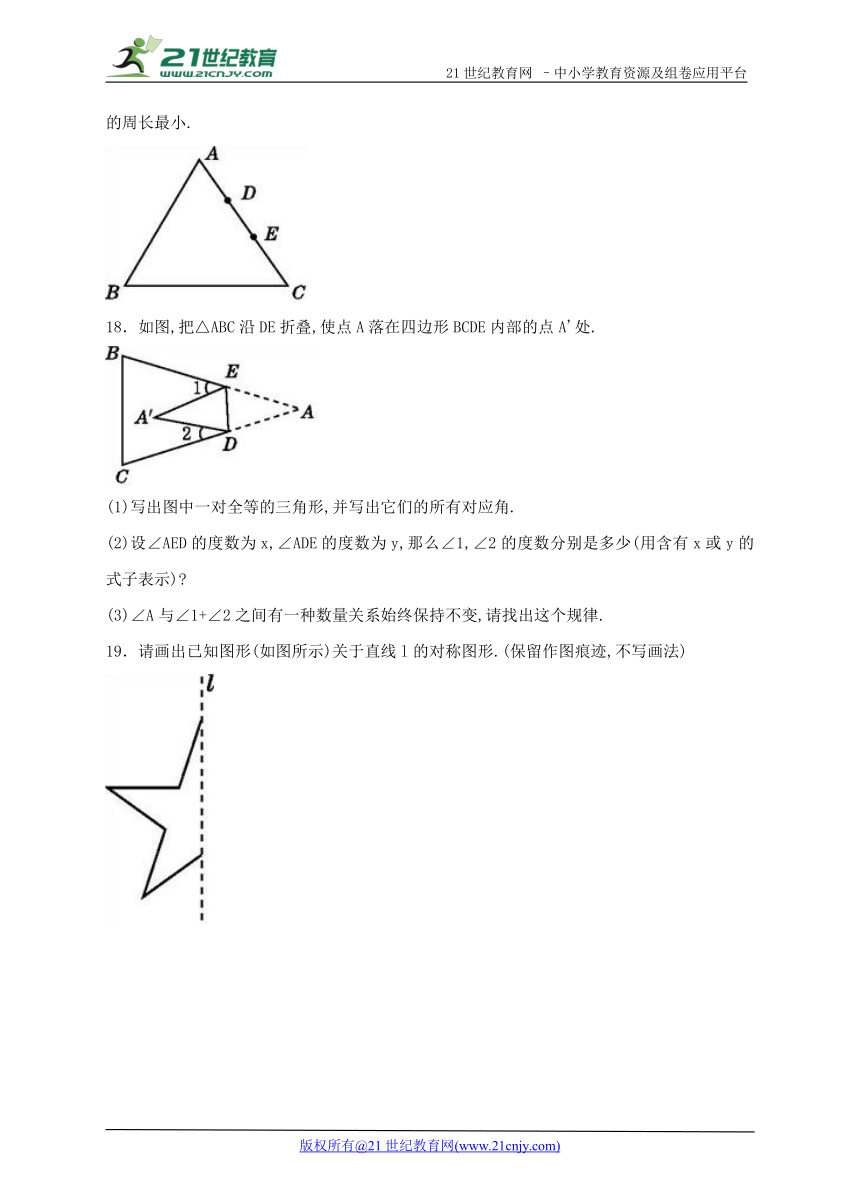
16．如图,将长方形纸片ABCD沿EF折叠,使点A与点C重合,点D落在点G处,EF为折痕.
(1)试说明:△FGC≌△EBC;
(2)若AB=8,AD=4,求四边形ECGF(阴影部分)的面积.
( http: / / www.21cnjy.com / )
17．如图,在△ABC中,D,E为AC边上的两个点,试在AB,BC上分别取一个点M,N,使四边形DMNE的周长最小.21*cnjy*com
( http: / / www.21cnjy.com / )
18．如图,把△ABC沿DE折叠,使点A落在四边形BCDE内部的点A'处.
( http: / / www.21cnjy.com / )
(1)写出图中一对全等的三角形,并写出它们的所有对应角.
(2)设∠AED的度数为x,∠ADE的度数为y,那么∠1,∠2的度数分别是多少(用含有x或y的式子表示)
(3)∠A与∠1+∠2之间有一种数量关系始终保持不变,请找出这个规律.
19．请画出已知图形(如图所示)关于直线l的对称图形.(保留作图痕迹,不写画法)
( http: / / www.21cnjy.com / )
参考答案
1．D
【解析】两个图形关于某条直线对称，对称点一定在这条直线上或两旁.故选D.
2．A
【解析】①两点的连线被某条直线平分，则这两点是关于该直线成轴对称的点；错误；
②形状、大小相同的两个图形一定成轴对称；错误；
③如果一个图形沿着某条直线对折后，不能和另一个图形重合，那么这两个图形一定不成轴对称；错误，关键是看这条直线是否为对称轴了；
④成轴对称的两个图形的面积相等.正确，成轴对称的两个图形一定是全等的.故面积相等.
故选A.
3．A
【解析】A选项无法判断；B. ∠B=∠E 、C. AB=DE 、 D. AD的连线被MN垂直平分均可以由成轴对称的两个图形的性质得到.21cnjy.com
4．D
【解析】试题解析：∵直线MN是四边形AMBN的对称轴，
∴点A与点B对应，
∴AM=BM，AN=BN，∠ANM=∠BNM，
∵点P时直线MN上的点，
∴∠MAP=∠MBP，
∴A，C，D正确，B错误，
故选B．
5．A.
【解析】
试题解析：如图，
∵CM是斜边AB上的中线，
∴CM=AM=AB，
∴∠A=∠MCA（设为α）；
由翻折变换的性质得：∠DCM=∠MCA=α；
∵CD⊥AB，
∴∠DCA+∠A=90°，
即3α=90°，
∴∠A=α=30°．
故选A.
考点：翻折变换（折叠问题）．
6．C
【解析】试题分析：由∠ACB=90°，∠A=22°，三角形内角和是180 ，可得∠B=90 -22 =68 ，因为折叠角相等，所以∠CED=∠B=68 ，∠BDC=∠EDC= ( http: / / www.21cnjy.com / )∠BDE，，因为四边形内角和是360 ，所以∠BDE=360 -90 -68 -68 =134 ，所以∠BDC= ( http: / / www.21cnjy.com / )∠BDE= ( http: / / www.21cnjy.com / )×134 =67 ．故选C．
考点：1．折叠性质；2．四边形内角和．
7． B′C， AB′， ∠B′
【解析】根据轴对称图形的性质得，与线段BC相等的线段是B′C，与线段AB相等的线段是AB′，与∠B相等的角是∠B′.21世纪教育网版权所有
故答案：(1). B′C， (2). AB′， (3). ∠B′
8．线段MN的垂直平分线
【解析】如果一个轴对称图形上点M与点N互为对称点，那么这个轴对称图形的对称轴是
线段MN的垂直平分线.
故答案：线段MN的垂直平分线 .
9．8cm2
【解析】阴影部分的面积等于正方形面积的一半．
10． （1）≌ (2) A'点 C点 （3）B'M 互相平行 （4）垂直平分
【解析】根据轴对称的性质：关于某条直线 ( http: / / www.21cnjy.com )对称的两个图形是全等图形；如果两个图形关于某直线对称，那么对称轴是对应点连线的垂直平分线；两个图形关于某直线对称，如果它们的对应线段或延长线相交，那么交点在对称轴上.由此可得：(1)△ABC≌△A'B'C'; (2)A点的对应点是点A',C'点的对应点是点C; (3)连接BB'交l于点M,连接AA'交l于点N,则BM= B'M,AA'与BB'的位置关系是互相平行; (4)直线l垂直平分AA'.www.21-cn-jy.com
11．3
【解析】如图所示,符合条件的点共有3个.
( http: / / www.21cnjy.com / )
12．90°45°45°
【解析】∵直角三角形是轴对称图形 ，
∴一定有两个角相等.
又∵直角三角形一定有一个角为90°，
∴相等的是两个锐角.
∵直角三角形的两个锐角互余，
∴每一个锐角为45°.
13．AA',BB',CC'
【解析】已知△ABC与△A′B′C ( http: / / www.21cnjy.com )′关于直线MN对称，根据轴对称的性质，对应点的连线被对称轴垂直平分可得MN垂直平分线段AA′、线段BB′、线段CC′．
故答案为：线段AA′、线段BB′、线段CC′．
14．5个,图形见解析
【解析】试题分析：根据轴对称的定义画出图形即可，注意不要漏画图形.
试题解析：
如图,与△ABC成轴对称且也以格点为顶点的三角形有5个.
( http: / / www.21cnjy.com / )
15．8
【解析】试题分析：由DE是△ABE ( http: / / www.21cnjy.com )的对称轴，根据轴对称的性质可得AE=BE，再由C△BCE=BC+CE+BE=14，可得BC+AC=14，从而求得AB的长.21·cn·jy·com
试题解析：
因为DE是△ABE的对称轴,
所以AE=BE.
所以C△BCE=BC+CE+BE=BC+CE+AE=BC+AC=14.
因为BC=6,所以AC=8.
所以AB=AC=8.
16．(1)见解析；（2）16
【解析】试题分析：（1）先证∠GCF=∠BC ( http: / / www.21cnjy.com )E，根据折叠性质，GC=AD=BC，∠G=∠D=∠B=90°根据ASA判定全等即可；（2）由（1）可知，阴影面积=四边形BCFE面积=矩形面积的一半，计算即可．2·1·c·n·j·y
试题解析：
(1)因为∠GCF+∠FCE=90°,∠FCE+∠BCE=90°,
所以∠GCF=∠BCE.
又因为∠G=∠B=90°,GC=BC,
所以△FGC≌△EBC.
(2)由(1)知,DF=GF=BE,
所以四边形ECGF的面积=四边形AEFD的面积===16.
17．见解析
【解析】试题分析：作点D关 ( http: / / www.21cnjy.com )于直线AB的对称点D',作点E关于直线BC的对称点E'.连接D'E'交AB于点M,交BC于点N.连接DM,EN.四边形DMNE就是符合要求的四边形.
试题解析：
如图,(1)作点D关于直 ( http: / / www.21cnjy.com )线AB的对称点D',作点E关于直线BC的对称点E'.(2)连接D'E'交AB于点M,交BC于点N.(3)连接DM,EN.【来源：21·世纪·教育·网】
四边形DMNE就是符合要求的四边形,此时周长最小.
( http: / / www.21cnjy.com / )
点睛：本题主要考查了轴对称最短路线应用以及轴对称的性质，得出M、N点位置是解题关键．
18．（1）△EAD≌△EA'D,其中 ( http: / / www.21cnjy.com )∠EAD=∠EA'D,∠AED=∠A'ED,∠ADE=∠A'DE.（2）∠1=180°-2x,∠2=180°-2y；（3）∠1+∠2=2∠A21·世纪*教育网
【解析】试题分析：（1）由轴对称的性质 ( http: / / www.21cnjy.com )即可得结论；（2）结合（1）的结论，根据平角的定义可得结论；（3）表示出图中的△ABC、△ADE的内角和以及四边形BCDE的内角和，整理化简即可得到所求角之间的关系．www-2-1-cnjy-com
试题解析：
（1）由轴对称的性质可得：△EAD≌△EA'D,其中∠EAD=∠EA'D,∠AED=∠A'ED,∠ADE=∠A'DE.
（2）结合（1）的结论，根据平角的定义可得：∠1=180°-2x，∠2=180°-2y；
（3））在△ABC中，∠A+∠B+∠C=180°①；
在△ADE中∠A+∠ADE+∠AED=180°②；
在四边形BCDE中∠B+∠C+∠1+∠2+∠A'DE+∠A'ED=360°③；
①+②-③得，2∠A=∠1+∠2．
点睛：在研究折叠问题时，有全等图形 ( http: / / www.21cnjy.com )出现，要充分利用全等的性质．注意：①几何计算题中，常用到方程的思想；②求角的度数常常要用到“三角形的内角和是180°这一隐含的条件；③三角形的外角通常情况下是转化为内角来解决．21教育网
19．见解析
【解析】试题分析：观察题中图形，从图形中找到关键点向直线引垂线并延长相同长度，找到对应点，顺次连接即可．21*cnjy*com
试题解析：
如图:
( http: / / www.21cnjy.com / )
( http: / / www.21cnjy.com / )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)