5.4 利用轴对称进行设计同步练习

21世纪教育网 –中小学教育资源及组卷应用平台
5.4 利用轴对称进行设计同步练习
　班级__________姓名____________总分___________
本节应掌握和应用的知识点
利用轴对称设计图案应注意以下几点:
(１)要有明确的设计意图．
(２)创意要新颖独特．
(３)设计出的图案要符合要求
基础知识和能力拓展精练
一、选择题
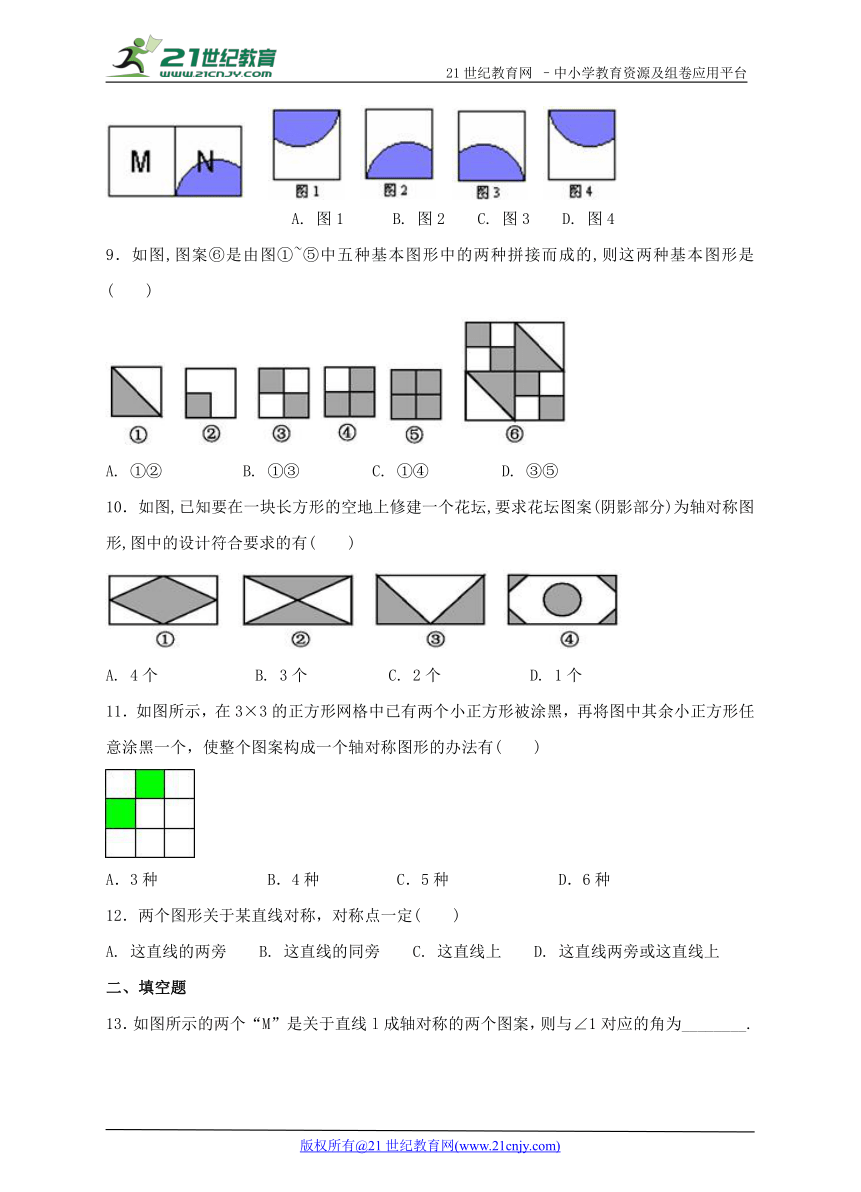
1．桌面上有A、B两球，若要将B球射向桌面任意一边，使一次反弹后击中A，则如图所示8个点中，可以瞄准的点的个数（ ）
A. 1 B. 2 C. 4 D. 6
2．如图，将一个等腰直角三角形按图示方式依次翻折，则下列说法正确的个数有（ ）
①DF平分∠BDE；②△BFD是等腰三角形；③△CED的周长等于BC的长
A. 1个 B. 2个 C. 3个 D. 0个
3．如图，将一正方形纸片沿图（1）、（2）的虚线对折，得到图（3），然后沿图（3）中虚线的剪去一个角，展开得平面图形（4），则图（3）的虚线是（ ）
A． B． C． D．
4．已知∠AOB＝30°，点P在∠AOB的内部，点P1和点P关于OA对称，点P2和点P关于OB对称，则P1、O、P2三点构成的三角形是（ ）
A. 直角三角形 B. 钝角三角形 C. 等腰直角三角形 D. 等边三角形
5．如图，△ABC和△A′B′C′关于直线l对称，下列结论中：①△ABC≌△A′B′C′；
②∠BAC′=∠B′AC；③l垂直平分CC′；④直线BC和B′C′的交点不一定在l上，正确的有（ ）
A. 4个 B. 3个 C. 2个 D. 1个
6．剪纸是中国的民间艺术,剪纸的方法有很多,下面是一种剪纸的方法.如图,先将纸折叠,然后剪出图形,再展开,即可得到图案.
下面四个图案中,不能用上述方法剪出的是(　　)
A. B. C. D.
7．下列图案中，不能用折叠剪纸方法得到的是( ）
A. B. C. D.
8．下列右侧四幅图中，平行移动到位置M后能与N成轴对称的是（ ）
A. 图1 B. 图2 C. 图3 D. 图4
9．如图,图案⑥是由图①~⑤中五种基本图形中的两种拼接而成的,则这两种基本图形是(　　)
A. ①② B. ①③ C. ①④ D. ③⑤
10．如图,已知要在一块长方形的空地上修建一个花坛,要求花坛图案(阴影部分)为轴对称图形,图中的设计符合要求的有(　　)
A. 4个 B. 3个 C. 2个 D. 1个
11．如图所示，在3×3的正方形网格中已有两个小正方形被涂黑，再将图中其余小正方形任意涂黑一个，使整个图案构成一个轴对称图形的办法有(　　)
A．3种 B．4种 C．5种 D．6种
12．两个图形关于某直线对称，对称点一定( )
A. 这直线的两旁 B. 这直线的同旁 C. 这直线上 D. 这直线两旁或这直线上
二、填空题
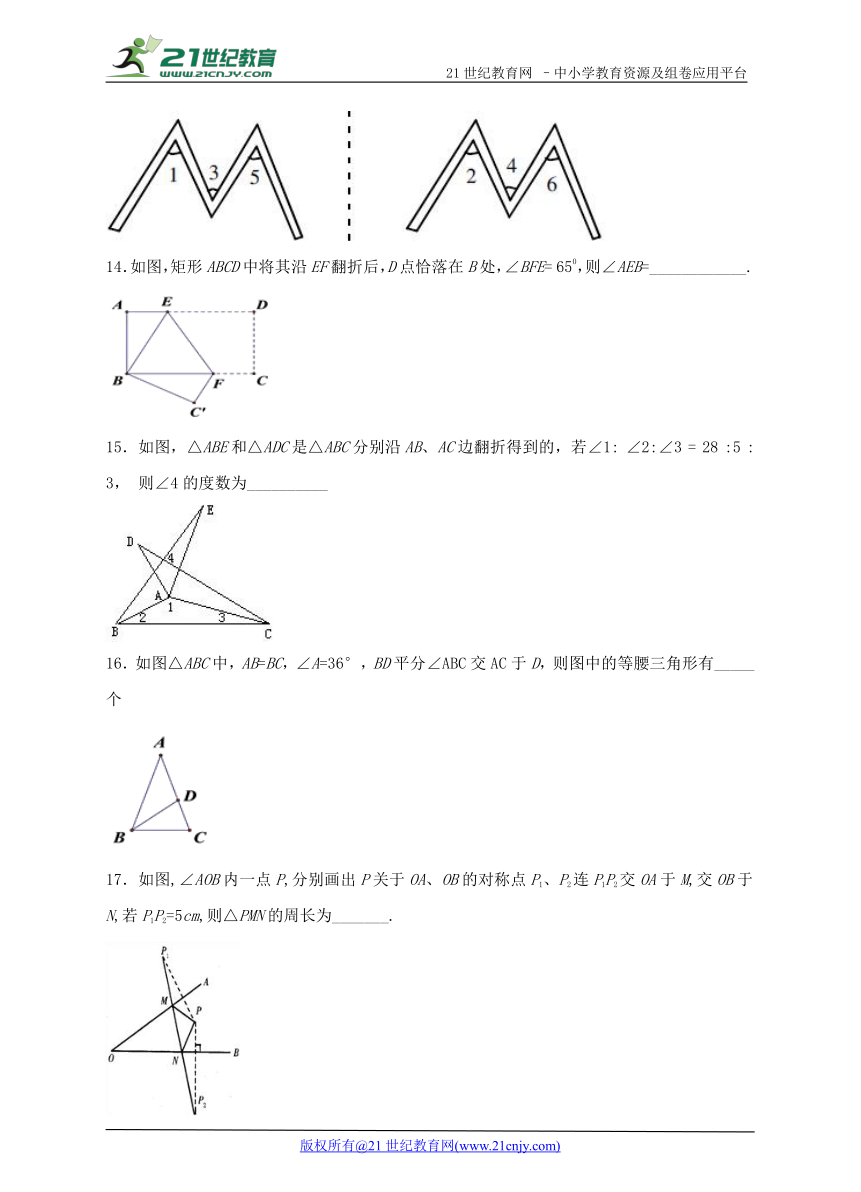
13．如图所示的两个“M”是关于直线l成轴对称的两个图案，则与∠1对应的角为________.
14．如图，矩形ABCD中将其沿EF翻折后，D点恰落在B处，∠BFE= 650，则∠AEB=____________.
15．如图，△ABE和△ADC是△ABC分别沿AB、AC边翻折得到的，若∠1: ∠2:∠3 = 28 :5 : 3， 则∠4的度数为__________
16．如图△ABC中，AB=BC，∠A=36°，BD平分∠ABC交AC于D，则图中的等腰三角形有_____个
17．如图,∠AOB内一点P,分别画出P关于OA、OB的对称点P1、P2连P1P2交OA于M,交OB于N,若P1P2=5cm,则△PMN的周长为_______.
三、解答题
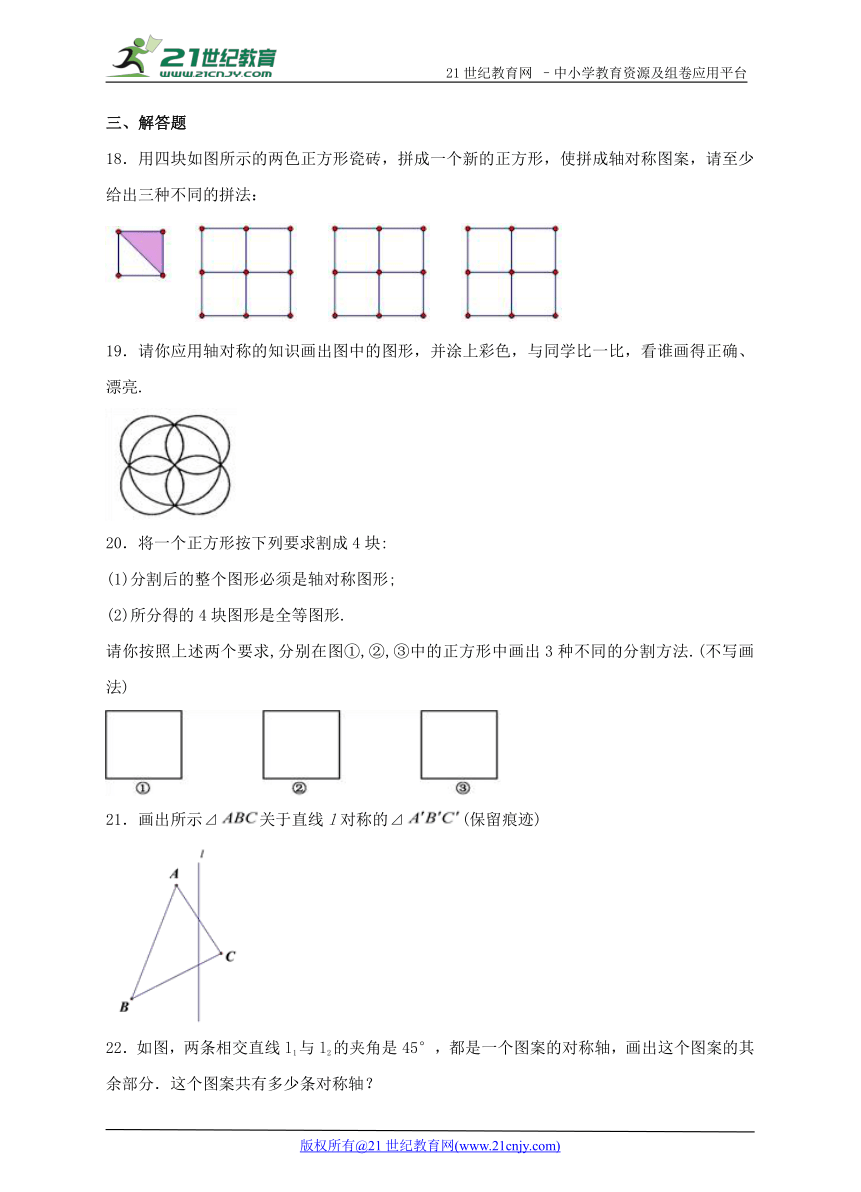
18．用四块如图所示的两色正方形瓷砖，拼成一个新的正方形，使拼成轴对称图案，请至少给出三种不同的拼法：
19．请你应用轴对称的知识画出图中的图形，并涂上彩色，与同学比一比，看谁画得正确、漂亮.
20．将一个正方形按下列要求割成4块:
(1)分割后的整个图形必须是轴对称图形;
(2)所分得的4块图形是全等图形.
请你按照上述两个要求,分别在图①,②,③中的正方形中画出3种不同的分割方法.(不写画法)
21．画出所示⊿关于直线l对称的⊿(保留痕迹)
22．如图，两条相交直线l1与l2的夹角是45°，都是一个图案的对称轴，画出这个图案的其余部分．这个图案共有多少条对称轴？
23．以给出的图形“○○,△△,”(两个圆、两个三角形、两条平行线)为构件,设计一个构思独特且有意义的轴对称图形.举例:如图①是符合要求的一个图形,你还能构思出其他的图形吗 请在图②中画出与之不同的一个图形,并写出一两句贴切的解说词.
24．将△ABC的∠C折起，翻折后角的顶点位置记作C′，当C′落在AC上时（如图1），易证：∠1=2∠2.
当C′点落在CA和CB之间（如图2）时，或当C′落在CB、CA的同旁（如图3）时，∠1、∠2、∠3关系又如何？请写出你的猜想，并就其中一种情况给出证明.
图1 图2 图3
参考答案
1．B
【解析】利用轴对称的性质准确画出图形即可得出答案.
解：要想一次反弹后击中A，需要入射角也反射角相等，因此，可以经过如下图所示的两条路径达到要求，即B-D-A或者B-C-A，另外的一次反弹路线，都不经过图中给出的点，故选B.
点睛：本题关键是正确理解分析出反弹角度与B碰撞边的角度相同.
2．B
【解析】根据轴对称的性质即可得出答案.
解：由多次翻折可得，∠DBE=∠ABD= EMBED Equation.DSMT4 ∠ABC=×45°=22.5°，
∠CDE =90°－∠C =90°－45°=45°=∠C，
∠FDE=∠CDE =45°，
∴∠ABD=∠EDB=∠ADE=×(180°－∠CDE) =×(180°－45°)=67. 5°，
∴①DF平分∠BDE错误，如果正确的话，∠BDE就为90°了；
②△BFD是等腰三角形正确，易得∠BDF=∠∠EDB－∠FDE =22.5°=∠DBE，
③△CED的周长等于BC的长，因为有BC=BF+FE+EC =DF+FE+EC=DC+DE+EC=△CED的周长.
故选B
点睛：本题主要考查了轴对称的性质.解题的关键是正确分析多次翻折后，分清楚各角的大小，以及对应相等的线段.
3．D
【解析】
试题分析：对于此类问题，学生只要亲自动手操作，答案就会很直观地呈现．
解：由于得到的图形的中间是正方形，那么它的四分之一为等腰直角三角形．
故选D．
4．D
【解析】
连接OP，
∵点P1和点P关于OA对称，点P2和点P关于OB对称，
∴OA垂直平分PP1，OB垂直平分PP2，
∴OP=OP1，OP=OP2，
∴OP1=OP2，∠P1OA=∠AOP，∠P2OB=∠BOP，
∵∠AOB=30°，
∴∠P1O P2=∠P1O P+∠P2O P=2∠AOP+2∠BOP=2（∠AOP+∠BOP）=2∠AOB=60°，
∴△P1O P2是等边三角形.
故选D.
点睛：本题关键在于利用图形轴对称变换的性质得出对应的角、边之间的关系，从而判断出△P1O P2的形状.
5．B
【解析】解：∵△ABC和△A′B′C′关于直线l对称，
∴①△ABC≌△A′B′C′，正确；
②∠BAC=∠B′AC′，
∴∠BAC+∠CAC′=∠B′AC′+∠CAC′，
即∠BAC′=∠B′AC正确；
③l垂直平分CC′，正确；
④应为：直线BC和B′C′的交点一定在l上，故本小题错误．
综上所述，结论正确的是①②③共3个．
故选B．
6．C
【解析】将纸对折再对折将会出现两条互相垂直的折痕，剪出的图形是以这两条折痕为对称轴的轴对称图形，图A、图B、图D均能用上述方法剪出．图C是轴对称图形，但只有一条对称轴，所以将纸折叠不会剪出此图形．
故选：C.
7．C
【解析】根据轴对称图形的定义即可解答.
解：由给出的图案，结合轴对称的性质，可知C是旋转一定的角度后与原来的图案对称的，不是一个轴对称图形，故选C.
点睛：本题主要考查轴对称的知识.解题的关键是正确分析出有无对称轴.
8．C
【解析】根据平移的性质即可解答.
解答：要想平行移动到位置M后能与N成轴对称，则一定是以M、N的公共边所在直线为对称轴，故选C.
点睛：本题主要考查图形的平移.解题的关键是正确分析移动后的对称轴在什么位置.
9．B
【解析】根据已知图形，利用分割与组合的原理对图形进行分析即可．
解：如图所示：图案⑥是由图①和图③这两种基本图形拼接而成的.
故选：B.
点睛：本题主要考查对图案设计中的基本图形的识别.解题的关键是要利用分割与组合的原理对图形进行分析.
10．A
【解析】根据轴对称图形的概念即可判定.
解：四副设计图中的阴影部分均为轴对称图形，故满足设计要求的图形有4个.
故选A.
11．C
【解析】
试题分析：如果一个图形沿一条直线对折，直线两旁的部分能互相重合，那么这个图形叫做轴对称图形．
选择一个正方形涂黑，使得3个涂黑的正方形组成轴对称图形，
选择的位置有以下几种：1处，3处，7处，6处，5处，选择的位置共有5处
故选C.
点评：轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
12．D
【解析】由成轴对称的定义知，成轴对称的两个图形的对称点，或者在对称轴上，或者在对称轴两旁.
故选D.
点睛：本题考查了成轴对称的定义，一个图形以某条直线为对称轴，经过轴对称后，能够与另一个图形完全重合，就说这两个图形关于这条直线成轴对称，重合的点叫做对应点.
13．∠6
【解析】试题解析：结合图形可得∠1的对应角为∠6．故应填∠6．
14．50°
【解析】根据翻折求出各个角的度数，再根据平角180°求出∠AEB的度数即可.
解：如图所示，
由矩形ABCD可得AD∥BC，
∴∠1=∠BFE =65°，
由翻折得∠2=∠1 =65°，
∴∠AEB =180°-∠1- ∠2 =180°-65°-65°=50°.
15．80°
【解析】根据翻折求出各个角的度数，再根据三角形的一个外角等于和它不相邻的两个内角的和求出∠4的度数.
解：∵∠1: ∠2:∠3 = 28 :5 : 3，
∠1+∠2+∠3 = 180°，
∴∠1=140°，∠2=25°，∠3=15°，
由翻折得∠EBA =∠2 =25°，∠DCA =∠3 =15°，
∴∠EBC=∠EBA +∠2 =50°，∠DCB =∠DCA +∠3 =30°，
∵三角形的一个外角等于和它不相邻的两个内角的和，
∴∠4=∠EBC +∠DCB =50°+30°=80°.
16．3
【解析】根据条件求出各个角的度数，由此确定哪个三角形是等腰三角形
解答：∵在△ABC中，AB=BC，∠A=36°，
∴∠ABC=∠ACB =72°，
∵BD平分∠ABC，
∴∠ABD=∠CBD =36°，
∴∠ABD=∠A =36°，∠BDC =72°=∠C，
∴△ABD和△BDC都是等腰三角形.
故有三个等腰三角形 故有三个.
点睛：本题主要考查了等腰三角形的判定.利用已知条件求出等角是判断等腰三角形的关键.
17．5cm
【解析】∵P、P1,P、P2关于OA、OB对称，
∴PM=P1M,PN=P2N，
∴△PMN的周长=P1P2，
∴△PMN的周长是5 cm.
点睛：本题考查了轴对称的性质和线段垂直平分线的性质，成轴对称的两个图形中，对应点的连线被对称轴垂直平分；线段垂直平分线上的点到线段两个端点的距离相等.
18．见解析
【解析】根据轴对称的概念进行图形设计即可.
解：根据轴对称要求，设计出利用两色磁砖拼成的正方形如图所示.
点睛：本题主要考查了利用轴对称进行设计方案.解题的关键是确定以哪条直线为对称轴，然后在确定两色磁砖的摆放位置.
19．见解析
【解析】根据轴对称的知识进行图形设计即可.
解：如图所示：
1.作一个正方形ABCD；
2.分别以正方形ABCD的四条边为直径，作四个圆；
3.以这四个圆的公共点为圆心O，OA长为半径作一个圆.
4.将线段与字母去掉.
就得到图中第二个图形.
然后按轴对称的要求涂色.
点睛：本题考查了轴对称知识.解题的关键是找出各个圆的圆心位置.
20．答案不唯一,
【解析】分割后的整个图形必须是轴对称图形，作两边的中垂线；四块图形的完全相同，作法较多，符合要求即可．
解：如图所示.
21．见解析
【解析】根据画轴对称图形的方法即可得出答案.
作法：如图所示，
1.作点△的三个顶点A、B、C关于直线l对称的点A’、B’、C’；
2.顺次连结A’B’、 B’ C’、C’ A’得⊿A’B’C.
则△A’B’C即为所求作的三角形.
22．答案见解析.
【解析】试题分析：根据轴对称图形和对称轴的定义即可得到结果.
如图所示：
这个图案共有四条对称轴.
点评：解答本题的关键是熟练掌握轴对称图形的定义：如果把一个图形沿一条直线对折，直线两旁的部分能够完全重合，那么这个图形就叫做轴对称图形，这条直线叫对称轴.
23．能;
【解析】利用轴对称进行设计图案即可.
解：如图所示.
解说词：两人相伴.
24．见解析
【解析】利用轴对称的知识找出等解即可进行推理判断.
解：当C′点落在CA和CB之间（如图2）时，∠1+∠3=2∠2；
当C′落在CB、CA的同旁（如图3）时，∠1－∠3=2∠2；
对于图2证明如下：
连结CC’，如图4所示，
∵⊿EC’D是由⊿ECD翻折得到的，
∴⊿EC’D≌⊿ECD，由此得EC=EC’，DC=DC’，∠EC’D=∠ECD，
∴∠EC’C=∠ECC；∠DC’C=∠DCC，
∵∠1=∠DC’C+∠DCC’ ，∠3=∠EC’C+∠ECC’ ，
∴∠1+∠3=∠DC’C+∠DCC’ +∠ EC’C+∠ECC’=2∠DC’C+2∠ EC’C =2(∠DC’C+∠ EC’C)= 2∠2；
∴∠1+∠3=2∠2；
对于图3证明如下：
设AC与DC’在⊿ABC内部所夹角为∠4，如图5所示，
则有∠1=∠C+∠4，∠4=∠3+∠2，
又由翻折得：∠2=∠C，
∴∠1=∠2+∠3+∠2=∠3+2∠2，
∴∠1－∠3=2∠2.
点睛：本题主要考查了轴对称的性质.找准对称轴是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)