人教版初中数学八年级下册19.1变量与函数同步练习题(含答案)
文档属性
| 名称 | 人教版初中数学八年级下册19.1变量与函数同步练习题(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 78.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-05 16:10:55 | ||
图片预览


文档简介
《19.1函数》同步练习题
一、选择题(每小题只有一个正确答案)
1.某型号的汽车在路面上的制动距离s=,其中变量是( )
A. s,v B. s,v2 C. s D. v
2.函数y=中,自变量x的取值范围是( )
A. x≥﹣1 B. x>2 C. x>﹣1且x≠2 D. x≥﹣1且x≠2
3.关于变量x,y有如下关系:①x﹣y=5;②y2=2x;③:y=|x|;④y=3x-1.其中y是x函数的是( )21世纪教育网版权所有
A. ①②③ B. ①②③④ C. ①③ D. ①③④
4.图中,表示y是x的函数图象是( )
5.甲、乙、丙三车从A城出发匀速前往B城.在整个行程中,汽车离开A城的距离s与时刻t的对应关系如下图所示.那么8:00时,距A城最远的汽车是21教育网
A. 甲车 B. 乙车
C. 丙车 D. 甲车和乙车
6.已知两个变量x和y,它们之间的3组对应值如下表所示:
x
-1
0
1
y
-1
1
3
则y与x之间的函数关系式可能是( )
A. y=x B. y=2x+1 C. y=x2+x+1 D. y=3x
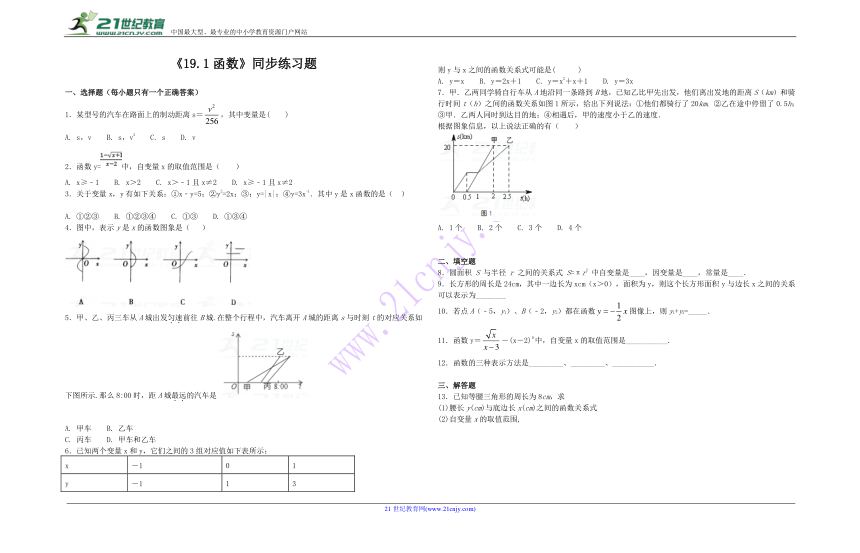
7.甲.乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离S(km)和骑行时间t(h)之间的函数关系如图1所示,给出下列说法:①他们都骑行了20km;②乙在途中停留了0.5h;③甲.乙两人同时到达目的地;④相遇后,甲的速度小于乙的速度.21cnjy.com
根据图象信息,以上说法正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
二、填空题
8.圆面积 S 与半径 r 之间的关系式 S=πr2 中自变量是____,因变量是____,常量是____.
9.长方形的周长是24cm,其中一边长为xcm(x>0),面积为y,则这个长方形面积y与边长x之间的关系可以表示为________21·cn·jy·com
10.若点A(﹣5,y1)、B(﹣2,y2)都在函数图像上,则y1+y2=_____.
11.函数y=-(x-2)0中,自变量x的取值范围是___________.
12.函数的三种表示方法是_________、_________、___________.
三、解答题
13.已知等腰三角形的周长为8cm,求
(1)腰长y(cm)与底边长x(cm)之间的函数关系式
(2)自变量x的取值范围,
14.小凡与小光从学校出发到距学校5千米的图书馆看书,小光直接去图书馆, 小凡途中从路边超市买了一些学习用品,如图反应了他们俩人离开学校的路程s(千米)与时间t(分钟)的关系,请根据图象提供的信息回答问题:www.21-cn-jy.com
(1) 是描述小凡的运动过程(填或);
(2)小凡和小光先出发的是 ,先出发了 分钟;
(3)小凡与小光先到达图书馆的是 ,先到了 分钟;
(4)求小凡与小光从学校到图书馆的平均速度各是多少?(不包括中间停留的时间)
15.某厂按用户的月需求量x(件)完成一种产品的生产,其中x>0.每件的售价为18万元,每件的成本y(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量x(件)成反比.经市场调研发现,月需求量x与月份n(n为整数,1≤n≤12)符合关系式x=2n2﹣2kn+9(k+3)(k为常数),且得到了表中的数据2·1·c·n·j·y
月份n(月)1
1
2
成本y(万元/件)
11
12
需求量x(件/月)
120
100
(1)直接写出k的值;
(2)求y与x满足的关系式,请说明一件产品的利润能否是12万元;
(3)推断是否存在某个月既无盈利也不亏损.
参考答案
1.A
【解析】∵汽车在路面上的制动距离s=,
∴S随着V的变化而变化,
∴变量是S、V,
故选A.
2.D
【解析】解:根据题意得:,解得:x≥﹣1且x≠2.故选D.
3.D
【解析】试题解析:y是x函数的是①x-y=5;③:y=|x|;④y=3x-1.
当x=1时,在y2=2x中y=±,则不是函数;
故选D.
4.C
【解析】试题解析:A.对于x的每一个取值,y不是都有唯一确定的值与之对应,y不是x的函数,故A选项不符合题意;
B.对于x的每一个取值,y不是都有唯一确定的值与之对应,y不是x的函数,故B选项不符合题意;
C.对于x的每一个取值,y都有唯一确定的值与之对应,y是x的函数,故C选项符合题意;
D.对于x的每一个取值,y不是都有唯一确定的值与之对应,y不是x的函数,故B选项不符合题意.
故选C.
5.B
【解析】试题解析:8:00时,距A城最远的汽车是乙车,
故选B.
6.B
【解析】A.将表格对应数据代入,不符合方程y=x,故A错误;
B.将表格对应数据代入,符合方程y=2x+1,故B正确;
C.将表格对应数据代入,不符合方程y=x2+x+1,故C错误;
D.将表格对应数据代入,不符合方程y=3x,故D错误.
故选:B.
7.B
【解析】由图象知甲乙最后的路程都是20km,所以说法①是正确的;乙在0.5-1h这段时间里,路程没有变化,所以可以说乙在途中停留了0.5h,故②正确;甲在第2h时行驶了20km,乙在第2.5h时行驶了20km,故甲比乙先到达目的地,所以③错误;看速度大小就看直线的倾斜率,越陡速度越大,故相遇后甲的速度大些,所以④错误,
综上所述,正确的只有①②两个,
故选B.
8. r S π
【解析】解:S=πr2中,自变量为:r,因变量为:S,常量为:π.故答案为:r,s,π.
9.y=(12﹣x)x
【解析】另一边为(24-2x)÷2=12-x,所以长方形面积y与边长x之间的关系可以表示为y=(12﹣x)x,故答案为y=(12﹣x)x.
10.
【解析】因为y1==,y2==,所以y1+y2=+1=,故答案为.
11.x≥0_且x≠2且x≠3_
【解析】根据题意得,x≥0且x-3≠0且x-2≠0,解得x≥0且x≠3且x≠2.故答案为:x≥0且x≠3且x≠2.
12. 图象法 列表法 解析式法
【解析】函数有三种表示方法——图象法、列表法、解析式法,
故答案为:图象法、列表法、解析式法.
13.(1)y=4-0.5x;(2)0【解析】整体分析:
(1)由周长为8可得y与x之间的函数关系式;(2)根据三角形的三边关系和x>0可得x的取值范围.
解:(1)因为2y+x=8,所以y=4-0.5x;
所以腰长y(cm)与底边长x(cm)之间的函数关系式是y=4-0.5x;
(2)由三角形的三边关系得:
y+y>x,即8-x>x,
解得x<4,
又因为x>0,
所以0<x<4.
所以自变量x的取值范围是0<x<4.
14.(1) ;(2)小凡,10;(3)小光,10;(4)小凡的速度是10km/h,小光的速度是7.5km/h.
【解析】试题分析:(1)根据小凡在中途停留一段时间,结合函数图象即可得出结论;
(2)观察函数图象的t(时间)轴,根据出发时间不同即可得出结论;
(3)当s=5千米时,将两函数对应的t(时间)做差,即可得出结论;
(4)根据“速度=路程÷时间”结合两函数图象,即可求出小凡与小光的速度.
试题解析:(1)l1是描述小凡的运动过程的,因为小凡在途中从路边超市买了一些学习用品,需要停留一段时间,此时间段小凡距学校的路程没有变化,所以l1描述了小凡的运动过程,
故答案为:l1;
(2)观察函数图象,发现,小凡先出发,比小光先出发了10分钟,
故答案为:小凡,10;
(3)60-50=10(分钟),
所以小光先到达图书馆,比小凡先到了10分钟,
故答案为:小光,10;
(4)小凡的平均速度为:5÷=10(km/h),
小光的平均速度为:5÷=7.5(km/h),
答:小凡从学校到图书馆的平均速度是10km/h,小光从学校到图书馆的平均速度是7.5km/h.
15.(1)k=13;(2)一件产品的利润不可能是12万元;(3)不存在某个月既无盈利也不亏损.
【解析】试题分析:(1)根据已知月份与x的值,取一组需求量x与月份n代入x=2n2﹣2kn+9(k+3)即可求出k;
(2)根据题意得y=a+,由表中数据列方程组求解,即可得到y与x的关系式;
(3)根据不亏损也不盈利列方程求出x的值,进行解答;
解:(1)将n=1,x=120代入x=2n2-2kn+9(k+3),
得2×12-2k+9(k+3)=120,
解得k=13,
(2)设基础价为a,则根据题意可得y=a+,根据表格可得
,
解得,
∴y=6+.
利润为12万元时,成本价为6万元,则=0,
∵>0,则一件产品的利润不能是12万元;
(3)当n=2,x=100时也满足
当不盈利也不亏损时,成本价为18万元,
则6+600x=18,
解得x=50,
则50=2n2-26n+144,
即n2-13n+47=0.
方程根的判别式△=(-13)2-4×1×47<0,故方程无实根,
则不存在某个月既无盈利也不亏损.
一、选择题(每小题只有一个正确答案)
1.某型号的汽车在路面上的制动距离s=,其中变量是( )
A. s,v B. s,v2 C. s D. v
2.函数y=中,自变量x的取值范围是( )
A. x≥﹣1 B. x>2 C. x>﹣1且x≠2 D. x≥﹣1且x≠2
3.关于变量x,y有如下关系:①x﹣y=5;②y2=2x;③:y=|x|;④y=3x-1.其中y是x函数的是( )21世纪教育网版权所有
A. ①②③ B. ①②③④ C. ①③ D. ①③④
4.图中,表示y是x的函数图象是( )
5.甲、乙、丙三车从A城出发匀速前往B城.在整个行程中,汽车离开A城的距离s与时刻t的对应关系如下图所示.那么8:00时,距A城最远的汽车是21教育网
A. 甲车 B. 乙车
C. 丙车 D. 甲车和乙车
6.已知两个变量x和y,它们之间的3组对应值如下表所示:
x
-1
0
1
y
-1
1
3
则y与x之间的函数关系式可能是( )
A. y=x B. y=2x+1 C. y=x2+x+1 D. y=3x
7.甲.乙两同学骑自行车从A地沿同一条路到B地,已知乙比甲先出发,他们离出发地的距离S(km)和骑行时间t(h)之间的函数关系如图1所示,给出下列说法:①他们都骑行了20km;②乙在途中停留了0.5h;③甲.乙两人同时到达目的地;④相遇后,甲的速度小于乙的速度.21cnjy.com
根据图象信息,以上说法正确的有( )
A. 1个 B. 2个 C. 3个 D. 4个
二、填空题
8.圆面积 S 与半径 r 之间的关系式 S=πr2 中自变量是____,因变量是____,常量是____.
9.长方形的周长是24cm,其中一边长为xcm(x>0),面积为y,则这个长方形面积y与边长x之间的关系可以表示为________21·cn·jy·com
10.若点A(﹣5,y1)、B(﹣2,y2)都在函数图像上,则y1+y2=_____.
11.函数y=-(x-2)0中,自变量x的取值范围是___________.
12.函数的三种表示方法是_________、_________、___________.
三、解答题
13.已知等腰三角形的周长为8cm,求
(1)腰长y(cm)与底边长x(cm)之间的函数关系式
(2)自变量x的取值范围,
14.小凡与小光从学校出发到距学校5千米的图书馆看书,小光直接去图书馆, 小凡途中从路边超市买了一些学习用品,如图反应了他们俩人离开学校的路程s(千米)与时间t(分钟)的关系,请根据图象提供的信息回答问题:www.21-cn-jy.com
(1) 是描述小凡的运动过程(填或);
(2)小凡和小光先出发的是 ,先出发了 分钟;
(3)小凡与小光先到达图书馆的是 ,先到了 分钟;
(4)求小凡与小光从学校到图书馆的平均速度各是多少?(不包括中间停留的时间)
15.某厂按用户的月需求量x(件)完成一种产品的生产,其中x>0.每件的售价为18万元,每件的成本y(万元)是基础价与浮动价的和,其中基础价保持不变,浮动价与月需求量x(件)成反比.经市场调研发现,月需求量x与月份n(n为整数,1≤n≤12)符合关系式x=2n2﹣2kn+9(k+3)(k为常数),且得到了表中的数据2·1·c·n·j·y
月份n(月)1
1
2
成本y(万元/件)
11
12
需求量x(件/月)
120
100
(1)直接写出k的值;
(2)求y与x满足的关系式,请说明一件产品的利润能否是12万元;
(3)推断是否存在某个月既无盈利也不亏损.
参考答案
1.A
【解析】∵汽车在路面上的制动距离s=,
∴S随着V的变化而变化,
∴变量是S、V,
故选A.
2.D
【解析】解:根据题意得:,解得:x≥﹣1且x≠2.故选D.
3.D
【解析】试题解析:y是x函数的是①x-y=5;③:y=|x|;④y=3x-1.
当x=1时,在y2=2x中y=±,则不是函数;
故选D.
4.C
【解析】试题解析:A.对于x的每一个取值,y不是都有唯一确定的值与之对应,y不是x的函数,故A选项不符合题意;
B.对于x的每一个取值,y不是都有唯一确定的值与之对应,y不是x的函数,故B选项不符合题意;
C.对于x的每一个取值,y都有唯一确定的值与之对应,y是x的函数,故C选项符合题意;
D.对于x的每一个取值,y不是都有唯一确定的值与之对应,y不是x的函数,故B选项不符合题意.
故选C.
5.B
【解析】试题解析:8:00时,距A城最远的汽车是乙车,
故选B.
6.B
【解析】A.将表格对应数据代入,不符合方程y=x,故A错误;
B.将表格对应数据代入,符合方程y=2x+1,故B正确;
C.将表格对应数据代入,不符合方程y=x2+x+1,故C错误;
D.将表格对应数据代入,不符合方程y=3x,故D错误.
故选:B.
7.B
【解析】由图象知甲乙最后的路程都是20km,所以说法①是正确的;乙在0.5-1h这段时间里,路程没有变化,所以可以说乙在途中停留了0.5h,故②正确;甲在第2h时行驶了20km,乙在第2.5h时行驶了20km,故甲比乙先到达目的地,所以③错误;看速度大小就看直线的倾斜率,越陡速度越大,故相遇后甲的速度大些,所以④错误,
综上所述,正确的只有①②两个,
故选B.
8. r S π
【解析】解:S=πr2中,自变量为:r,因变量为:S,常量为:π.故答案为:r,s,π.
9.y=(12﹣x)x
【解析】另一边为(24-2x)÷2=12-x,所以长方形面积y与边长x之间的关系可以表示为y=(12﹣x)x,故答案为y=(12﹣x)x.
10.
【解析】因为y1==,y2==,所以y1+y2=+1=,故答案为.
11.x≥0_且x≠2且x≠3_
【解析】根据题意得,x≥0且x-3≠0且x-2≠0,解得x≥0且x≠3且x≠2.故答案为:x≥0且x≠3且x≠2.
12. 图象法 列表法 解析式法
【解析】函数有三种表示方法——图象法、列表法、解析式法,
故答案为:图象法、列表法、解析式法.
13.(1)y=4-0.5x;(2)0
(1)由周长为8可得y与x之间的函数关系式;(2)根据三角形的三边关系和x>0可得x的取值范围.
解:(1)因为2y+x=8,所以y=4-0.5x;
所以腰长y(cm)与底边长x(cm)之间的函数关系式是y=4-0.5x;
(2)由三角形的三边关系得:
y+y>x,即8-x>x,
解得x<4,
又因为x>0,
所以0<x<4.
所以自变量x的取值范围是0<x<4.
14.(1) ;(2)小凡,10;(3)小光,10;(4)小凡的速度是10km/h,小光的速度是7.5km/h.
【解析】试题分析:(1)根据小凡在中途停留一段时间,结合函数图象即可得出结论;
(2)观察函数图象的t(时间)轴,根据出发时间不同即可得出结论;
(3)当s=5千米时,将两函数对应的t(时间)做差,即可得出结论;
(4)根据“速度=路程÷时间”结合两函数图象,即可求出小凡与小光的速度.
试题解析:(1)l1是描述小凡的运动过程的,因为小凡在途中从路边超市买了一些学习用品,需要停留一段时间,此时间段小凡距学校的路程没有变化,所以l1描述了小凡的运动过程,
故答案为:l1;
(2)观察函数图象,发现,小凡先出发,比小光先出发了10分钟,
故答案为:小凡,10;
(3)60-50=10(分钟),
所以小光先到达图书馆,比小凡先到了10分钟,
故答案为:小光,10;
(4)小凡的平均速度为:5÷=10(km/h),
小光的平均速度为:5÷=7.5(km/h),
答:小凡从学校到图书馆的平均速度是10km/h,小光从学校到图书馆的平均速度是7.5km/h.
15.(1)k=13;(2)一件产品的利润不可能是12万元;(3)不存在某个月既无盈利也不亏损.
【解析】试题分析:(1)根据已知月份与x的值,取一组需求量x与月份n代入x=2n2﹣2kn+9(k+3)即可求出k;
(2)根据题意得y=a+,由表中数据列方程组求解,即可得到y与x的关系式;
(3)根据不亏损也不盈利列方程求出x的值,进行解答;
解:(1)将n=1,x=120代入x=2n2-2kn+9(k+3),
得2×12-2k+9(k+3)=120,
解得k=13,
(2)设基础价为a,则根据题意可得y=a+,根据表格可得
,
解得,
∴y=6+.
利润为12万元时,成本价为6万元,则=0,
∵>0,则一件产品的利润不能是12万元;
(3)当n=2,x=100时也满足
当不盈利也不亏损时,成本价为18万元,
则6+600x=18,
解得x=50,
则50=2n2-26n+144,
即n2-13n+47=0.
方程根的判别式△=(-13)2-4×1×47<0,故方程无实根,
则不存在某个月既无盈利也不亏损.
