8.3 实际问题与二元一次方程组的应用课件
文档属性
| 名称 | 8.3 实际问题与二元一次方程组的应用课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 497.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-06 10:42:03 | ||
图片预览






文档简介
(共17张PPT)
寻找“等量关系”
人教课标版 七年级下
问题导入
例1.张大叔承包的10亩地理所种植的甲、乙两种蔬菜共获利13800元,其中甲种蔬菜每亩获利1200元,乙种蔬菜每亩获利1500元.问甲、乙两种蔬菜各种植了多少亩?
试着标注题目中等量关系
新知讲解
分析:题目中的等量关系非常明显:甲乙两种蔬菜共种植10亩;甲乙两种蔬菜共获利13800元。由这两个等量关系列出方程组求解即可。
解:设甲、乙两种蔬菜的面积分别为x亩、y亩,依题意得
X+y=10
1200x+1500y=13800
解得 x=4
y=6
答:甲种蔬菜种植了4亩,乙种蔬菜种植了6亩
方法小结
在理解题意基础上,挑出关键语句、数量关系用整式依次表示出来,根据“同一量”的不同表达形式,找到相等关系。
译式法
和倍问题
牛刀小试
在理解题意基础上,挑出关键语句、数量关系用整式依次表示出来,根据“同一量”的不同表达形式,找到相等关系。
有大小两种货车,2辆大货车与3辆小货车一次可以运货15.5t,5辆大货车与6辆小货车一次可以运货35t.3辆大货车与5辆小货车一次可以运货多少吨?
请快速说出等量关系,并设出未知数写出方程组
行程问题
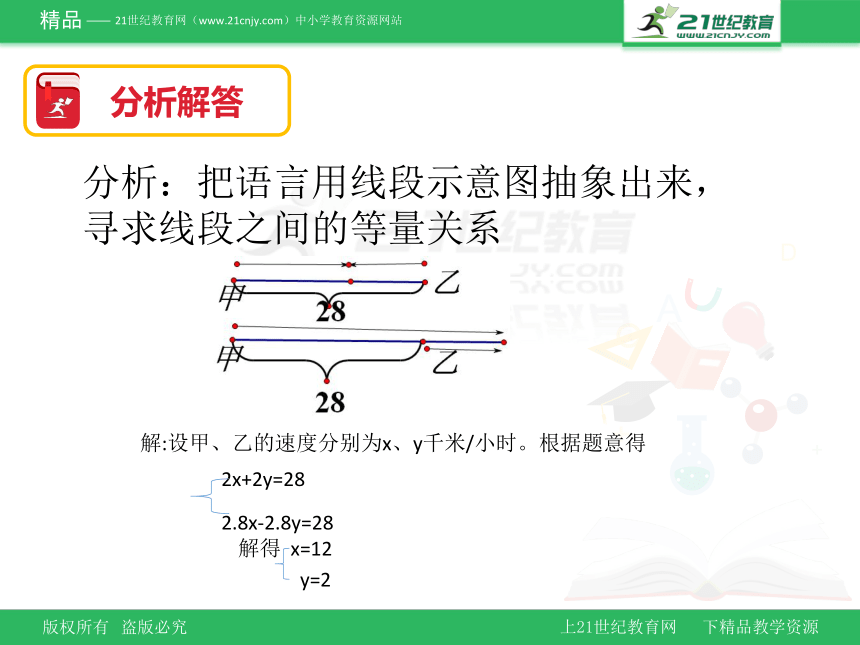
例2.若甲、乙两人同时从相距28千米的两地相向而行,则经过2小时两人相遇。若甲乙两人同时从相距28千米的两地同向出发,则2.8小时后甲能追上乙。求甲、乙两人的速度?
你能从语言中快速找到等量关系吗?
分析解答
分析:把语言用线段示意图抽象出来,寻求线段之间的等量关系
解:设甲、乙的速度分别为x、y千米/小时。根据题意得
2x+2y=28
2.8x-2.8y=28
解得 x=12
y=2
方法小结
将题目中的条件及关系用简单明了的示意图表示出来,根据图中有关数量的内在联系,找到相等关系。
图示法
行程问题
巩固练习
将题目中的条件及关系用简单明了的示意图表示出来,根据图中有关数量的内在联系,找到相等关系。
从甲地到乙地有一段上坡与一段平路。如果保持上坡每小时走3km,平路每小时走4km,下坡每小时走5km,那么从甲地到乙地需54min,从乙地到甲地需42min.甲地到乙地全程是多少?
请快速画出示意图,找出等量关系
解答展示
从甲地到乙地有一段上坡与一段平路。如果保持上坡每小时走3km,平路每小时走4km,下坡每小时走5km,那么从甲地到乙地需54min,从乙地到甲地需42min.甲地到乙地全程是多少?
解:设上坡路段有xkm,平路有ykm,依题意可得
X=1.5
Y=1.6
全程为3.1km
数字问题
例3.两个两位数的和是68.在较大的两位数的右边写上较小的两位数,得到一个四位数;在较大两位数的左边写上较小的两位数,也得到一个四位数。已知前一个四位数比后一个四位数大2178,求这两个两位数。
题目中有哪些等量关系呢?
分析解答
设较大的两位数为x,较小的两位数为y,根据题目中的条件将相关量填入表格中,由表格横向(纵向)找到等量关系。
较大的数 较小的数 关系
两位数 x y 68
四位数 100x+y 100y+x 2178
解:设较大的两位数为x,较小的两位数为y,根据题意得
X+y=68
(100x+y)-(100y+x)=2178
解得 x=45
Y=23
方法小结
将题目中的有关数量及其关系填在事先设计好的表格内,根据表格逐层分析,找到等量关系。
列表法
数字问题,较复杂问题
练习巩固
用一些长短相同的小木棍按图所式,连续摆正方形或六边形要求每两个相邻的图形只有一条公共边。已知摆放的正方形比六边形多4个,并且一共用了110个小木棍,问连续摆放了正方形和六边形各多少个?
…
…
表格浮现等量关系
…
…
图形 连续摆放的个数 (单位:个) 使用小木棒的根数 (单位:根)
正方形 x 4+3(x-1)=3x+1
六边形 y 6+5(y-1)=5y+1
关系 正反方形比六边形多 4 个 共用了 110 根小木棍
课堂小结
寻找等量关系的常规三法
译式法
图示法
表格法
谢谢
寻找“等量关系”
人教课标版 七年级下
问题导入
例1.张大叔承包的10亩地理所种植的甲、乙两种蔬菜共获利13800元,其中甲种蔬菜每亩获利1200元,乙种蔬菜每亩获利1500元.问甲、乙两种蔬菜各种植了多少亩?
试着标注题目中等量关系
新知讲解
分析:题目中的等量关系非常明显:甲乙两种蔬菜共种植10亩;甲乙两种蔬菜共获利13800元。由这两个等量关系列出方程组求解即可。
解:设甲、乙两种蔬菜的面积分别为x亩、y亩,依题意得
X+y=10
1200x+1500y=13800
解得 x=4
y=6
答:甲种蔬菜种植了4亩,乙种蔬菜种植了6亩
方法小结
在理解题意基础上,挑出关键语句、数量关系用整式依次表示出来,根据“同一量”的不同表达形式,找到相等关系。
译式法
和倍问题
牛刀小试
在理解题意基础上,挑出关键语句、数量关系用整式依次表示出来,根据“同一量”的不同表达形式,找到相等关系。
有大小两种货车,2辆大货车与3辆小货车一次可以运货15.5t,5辆大货车与6辆小货车一次可以运货35t.3辆大货车与5辆小货车一次可以运货多少吨?
请快速说出等量关系,并设出未知数写出方程组
行程问题
例2.若甲、乙两人同时从相距28千米的两地相向而行,则经过2小时两人相遇。若甲乙两人同时从相距28千米的两地同向出发,则2.8小时后甲能追上乙。求甲、乙两人的速度?
你能从语言中快速找到等量关系吗?
分析解答
分析:把语言用线段示意图抽象出来,寻求线段之间的等量关系
解:设甲、乙的速度分别为x、y千米/小时。根据题意得
2x+2y=28
2.8x-2.8y=28
解得 x=12
y=2
方法小结
将题目中的条件及关系用简单明了的示意图表示出来,根据图中有关数量的内在联系,找到相等关系。
图示法
行程问题
巩固练习
将题目中的条件及关系用简单明了的示意图表示出来,根据图中有关数量的内在联系,找到相等关系。
从甲地到乙地有一段上坡与一段平路。如果保持上坡每小时走3km,平路每小时走4km,下坡每小时走5km,那么从甲地到乙地需54min,从乙地到甲地需42min.甲地到乙地全程是多少?
请快速画出示意图,找出等量关系
解答展示
从甲地到乙地有一段上坡与一段平路。如果保持上坡每小时走3km,平路每小时走4km,下坡每小时走5km,那么从甲地到乙地需54min,从乙地到甲地需42min.甲地到乙地全程是多少?
解:设上坡路段有xkm,平路有ykm,依题意可得
X=1.5
Y=1.6
全程为3.1km
数字问题
例3.两个两位数的和是68.在较大的两位数的右边写上较小的两位数,得到一个四位数;在较大两位数的左边写上较小的两位数,也得到一个四位数。已知前一个四位数比后一个四位数大2178,求这两个两位数。
题目中有哪些等量关系呢?
分析解答
设较大的两位数为x,较小的两位数为y,根据题目中的条件将相关量填入表格中,由表格横向(纵向)找到等量关系。
较大的数 较小的数 关系
两位数 x y 68
四位数 100x+y 100y+x 2178
解:设较大的两位数为x,较小的两位数为y,根据题意得
X+y=68
(100x+y)-(100y+x)=2178
解得 x=45
Y=23
方法小结
将题目中的有关数量及其关系填在事先设计好的表格内,根据表格逐层分析,找到等量关系。
列表法
数字问题,较复杂问题
练习巩固
用一些长短相同的小木棍按图所式,连续摆正方形或六边形要求每两个相邻的图形只有一条公共边。已知摆放的正方形比六边形多4个,并且一共用了110个小木棍,问连续摆放了正方形和六边形各多少个?
…
…
表格浮现等量关系
…
…
图形 连续摆放的个数 (单位:个) 使用小木棒的根数 (单位:根)
正方形 x 4+3(x-1)=3x+1
六边形 y 6+5(y-1)=5y+1
关系 正反方形比六边形多 4 个 共用了 110 根小木棍
课堂小结
寻找等量关系的常规三法
译式法
图示法
表格法
谢谢
