2018春人教版数学七年级下册7.1.2平面直角坐标系课件
文档属性
| 名称 | 2018春人教版数学七年级下册7.1.2平面直角坐标系课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-06 20:11:10 | ||
图片预览





文档简介
课件21张PPT。7.1.2 平面直角坐标系(2)第七章 平面直角坐标系1、什么是平面直角坐标系?
2、如何由点求坐标?
3、如何由坐标描点?
4、各个象限内点的坐标符号特征是什么?
5、坐标轴上点的坐标特征是什么?
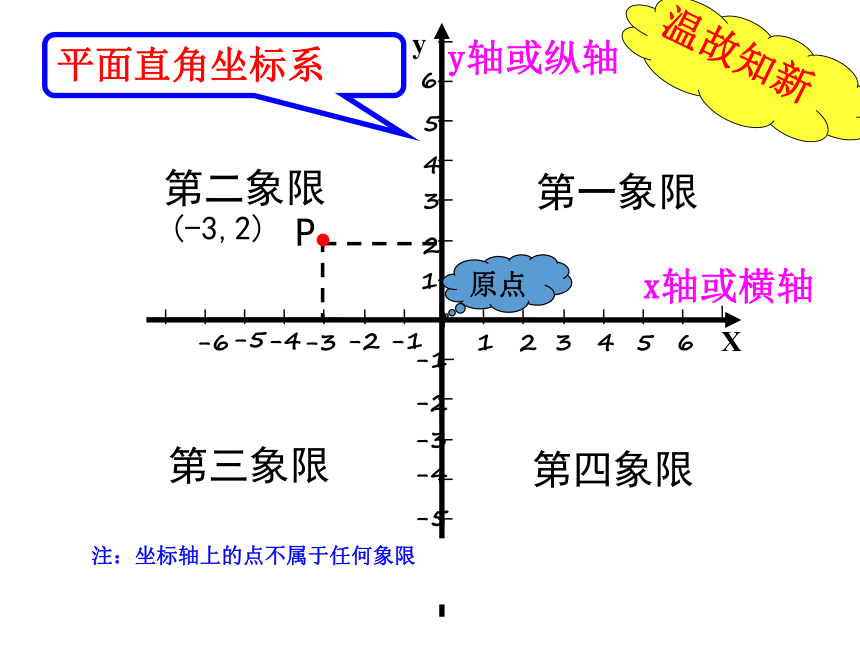
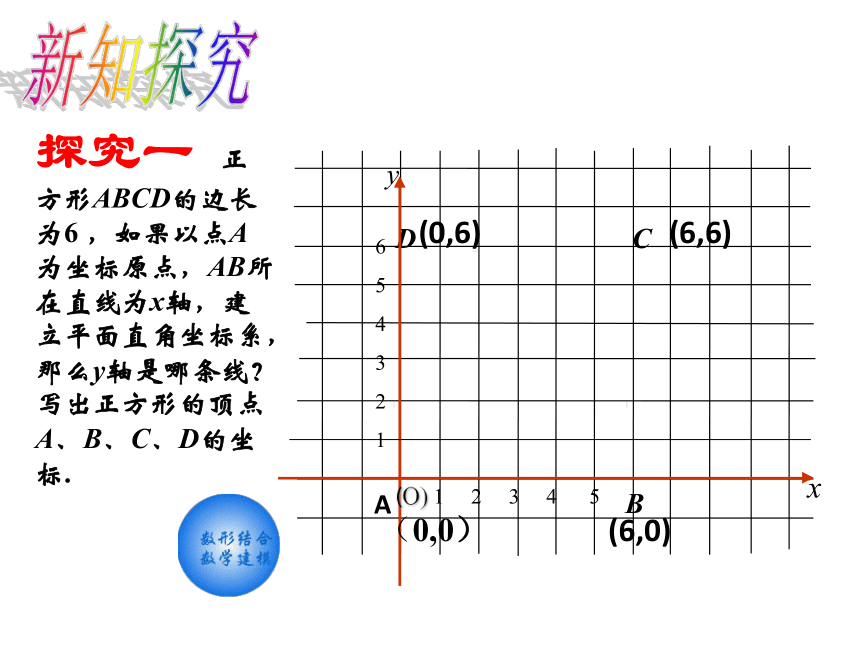
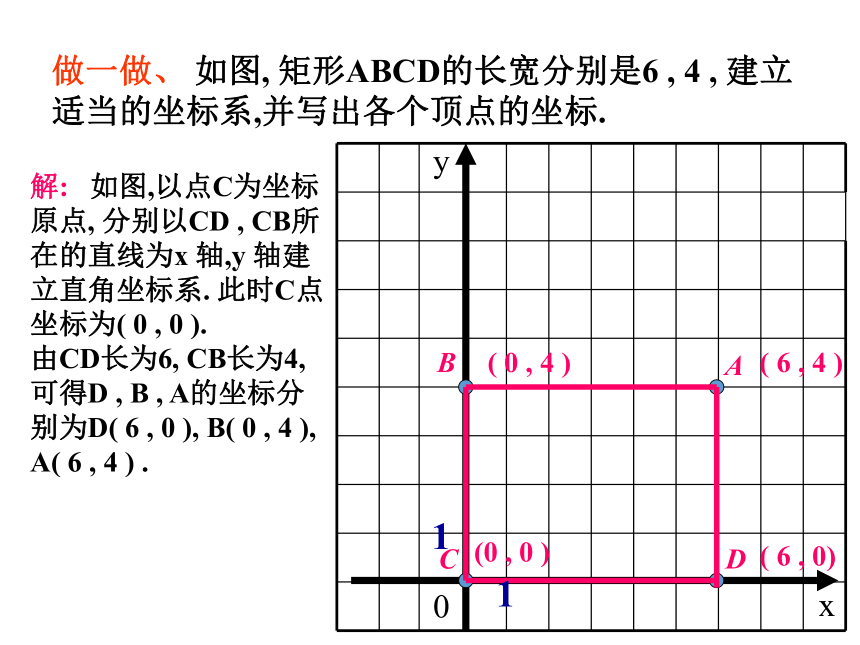
6、坐标平面内的点与谁是一一对应的?其中的两层含义是什么?知识回顾x轴或横轴y轴或纵轴平面直角坐标系第一象限第二象限第三象限第四象限P(-3,2)原点注:坐标轴上的点不属于任何象限温故知新DABC探究一 正方形ABCD的边长为6 ,如果以点A为坐标原点,AB所在直线为x轴,建立平面直角坐标系,那么y轴是哪条线?写出正方形的顶点A、B、C、D的坐标.(6,0)(6,6)(0,6)(0,0)新知探究 请另建立一个平面直角坐标系,这时正方形的顶点A,B,C,D的坐标又分别是多少?与同学交流一下.做一做、 如图, 矩形ABCD的长宽分别是6 , 4 , 建立适当的坐标系,并写出各个顶点的坐标. BCDA解: 如图,以点C为坐标
原点, 分别以CD , CB所
在的直线为x 轴,y 轴建
立直角坐标系. 此时C点
坐标为( 0 , 0 ).
由CD长为6, CB长为4,
可得D , B , A的坐标分
别为D( 6 , 0 ), B( 0 , 4 ),
A( 6 , 4 ) .
xy0(0 , 0 )( 0 , 4 )( 6 , 4 )( 6 , 0)11如图, 矩形ABCD的长宽分别是6 , 4 ,建立适当的坐标系,并写出各个顶点的坐标. BCDA解: 如图,分别以两对边
中点的连线为x 轴,y 轴
建立直角坐标系. 此时
各顶点坐标为A( 3 , 2),
B( -3 , 2 ),C( -3 , -2 ), D( 3 , -2 ) .
xy0(-3, -2 )( -3 , 2)( 3, 2 )( 3 , -2)11点A与点 D关于X轴对称
横坐标相同,
纵坐标互为相反数点A与点 B关于Y轴对称
纵坐标相同,
横坐标互为相反数点A与点 C关于原点对称
横坐标、纵坐标
均互为相反数归纳:
1、在建立平面直角坐标系时要适当,一般建立时能使表示的点的坐标越简单、越容易表示就越适当。
2、在建立平面直角坐标系时要首先规定谁是x轴、谁是y,谁是原点、正方向,并规定了适当的单位长度,然后再用坐标确定点的位置
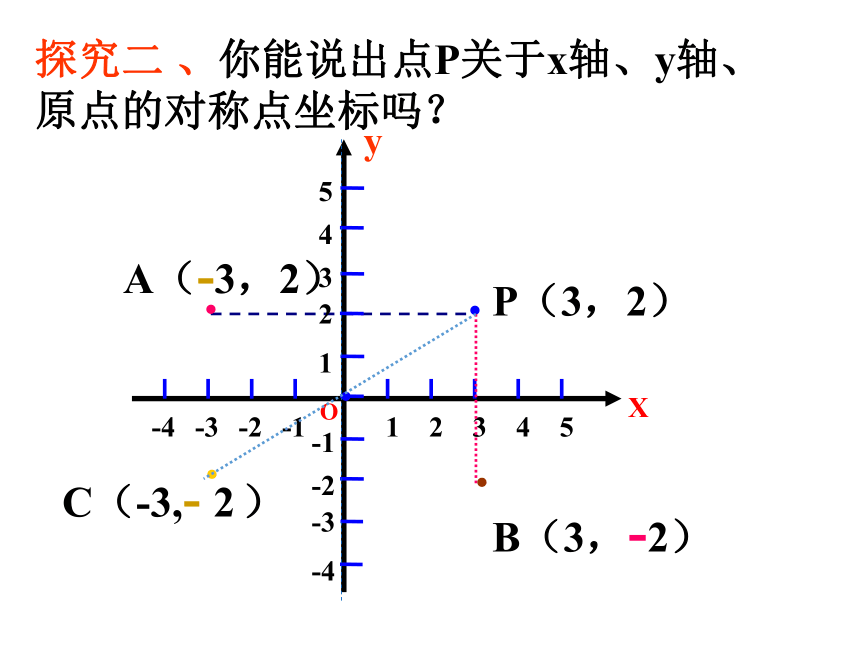
没有一成不变的模式, 但选择适当的坐标系, 可使计算降低难度!方便 , 简单!123·OXP(3,2)·B(3,-2)A(-3,2)C(-3,- 2 ) ··探究二 、你能说出点P关于x轴、y轴、原点的对称点坐标吗?·★若设点M(a,b),
M点关于X轴的对称点M1( )
M点关于Y轴的对称点M2( ),
M点关于原点O的对称点M3( )a,-b- a, b-a,-b探究三、拓展
1.点到坐标轴的距离例:
点A(2,3)到x轴的距离是3,到y轴的距离是2点B(-5,4)到x轴的距离是4,到y轴的距离是5点C(-2,-3)到x轴的距离是3,到y轴的距离是2点D(2,3)到x轴的距离是3,到y轴的距离是2A(1)关于坐标轴、原点对称的点的坐标(3,2)(3,-2)-2-14321-3-4y123-3-1-2(-3,2)(-3,-2)0P(x,y)关于原点的对称点P(-x,-y)A BCDP(x,y)关于y轴的对称点P(-x, y)P(x,y)关于x轴的对称点P(x,-y)3.若点(a,b)关于y轴的对称点在第二象限,则a__0,b__0.><一练习1.点(4,3)与点(4,- 3)的关系是_____
2.点(m,- 1)和点(2,n)关于 x轴对称,则 mn等于( ) (A)- 2 (B)2 (C)1 (D)- 1关于 x轴对称B(1)象限角平分线上的点的坐标xyABx = yx = - y1.已知点A(a, 3)在第一三象限角平分线上,则a=___
2.已知点A(-2,m)在第二四象限角平分线上,则m=___323.已知点A(-3+a,2b+9)在第二象限的角平分线上,且a、 b互为相反数,则a、b的值分别是____________。6,-62. 特殊位置点的坐标(3,4)(-4,4)(4,-4)C(-6,-3)AG·B··E·(-6,0)DK(-3,-4)J··(-6,2)(4,2)· 线段AK、EG与X轴有什么位置关系?点A点K的纵坐标有什么特点?点E点G呢? 线段BD、GJ与X轴有什么位置关系?点B点D的横坐标有什么特点? 点G点J呢?(2)与坐标轴平行的直线上的点的特点平行于横轴的直线上的点的纵坐标相同;
平行于纵轴的直线上的点的横坐标相同;
纵坐标相同的点的连线平行于x轴;
横坐标相同的点的连线平行于y轴。
知识梳理
2.⑴ x轴上的点,纵坐标为0。
y轴上的点,横坐标为0。
⑵ 第一、三象限夹角平分线上的点,纵横坐标相等。
第二、四象限夹角平分线上的点,纵横坐标互为相反数。
⑶与x轴平行(或与y轴垂直)的直线上的点纵坐标都相同。
与y轴平行(或与x轴垂直)的直线上的点横坐标都相同。
(4)平面直角坐标系中有一点P(a , b),
点P到x轴的距离是这个点的 纵坐标的绝对值;
点P到y轴的距离是这个点的横坐标的绝对值;
1.你认为怎样建立适合的直角坐标系?议一议1.在上面的例题中,你还可以怎样
建立直角坐标系? 没有一成不变的模式, 但选择适当的坐标系,
可使计算降低难度!方便 , 简单!
1.点M(-8,12)到x轴的距离是_____,到y轴的距离是_____.1282.如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( ) (A)平行于x轴 (B)平行于y轴
(C)经过原点 (D)以上都不对B3.点A在x轴上,距离原点4个单位长度,则A点的坐标是
_______________。
(4,0)或(-4,0)4.若点P在第三象限且到x轴的距离为 2 ,
到y轴的距离为1.5,则点P的坐标是___________。
(-1.5,-2)随堂练习5.在下图的直角坐标系中描出下列各点,并把各点用线段依次连接起来. 观察它是什么形状的图形?
(2,2),(5,6),(-4,6),(-7,2)平行四边形游戏6.五位同学做游戏,位置如图,建立适当的直角坐标系,写出这五个同学所在位置的坐标.
2、如何由点求坐标?
3、如何由坐标描点?
4、各个象限内点的坐标符号特征是什么?
5、坐标轴上点的坐标特征是什么?
6、坐标平面内的点与谁是一一对应的?其中的两层含义是什么?知识回顾x轴或横轴y轴或纵轴平面直角坐标系第一象限第二象限第三象限第四象限P(-3,2)原点注:坐标轴上的点不属于任何象限温故知新DABC探究一 正方形ABCD的边长为6 ,如果以点A为坐标原点,AB所在直线为x轴,建立平面直角坐标系,那么y轴是哪条线?写出正方形的顶点A、B、C、D的坐标.(6,0)(6,6)(0,6)(0,0)新知探究 请另建立一个平面直角坐标系,这时正方形的顶点A,B,C,D的坐标又分别是多少?与同学交流一下.做一做、 如图, 矩形ABCD的长宽分别是6 , 4 , 建立适当的坐标系,并写出各个顶点的坐标. BCDA解: 如图,以点C为坐标
原点, 分别以CD , CB所
在的直线为x 轴,y 轴建
立直角坐标系. 此时C点
坐标为( 0 , 0 ).
由CD长为6, CB长为4,
可得D , B , A的坐标分
别为D( 6 , 0 ), B( 0 , 4 ),
A( 6 , 4 ) .
xy0(0 , 0 )( 0 , 4 )( 6 , 4 )( 6 , 0)11如图, 矩形ABCD的长宽分别是6 , 4 ,建立适当的坐标系,并写出各个顶点的坐标. BCDA解: 如图,分别以两对边
中点的连线为x 轴,y 轴
建立直角坐标系. 此时
各顶点坐标为A( 3 , 2),
B( -3 , 2 ),C( -3 , -2 ), D( 3 , -2 ) .
xy0(-3, -2 )( -3 , 2)( 3, 2 )( 3 , -2)11点A与点 D关于X轴对称
横坐标相同,
纵坐标互为相反数点A与点 B关于Y轴对称
纵坐标相同,
横坐标互为相反数点A与点 C关于原点对称
横坐标、纵坐标
均互为相反数归纳:
1、在建立平面直角坐标系时要适当,一般建立时能使表示的点的坐标越简单、越容易表示就越适当。
2、在建立平面直角坐标系时要首先规定谁是x轴、谁是y,谁是原点、正方向,并规定了适当的单位长度,然后再用坐标确定点的位置
没有一成不变的模式, 但选择适当的坐标系, 可使计算降低难度!方便 , 简单!123·OXP(3,2)·B(3,-2)A(-3,2)C(-3,- 2 ) ··探究二 、你能说出点P关于x轴、y轴、原点的对称点坐标吗?·★若设点M(a,b),
M点关于X轴的对称点M1( )
M点关于Y轴的对称点M2( ),
M点关于原点O的对称点M3( )a,-b- a, b-a,-b探究三、拓展
1.点到坐标轴的距离例:
点A(2,3)到x轴的距离是3,到y轴的距离是2点B(-5,4)到x轴的距离是4,到y轴的距离是5点C(-2,-3)到x轴的距离是3,到y轴的距离是2点D(2,3)到x轴的距离是3,到y轴的距离是2A(1)关于坐标轴、原点对称的点的坐标(3,2)(3,-2)-2-14321-3-4y123-3-1-2(-3,2)(-3,-2)0P(x,y)关于原点的对称点P(-x,-y)A BCDP(x,y)关于y轴的对称点P(-x, y)P(x,y)关于x轴的对称点P(x,-y)3.若点(a,b)关于y轴的对称点在第二象限,则a__0,b__0.><一练习1.点(4,3)与点(4,- 3)的关系是_____
2.点(m,- 1)和点(2,n)关于 x轴对称,则 mn等于( ) (A)- 2 (B)2 (C)1 (D)- 1关于 x轴对称B(1)象限角平分线上的点的坐标xyABx = yx = - y1.已知点A(a, 3)在第一三象限角平分线上,则a=___
2.已知点A(-2,m)在第二四象限角平分线上,则m=___323.已知点A(-3+a,2b+9)在第二象限的角平分线上,且a、 b互为相反数,则a、b的值分别是____________。6,-62. 特殊位置点的坐标(3,4)(-4,4)(4,-4)C(-6,-3)AG·B··E·(-6,0)DK(-3,-4)J··(-6,2)(4,2)· 线段AK、EG与X轴有什么位置关系?点A点K的纵坐标有什么特点?点E点G呢? 线段BD、GJ与X轴有什么位置关系?点B点D的横坐标有什么特点? 点G点J呢?(2)与坐标轴平行的直线上的点的特点平行于横轴的直线上的点的纵坐标相同;
平行于纵轴的直线上的点的横坐标相同;
纵坐标相同的点的连线平行于x轴;
横坐标相同的点的连线平行于y轴。
知识梳理
2.⑴ x轴上的点,纵坐标为0。
y轴上的点,横坐标为0。
⑵ 第一、三象限夹角平分线上的点,纵横坐标相等。
第二、四象限夹角平分线上的点,纵横坐标互为相反数。
⑶与x轴平行(或与y轴垂直)的直线上的点纵坐标都相同。
与y轴平行(或与x轴垂直)的直线上的点横坐标都相同。
(4)平面直角坐标系中有一点P(a , b),
点P到x轴的距离是这个点的 纵坐标的绝对值;
点P到y轴的距离是这个点的横坐标的绝对值;
1.你认为怎样建立适合的直角坐标系?议一议1.在上面的例题中,你还可以怎样
建立直角坐标系? 没有一成不变的模式, 但选择适当的坐标系,
可使计算降低难度!方便 , 简单!
1.点M(-8,12)到x轴的距离是_____,到y轴的距离是_____.1282.如果同一直角坐标系下两个点的横坐标相同,那么过这两点的直线( ) (A)平行于x轴 (B)平行于y轴
(C)经过原点 (D)以上都不对B3.点A在x轴上,距离原点4个单位长度,则A点的坐标是
_______________。
(4,0)或(-4,0)4.若点P在第三象限且到x轴的距离为 2 ,
到y轴的距离为1.5,则点P的坐标是___________。
(-1.5,-2)随堂练习5.在下图的直角坐标系中描出下列各点,并把各点用线段依次连接起来. 观察它是什么形状的图形?
(2,2),(5,6),(-4,6),(-7,2)平行四边形游戏6.五位同学做游戏,位置如图,建立适当的直角坐标系,写出这五个同学所在位置的坐标.
