6.2 平行四边形的判定(2)同步练习
文档属性
| 名称 | 6.2 平行四边形的判定(2)同步练习 |  | |
| 格式 | doc | ||
| 文件大小 | 516.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-08 09:13:16 | ||
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
6.2 平行四边形的判定(2)同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.对角线互相平分的四边形是平行四边形.
2.如果两条直线互相平行,则其中一条直线上任意两点 到另一条直线的距离相等,这个距离称为平行线之间的距离 .
3.综合运用平行四边形的性质与判定解决有关平行四边形问题.
基础知识和能力拓展精练
一、选择题
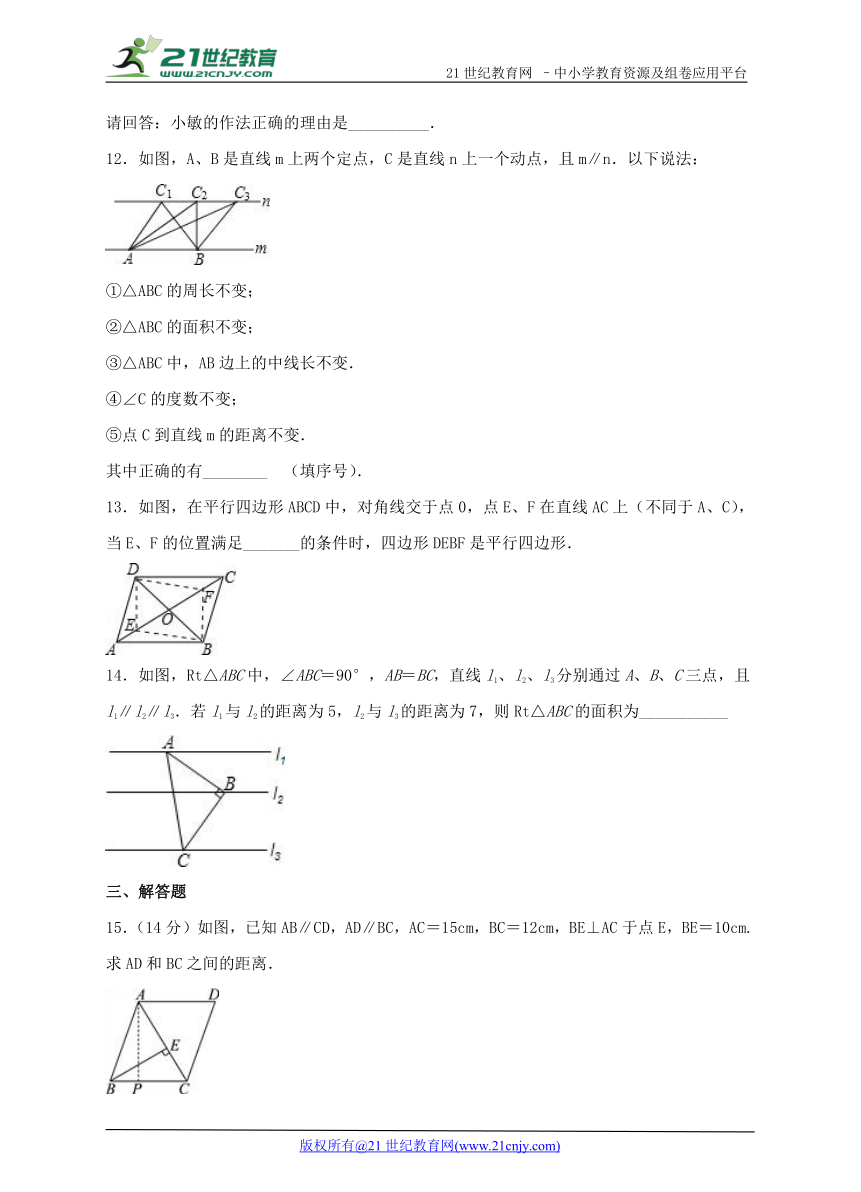
1.如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
A. AB∥CD,AD∥BC B. OA=OC,OB=OD C. AD=BC,AB∥CD D. AB=CD,AD=BC
2.如图,AB∥DC,ED∥BC,AE∥BD,那么图中和△ABD面积相等的三角形(不包含△ABD)有( )
A. 1个 B. 2个 C. 3个 D. 4个
3.如图,a∥b,若要使△ABC的面积与△DEF的面积相等,需增加条件( )
A. AB=DE B. AC=DF C. BC=EF D. BE=AD
4.到直线l的距离等于2 cm的点有( )
A. 0个 B. 1个 C. 无数个 D. 无法确定
5.(吉安永新县期末)如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动.当四边形PQBC为平行四边形时,运动时间为( )
A. 4s B. 3s C. 2s D. 1s
6.下面几组条件中,能判断一个四边形是平行四边形的是( )
A.一组对边相等 B.两条对角线互相平分
C.一组对边平行 D.两条对角线互相垂直
7.如图,在 ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点,当E,F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )
A. AE=CF B. DE=BF C. ∠ADE=∠CBF D. ∠AED=∠CFB
8.如图,P是直线m上一动点,A,B是直线n上的两个定点,且直线m∥n.对于下列各值:①点P到直线n的距离;②△PAB的周长;③△PAB的面积;④∠APB的大小. 其中会随点P的移动而变化的是( )
A. ①② B. ①③ C. ②④ D. ③④
二、填空题
9.如图,四边形ABCD的对角线相交于点O,AO=CO,请添加一个条件_________
(只添一个即可),使四边形ABCD是平行四边形
10.如图,在□ABCD中,两条对角线相交于点O,点E、F、G、H分别是OA、OB、OC、OD的中点,以图中的任意四点(即点A、B、C、D、E、F、G、H、O中的任意四点)为顶点的平行四边形共有________个.
11.阅读下面材料:
在数学课上,老师提出如下问题:
已知:如图,及边的中点.
求作:平行四边形.
①连接并延长,在延长线上截取;
②连接、.
所以四边形就是所求作的平行四边形.
老师说:“小敏的作法正确.
请回答:小敏的作法正确的理由是__________.
12.如图,A、B是直线m上两个定点,C是直线n上一个动点,且m∥n.以下说法:
①△ABC的周长不变;
②△ABC的面积不变;
③△ABC中,AB边上的中线长不变.
④∠C的度数不变;
⑤点C到直线m的距离不变.
其中正确的有________ (填序号).
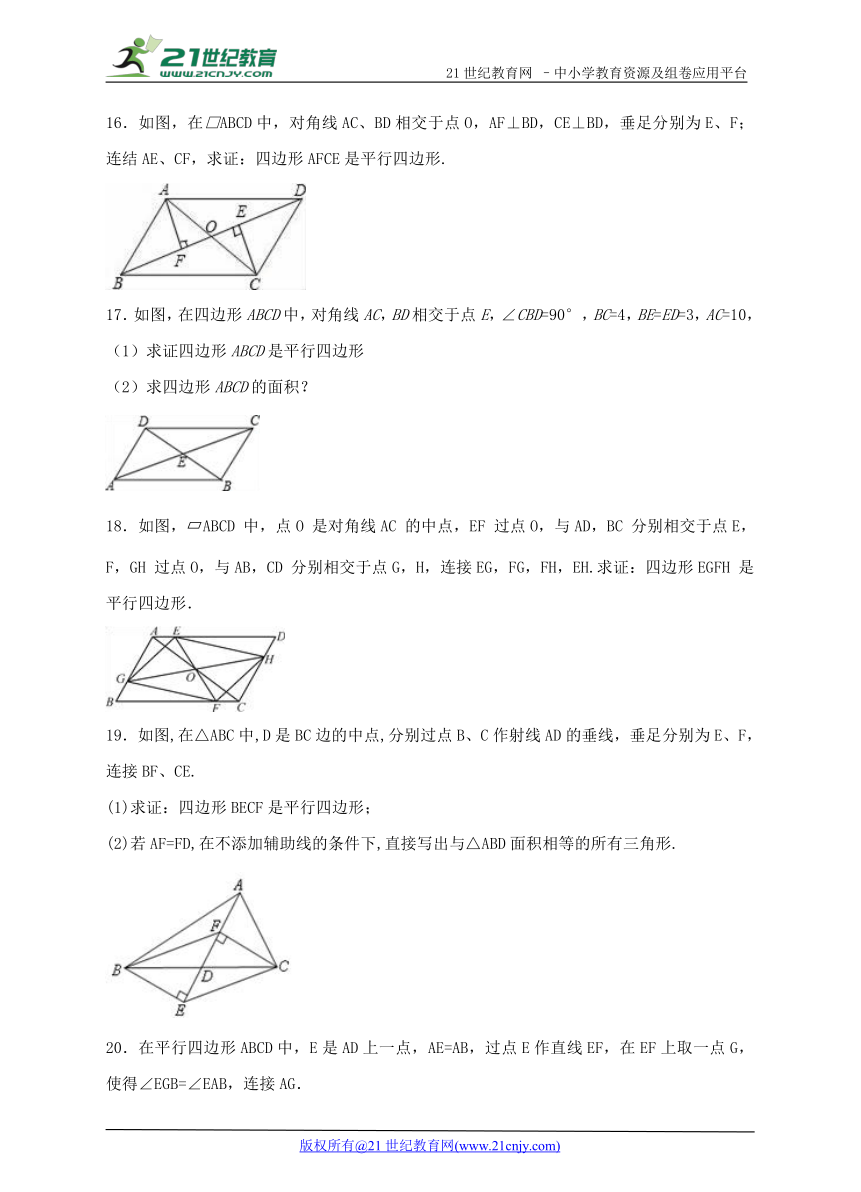
13.如图,在平行四边形ABCD中,对角线交于点0,点E、F在直线AC上(不同于A、C),当E、F的位置满足_______的条件时,四边形DEBF是平行四边形.
14.如图,Rt△ABC中,∠ABC=90°,AB=BC,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3.若l1与l2的距离为5,l2与l3的距离为7,则Rt△ABC的面积为___________
三、解答题
15.(14分)如图,已知AB∥CD,AD∥BC,AC=15cm,BC=12cm,BE⊥AC于点E,BE=10cm.求AD和BC之间的距离.
16.如图,在□ABCD中,对角线AC、BD相交于点O,AF⊥BD,CE⊥BD,垂足分别为E、F;连结AE、CF,求证:四边形AFCE是平行四边形.
17.如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,
(1)求证四边形ABCD是平行四边形
(2)求四边形ABCD的面积?
18.如图, ABCD 中,点O 是对角线AC 的中点,EF 过点O,与AD,BC 分别相交于点E,F,GH 过点O,与AB,CD 分别相交于点G,H,连接EG,FG,FH,EH.求证:四边形EGFH 是平行四边形.
19.如图,在△ABC中,D是BC边的中点,分别过点B、C作射线AD的垂线,垂足分别为E、F,连接BF、CE.
(1)求证:四边形BECF是平行四边形;
(2)若AF=FD,在不添加辅助线的条件下,直接写出与△ABD面积相等的所有三角形.
20.在平行四边形ABCD中,E是AD上一点,AE=AB,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.
(1)如图①,当EF与AB相交时,若∠EAB=60°,求证:EG=AG+BG;
(2)如图②,当EF与CD相交时,且∠EAB=90°,请你写出线段EG、AG、BG之间的数量关系,并证明你的结论.
参考答案
1.D
【解析】由两组对边分别平行的四边形是平行四边形可知A正确;
由对角线互相平分的四边形是平行四边形可知B正确;
由一组对边既平行又相等的四边形是平行四边形可知C不正确;
由两组对边分别相等的四边形是平行四边形可知D正确;
故选C
2.B
【解析】试题分析:根据AB∥CD可得:△ABD和△ABC的面积相等;根据AE∥BD可得:△ABD和△BDE的面积相等;故本题选B.
点睛:本题主要考查的就是平行线之间的距离的性质,属于基础题型.两条平行线之间的距离是处处相等的,我们可以利用这个性质来求三角形面积之间的关系,面积之比就等于底之比.有时候会出现三条平行线,两个三角形的底相同,高不同,然后求面积,这个时候三角形的面积之比就等于高之比.
3.C
【解析】试题分析:两条平行线之间的距离处处相等,则△ABC和△DEF的高相等,则要使面积相等必须满足底相等,故本题选C.
4.C
【解析】试题解析:∵两条平行线间的距离相等,
∴到直线l的距离等于2cm的点有无数个.
故选C.
5.B
【解析】试题解析:设运动时间为t秒,则CP=12-3t,BQ=t,
根据题意得到12-3t=t,
解得:t=3,
故选B.
6.B
【解析】
试题分析:平行四边形的五种判定方法分别是:(1)两组对边分别平行的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形;(4)两组对角分别相等的四边形是平行四边形;(5)对角线互相平分的四边形是平行四边形.根据平行四边形的判定方法,采用排除法,逐项分析判断.
解:A、一组对边相等,不能判断,故错误;
B、两条对角线互相平分,能判断,故正确;
C、一组对边平行,不能判断,故错误;
D、两条对角线互相垂直,不能判断,故错误.
故选:B.
7.B
【解析】A选项:∵在平行四边形ABCD中,OA=OC,OB=OD,
若AE=CF,则OE=OF,
∴四边形DEBF是平行四边形;
B选项:若DE与AC不垂直,则满足AC上一定有一点DM=DE,同理有一点N使BF=BN,则四边形DEBF不一定是平行四边形,则选项错误;
C选项:∵在平行四边形ABCD中,OB=OD,AD∥BC,
∴∠ADB=∠CBD,
若∠ADE=∠CBF,则∠DEB=∠FBO,
则△DOE和△BOF中,
∴△DOE≌△BOF,
∴DE=BF,
又∵DE∥BF,
∴四边形DEBF是平行四边形.故选项正确;
D选项:∵∠AED=∠CFB,
∴∠DEO=∠BFO,
∴DE∥BF,
在△DOE和△BOF中,
∴△DOE≌△BOF,
∴DE=BF,
∴四边形DEBF是平行四边形.故选项正确.
故选B.
8.C
【解析】∵直线m∥n,∴点P到直线n的距离不变.
∵PA,PB的长度随点P的移动而变化,
∴△PAB的周长会随点P的移动而变化.
∵点P到直线n的距离不变,AB的大小不变,∴△PAB的面积不变.
∵点P在直线m上移动,∴∠APB的大小随点P的移动而变化.
综上所述,会随点P的移动而变化的是②④.
点睛:根据平行线间的距离不变从而判断出①不变;再根据三角形的周长的定义判断出②是变化的;然后根据等底等高的三角形的面积相等确定出③不变;根据角的定义判断出④变化.
9.BO=DO
【解析】解:∵AO=CO,BO=DO,∴四边形ABCD是平行四边形.故答案为:BO=DO.
10.4
【解析】如图:
即□EFGH,□ABCD,□BEDG,□AFCH,
故答案为:4.
11.对角线互相平分的四边形是平行四边形
【解析】试题解析:∵是边的中点,
∴,
∵,
∴四边形是平行四边形,
则依据:对角线互相平分的四边形是平行四边形.
故答案为:对角线互相平分的四边形是平行四边形.
12.②⑤
【解析】①∵当点C运动时,AC+BC的值不固定,
∴△ABC的周长不确定,
∴①错误;
②∵m∥n,
∴C到AB的距离相等,
设距离为d,
则△ABC的面积=×AB×d,
∴△ABC的面积不变,
∴②正确;
③∵当点C运动时,
∴连接点C和AB的中点的线段的长不确定,
∴③错误;
④∵当点C运动时,
∴∠ACB的大小不确定,
∴④错误;
⑤∵m∥n,
∴点C到直线m的距离不变,
∴⑤正确;
故答案为:②⑤.
点睛:本题考查的是平行线之间的距离和三角形的面积的计算,掌握平行线间的距离处处相等是解题的关键.
13.AE=CF(答案不唯一)
【解析】试题解析: 当AE=CF时四边形DEBF是平行四边形;
∵四边形ABCD是平行四边形,
∴DO=BO,AO=CO,
∵AE=CF,
∴EO=FO,
∴四边形DEBF是平行四边形,
故答案为:AE=CF.
14.37
【解析】
过点B作EF⊥l2,交l1于E,交l3于F,如 图,
∵EF⊥l2,l1∥l2∥l3,
∴EF⊥l1⊥l3,
∴∠ABE+∠EAB=90°,∠AEB=∠BFC=90°,
又∵∠ABC=90°,
∴∠ABE+∠FBC=90°,
∴∠EAB=∠FBC,
在△ABE和△BCF中,
,
∴△ABE≌△BCF,
∴BE=CF=5,AE=BF=7,
在Rt△ABE中,AB2=BE2+AE2,
∴AB2=74,
∴S△ABC=AB BC=AB2=37.
故答案是37.
点睛:本题考查了全等三角形的判定和性质、勾股定理、平行线间的距离,三角形的面积公式,解题的关键是做辅助线,构造全等三角形,通过证明三角形全等对应边相等,再利用三角形的面积公式即可得解.
15.12.5cm
【解析】试题分析:首先过点A作出AD和BC之间的距离,然后根据AC和BE的长度求出△ABC的面积,然后根据 EMBED Equation.DSMT4 ×BC×AP=△ABC的面积求出AP的长度,即AD和BC 之间的距离.
试题解析:解:过点A作BC的垂线,交BC于P点,三角形ABC的面积为×AC×BE=×15×10=75(cm2),又因为三角形ABC的面积为×BC×AP=×12×AP=75,所以AP=12.5cm.因此AD和BC之间的距离为12.5cm.
点睛:本题主要考查的就是利用等积法求线段之间的距离,属于简单题型.在求直角三角形斜边上的高线时,我们也是利用等积法来进行计算的,很多同学会和斜边上的中线混淆在一起.等积法在几何求某线段长度的时候会经常用到,同学们一定要非常熟练地掌握这个方法.
16.见解析
【解析】整体分析:
用SAS证明△AOF≌△COE,得到OF=OE,由对角线互相平分的四边形是平行四边形求证.
证明:连接AE,CF.
∵四边形ABCD是平行四边形,
∴AO=OC.
∵AF⊥BD,CE⊥BD,
∴∠AFO=∠CEO=90°.
在△AOF与△COE中
∠AFO=∠CFO=90°,AO=OC,∠AOF=∠COE,
∴△AOF≌△COE(AAS),
∴OF=OE,
∴四边形AECF是平行四边形.
17.(1)见解析;(2)面积=24
【解析】整体分析:
根据勾股定理,可得EC的长,根据对角线互相平分的四边形是平行四边形,可得四边形ABCD的形状,根据平行四边形的面积公式,即可求解.
(1)证明:在Rt△BCE中,由勾股定理得:
CE===5.
∵BE=DE=3,AE=CE=5,
∴四边形ABCD是平行四边形;
(2)解:平行四边形ABCD的面积为BC BD=4×(3+3)=24.
所以平行四边形ABCD的面积为24.
18.证明见解析.
【解析】试题分析: 由四边形ABCD是平行四边形,得到AD∥BC,根据平行四边形的性质得到∠EAO=∠FCO,证出△OAE≌△OCF,得到OE=OF,同理OG=OH,根据对角线互相平分的四边形是平行四边形得到结论.
试题解析:
∵四边形ABCD 为平行四边形,
∴AD∥BC.
∴∠EAO=∠FCO.
∵O为AC的中点,
∴OA=OC.
在△OAE和△OCF中,
∴△OAE≌△OCF(ASA).
∴OE=OF.
同理可证得OG=OH.
∴四边形EGFH是平行四边形.
点睛: 此题主要考查了平行四边形的性质与判定,关键是掌握平行四边形对角线互相平分,对角线互相平分的四边形是平行四边形.
19.(1)详见解析;(2)详见解析.
【解析】试题分析:(1)由D是BC中点,得到BD=CD,通过AAS证明△BED≌△CFD,得到ED=FD,再由对角线互相平分的四边形是平行四边形即可得到结论;
(2)与△ABD面积相等的三角形有△ACD、△CEF、△BEF、△BEC、△BFC.
试题解析:(1)证明:∵D是BC中点,∴BD=CD.
∵BE⊥AE,CF⊥AE,∴∠BED=∠CFD=900.在△BED与△CFD中,∵∠BED=∠CFD,∠BDE=∠CDF,BD=CD,∴△BED≌△CFD(AAS),∴ED=FD .∵BD=CD,∴四边形BFEC是平行四边形.
(2)与△ABD面积相等的三角形有△ACD、△CEF、△BEF、△BEC、△BFC.
20.(1)证明见解析;(2)EG= EMBED Equation.DSMT4 AG﹣BG,理由见解析.
【解析】试题分析:(1)如图,作∠GAH=∠EAB交GE于点H,易证△ABG≌△AEH ,再判定△AGH是等边三角形,即可得结论;(2)EG=AG-BG,如图②,作∠GAH=∠EAB交GE于点H,类比(1)的方法证明△ABG≌△AEH,再判定△AGH是等腰直角三角形,即可得结论.
试题解析:
如图,作∠GAH=∠EAB交GE于点H
∴∠GAB=∠HAE
∵∠EAB =∠EGB,∠APE=∠BPG
∴∠ABG=∠AEH
又∵AB=AE
∴△ABG≌△AEH
∴BG=EH,AG=AH
∵∠GAH=∠EAB=60°
∴△AGH是等边三角形
∴AG=GH
∴EG=AG+BG
(2) EG=AG-BG,
如图②,作∠GAH=∠EAB交GE于点H
∴∠GAB=∠HAE
又∵∠EGB=∠EAB=90°
∴∠ABG+∠AEG=∠AEG+∠AEH=180°
∴∠ABG=∠AEH
又∵AB=AE
∴△ABG≌△AEH
∴BG=EH,AG=AH
又∵∠GAH =∠EAB=90°
∴△AGH是等腰直角三角形
∴AG=HG
∴EG=AG-BG
点睛:本题是一道四边形与三角形的综合题,主要考查了平行四边形的性质、全等三角形的判定及性质、等边三角形的判定及性质、等腰三角形的判定等知识,难度适中,正确作出辅助线是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
6.2 平行四边形的判定(2)同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.对角线互相平分的四边形是平行四边形.
2.如果两条直线互相平行,则其中一条直线上任意两点 到另一条直线的距离相等,这个距离称为平行线之间的距离 .
3.综合运用平行四边形的性质与判定解决有关平行四边形问题.
基础知识和能力拓展精练
一、选择题
1.如图,在四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
A. AB∥CD,AD∥BC B. OA=OC,OB=OD C. AD=BC,AB∥CD D. AB=CD,AD=BC
2.如图,AB∥DC,ED∥BC,AE∥BD,那么图中和△ABD面积相等的三角形(不包含△ABD)有( )
A. 1个 B. 2个 C. 3个 D. 4个
3.如图,a∥b,若要使△ABC的面积与△DEF的面积相等,需增加条件( )
A. AB=DE B. AC=DF C. BC=EF D. BE=AD
4.到直线l的距离等于2 cm的点有( )
A. 0个 B. 1个 C. 无数个 D. 无法确定
5.(吉安永新县期末)如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动.当四边形PQBC为平行四边形时,运动时间为( )
A. 4s B. 3s C. 2s D. 1s
6.下面几组条件中,能判断一个四边形是平行四边形的是( )
A.一组对边相等 B.两条对角线互相平分
C.一组对边平行 D.两条对角线互相垂直
7.如图,在 ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点,当E,F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )
A. AE=CF B. DE=BF C. ∠ADE=∠CBF D. ∠AED=∠CFB
8.如图,P是直线m上一动点,A,B是直线n上的两个定点,且直线m∥n.对于下列各值:①点P到直线n的距离;②△PAB的周长;③△PAB的面积;④∠APB的大小. 其中会随点P的移动而变化的是( )
A. ①② B. ①③ C. ②④ D. ③④
二、填空题
9.如图,四边形ABCD的对角线相交于点O,AO=CO,请添加一个条件_________
(只添一个即可),使四边形ABCD是平行四边形
10.如图,在□ABCD中,两条对角线相交于点O,点E、F、G、H分别是OA、OB、OC、OD的中点,以图中的任意四点(即点A、B、C、D、E、F、G、H、O中的任意四点)为顶点的平行四边形共有________个.
11.阅读下面材料:
在数学课上,老师提出如下问题:
已知:如图,及边的中点.
求作:平行四边形.
①连接并延长,在延长线上截取;
②连接、.
所以四边形就是所求作的平行四边形.
老师说:“小敏的作法正确.
请回答:小敏的作法正确的理由是__________.
12.如图,A、B是直线m上两个定点,C是直线n上一个动点,且m∥n.以下说法:
①△ABC的周长不变;
②△ABC的面积不变;
③△ABC中,AB边上的中线长不变.
④∠C的度数不变;
⑤点C到直线m的距离不变.
其中正确的有________ (填序号).
13.如图,在平行四边形ABCD中,对角线交于点0,点E、F在直线AC上(不同于A、C),当E、F的位置满足_______的条件时,四边形DEBF是平行四边形.
14.如图,Rt△ABC中,∠ABC=90°,AB=BC,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3.若l1与l2的距离为5,l2与l3的距离为7,则Rt△ABC的面积为___________
三、解答题
15.(14分)如图,已知AB∥CD,AD∥BC,AC=15cm,BC=12cm,BE⊥AC于点E,BE=10cm.求AD和BC之间的距离.
16.如图,在□ABCD中,对角线AC、BD相交于点O,AF⊥BD,CE⊥BD,垂足分别为E、F;连结AE、CF,求证:四边形AFCE是平行四边形.
17.如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,
(1)求证四边形ABCD是平行四边形
(2)求四边形ABCD的面积?
18.如图, ABCD 中,点O 是对角线AC 的中点,EF 过点O,与AD,BC 分别相交于点E,F,GH 过点O,与AB,CD 分别相交于点G,H,连接EG,FG,FH,EH.求证:四边形EGFH 是平行四边形.
19.如图,在△ABC中,D是BC边的中点,分别过点B、C作射线AD的垂线,垂足分别为E、F,连接BF、CE.
(1)求证:四边形BECF是平行四边形;
(2)若AF=FD,在不添加辅助线的条件下,直接写出与△ABD面积相等的所有三角形.
20.在平行四边形ABCD中,E是AD上一点,AE=AB,过点E作直线EF,在EF上取一点G,使得∠EGB=∠EAB,连接AG.
(1)如图①,当EF与AB相交时,若∠EAB=60°,求证:EG=AG+BG;
(2)如图②,当EF与CD相交时,且∠EAB=90°,请你写出线段EG、AG、BG之间的数量关系,并证明你的结论.
参考答案
1.D
【解析】由两组对边分别平行的四边形是平行四边形可知A正确;
由对角线互相平分的四边形是平行四边形可知B正确;
由一组对边既平行又相等的四边形是平行四边形可知C不正确;
由两组对边分别相等的四边形是平行四边形可知D正确;
故选C
2.B
【解析】试题分析:根据AB∥CD可得:△ABD和△ABC的面积相等;根据AE∥BD可得:△ABD和△BDE的面积相等;故本题选B.
点睛:本题主要考查的就是平行线之间的距离的性质,属于基础题型.两条平行线之间的距离是处处相等的,我们可以利用这个性质来求三角形面积之间的关系,面积之比就等于底之比.有时候会出现三条平行线,两个三角形的底相同,高不同,然后求面积,这个时候三角形的面积之比就等于高之比.
3.C
【解析】试题分析:两条平行线之间的距离处处相等,则△ABC和△DEF的高相等,则要使面积相等必须满足底相等,故本题选C.
4.C
【解析】试题解析:∵两条平行线间的距离相等,
∴到直线l的距离等于2cm的点有无数个.
故选C.
5.B
【解析】试题解析:设运动时间为t秒,则CP=12-3t,BQ=t,
根据题意得到12-3t=t,
解得:t=3,
故选B.
6.B
【解析】
试题分析:平行四边形的五种判定方法分别是:(1)两组对边分别平行的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形;(4)两组对角分别相等的四边形是平行四边形;(5)对角线互相平分的四边形是平行四边形.根据平行四边形的判定方法,采用排除法,逐项分析判断.
解:A、一组对边相等,不能判断,故错误;
B、两条对角线互相平分,能判断,故正确;
C、一组对边平行,不能判断,故错误;
D、两条对角线互相垂直,不能判断,故错误.
故选:B.
7.B
【解析】A选项:∵在平行四边形ABCD中,OA=OC,OB=OD,
若AE=CF,则OE=OF,
∴四边形DEBF是平行四边形;
B选项:若DE与AC不垂直,则满足AC上一定有一点DM=DE,同理有一点N使BF=BN,则四边形DEBF不一定是平行四边形,则选项错误;
C选项:∵在平行四边形ABCD中,OB=OD,AD∥BC,
∴∠ADB=∠CBD,
若∠ADE=∠CBF,则∠DEB=∠FBO,
则△DOE和△BOF中,
∴△DOE≌△BOF,
∴DE=BF,
又∵DE∥BF,
∴四边形DEBF是平行四边形.故选项正确;
D选项:∵∠AED=∠CFB,
∴∠DEO=∠BFO,
∴DE∥BF,
在△DOE和△BOF中,
∴△DOE≌△BOF,
∴DE=BF,
∴四边形DEBF是平行四边形.故选项正确.
故选B.
8.C
【解析】∵直线m∥n,∴点P到直线n的距离不变.
∵PA,PB的长度随点P的移动而变化,
∴△PAB的周长会随点P的移动而变化.
∵点P到直线n的距离不变,AB的大小不变,∴△PAB的面积不变.
∵点P在直线m上移动,∴∠APB的大小随点P的移动而变化.
综上所述,会随点P的移动而变化的是②④.
点睛:根据平行线间的距离不变从而判断出①不变;再根据三角形的周长的定义判断出②是变化的;然后根据等底等高的三角形的面积相等确定出③不变;根据角的定义判断出④变化.
9.BO=DO
【解析】解:∵AO=CO,BO=DO,∴四边形ABCD是平行四边形.故答案为:BO=DO.
10.4
【解析】如图:
即□EFGH,□ABCD,□BEDG,□AFCH,
故答案为:4.
11.对角线互相平分的四边形是平行四边形
【解析】试题解析:∵是边的中点,
∴,
∵,
∴四边形是平行四边形,
则依据:对角线互相平分的四边形是平行四边形.
故答案为:对角线互相平分的四边形是平行四边形.
12.②⑤
【解析】①∵当点C运动时,AC+BC的值不固定,
∴△ABC的周长不确定,
∴①错误;
②∵m∥n,
∴C到AB的距离相等,
设距离为d,
则△ABC的面积=×AB×d,
∴△ABC的面积不变,
∴②正确;
③∵当点C运动时,
∴连接点C和AB的中点的线段的长不确定,
∴③错误;
④∵当点C运动时,
∴∠ACB的大小不确定,
∴④错误;
⑤∵m∥n,
∴点C到直线m的距离不变,
∴⑤正确;
故答案为:②⑤.
点睛:本题考查的是平行线之间的距离和三角形的面积的计算,掌握平行线间的距离处处相等是解题的关键.
13.AE=CF(答案不唯一)
【解析】试题解析: 当AE=CF时四边形DEBF是平行四边形;
∵四边形ABCD是平行四边形,
∴DO=BO,AO=CO,
∵AE=CF,
∴EO=FO,
∴四边形DEBF是平行四边形,
故答案为:AE=CF.
14.37
【解析】
过点B作EF⊥l2,交l1于E,交l3于F,如 图,
∵EF⊥l2,l1∥l2∥l3,
∴EF⊥l1⊥l3,
∴∠ABE+∠EAB=90°,∠AEB=∠BFC=90°,
又∵∠ABC=90°,
∴∠ABE+∠FBC=90°,
∴∠EAB=∠FBC,
在△ABE和△BCF中,
,
∴△ABE≌△BCF,
∴BE=CF=5,AE=BF=7,
在Rt△ABE中,AB2=BE2+AE2,
∴AB2=74,
∴S△ABC=AB BC=AB2=37.
故答案是37.
点睛:本题考查了全等三角形的判定和性质、勾股定理、平行线间的距离,三角形的面积公式,解题的关键是做辅助线,构造全等三角形,通过证明三角形全等对应边相等,再利用三角形的面积公式即可得解.
15.12.5cm
【解析】试题分析:首先过点A作出AD和BC之间的距离,然后根据AC和BE的长度求出△ABC的面积,然后根据 EMBED Equation.DSMT4 ×BC×AP=△ABC的面积求出AP的长度,即AD和BC 之间的距离.
试题解析:解:过点A作BC的垂线,交BC于P点,三角形ABC的面积为×AC×BE=×15×10=75(cm2),又因为三角形ABC的面积为×BC×AP=×12×AP=75,所以AP=12.5cm.因此AD和BC之间的距离为12.5cm.
点睛:本题主要考查的就是利用等积法求线段之间的距离,属于简单题型.在求直角三角形斜边上的高线时,我们也是利用等积法来进行计算的,很多同学会和斜边上的中线混淆在一起.等积法在几何求某线段长度的时候会经常用到,同学们一定要非常熟练地掌握这个方法.
16.见解析
【解析】整体分析:
用SAS证明△AOF≌△COE,得到OF=OE,由对角线互相平分的四边形是平行四边形求证.
证明:连接AE,CF.
∵四边形ABCD是平行四边形,
∴AO=OC.
∵AF⊥BD,CE⊥BD,
∴∠AFO=∠CEO=90°.
在△AOF与△COE中
∠AFO=∠CFO=90°,AO=OC,∠AOF=∠COE,
∴△AOF≌△COE(AAS),
∴OF=OE,
∴四边形AECF是平行四边形.
17.(1)见解析;(2)面积=24
【解析】整体分析:
根据勾股定理,可得EC的长,根据对角线互相平分的四边形是平行四边形,可得四边形ABCD的形状,根据平行四边形的面积公式,即可求解.
(1)证明:在Rt△BCE中,由勾股定理得:
CE===5.
∵BE=DE=3,AE=CE=5,
∴四边形ABCD是平行四边形;
(2)解:平行四边形ABCD的面积为BC BD=4×(3+3)=24.
所以平行四边形ABCD的面积为24.
18.证明见解析.
【解析】试题分析: 由四边形ABCD是平行四边形,得到AD∥BC,根据平行四边形的性质得到∠EAO=∠FCO,证出△OAE≌△OCF,得到OE=OF,同理OG=OH,根据对角线互相平分的四边形是平行四边形得到结论.
试题解析:
∵四边形ABCD 为平行四边形,
∴AD∥BC.
∴∠EAO=∠FCO.
∵O为AC的中点,
∴OA=OC.
在△OAE和△OCF中,
∴△OAE≌△OCF(ASA).
∴OE=OF.
同理可证得OG=OH.
∴四边形EGFH是平行四边形.
点睛: 此题主要考查了平行四边形的性质与判定,关键是掌握平行四边形对角线互相平分,对角线互相平分的四边形是平行四边形.
19.(1)详见解析;(2)详见解析.
【解析】试题分析:(1)由D是BC中点,得到BD=CD,通过AAS证明△BED≌△CFD,得到ED=FD,再由对角线互相平分的四边形是平行四边形即可得到结论;
(2)与△ABD面积相等的三角形有△ACD、△CEF、△BEF、△BEC、△BFC.
试题解析:(1)证明:∵D是BC中点,∴BD=CD.
∵BE⊥AE,CF⊥AE,∴∠BED=∠CFD=900.在△BED与△CFD中,∵∠BED=∠CFD,∠BDE=∠CDF,BD=CD,∴△BED≌△CFD(AAS),∴ED=FD .∵BD=CD,∴四边形BFEC是平行四边形.
(2)与△ABD面积相等的三角形有△ACD、△CEF、△BEF、△BEC、△BFC.
20.(1)证明见解析;(2)EG= EMBED Equation.DSMT4 AG﹣BG,理由见解析.
【解析】试题分析:(1)如图,作∠GAH=∠EAB交GE于点H,易证△ABG≌△AEH ,再判定△AGH是等边三角形,即可得结论;(2)EG=AG-BG,如图②,作∠GAH=∠EAB交GE于点H,类比(1)的方法证明△ABG≌△AEH,再判定△AGH是等腰直角三角形,即可得结论.
试题解析:
如图,作∠GAH=∠EAB交GE于点H
∴∠GAB=∠HAE
∵∠EAB =∠EGB,∠APE=∠BPG
∴∠ABG=∠AEH
又∵AB=AE
∴△ABG≌△AEH
∴BG=EH,AG=AH
∵∠GAH=∠EAB=60°
∴△AGH是等边三角形
∴AG=GH
∴EG=AG+BG
(2) EG=AG-BG,
如图②,作∠GAH=∠EAB交GE于点H
∴∠GAB=∠HAE
又∵∠EGB=∠EAB=90°
∴∠ABG+∠AEG=∠AEG+∠AEH=180°
∴∠ABG=∠AEH
又∵AB=AE
∴△ABG≌△AEH
∴BG=EH,AG=AH
又∵∠GAH =∠EAB=90°
∴△AGH是等腰直角三角形
∴AG=HG
∴EG=AG-BG
点睛:本题是一道四边形与三角形的综合题,主要考查了平行四边形的性质、全等三角形的判定及性质、等边三角形的判定及性质、等腰三角形的判定等知识,难度适中,正确作出辅助线是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
