13.3等腰三角形的性质 课件(共23张PPT)
文档属性
| 名称 | 13.3等腰三角形的性质 课件(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 683.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-08 07:02:02 | ||
图片预览








文档简介
(共23张PPT)
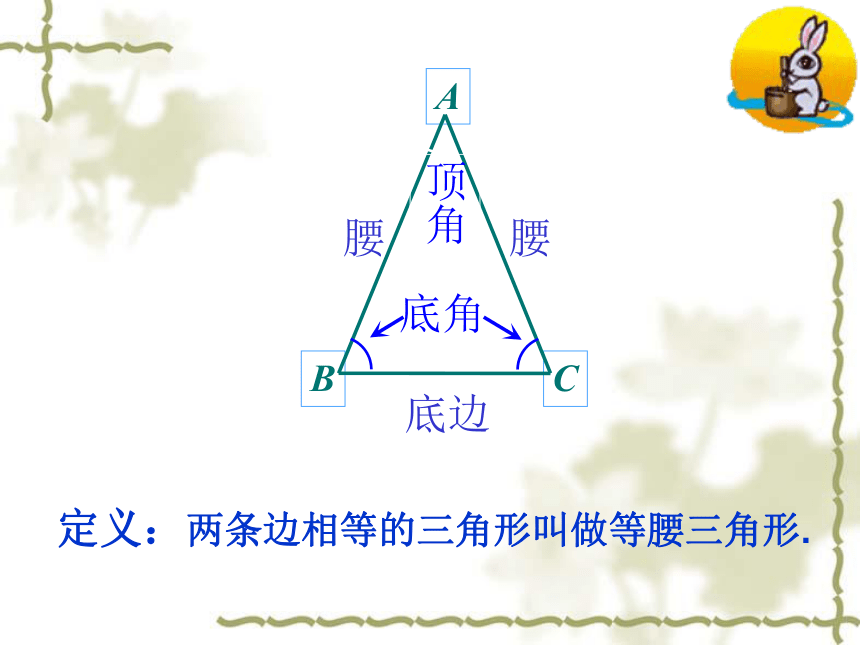
A
B
C
底边
腰
腰
顶角
底角
定义:两条边相等的三角形叫做等腰三角形.
请拿出你经过折叠、剪贴得到的等腰三角形纸片
观察你所得到等腰三角形,你能发现等腰三角形具有哪些性质?
A
B
D
C
等腰三角形两个底角相等.
∠B=∠C
观察你所得到等腰三角形,你能发现等腰三角形具有哪些性质?
已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
1
2
证明:
作顶角的平分线AD. 在△BAD和△CAD中,
AB=AC ( 已知 ),
∠ 1= ∠ 2 ( 辅助线作法 ),
AD=AD (公共边) ,
∴ △BAD ≌ △CAD (SAS).
∴ ∠ B= ∠C (全等三角形的对应角相等).
证明:等腰三角形的两个底角相等
作顶角的平分线
D
证明:
作底边中线AD.
在△BAD和△CAD中,
AB=AC ( 已知 ),
BD=CD ( 辅助线作法 ),
AD=AD (公共边) ,
∴ △BAD ≌ △CAD (SSS).
∴ ∠ B= ∠C (全等三角形的对应角相等).
已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
D
证明:等腰三角形的两个底角相等
作底边中线
证明:
作底边高线AD.
在Rt△BAD和△RtCAD中,
AB=AC ( 已知 ),
AD=AD (公共边) ,
∴ Rt △BAD ≌ Rt △CAD (HL).
∴ ∠ B= ∠C (全等三角形的对应角相等).
已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
D
证明:等腰三角形的两个底角相等
作底边的高线
等腰三角形的性质1:
等腰三角形的两个底角相等
(简写成“等边对等角”)
注意:等边对等角是指
在 三角形中 。
一个
一个
用符号语言表示为:
在△ABC中,
∵ AB=AC
∴ ∠B=∠C ( )
等边对等角
C
A
B
2、等腰三角形一个底角为70°,它的顶角为______.
3、等腰三角形一个内角为70°,它的另外两个角为
__________________.
4、等腰三角形一个内角为100°,它的另外两个角为___________.
40 °
40 °,40 °
70°,40°或55°,55°
1、等腰三角形一个顶角为70°,其它两个角为_________.
55°,55°
是底边上的高,
AD垂直于BC
底边上的中线、
性质2:
等腰三角形的顶角平分线、底边上
的中线、底边上的高相互重合。
简称“等腰三角形三线合一”.
AD平分∠BAC
AD是BC的中线
顶角平分线、
A
B
D
C
观察我们刚才的探索与证明过程,你发现等腰三角形两底角相等外,你还发现了哪些等量关系?
∠1= ∠ 2
∠ADB= ∠ ADC=900
BD=CD
2
1
1、 根据等腰三角形性质定理2,在△ABC中, AB=AC时,
∵AD⊥BC,
∴∠_____ = ∠_____,____= ____.
(2) ∵AD是中线,
∴____⊥____ ,∠_____ =∠_____.
(3) ∵AD是角平分线,
∴____ ⊥____ ,_____ =_____.
A
B
C
D
BAD
CAD
CAD
BD
CD
AD
BC
BD
BAD
BC
AD
CD
2:△ ABC是等腰直角三角形 (AB=AC, ∠ BAC=90°),AD是底 边BC上的高,标出∠ B, ∠ C, ∠ BAD, ∠ DAC的度数?
B
A
C
D
答: ∠ B= ∠ C= ∠ BAD= ∠ DAC=45°
A
C
B
D
如图,是西安半坡博物馆屋顶的截面图,已经知道它的两边AB和AC是相等的.建筑工人师傅对这个建筑物做出了两个判断:
①工人师傅在测量了∠B为37°以后,并没有测量∠C ,就说∠C 的度数也是37°.
②工人师傅要加固屋顶,他们通过测量找到了横梁BC的中点D,然后在AD两点之间钉上一根木桩,他们认为木桩是垂直横梁的.
请同学们想想,工人师傅的说法对吗?请说明理由.
(学以致用)
如图,在△ ABC中,AB=AC,点D在AC上,
且BD=BC=AD。求△ ABC各角的度数。
A
B
C
D
解:∵ AB=AC BD=BC=AD
∴ ∠ABC= ∠ C= ∠ 3
∠ A= ∠1(等边对等角)
设 ∠ A=x,则
∠ 3= ∠ A+ ∠ 1=2x
从而 ∠ ABC= ∠ C= ∠ 3=2x
于是在△ ABC中,有
∠ A+ ∠ ABC+ ∠ C=x+2x+2x=1800
解得 x=360
在 △ABC中, ∠ A=360, ∠ ABC= ∠ C=720
1
2
3
一题多解
如图,点D、E在△ABC的边BC上,
且AB=AC,AD=AE,此时BD与CE有
何关系?请说明理由。
等腰三角形的性质
等边对等角
等腰三角形
三线合一
课本:P56页
第4、7题
作
业
:
A
B
C
底边
腰
腰
顶角
底角
定义:两条边相等的三角形叫做等腰三角形.
请拿出你经过折叠、剪贴得到的等腰三角形纸片
观察你所得到等腰三角形,你能发现等腰三角形具有哪些性质?
A
B
D
C
等腰三角形两个底角相等.
∠B=∠C
观察你所得到等腰三角形,你能发现等腰三角形具有哪些性质?
已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
1
2
证明:
作顶角的平分线AD. 在△BAD和△CAD中,
AB=AC ( 已知 ),
∠ 1= ∠ 2 ( 辅助线作法 ),
AD=AD (公共边) ,
∴ △BAD ≌ △CAD (SAS).
∴ ∠ B= ∠C (全等三角形的对应角相等).
证明:等腰三角形的两个底角相等
作顶角的平分线
D
证明:
作底边中线AD.
在△BAD和△CAD中,
AB=AC ( 已知 ),
BD=CD ( 辅助线作法 ),
AD=AD (公共边) ,
∴ △BAD ≌ △CAD (SSS).
∴ ∠ B= ∠C (全等三角形的对应角相等).
已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
D
证明:等腰三角形的两个底角相等
作底边中线
证明:
作底边高线AD.
在Rt△BAD和△RtCAD中,
AB=AC ( 已知 ),
AD=AD (公共边) ,
∴ Rt △BAD ≌ Rt △CAD (HL).
∴ ∠ B= ∠C (全等三角形的对应角相等).
已知: △ ABC中,AB=AC.
求证: ∠B= ∠C.
A
B
C
D
证明:等腰三角形的两个底角相等
作底边的高线
等腰三角形的性质1:
等腰三角形的两个底角相等
(简写成“等边对等角”)
注意:等边对等角是指
在 三角形中 。
一个
一个
用符号语言表示为:
在△ABC中,
∵ AB=AC
∴ ∠B=∠C ( )
等边对等角
C
A
B
2、等腰三角形一个底角为70°,它的顶角为______.
3、等腰三角形一个内角为70°,它的另外两个角为
__________________.
4、等腰三角形一个内角为100°,它的另外两个角为___________.
40 °
40 °,40 °
70°,40°或55°,55°
1、等腰三角形一个顶角为70°,其它两个角为_________.
55°,55°
是底边上的高,
AD垂直于BC
底边上的中线、
性质2:
等腰三角形的顶角平分线、底边上
的中线、底边上的高相互重合。
简称“等腰三角形三线合一”.
AD平分∠BAC
AD是BC的中线
顶角平分线、
A
B
D
C
观察我们刚才的探索与证明过程,你发现等腰三角形两底角相等外,你还发现了哪些等量关系?
∠1= ∠ 2
∠ADB= ∠ ADC=900
BD=CD
2
1
1、 根据等腰三角形性质定理2,在△ABC中, AB=AC时,
∵AD⊥BC,
∴∠_____ = ∠_____,____= ____.
(2) ∵AD是中线,
∴____⊥____ ,∠_____ =∠_____.
(3) ∵AD是角平分线,
∴____ ⊥____ ,_____ =_____.
A
B
C
D
BAD
CAD
CAD
BD
CD
AD
BC
BD
BAD
BC
AD
CD
2:△ ABC是等腰直角三角形 (AB=AC, ∠ BAC=90°),AD是底 边BC上的高,标出∠ B, ∠ C, ∠ BAD, ∠ DAC的度数?
B
A
C
D
答: ∠ B= ∠ C= ∠ BAD= ∠ DAC=45°
A
C
B
D
如图,是西安半坡博物馆屋顶的截面图,已经知道它的两边AB和AC是相等的.建筑工人师傅对这个建筑物做出了两个判断:
①工人师傅在测量了∠B为37°以后,并没有测量∠C ,就说∠C 的度数也是37°.
②工人师傅要加固屋顶,他们通过测量找到了横梁BC的中点D,然后在AD两点之间钉上一根木桩,他们认为木桩是垂直横梁的.
请同学们想想,工人师傅的说法对吗?请说明理由.
(学以致用)
如图,在△ ABC中,AB=AC,点D在AC上,
且BD=BC=AD。求△ ABC各角的度数。
A
B
C
D
解:∵ AB=AC BD=BC=AD
∴ ∠ABC= ∠ C= ∠ 3
∠ A= ∠1(等边对等角)
设 ∠ A=x,则
∠ 3= ∠ A+ ∠ 1=2x
从而 ∠ ABC= ∠ C= ∠ 3=2x
于是在△ ABC中,有
∠ A+ ∠ ABC+ ∠ C=x+2x+2x=1800
解得 x=360
在 △ABC中, ∠ A=360, ∠ ABC= ∠ C=720
1
2
3
一题多解
如图,点D、E在△ABC的边BC上,
且AB=AC,AD=AE,此时BD与CE有
何关系?请说明理由。
等腰三角形的性质
等边对等角
等腰三角形
三线合一
课本:P56页
第4、7题
作
业
:
