数学六年级下浙教版4.17圆柱的表面积课件 (30张)1
文档属性
| 名称 | 数学六年级下浙教版4.17圆柱的表面积课件 (30张)1 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-09 00:00:00 | ||
图片预览






文档简介
课件30张PPT。圆柱的表面积
计算下面圆的周长和面积。(1)d=6cm
(2) r=5dm周长:
面积:6×3.14=18.84(cm)(6÷2)2×3.14=28.26(cm2)周长:
面积:2×5×3.14=31.4(cm)52×3.14=78.5(cm2)要牢记下面的计算公式圆的周长
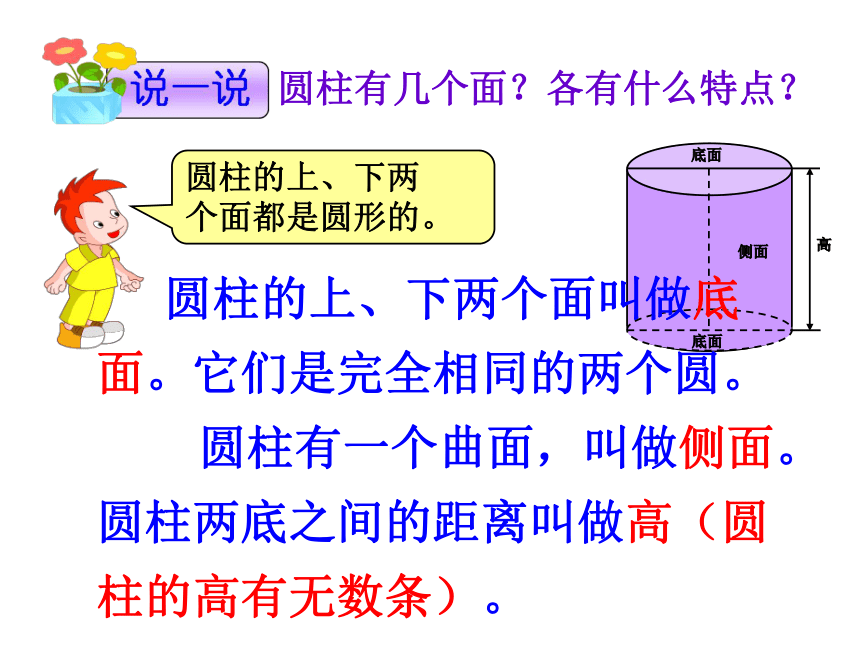
圆的面积 C=πd 或 C=2πrS=πr2圆柱有几个面?各有什么特点?圆柱的上、下两
个面都是圆形的。底面底面高侧面 圆柱的上、下两个面叫做底
面。它们是完全相同的两个圆。
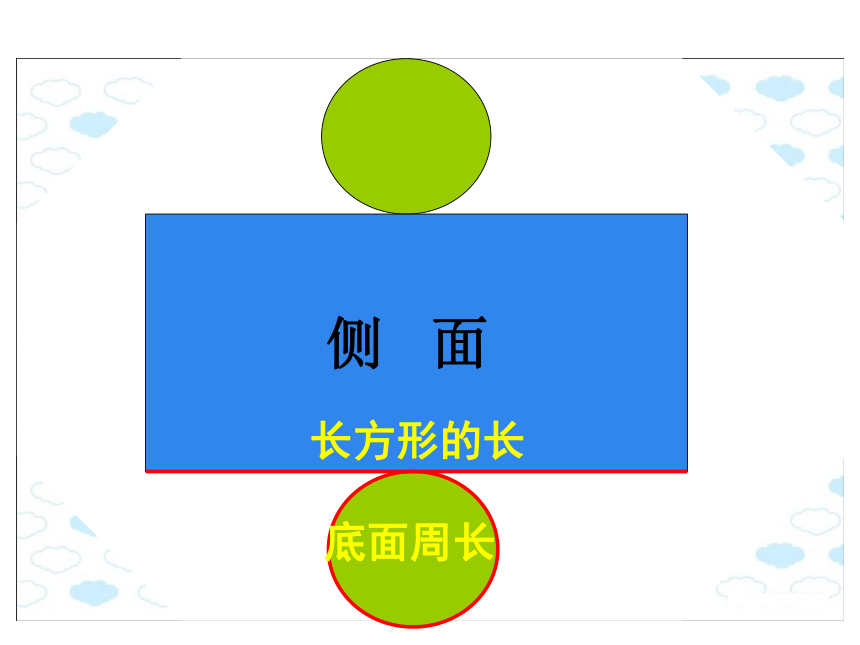
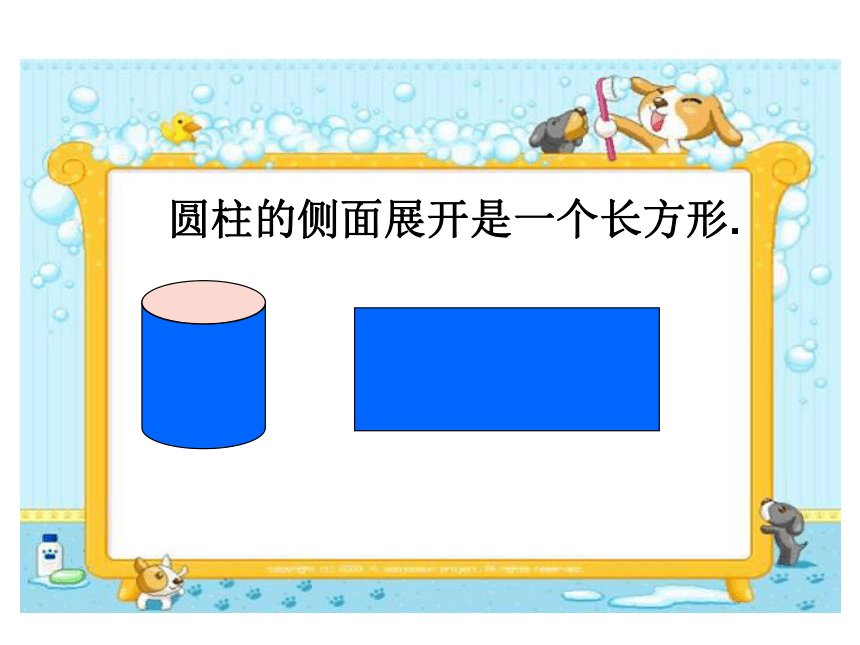
圆柱有一个曲面,叫做侧面。圆柱两底之间的距离叫做高(圆柱的高有无数条)。侧 面长方形的长底面周长圆柱的侧面展开是一个长方形.1、有两个底面:2、一个侧面:面积相等宽长高长=底面周长底面底面底面的周长底面底面底面的周长高高圆柱的侧面积=底面周长×高长方形的长=圆柱的底面周长,长方形的宽=圆柱的高。S侧=Ch圆柱的表面由上、下两个底面和一个侧面组成。 圆柱的表面积=侧面积+两个底面的面积一个圆柱茶叶筒的侧面贴着商标纸,这张商标纸的面积是多少?30(1)侧面积:2 ×3.14 ×10 ×30=1884(平方厘米)(2)底面积:3.14 ×102 =314(平方厘米)(3)表面积:1884+314 × 2=2512(平方厘米) 例2:一个圆柱的高是15厘米,底面半径是5厘米,它的表面积是多少?15(1)侧面积:2 ×3.14 ×5 ×15=471(平方厘米)(2)底面积:3.14 ×52 =78.5(平方厘米)(3)表面积:471+78.5 × 2=628(平方厘米)例3、一个没有盖的圆柱形铁皮水桶,高是24厘米,底面直径是20厘米,做这个水桶要用铁皮多少平方厘米?(得数保留整百平方厘米)明确:水桶没有盖,说明它只有一个底面。(1)水桶的侧面积:3.14 ×20 ×24=1507.2(平方厘米)(2)水桶的底面积:3.14 ×(20÷2) 2=314(平方厘米)(3)需要铁皮:1507.2+314=1821.2≈ 1900(平方厘米) 这道题使用的材料要比计算得到的结果多一些。因此,这里不能用四舍五入法取近似值。而要用进一法取近似值。帽子侧面积:3.14×20×28=1758.4(cm2)帽顶的面积:3.14×(20÷2)2 =314 (cm2)所用面料:1758.4+314=2072.4 (cm2) =2080 (cm2)
答:做这样一顶帽子至少需要用2080平方厘米面料。做一个无盖的圆柱形铁皮水桶,高是5分米。底面直径4分米,至少需要多大面积的铁皮?水桶没有盖,说明它只有一个底面。(1)水桶的侧面积:
3.14 ×4 ×5=62.8(平方分米)(2)水桶的底面积:
3.14 ×(4÷2) 2=12.56(平方分米)(3)需要铁皮:
62.8+12.56=75.36(平方分米)在解答实际问题前一定要先进行分析,看它们求的是哪部分面积,再选择解答的方法。 努力吧!1、计算下现各圆柱的表面积。(单位:厘米)222、计算下面各圆柱的表面积。①C=9.42 cm,h=5 cm。②d=8 m,h=3 m。③r=2 dm,h=6 dm。9.42×5+(9.42÷3.14÷2)×2=47.1+4.5=51.6(平方厘米)2思考题1、一个圆柱体的侧面展开是个边长9.42 cm的正方形,这个圆柱体的表面积是多少cm2?(得数保留两位小数)9.42×9.42 + 3.14×(9.42÷3.14÷2)2×2
=88.728 + 3.14×2.25×2
=102.858
≈102.86( cm2 )
2、一个圆柱体的侧面积是226.08 cm2,底面半径4 cm,它的高是多少?226.08÷(2×3.14×4)
=226.08÷25.12
=9(cm)
答:它的高是9 cm。答:这个圆柱体的表面积是102.86 cm2。3、一个圆柱,底面周长是94.2 cm,高是25 cm,求它的侧面积。5、砌一个圆柱形沼气池,底面直径是4 m,深是2 m。在池的周围与底面抹上水泥,抹水泥部分的面积是多少平方米?94.2×25=235.5(cm2)4、一个圆柱,底面直径是2 dm,高是45 dm,求它的表面积。3.14×2×45+3.14×12×2
=282.6+6.28
=288.88(dm2)3.14×4×2+3.14×22
=25.12+12.56
=37.68(m2)
答:抹水泥的面积是37.68 m2B选一选A: 6 B: 12C: 24一个圆柱形木棒,底面半径2厘米,高3厘米,沿底面直径纵剖后,表面积之和增加( )平方厘米。 如果一段圆柱形的木头,截成两截,它的表面积会有什么变化呢?
计算下面圆的周长和面积。(1)d=6cm
(2) r=5dm周长:
面积:6×3.14=18.84(cm)(6÷2)2×3.14=28.26(cm2)周长:
面积:2×5×3.14=31.4(cm)52×3.14=78.5(cm2)要牢记下面的计算公式圆的周长
圆的面积 C=πd 或 C=2πrS=πr2圆柱有几个面?各有什么特点?圆柱的上、下两
个面都是圆形的。底面底面高侧面 圆柱的上、下两个面叫做底
面。它们是完全相同的两个圆。
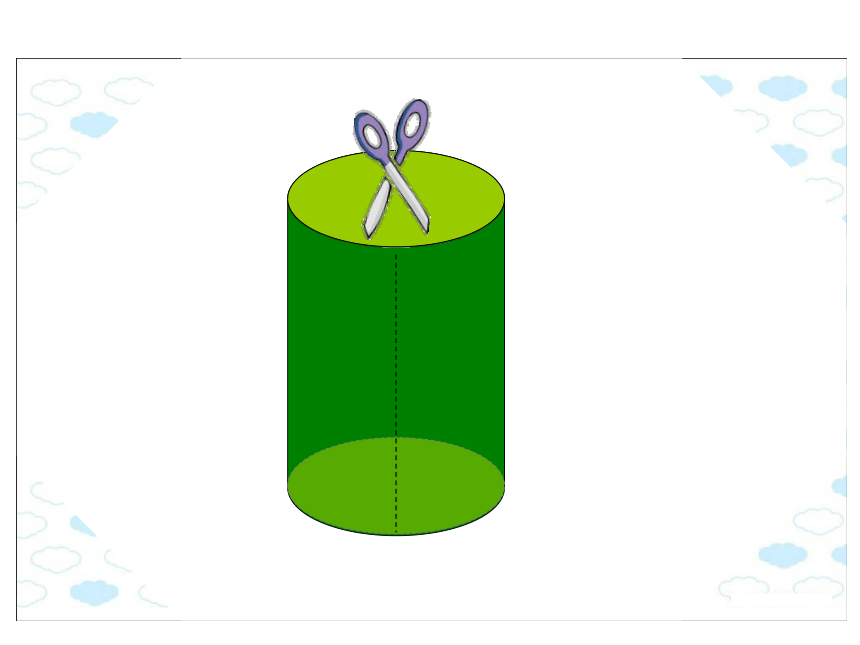
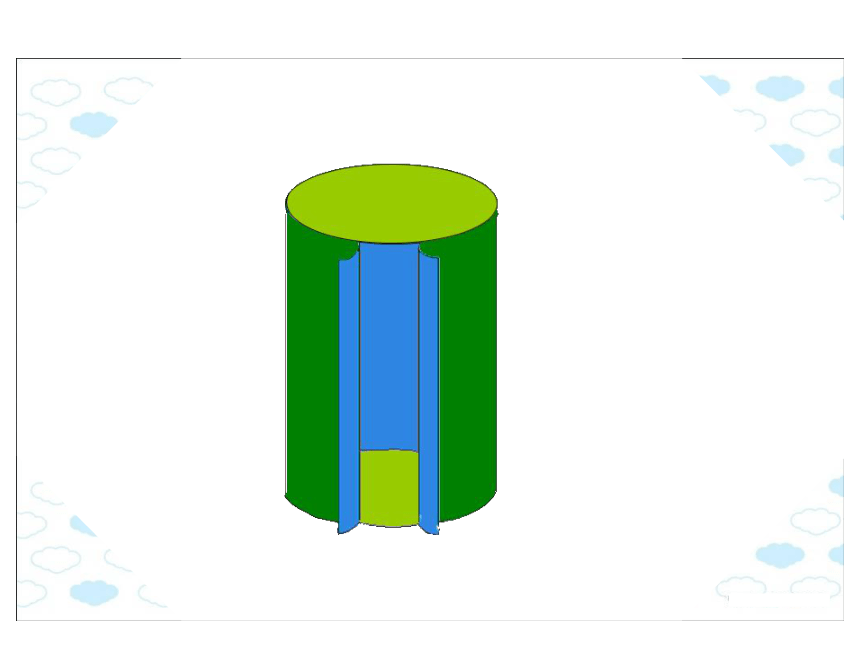
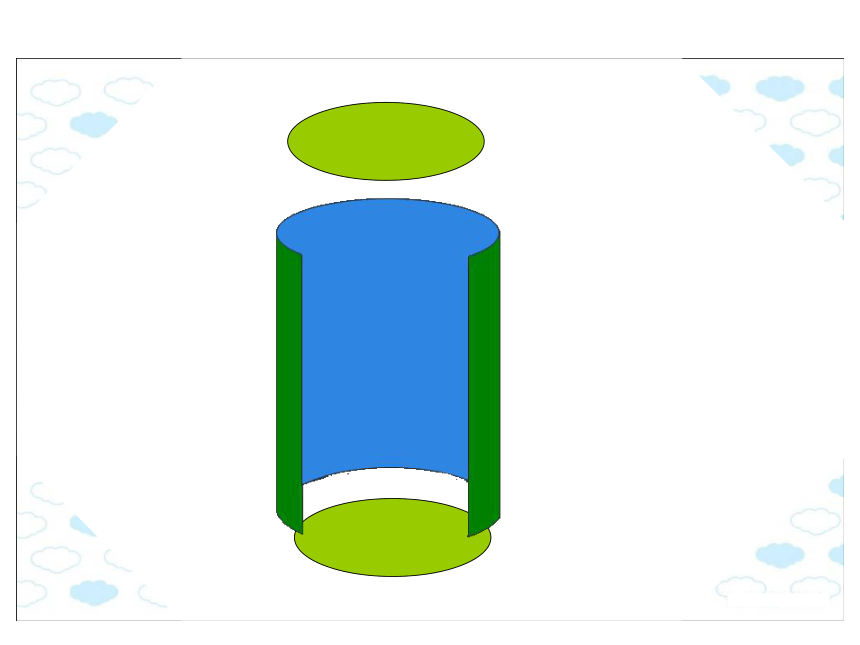
圆柱有一个曲面,叫做侧面。圆柱两底之间的距离叫做高(圆柱的高有无数条)。侧 面长方形的长底面周长圆柱的侧面展开是一个长方形.1、有两个底面:2、一个侧面:面积相等宽长高长=底面周长底面底面底面的周长底面底面底面的周长高高圆柱的侧面积=底面周长×高长方形的长=圆柱的底面周长,长方形的宽=圆柱的高。S侧=Ch圆柱的表面由上、下两个底面和一个侧面组成。 圆柱的表面积=侧面积+两个底面的面积一个圆柱茶叶筒的侧面贴着商标纸,这张商标纸的面积是多少?30(1)侧面积:2 ×3.14 ×10 ×30=1884(平方厘米)(2)底面积:3.14 ×102 =314(平方厘米)(3)表面积:1884+314 × 2=2512(平方厘米) 例2:一个圆柱的高是15厘米,底面半径是5厘米,它的表面积是多少?15(1)侧面积:2 ×3.14 ×5 ×15=471(平方厘米)(2)底面积:3.14 ×52 =78.5(平方厘米)(3)表面积:471+78.5 × 2=628(平方厘米)例3、一个没有盖的圆柱形铁皮水桶,高是24厘米,底面直径是20厘米,做这个水桶要用铁皮多少平方厘米?(得数保留整百平方厘米)明确:水桶没有盖,说明它只有一个底面。(1)水桶的侧面积:3.14 ×20 ×24=1507.2(平方厘米)(2)水桶的底面积:3.14 ×(20÷2) 2=314(平方厘米)(3)需要铁皮:1507.2+314=1821.2≈ 1900(平方厘米) 这道题使用的材料要比计算得到的结果多一些。因此,这里不能用四舍五入法取近似值。而要用进一法取近似值。帽子侧面积:3.14×20×28=1758.4(cm2)帽顶的面积:3.14×(20÷2)2 =314 (cm2)所用面料:1758.4+314=2072.4 (cm2) =2080 (cm2)
答:做这样一顶帽子至少需要用2080平方厘米面料。做一个无盖的圆柱形铁皮水桶,高是5分米。底面直径4分米,至少需要多大面积的铁皮?水桶没有盖,说明它只有一个底面。(1)水桶的侧面积:
3.14 ×4 ×5=62.8(平方分米)(2)水桶的底面积:
3.14 ×(4÷2) 2=12.56(平方分米)(3)需要铁皮:
62.8+12.56=75.36(平方分米)在解答实际问题前一定要先进行分析,看它们求的是哪部分面积,再选择解答的方法。 努力吧!1、计算下现各圆柱的表面积。(单位:厘米)222、计算下面各圆柱的表面积。①C=9.42 cm,h=5 cm。②d=8 m,h=3 m。③r=2 dm,h=6 dm。9.42×5+(9.42÷3.14÷2)×2=47.1+4.5=51.6(平方厘米)2思考题1、一个圆柱体的侧面展开是个边长9.42 cm的正方形,这个圆柱体的表面积是多少cm2?(得数保留两位小数)9.42×9.42 + 3.14×(9.42÷3.14÷2)2×2
=88.728 + 3.14×2.25×2
=102.858
≈102.86( cm2 )
2、一个圆柱体的侧面积是226.08 cm2,底面半径4 cm,它的高是多少?226.08÷(2×3.14×4)
=226.08÷25.12
=9(cm)
答:它的高是9 cm。答:这个圆柱体的表面积是102.86 cm2。3、一个圆柱,底面周长是94.2 cm,高是25 cm,求它的侧面积。5、砌一个圆柱形沼气池,底面直径是4 m,深是2 m。在池的周围与底面抹上水泥,抹水泥部分的面积是多少平方米?94.2×25=235.5(cm2)4、一个圆柱,底面直径是2 dm,高是45 dm,求它的表面积。3.14×2×45+3.14×12×2
=282.6+6.28
=288.88(dm2)3.14×4×2+3.14×22
=25.12+12.56
=37.68(m2)
答:抹水泥的面积是37.68 m2B选一选A: 6 B: 12C: 24一个圆柱形木棒,底面半径2厘米,高3厘米,沿底面直径纵剖后,表面积之和增加( )平方厘米。 如果一段圆柱形的木头,截成两截,它的表面积会有什么变化呢?
同课章节目录
- 一 比例
- 1、比例的意义与性质
- 2、正比例(一)
- 3、解比例
- 4、正比例(二)
- 5、正比例应用问题
- 6、反比例(一)
- 7、反比例(二)
- 8、反比例应用问题
- 二 比例尺
- 9、认识比例尺
- 10、比例尺的应用
- 11、方向与位置
- 四 圆柱与圆锥
- 16、圆柱与圆锥的认识
- 17、圆柱的表面积
- 18、圆柱的体积
- 19、圆锥的体积
- 五 整理与复习
- 20、整数与小数
- 21、数的整除
- 22、分数与百分数
- 23、加减运算
- 24、乘除运算
- 25、四则混合运算
- 26、代数式与方程
- 27、比与比例
- 28、应用问题
- 29、线与角
- 30、方向与位置
- 31、位置的确定
- 32、平面图形
- 33、图形的交换
- 34、立体图形
- 35、数据的整理
- 36、统计与可能性
- 总复习
