高考物理第二轮复习专题 第一讲 平衡问题(教师版)[原创][下学期]
文档属性
| 名称 | 高考物理第二轮复习专题 第一讲 平衡问题(教师版)[原创][下学期] |
|
|
| 格式 | rar | ||
| 文件大小 | 125.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2006-04-20 00:00:00 | ||
图片预览



文档简介
第一讲 平衡问题
一、典型例题
1、力学中的平衡:运动状态未发生改变,即。表现:静止或匀速直线运动
(1)在重力、弹力作用下的平衡
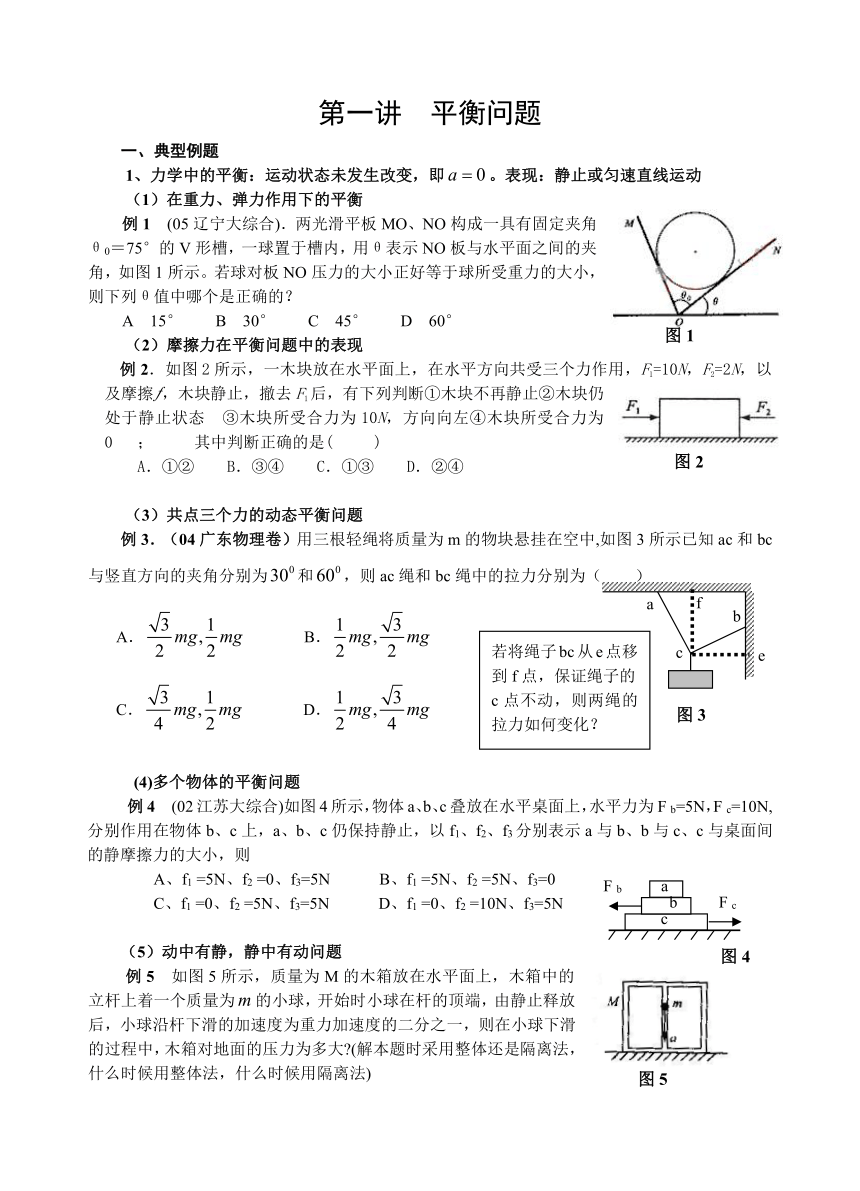
例1 (05辽宁大综合).两光滑平板MO、NO构成一具有固定夹角θ0=75°的V形槽,一球置于槽内,用θ表示NO板与水平面之间的夹角,如图1所示。若球对板NO压力的大小正好等于球所受重力的大小,则下列θ值中哪个是正确的?
A 15° B 30° C 45° D 60°
(2)摩擦力在平衡问题中的表现
例2.如图2所示,一木块放在水平面上,在水平方向共受三个力作用,F1=10N,F2=2N,以及摩擦 ,木块静止,撤去F1后,有下列判断①木块不再静止②木块仍处于静止状态 ③木块所受合力为10N,方向向左④木块所受合力为0 ; 其中判断正确的是( )
A.①② B.③④ C.①③ D.②④
(3)共点三个力的动态平衡问题
例3.(04广东物理卷)用三根轻绳将质量为m的物块悬挂在空中,如图3所示已知ac和bc与竖直方向的夹角分别为和,则ac绳和bc绳中的拉力分别为( )
A. B.
C. D.
(4)多个物体的平衡问题
例4 (02江苏大综合)如图4所示,物体a、b、c叠放在水平桌面上,水平力为F b=5N,F c=10N,分别作用在物体b、c上,a、b、c仍保持静止,以f1、f2、f3分别表示a与b、b与c、c与桌面间的静摩擦力的大小,则
A、f1 =5N、f2 =0、f3=5N B、f1 =5N、f2 =5N、f3=0
C、f1 =0、f2 =5N、f3=5N D、f1 =0、f2 =10N、f3=5N
(5)动中有静,静中有动问题
例5 如图5所示,质量为M的木箱放在水平面上,木箱中的立杆上着一个质量为的小球,开始时小球在杆的顶端,由静止释放后,小球沿杆下滑的加速度为重力加速度的二分之一,则在小球下滑的过程中,木箱对地面的压力为多大 (解本题时采用整体还是隔离法,什么时候用整体法,什么时候用隔离法)
2电磁学的平衡问题
例6 一金属球,原来不带电。现沿球的直径的延长线放置一均匀带电的细杆MN,如图6所示。金属球上感应电荷产生的电场在球内直径上、、三点的场强大小分别为、、,三者相比,
A、最大 B、最大 C、最大 D、==
例7 如图7所示,匀强电场方向向右,匀强磁场方向垂直于纸面向里,一质量为带电量为q的微粒以速度与磁场垂直、与电场成45 角射入复合场中,恰能做匀速直线运动,求电场强度E的大小?磁感强度B的大小?
例8 (2005年天津理综卷) 23.(16分)图8中MN和PQ为竖直方向的两平行长直金属导轨,间距l为0.40m,电阻不计。导轨所在平面与磁感应强度B为0.50T的匀强磁场垂直。质量m为6.0×10-3kg、电阻为1.0Ω的金属杆ab始终垂直于导轨,并与其保持光滑接触。导轨两端分别接有滑动变阻器和阻值为3.0Ω的电阻R1。当杆ab达到稳定状态时以速率v匀速下滑,整个电路消耗的电功率P为0.27W,重力加速度取10m/s2,试求速率v和滑动变阻器接入电路部分的阻值R2。
(此题可联系动态收尾平衡问题,比如说雨滴的下落过程等)
3、原子物理中的平衡问题
例9 (03年广东物理卷) 4.铀裂变的产物之一氪90()是不稳定的,它经过一系列衰变最终成为稳定的锆90(),这些衰变是
A.1次衰变,6次衰变 B.4 次衰变
C.2次衰变 D.2次衰变,2次衰变
二、课后同步练习
1、(03全国理综)如图1—1所示,一个半球形的碗放在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的。一根细线跨在碗口上,线的两端分别系有质量为m1和m2的小球,当它们处于平衡状态时,质量为m1的小球与O点的连线与水平线的夹角为α=60°。两小球的质量比m2/m1为( )
A. B. C. D.
2、如图1-2所示,固定在水平面上的光滑半球,球心0的正上方固定 一个小定滑轮,细线一端拴一小球,置于半球面上的A点,另一端绕过定滑轮,如图,现缓慢的将小球从A点拉到B点,则此过程中,小球对半球的压力大小FN,细线的拉力大小FT的变化情况是:
A、FN变大,FT不变 B、FN变小,FT变大
C、FN不变,FT变小 D、FN变大,FT变小
3、(05年天津理)如图1-3所示,表面粗糙的固定斜面顶端安有滑轮,两物块P、Q用轻绳连接并跨过滑轮(不计滑轮的质量和摩擦),P悬于空中,Q放在斜面上,均处于静止状态。当用水平向左的恒力推Q时,P、Q仍静止不动,则
A Q受到的摩擦力一定变小
B Q受到的摩擦力一定变大
C 轻绳上拉力一定变小
D 轻绳上拉力一定不变
4、(02全国理综)有三根长度皆为l=1.00 m的不可伸长的绝缘轻线,其中两根的一端固定在天花板上的 O点,另一端分别挂有质量皆为m=1.00×10-2 kg的带电小球A和B,它们的电量分别为一q和+q,q=1.00×10-7C。A、B之间用第三根线连接起来。空间中存在大小为E=1.00×106N/C的匀强电场,场强方向沿水平向右,平衡时 A、B球的位置如图1—4所示。现将O、B之间的线烧断,由于有空气阻力,A、B球最后会达到新的平衡位置。求最后两球的机械能与电势能的总和与烧断前相比改变了多少。(不计两带电小球间相互作用的静电力)
5、(98上海物理)有一个直角支架AOB,AO水平放置,表面粗糙,OB竖直向下,表面光滑。AO上套有小环P,OB套有小环Q,两环质量均为m,两环间由一根质量可忽略、不可伸长的细绳相连,并在某一位置平衡,如图1—5所示。现将P环向左移一小段距离,两环再次达到平衡,那么将P环移动后的平衡状态和原来的平衡状态比较,AO杆对P环的支持力N和细绳上拉力T的变化情况是( )
A.N不变,T变大 B.N不变,T变小
C.N变大,T变大 D.N变大,T变小
6、(00上海物理)(风洞实验中可产生水平方向的,大小可调节的风力。现将一套有小球的细直杆放入风洞实验室,如图1—6。小球孔径略大于细杆直径。
(1)当杆在水平方向上固定时,调节风力的大小,使小球在杆上作匀速运动,这时小球所受的风力为小球所受重力的0.5倍,求小球与杆间的动摩擦因数。
(2)保持小球所受风力不变,使杆与水平方向间夹角为370并固定,则小球从静止出发在细杆上滑下距离S所需时间为多少?(sin370=0.6,cos370=0.8)
7、(2001全国物理)如图1—7所示,质量为m、横截面为直角三角形的物块ABC,∠ABC=a,AB边靠在竖直墙面上,F是垂直于斜面BC的推力,现物块静止不动,则摩擦力的大小为 。
8、(2003江苏物理)当物体从高空下落时,空气阻力随速度的增大而增大,因此经过一段距离后将匀速下落,这个速度称为此物体下落的终极速度。已知球形物体速度不大时所受的空气阻力正比于速度v且正比于球半径r,即阻力f=krv,k是比例系数。对于常温下的空气,比例系数k=3.4×10-4Ns/m2。已知水的密度ρ=1.0×103kg/m3,取重力加速度g=10m/s2。试求半径r=0.10mm的球形雨滴在无风情况下的终极速度vr。(结果取两位数字)
9、(03辽宁大综合)如图1—9所示,一质量为M的楔形木块放在水平桌面上,它的顶角为90°,两底角为α和β;a、b为两个位于斜面上质量均为m的小木块。已知所有接触面都是光滑的。现发现a、b沿斜面下滑,而楔形木块静止不动,这时楔形木块对水平桌面的压力等于( )
A.Mg+mg C.Mg+mg(sinα+sinβ)
B.Mg+2mg D.Mg+mg(cosα+cosβ)
10、如图所示a、b、c为三个物块,M、N为两个轻质弹簧,
R为跨过光滑定滑轮的轻绳,它们连接如图1-10并处于平衡状态.
(1)有可能N处于拉伸状态而M处于压缩状态
(2)有可能N处于压缩状态而M处于拉伸状态
(3)有可能N处于不伸不缩状态而M处于拉伸状态
(4)有可能N处于拉伸状态而M处于不伸不缩状态
A.(1)(2) B.(2)(3) C.(3)(4) D.(l)(4)
11、两块金属a.b平行放置,板间存在与匀强电场正交的匀强磁场,假设电场.磁场只存在于两板间的空间区域。一束电子以一定的初速度v0从两极板中间,沿垂直于电场.磁场的方向射入场中,无偏转地通过场区,如图1-11所示。已知板长l=10cm,两板间距d=3.0cm,两板间电势差U=150V,v0=2.0×107m/s。求:
(1)求磁感应强度B的大小;
(2)若撤去磁场,求电子穿过电场时偏离入射方向的距离,以及电子通过场区后动能增加多少?(电子所带电荷量的大小与其质量之比,电子电荷量的大小e=1.60×10—19C)
平衡问题答案
一、典型例题
例1. B 例2. D 例3. A 例4.C
例5. 如图所示,质量为M的木箱放在水平面上,木箱中的立杆上着一个质量为的小球,开始时小球在杆的顶端,由静止释放后,小球沿杆下滑的加速度为重力加速度的二分之一,则在小球下滑的过程中,木箱对地面的压力为。因为球加速下滑时,杆受向上的摩擦力根据第二定律有,所以。对木箱进行受力分析有:重力、地面支持力N、及球对杆向下的摩擦力。由平衡条件有。
例6.D
例7. 解析 由于带电粒子所受洛仑兹力与垂直,电场力方向与电场线平行,知粒子必须还受重力才能做匀速直线运动。假设粒子带负电受电场力水平向左,则它受洛仑兹力就应斜向右下与垂直,这样粒子不能做匀速直线运动,所以粒子应带正电,画出受力分析图根据合外力为零可得,
(1) (2)
由(1)式得,由(1),(2)得
例8. 由能量守恒定律得:mgv=P
代入数据得:v=4.5m/s 又 E=BLv
设电阻R与R的并联电阻为R,ab棒的电阻为r,有
P=IE
代入数据得:=6.0Ω
例9. B
二、课后同步练习
1. A 2. C 3. D
4. 右图中虚线表示A、B球原来的平衡位置,实线表示烧断后重新达到平衡的位置,其中α、β分别表示细线OA、AB与竖直方向的夹角。
A球受力如右图所示:重力mg,竖直向下;电场力qE,水平向左;细线OA对A的拉力T1,方向如图;细线AB对A的拉力T2,方向如图。由平衡条件
T1sinα+T2sinβ=qE ①
T2cosα=mg+T2 cosβ ②
B球受力如右图所示:重力mg,竖直向下;电场力qE,水平向右;细线AB对B的拉力T2,方向如图。由平衡条件
T2sinβ=qE ③
T2cosβ=mg ④
联立以上各式并代入数据,得
α=0 ⑤
β=45° ⑥
由此可知,A、B球重新达到平衡的位置如右图所示。与原来位置相比,A球的重力势能减少了
EA=mgl(1-sin60°) ⑦
B球的重力势能减少了
EB=mgl(1-sin60°+cos45°) ⑧
A球的电势能增加了
WA=qElcos60° ⑨
B球的电势能减少了
WB=qEl(sin45°-sin30°) ⑩
两种势能总和减少了
W=WB-WA+EA+EB
代入数据解得
W=6.8×10-2J
5. B 解法一:设PQ与OA的夹角为,则对P有:mg+Fsin=FN,对Q有:Fsin=mg,所以FN=2mg,F=mg/sin。正确选项为B。
解法二:将P、Q两环看作一个整体,在竖直方向上两环只受重力和OA杆对P环的支持力FN,所以FN=2mg,即FN不变。
以Q环为研究对象,绳的拉力的竖直分力等于Q环的重力,即Fsin=mg,所以F越来越小。
说明:在解决物体之间的相互作用时,常常采用隔离法和整体法。若不涉及物体之间的作用可用整体法,若要求物体之间的相互作用需再用隔离法。
6. (1)设小球所受的风力为F,小球质量为
(2)设杆对小球的支持力为N,摩擦力为
沿杆方向
垂直于杆方向
可解得
7. 如图所示,物块ABC受到重力、墙的支持力、摩擦力及推力四个力而平衡,竖直方向上mg+Fsinα=f.
故摩擦力大小为mg+Fsinα.
8. 雨滴下落时受两个力作用:重力,方向向下;空气阻力,方向向上,当雨滴达到终极速度后,加速度为零,二力平衡,用表示雨滴质量,有
① ② 由①②得终极速度③
代入数值得=1.2m/s .
9. A 10. D
11. (1)电子进入正交的电磁场不发生偏转,则满足
(2)设电子通过场区偏转的距离为y1
P
若将绳子bc从e点移到f点,保证绳子的c点不动,则两绳的拉力如何变化?
f
e
c
b
a
图1-1
图1-2
图8
v
B
Q
P
N
M
b
a
l
R2
图2
图1
R1
B
E
× × × × × ×
× × × × × ×
图7
图6
图5
图4
F c
F b
c
b
a
图3
图1-5
图1-4
图1-3
Q
A
O
B
P
Q
图1-6
图1-7
图1-9
图1-10
图1-11
一、典型例题
1、力学中的平衡:运动状态未发生改变,即。表现:静止或匀速直线运动
(1)在重力、弹力作用下的平衡
例1 (05辽宁大综合).两光滑平板MO、NO构成一具有固定夹角θ0=75°的V形槽,一球置于槽内,用θ表示NO板与水平面之间的夹角,如图1所示。若球对板NO压力的大小正好等于球所受重力的大小,则下列θ值中哪个是正确的?
A 15° B 30° C 45° D 60°
(2)摩擦力在平衡问题中的表现
例2.如图2所示,一木块放在水平面上,在水平方向共受三个力作用,F1=10N,F2=2N,以及摩擦 ,木块静止,撤去F1后,有下列判断①木块不再静止②木块仍处于静止状态 ③木块所受合力为10N,方向向左④木块所受合力为0 ; 其中判断正确的是( )
A.①② B.③④ C.①③ D.②④
(3)共点三个力的动态平衡问题
例3.(04广东物理卷)用三根轻绳将质量为m的物块悬挂在空中,如图3所示已知ac和bc与竖直方向的夹角分别为和,则ac绳和bc绳中的拉力分别为( )
A. B.
C. D.
(4)多个物体的平衡问题
例4 (02江苏大综合)如图4所示,物体a、b、c叠放在水平桌面上,水平力为F b=5N,F c=10N,分别作用在物体b、c上,a、b、c仍保持静止,以f1、f2、f3分别表示a与b、b与c、c与桌面间的静摩擦力的大小,则
A、f1 =5N、f2 =0、f3=5N B、f1 =5N、f2 =5N、f3=0
C、f1 =0、f2 =5N、f3=5N D、f1 =0、f2 =10N、f3=5N
(5)动中有静,静中有动问题
例5 如图5所示,质量为M的木箱放在水平面上,木箱中的立杆上着一个质量为的小球,开始时小球在杆的顶端,由静止释放后,小球沿杆下滑的加速度为重力加速度的二分之一,则在小球下滑的过程中,木箱对地面的压力为多大 (解本题时采用整体还是隔离法,什么时候用整体法,什么时候用隔离法)
2电磁学的平衡问题
例6 一金属球,原来不带电。现沿球的直径的延长线放置一均匀带电的细杆MN,如图6所示。金属球上感应电荷产生的电场在球内直径上、、三点的场强大小分别为、、,三者相比,
A、最大 B、最大 C、最大 D、==
例7 如图7所示,匀强电场方向向右,匀强磁场方向垂直于纸面向里,一质量为带电量为q的微粒以速度与磁场垂直、与电场成45 角射入复合场中,恰能做匀速直线运动,求电场强度E的大小?磁感强度B的大小?
例8 (2005年天津理综卷) 23.(16分)图8中MN和PQ为竖直方向的两平行长直金属导轨,间距l为0.40m,电阻不计。导轨所在平面与磁感应强度B为0.50T的匀强磁场垂直。质量m为6.0×10-3kg、电阻为1.0Ω的金属杆ab始终垂直于导轨,并与其保持光滑接触。导轨两端分别接有滑动变阻器和阻值为3.0Ω的电阻R1。当杆ab达到稳定状态时以速率v匀速下滑,整个电路消耗的电功率P为0.27W,重力加速度取10m/s2,试求速率v和滑动变阻器接入电路部分的阻值R2。
(此题可联系动态收尾平衡问题,比如说雨滴的下落过程等)
3、原子物理中的平衡问题
例9 (03年广东物理卷) 4.铀裂变的产物之一氪90()是不稳定的,它经过一系列衰变最终成为稳定的锆90(),这些衰变是
A.1次衰变,6次衰变 B.4 次衰变
C.2次衰变 D.2次衰变,2次衰变
二、课后同步练习
1、(03全国理综)如图1—1所示,一个半球形的碗放在桌面上,碗口水平,O点为其球心,碗的内表面及碗口是光滑的。一根细线跨在碗口上,线的两端分别系有质量为m1和m2的小球,当它们处于平衡状态时,质量为m1的小球与O点的连线与水平线的夹角为α=60°。两小球的质量比m2/m1为( )
A. B. C. D.
2、如图1-2所示,固定在水平面上的光滑半球,球心0的正上方固定 一个小定滑轮,细线一端拴一小球,置于半球面上的A点,另一端绕过定滑轮,如图,现缓慢的将小球从A点拉到B点,则此过程中,小球对半球的压力大小FN,细线的拉力大小FT的变化情况是:
A、FN变大,FT不变 B、FN变小,FT变大
C、FN不变,FT变小 D、FN变大,FT变小
3、(05年天津理)如图1-3所示,表面粗糙的固定斜面顶端安有滑轮,两物块P、Q用轻绳连接并跨过滑轮(不计滑轮的质量和摩擦),P悬于空中,Q放在斜面上,均处于静止状态。当用水平向左的恒力推Q时,P、Q仍静止不动,则
A Q受到的摩擦力一定变小
B Q受到的摩擦力一定变大
C 轻绳上拉力一定变小
D 轻绳上拉力一定不变
4、(02全国理综)有三根长度皆为l=1.00 m的不可伸长的绝缘轻线,其中两根的一端固定在天花板上的 O点,另一端分别挂有质量皆为m=1.00×10-2 kg的带电小球A和B,它们的电量分别为一q和+q,q=1.00×10-7C。A、B之间用第三根线连接起来。空间中存在大小为E=1.00×106N/C的匀强电场,场强方向沿水平向右,平衡时 A、B球的位置如图1—4所示。现将O、B之间的线烧断,由于有空气阻力,A、B球最后会达到新的平衡位置。求最后两球的机械能与电势能的总和与烧断前相比改变了多少。(不计两带电小球间相互作用的静电力)
5、(98上海物理)有一个直角支架AOB,AO水平放置,表面粗糙,OB竖直向下,表面光滑。AO上套有小环P,OB套有小环Q,两环质量均为m,两环间由一根质量可忽略、不可伸长的细绳相连,并在某一位置平衡,如图1—5所示。现将P环向左移一小段距离,两环再次达到平衡,那么将P环移动后的平衡状态和原来的平衡状态比较,AO杆对P环的支持力N和细绳上拉力T的变化情况是( )
A.N不变,T变大 B.N不变,T变小
C.N变大,T变大 D.N变大,T变小
6、(00上海物理)(风洞实验中可产生水平方向的,大小可调节的风力。现将一套有小球的细直杆放入风洞实验室,如图1—6。小球孔径略大于细杆直径。
(1)当杆在水平方向上固定时,调节风力的大小,使小球在杆上作匀速运动,这时小球所受的风力为小球所受重力的0.5倍,求小球与杆间的动摩擦因数。
(2)保持小球所受风力不变,使杆与水平方向间夹角为370并固定,则小球从静止出发在细杆上滑下距离S所需时间为多少?(sin370=0.6,cos370=0.8)
7、(2001全国物理)如图1—7所示,质量为m、横截面为直角三角形的物块ABC,∠ABC=a,AB边靠在竖直墙面上,F是垂直于斜面BC的推力,现物块静止不动,则摩擦力的大小为 。
8、(2003江苏物理)当物体从高空下落时,空气阻力随速度的增大而增大,因此经过一段距离后将匀速下落,这个速度称为此物体下落的终极速度。已知球形物体速度不大时所受的空气阻力正比于速度v且正比于球半径r,即阻力f=krv,k是比例系数。对于常温下的空气,比例系数k=3.4×10-4Ns/m2。已知水的密度ρ=1.0×103kg/m3,取重力加速度g=10m/s2。试求半径r=0.10mm的球形雨滴在无风情况下的终极速度vr。(结果取两位数字)
9、(03辽宁大综合)如图1—9所示,一质量为M的楔形木块放在水平桌面上,它的顶角为90°,两底角为α和β;a、b为两个位于斜面上质量均为m的小木块。已知所有接触面都是光滑的。现发现a、b沿斜面下滑,而楔形木块静止不动,这时楔形木块对水平桌面的压力等于( )
A.Mg+mg C.Mg+mg(sinα+sinβ)
B.Mg+2mg D.Mg+mg(cosα+cosβ)
10、如图所示a、b、c为三个物块,M、N为两个轻质弹簧,
R为跨过光滑定滑轮的轻绳,它们连接如图1-10并处于平衡状态.
(1)有可能N处于拉伸状态而M处于压缩状态
(2)有可能N处于压缩状态而M处于拉伸状态
(3)有可能N处于不伸不缩状态而M处于拉伸状态
(4)有可能N处于拉伸状态而M处于不伸不缩状态
A.(1)(2) B.(2)(3) C.(3)(4) D.(l)(4)
11、两块金属a.b平行放置,板间存在与匀强电场正交的匀强磁场,假设电场.磁场只存在于两板间的空间区域。一束电子以一定的初速度v0从两极板中间,沿垂直于电场.磁场的方向射入场中,无偏转地通过场区,如图1-11所示。已知板长l=10cm,两板间距d=3.0cm,两板间电势差U=150V,v0=2.0×107m/s。求:
(1)求磁感应强度B的大小;
(2)若撤去磁场,求电子穿过电场时偏离入射方向的距离,以及电子通过场区后动能增加多少?(电子所带电荷量的大小与其质量之比,电子电荷量的大小e=1.60×10—19C)
平衡问题答案
一、典型例题
例1. B 例2. D 例3. A 例4.C
例5. 如图所示,质量为M的木箱放在水平面上,木箱中的立杆上着一个质量为的小球,开始时小球在杆的顶端,由静止释放后,小球沿杆下滑的加速度为重力加速度的二分之一,则在小球下滑的过程中,木箱对地面的压力为。因为球加速下滑时,杆受向上的摩擦力根据第二定律有,所以。对木箱进行受力分析有:重力、地面支持力N、及球对杆向下的摩擦力。由平衡条件有。
例6.D
例7. 解析 由于带电粒子所受洛仑兹力与垂直,电场力方向与电场线平行,知粒子必须还受重力才能做匀速直线运动。假设粒子带负电受电场力水平向左,则它受洛仑兹力就应斜向右下与垂直,这样粒子不能做匀速直线运动,所以粒子应带正电,画出受力分析图根据合外力为零可得,
(1) (2)
由(1)式得,由(1),(2)得
例8. 由能量守恒定律得:mgv=P
代入数据得:v=4.5m/s 又 E=BLv
设电阻R与R的并联电阻为R,ab棒的电阻为r,有
P=IE
代入数据得:=6.0Ω
例9. B
二、课后同步练习
1. A 2. C 3. D
4. 右图中虚线表示A、B球原来的平衡位置,实线表示烧断后重新达到平衡的位置,其中α、β分别表示细线OA、AB与竖直方向的夹角。
A球受力如右图所示:重力mg,竖直向下;电场力qE,水平向左;细线OA对A的拉力T1,方向如图;细线AB对A的拉力T2,方向如图。由平衡条件
T1sinα+T2sinβ=qE ①
T2cosα=mg+T2 cosβ ②
B球受力如右图所示:重力mg,竖直向下;电场力qE,水平向右;细线AB对B的拉力T2,方向如图。由平衡条件
T2sinβ=qE ③
T2cosβ=mg ④
联立以上各式并代入数据,得
α=0 ⑤
β=45° ⑥
由此可知,A、B球重新达到平衡的位置如右图所示。与原来位置相比,A球的重力势能减少了
EA=mgl(1-sin60°) ⑦
B球的重力势能减少了
EB=mgl(1-sin60°+cos45°) ⑧
A球的电势能增加了
WA=qElcos60° ⑨
B球的电势能减少了
WB=qEl(sin45°-sin30°) ⑩
两种势能总和减少了
W=WB-WA+EA+EB
代入数据解得
W=6.8×10-2J
5. B 解法一:设PQ与OA的夹角为,则对P有:mg+Fsin=FN,对Q有:Fsin=mg,所以FN=2mg,F=mg/sin。正确选项为B。
解法二:将P、Q两环看作一个整体,在竖直方向上两环只受重力和OA杆对P环的支持力FN,所以FN=2mg,即FN不变。
以Q环为研究对象,绳的拉力的竖直分力等于Q环的重力,即Fsin=mg,所以F越来越小。
说明:在解决物体之间的相互作用时,常常采用隔离法和整体法。若不涉及物体之间的作用可用整体法,若要求物体之间的相互作用需再用隔离法。
6. (1)设小球所受的风力为F,小球质量为
(2)设杆对小球的支持力为N,摩擦力为
沿杆方向
垂直于杆方向
可解得
7. 如图所示,物块ABC受到重力、墙的支持力、摩擦力及推力四个力而平衡,竖直方向上mg+Fsinα=f.
故摩擦力大小为mg+Fsinα.
8. 雨滴下落时受两个力作用:重力,方向向下;空气阻力,方向向上,当雨滴达到终极速度后,加速度为零,二力平衡,用表示雨滴质量,有
① ② 由①②得终极速度③
代入数值得=1.2m/s .
9. A 10. D
11. (1)电子进入正交的电磁场不发生偏转,则满足
(2)设电子通过场区偏转的距离为y1
P
若将绳子bc从e点移到f点,保证绳子的c点不动,则两绳的拉力如何变化?
f
e
c
b
a
图1-1
图1-2
图8
v
B
Q
P
N
M
b
a
l
R2
图2
图1
R1
B
E
× × × × × ×
× × × × × ×
图7
图6
图5
图4
F c
F b
c
b
a
图3
图1-5
图1-4
图1-3
Q
A
O
B
P
Q
图1-6
图1-7
图1-9
图1-10
图1-11
同课章节目录
