6.3 三角形的中位线同步练习

21世纪教育网 –中小学教育资源及组卷应用平台
６．３ 三角形的中位线同步练习
　班级__________姓名____________总分___________
本节应掌握和应用的知识点
１．连接三角形两边中点的线段叫做三角形的中位线．
２．三角形中位线定理:三角形的中位线平行于第三边且等于第三边的一半 ．
基础知识和能力拓展精练
一、选择题
1．△ABC中，D、E分别是AB、AC边上的中点，若BC=8，则DE等于（ ）
A.5 B.4 C.3 D.2
2．三角形的三条中位线长分别为3cm，4cm，6cm，则原三角形的周长为( )
A. 6. 5cm B. 34cm C.26cm D. 52cm
3．如图，在四边形ABCD 中，AB=CD，M，N，P分别AD，BC，BD的中点，若∠MPN=130°，则∠NMP=（ ）
A. 25° B. 30° C. 35° D. 50°
4．如图所示，已知点E、F分别是△ABC中AC、AB边的中点，BE、CF相交于点G，FG=3，则CF的长为（ ）
A. 4 B. 4.5 C. 6 D. 9
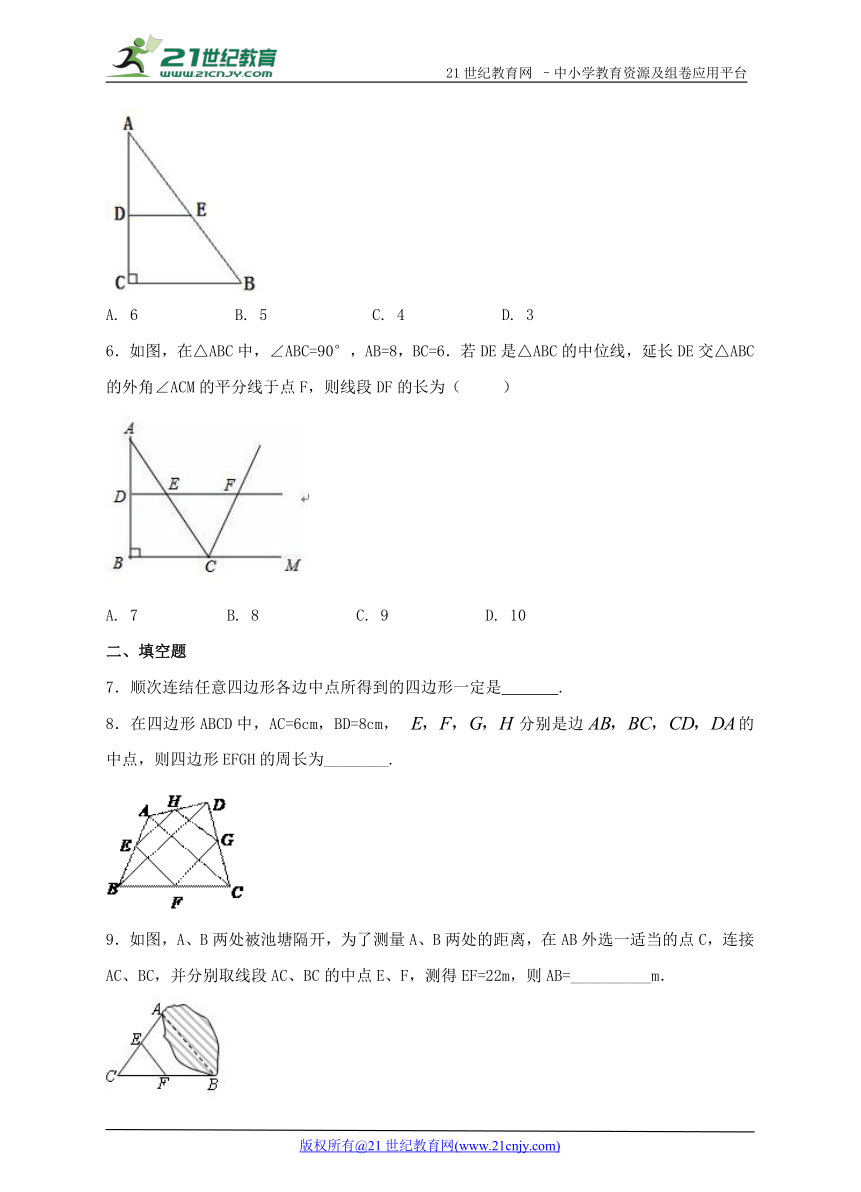
5．如图，在△ABC中，∠ACB=90°，AC=8，AB=10. DE垂直平分AC交AB于点E，则DE的长为（ ）
A. 6 B. 5 C. 4 D. 3
6．如图，在△ABC中，∠ABC=90°，AB=8，BC=6．若DE是△ABC的中位线，延长DE交△ABC的外角∠ACM的平分线于点F，则线段DF的长为（　 　）
A. 7 B. 8 C. 9 D. 10
二、填空题
7．顺次连结任意四边形各边中点所得到的四边形一定是 .
8．在四边形ABCD中，AC=6cm，BD=8cm， 分别是边的中点，则四边形EFGH的周长为________.
9．如图，A、B两处被池塘隔开，为了测量A、B两处的距离，在AB外选一适当的点C，连接AC、BC，并分别取线段AC、BC的中点E、F，测得EF=22m，则AB=__________m．
10．在△ABC中，点D、E分别是边AB、AC的中点，那么△ADE的面积与△ABC的面积的比是______.
11．如图，D是△ABC内一点，BD⊥CD，AD＝6，BD＝4，CD＝3，E、F、G、H分别是AB、AC、CD、BD的中点，则四边形EFGH的周长是____________.
12．如图，△ABC的周长为64，E、F、G分别为AB、AC、BC的中点，A′、B′、C′分别为EF、EG、GF的中点，△A′B′C′的周长为_________．如果△ABC、△EFG、△A′B′C′分别为第1个、第2个、第3个三角形，按照上述方法继续作三角形，那么第n个三角形的周长是__________________．
三、解答题
13．如图，在△ABC中，AD⊥BC于点D，E，F，G分别是BC，AC，AB的中点. 若AB=BC=3DE=12，求四边形DEFG的周长.
14．已知：△ABC的中线BD、CE交于点O，F、G分别是OB、OC的中点．求证：四边形DEFG是平行四边形．
15．如图，AD是∠BAC的外角平分线，CD⊥AD于点D，E是BC的中点.求证：DE= (AB+AC).
16．已知：如图，在四边形ABCD中，AD＝BC，E、F分别是DC、AB边的中点，FE的延长线分别与AD、BC的延长线交于H、G点．求证：∠AHF＝∠BGF．
17．已知：如图，△ABC中，D是BC边的中点，AE平分∠BAC，BE⊥AE于E点，若AB＝5，AC＝7，求ED．
18如图在△ABC中，D、E分别为AB、AC上的点，且BD＝CE，M、N分别是BE、CD的中点．过MN的直线交AB于P，交AC于Q，线段AP、AQ相等吗 为什么
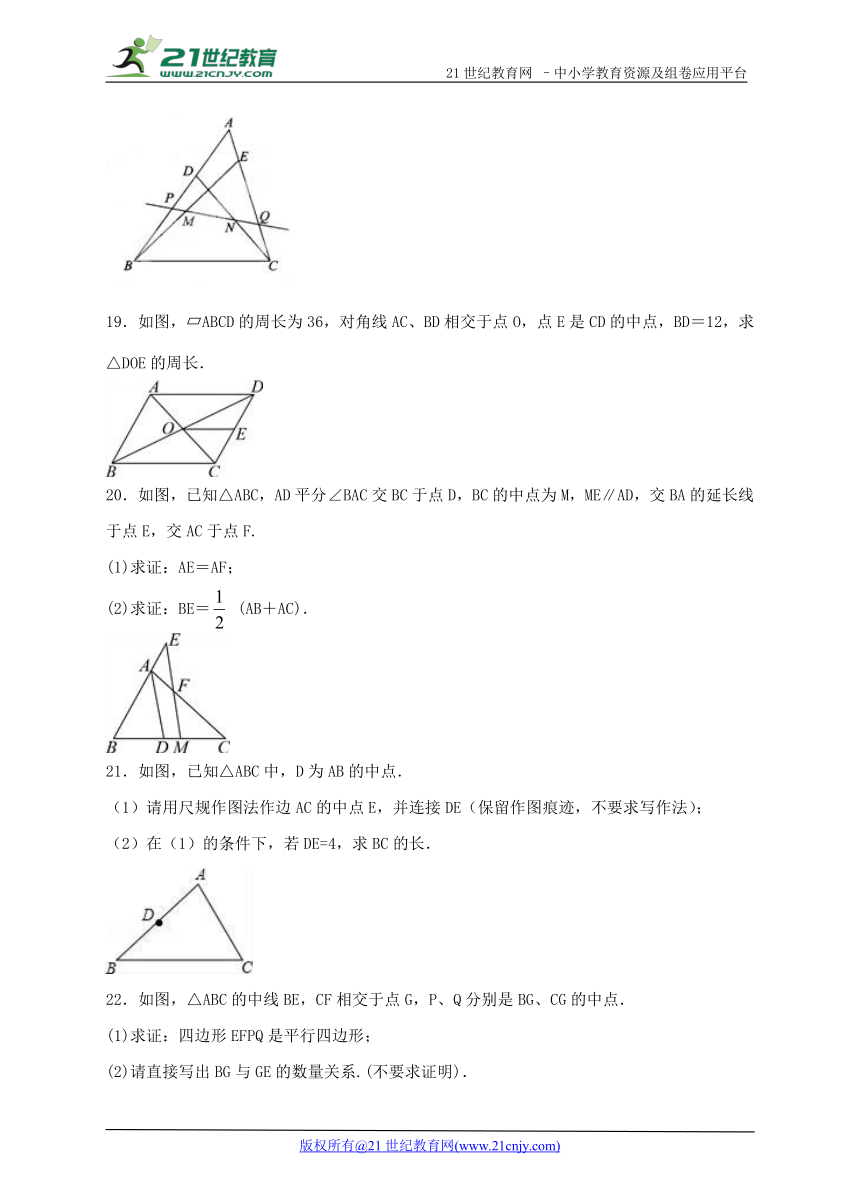
19．如图， ABCD的周长为36，对角线AC、BD相交于点O，点E是CD的中点，BD＝12，求△DOE的周长．
20．如图，已知△ABC，AD平分∠BAC交BC于点D，BC的中点为M，ME∥AD，交BA的延长线于点E，交AC于点F.
(1)求证：AE＝AF；
(2)求证：BE＝ EMBED Equation.DSMT4 (AB＋AC)．
21．如图，已知△ABC中，D为AB的中点．
（1）请用尺规作图法作边AC的中点E，并连接DE（保留作图痕迹，不要求写作法）；
（2）在（1）的条件下，若DE=4，求BC的长．
22．如图，△ABC的中线BE，CF相交于点G，P、Q分别是BG、CG的中点．
(1)求证：四边形EFPQ是平行四边形；
(2)请直接写出BG与GE的数量关系.(不要求证明)．
23．如图，AC、BD是四边形ABCD的对角线，E、F分别是AD、BC的中点，M、N分别是BD、AC的中点．
求证：EF与MN互相平分．
24．如图，在四边形ABCD中，∠ABC＝90°，AC＝AD，M、N分别为AC、CD的中点，连接BM、MN、BN.
(1)求证：BM＝MN；
(2)∠BAD＝60°，AC平分∠BAD，AC＝2，求BN的长．
25．已知，如图，在 ABCD中，E是CD的中点，F是AE的中点，FC与BE交于点G.求证：GF＝GC.
26．已知：如图，E为□ABCD中DC边的延长线上的一点，且CE＝DC，连结AE分别交BC、BD于点F、G，连结AC交BD于O，连结OF．求证：AB＝2OF．
参考答案
1．B
【解析】△ABC中，D、E分别是AB、AC边上的中点，
∴DE是△ABC的中位线，
又∵BC=8，∴DE=4，
故选B.
2．C
【解析】∵三角形的三条中位线分别为3cm、4cm、6cm，
∴三角形的三边分别为6cm，8cm，12cm，
∴这个三角形的周长=6+8+12=26cm，
故选C．
3．A
【解析】∵在四边形ABCD中，M、N、P分别是AD、BC、BD的中点，
∴PN，PM分别是△CDB与△DAB的中位线，
∴PM=AB，PN=DC，
∵AB=CD，
∴PM=PN，
∴△PMN是等腰三角形，
∵∠MPN=130°，
∴∠PMN=（180°-∠MPN）÷2=25°，
故选A．
4．D
【解析】∵点E、F分别是△ABC中AC、AB边的中点，BE、CF相交于点G，
∴G为△ABC的重心，
∴2FG=GC，
∵FG=3，
∴GC=6，
∴CF=9．
故选D.
【点睛】本题主要考查了三角形重心的定义及性质，熟记三角形三边中线的交点叫做三角形的重心，重心到顶点的距离与重心到对边中点的距离之比为2：1是解题的关键.
5．D
【解析】试题分析：已知，在△ABC中，∠ACB=90°，AC=8，AB=10，根据勾股定理可得BC=6，又因DE垂直平分AC，∠ACB=90°，可得DE为△ABC的中位线，根据三角形的中位线定理可得DE=BC=3，故答案选D.
6．B
【解析】试题分析：在RT△ABC中，∵∠ABC=90°，AB=8，BC=6，∴AC===10，∵DE是△ABC的中位线，∴DF∥BM，DE=BC=3，∴∠EFC=∠FCM，∵∠FCE=∠FCM，∴∠EFC=∠ECF，∴EC=EF=AC=5，∴DF=DE+EF=3+5=8．故选B．
7．平行四边形
【解析】
试题分析：由三角形的中位线的性质，平行与第三边且等于第三边的一半，根据一组对边平行且相等的四边形是平行四边形.
8．14cm
【解析】∵E、F、G、H分别是边AB、BC、CD、DA的中点，AC=6cm，BD=8cm，
∴EH=FG=BD=4cm，EF=HG=AC=3cm，
∴四边形EFGH的周长为：（EH+FG）+（EF+HG）=4×2+3×2 =8+6=14cm，
故答案为14cm．
9．44
【解析】∵E、F是AC，CB的中点，
∴EF是△ABC的中位线，
∴EF=AB，
∵EF=22m，
∴AB=44m，
故答案为44．
【点睛】本题考查了三角形的中位线定理在实际生活中的运用，解题的关键是熟知三角形中位线定理的内容.
10．1∶4
【解析】如图，∵AD=DB，AE=EC，
∴DE∥BC．DE=BC，
∴△ADE∽△ABC，
∴，
故答案为．
11．11
【解析】试题解析：∵BD⊥DC，BD=4，CD=3，由勾股定理得 EMBED Equation.DSMT4 ，
∵E、F、G、H分别是AB、AC、CD、BD的中点，
∴HG=BC=EF，EH=FG=AD，
∵AD="6，"
∴EF="HG=2.5，EH=GF=3，"
∴四边形EFGH的周长是EF+FG+HG+EH=2×（2.5+3）=11．
12． 16 EMBED Equation.DSMT4
【解析】∵如图，△ABC的周长为64，E、F、G分别为AB、AC、BC的中点，
∴EF、FG、EG为三角形中位线，
∴EF=BC，EG=AC，FG=AB，
∴EF+FG+EG=（BC+AC+AB），即△EFG的周长是△ABC周长的一半，
同理，△A′B′C′的周长是△EFG的周长的一半，即△A′B′C′的周长为×64=16，
以此类推，第n个小三角形的周长是第一个三角形周长的64×（）n-1，
故答案为：16，64×（）n-1．
13．25
【解析】试题分析：依据AB=BC=3DE=12，即可求得DE、AB、BC的长，利用三角形的中位线定理即可求得GF和EF的长，根据直角三角形斜边上的中线等于斜边的一半，求得DG的长，则四边形的周长即可求解．
试题解析：∵AB=BC=3DE=12，∴BC=18，DE=4，
∵AD⊥BC，G是AB的中点，∴DG=AB=6，
∵E，F，G分别是BC，AC，AB的中点，
∴FG=BC=9，EF=AB=6，
∴四边形DEFG的周长为4+6+9+6=25.
【点睛】本题考查了三角形中位线定理，直角三角形斜边上的中线的性质等，解题的关键是结合图形灵活应用相关的定理与性质．
14．证明见解析.
【解析】试题分析：根据BD，CE是△ABC的中线可得DE是△ABC的中位线，F，G分别是OB，OC的中点可得FG是△BOC的中位线，根据三角形中位线定理可得DE∥BC且DE=BC，FG∥BC且FG=BC，进而可得DE∥FG且DE=FG，根据一组对边平行且相等的四边形是平行四边形可得结论.
试题解析：∵BD、CE是△ABC的中线，∴DE是△ABC的中位线，
∴DE∥BC且DE＝BC，
∵F、F分别是BO、CO的中点，∴FG是△BCG的中位线，
∴FG∥BC且FG＝BC，
∴DE∥FG且DE＝FG，
∴四边形DEFG是平行四边形.
15．证明过程见解析.
【解析】试题分析：直接证明DE= (AB+AC)比较困难，注意到E是BC的中点，联想到三角形的中位线定理，于是延长CD与BA交于F点，只需证D是CF的中点及AF=AC即可，这容易从题设证得.
试题解析：延长CD与BA交于F点.
∵AD是∠BAC的外角平分线，∴∠CAD=∠EAD，
∵CD⊥AD，∴∠ADC=∠ADF=90°，∴∠ACD=∠F，
∴AC=AF，∴CD=DF，
∵E是BC的中点，∴DE=BF= (AB+AC).
16．证明见解析.
【解析】试题分析：连接AC，取AC中点为M，连接ME、MF，根据中位线定理证明EM=MF，从而可得∠MEF=∠MFE，根据平行线同位角相等，证明∠MEF=∠AHF，∠MFE=∠BGF，可以求证∠AHF=∠BGF．
试题解析：连接AC，取AC中点为M，连接ME、MF，如图：
∵E是CD的中点，M为AC中点，
∴EM∥AD，且EM=AD，
∵M是AC的中点， F是AB的中点，
∴MF∥BC，且MF=BC，
∵AD=BC，
∴EM=MF，∴∠MEF=∠MFE，
∵EM∥AH，∴∠MEF=∠AHF，
∵FM∥BG，∴∠MFE=∠BGF，
∴∠AHF=∠BGF．
17．ED=1.
【解析】延长BE交AC于F，
∵AE平分∠BAC，
∴∠BAE＝∠CAE，
∵BE⊥AE，AE＝AE，
∴△ABE≌△AFE，
∴AF＝AB，BE＝EF，
∵AB＝5，
∴AF＝5，
∵AC＝7，
∴CF＝AC-AF＝7-5＝2，
∵D为BC中点，
∴BD＝CD，
∴DE是△BCF的中位线，
∴DE＝CF＝1.
【点睛】本题主要考查了全等三角形的判定与性质、三角形中位线定理，解题的关键是正确添加辅助线.
18．AP=AQ，理由见解析.
【解析】根据中位线定理证明MH=NH，进而证明∠HMN=∠HNM，∠HMN=∠PQA，所以△APQ为等腰三角形，即AP=AQ．
19．△DOE的周长为15.
【解析】试题分析：根据平行四边形的对边相等和对角线互相平分可得，OB=OD，又因为E点是CD的中点，可得OE是△BCD的中位线，可得OE= EMBED Equation.DSMT4 BC，所以易求△DOE的周长．
试题解析：∵平行四边形ABCD的周长为36，
∴2（BC+CD）=36，则BC+CD=18．
∵四边形ABCD是平行四边形，对角线AC，BD相交于点O，BD=12，
∴OD=OB=BD=6．
又∵点E是CD的中点，
∴OE是△BCD的中位线，DE=CD，
∴OE=BC，
∴△DOE的周长=OD+OE+DE=BD+（BC+CD）=6+9=15，
即△DOE的周长为15．
20．（1）证明见解析；（2）证明见解析.
【解析】试题分析：（1）根据角平分线的性质及平行线的性质易∠AEF=∠AFE，即可得AE=AF；（2）作CG∥EM，交BA的延长线于G，已知AC=AG，根据三角形中位线定理的推论证明BE=EG，再利用三角形的中位线定理即可证得结论．
试题解析：
（1）∵DA平分∠BAC，
∴∠BAD=∠CAD，
∵AD∥EM，
∴∠BAD=∠AEF，∠CAD=∠AFE，
∴∠AEF=∠AFE，
∴AE=AF．
（2）作CG∥EM，交BA的延长线于G．
∵EF∥CG，
∴∠G=∠AEF，∠ACG=∠AFE，
∵∠AEF=∠AFE，
∴∠G=∠ACG，
∴AG=AC，
∵BM=CM．EM∥CG，
∴BE=EG，
∴BE=BG=（BA+AG）=（AB+AC）．
21．（1）作图见解析;（2）BC=8．
【解析】试题分析：（1）作线段 EMBED Equation.DSMT4 的垂直平分线即可．
（2）根据三角形中位线定理即可解决．
试题解析：（1）作线段的垂直平分线交于,点就是所求的点．
（2）分别为的中点，
22．（1）证明见解析；（2）BG＝2GE.
【解析】试题分析：（1）根据BE，CF是△ABC的中线可得EF是△ABC的中位线，P，Q分别是BG，CG的中点可得PQ是△BCG的中位线，根据三角形中位线定理可得EF∥BC且EF=BC，PQ∥BC且PQ=BC，进而可得EF∥PQ且EF=PQ，根据一组对边平行且相等的四边形是平行四边形可得结论；
（2）根据平行四边形的性质可得GE=GP，再根据P是BG的中点可得BG=2PG，利用等量代换可得答案．
试题解析：（1）∵BE、CF是△ABC的中线，∴EF是△ABC的中位线，
∴EF∥BC且EF＝BC，
∵P、Q分别是BG、CG的中点，∴PQ是△BCG的中位线，
∴PQ∥BC且PQ＝BC，
∴EF∥PQ且EF＝PQ，
∴四边形EFPQ是平行四边形；
（2）BG＝2GE，
∵四边形EFPQ是平行四边形，∴GP＝GE，
∵P是BG中点，∴BG＝2PG，
∴BG＝2GE.
23．证明见解析.
【解析】试题分析：连接EM、EN、FM、FN，证明四边形EMFN为平行四边形，根据平行四边形对角线互相平分即可得.
试题解析：连接EM、EN、FM、FN，
∵E为AD的中点，N为AC的中点，
∴EN是△ACD的是位线，
∴EN∥CD，EN＝CD，
同理MF∥CD，MF＝CD，
∴EN∥MF，EN＝MF，
∴四边形EMFN为平行四边形，
∴EF与MN互相平分．
【点睛】本题考查了三角形的中位线定理，平行四边形的判定与性质，正确添加辅助线、熟记定理和性质是解题的关键．
24．（1）证明见解析；（2）BN＝ EMBED Equation.DSMT4 .
【解析】试题分析：（1）在△CAD中，由中位线定理得到MN∥AD，且MN=AD，在Rt△ABC中，因为M是AC的中点，故BM=AC，即可得到结论；
（2）由∠BAD=60°且AC平分∠BAD，得到∠BAC=∠DAC=30°，由（1）知，BM=AC=AM=MC，得到∠BMC =60°．由平行线性质得到∠NMC=∠DAC=30°，故∠BMN90°，得到，再由MN=BM=1，得到BN的长．
试题解析：（1）在△CAD中，∵M、N分别是AC、CD的中点，∴MN∥AD，且MN=AD，在Rt△ABC中，∵M是AC的中点，∴BM=AC，又∵AC=AD，∴MN=BM；
（2）∵∠BAD=60°且AC平分∠BAD，∴∠BAC=∠DAC=30°，由（1）知，BM=AC=AM=MC，∴∠BMC=∠BAM+∠ABM=2∠BAM=60°．∵MN∥AD，∴∠NMC=∠DAC=30°，∴∠BMN=∠BMC+∠NMC=90°，∴，而由（1）知，MN=BM=AC=×2=1，∴BN=．
25．证明见解析
【解析】试题分析：取BE的中点H，连接FH，CH，利用三角形中位线定理求FH＝AB,利用平行四边形判断定理可得到CEFH是平行四边形，所以GF＝GC.
试题解析：
取BE的中点H，连接FH，CH，∵F是AE的中点，∴FH∥AB，FH＝AB.∵CD∥AB，CD＝AB，CE＝CD，∴CE∥FH，且CE＝FH.∴四边形CEFH是平行四边形．∴GF＝GC.
26．证明见解析.
【解析】
试题分析：先证明△ABF≌△ECF得BF=FC，再利用三角形中位线定理即可解决问题．
试题解析：∵四边形ABCD是平行四边形，
∴AB=CD，AB∥CD，AO=OC，
∵CD=CE，
∴AB=CE，∠BAF=∠CEF，
在△ABF和△ECF中，
，
∴△ABF≌△ECF，
∴BF=FC，
∵AO=OC，
∴AB=2OF．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)