4.2.1平移与平移的性质 练习
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
4.2.1 平移与平移的性质
班级:___________姓名:___________得分:__________
(满分:100分,考试时间:40分钟)
一.选择题(共5小题,每题8分)
1.下列生活中的各个现象,属于平移变换现象的是( )
A.拉开抽屉 B.用放大镜看文字
C.时钟上分针的运动 D.你和平面镜中的像
2.将图中所示的图案平移后得到的图案是( )
A. B. C. D.
3.下列图形中,不能通过其中一个四边形平移得到的是( )
A. B. C. D.
4.如图,在10×6的网格中,每个小正方形的边长都是1个单位,将三角形ABC平移到三角形DEF的位置,下面正确的平移步骤是( )21·cn·jy·com
A.先向左平移5个单位,再向下平移2个单位
B.先向右平移5个单位,再向下平移2个单位
C.先向左平移5个单位,再向上平移2个单位
D.先向右平移5个单位,再向上平移2个单位
5.如图图形中,把△ABC平移后能得到△DEF的是( )
A. B.
C. D.
二.填空题(共4小题,每题5分)
6.用4根木棍可拼成大写的英文字母“M”,平移其中一根木棍,你能得到另一个大写的英文字母,请写出这个英文字母 .www.21-cn-jy.com
7.如图是一块从一个边长为50cm的正方形材料中剪出的垫片,现测得FG=5cm,则这个剪出的图形的周长是 cm.21·世纪*教育网
8.如图,∠1=70°,直线a平移后得到直线b,则∠2﹣∠3= °.
9.如下图所示,图中为一块矩形ABCD的场地,AB=102m,AD=51m,从A,B两地入口的路宽都为1m,两小路汇合处的路宽为2m,其余部分种植草坪,那么草坪的面积为 m2.21*cnjy*com
三.解答题(共3小题,第10、12题各15分,第11题10分)
10.若在方格(每小格正方形边长为1m)上沿着网格线平移,规定:沿水平方向平移的数量为a(向右为正,向左为负,平移|a|个单位),沿竖直方向平移的数量为b(向上为正,向下为负,平移|b|个单位),则把有序数对{a,b}叫做这一平移的“平移量”.例如:点A按“平移量”{1,4}可平移至点B.【来源:21cnj*y.co*m】
(1)从点C按“平移量”{ , }可平移到点B;
(2)若点B依次按“平移量”{4,﹣3}、{﹣2,1}平移至点D,
①请在图中标出点D;(用黑色水笔在答题卡上作出点D)
②如果每平移1m需要2.5秒,那么按此方法从点B移动至点D需要多少秒?
③观察点D的位置,其实点B也可按“平移量”{ , }直接平移至点D;观察这两种平移的“平移量”,猜想:点E依次按“平移量”{2a,3b}、{﹣5a,b}、{a,﹣5b}平移至点F,则相当于点E按“平移量”{ , }直接平移至点F.
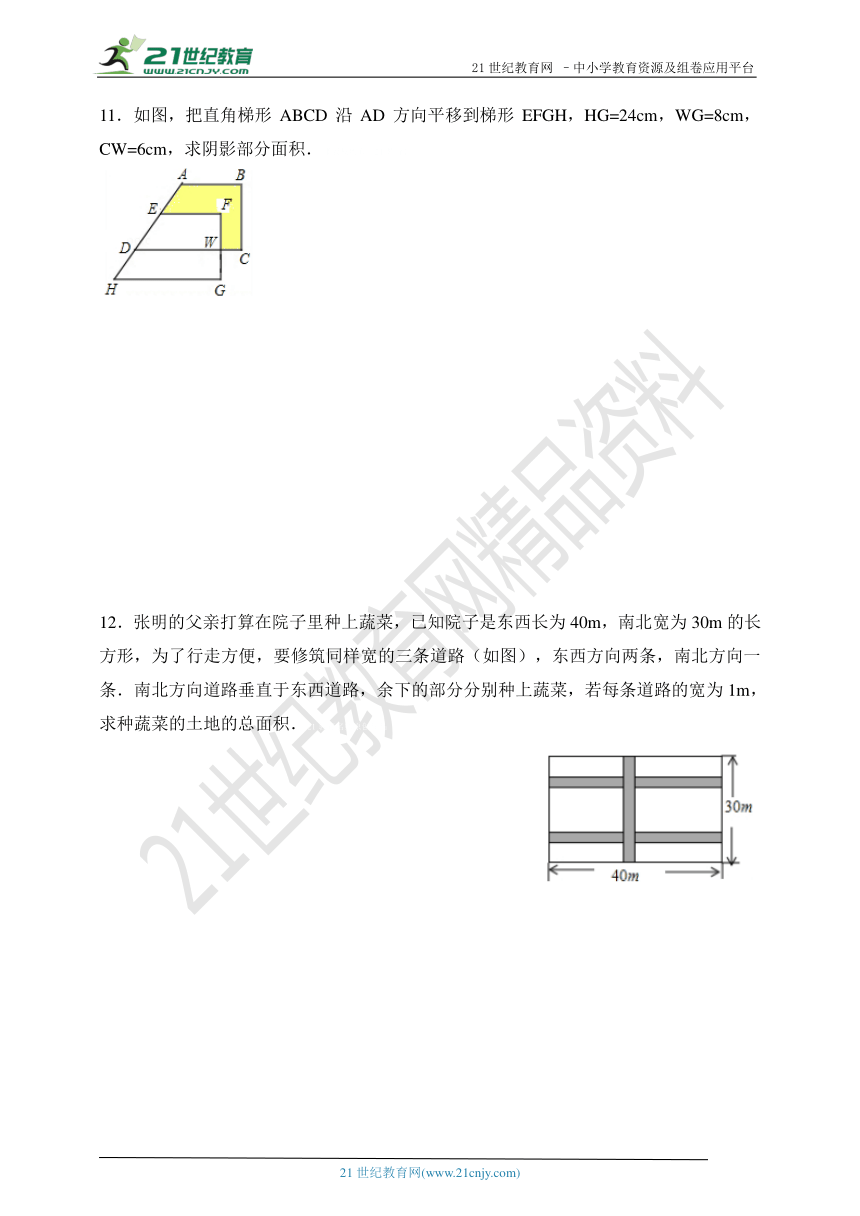
11.如图,把直角梯形ABCD沿AD方向平移到梯形EFGH,HG=24cm,WG=8cm,CW=6cm,求阴影部分面积.【版权所有:21教育】
12.张明的父亲打算在院子里种上蔬菜,已知院子是东西长为40m,南北宽为30m的长方形,为了行走方便,要修筑同样宽的三条道路(如图),东西方向两条,南北方向一条.南北方向道路垂直于东西道路,余下的部分分别种上蔬菜,若每条道路的宽为1m,求种蔬菜的土地的总面积.21教育名师原创作品
试题解析
一.选择题
1.A
【分析】根据平移的定义直接判断即可.
【解答】解:A、是平移;B、大小发生变化,不是平移;C、是旋转;D、你和平面镜中的像不是平移,是轴对称.故选:A.21cnjy.com
【点评】本题考查了图形的平移,图形的平移只改变图形的位置,而不改变图形的形状和大小,学生易混淆图形的平移与旋转或翻转而误选.21*cnjy*com
2.C
【分析】根据平移的性质,不改变图形的形状和大小,经过平移,对应点所连的线段平行且相等,对应线段平行且相等.
【解答】解:通过图案平移得到必须与图案完全相同,角度也必须相同,
观察图形可知C可以通过图案平移得到.
故选:C.
【点评】本题考查平移的基本性质是:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.
3.D
【分析】根据平移与旋转的性质得出.
【解答】解:A、能通过其中一个四边形平移得到,错误;
B、能通过其中一个四边形平移得到,错误;
C、能通过其中一个四边形平移得到,错误;
D、不能通过其中一个四边形平移得到,需要一个四边形旋转得到,正确.
故选:D.
【点评】本题考查了图形的平移,图形的平移只改变图形的位置,而不改变图形的形状和大小,学生易混淆图形的平移与旋转或翻转,导致误选.21教育网
4.A
【分析】根据网格结构,可以利用一对对应点的平移关系解答.
【解答】解:根据网格结构,观察对应点A、D,点A向左平移5个单位,再向下平移2个单位即可到达点D的位置,【来源:21·世纪·教育·网】
所以平移步骤是:先把△ABC向左平移5个单位,再向下平移2个单位.
故选:A.
【点评】本题考查了坐标与图形变化﹣平移,利用对应点的平移规律确定图形的平移规律是解题的关键.
5.A
【分析】根据图形平移的性质对各选项进行逐一分析即可.
【解答】解:A、△DEF由△ABC平移而成,故本选项正确;
B、△DEF由△ABC对称而成,故本选项错误;
C、△DEF由△ABC旋转而成,故本选项错误;
D、△DEF由△ABC对称而成,故本选项错误.
故选:A.
【点评】本题考查的是平移的性质,熟知把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同是解答此题的关键.
二.填空题
6. W .
【分析】根据平移的性质,将最左边的木棍移到右边即可得到字母W.
【解答】解:如图,
能得到大写英文字母W.
故答案为:W.
【点评】本题考查了平移的性质,比较简单,主要是英文字母M、W之间的关系.
7. 210 cm.
【分析】利用平移的性质将EF,GH,AH,分别向左和上平移即可得出平移后图形,进而求出这块垫片的周长.【出处:21教育名师】
【解答】解:如图所示:这块垫片的周长为:50×4+FG+NH=200+10=210(cm),
故答案为:210.
【点评】本题考查了生活中的平移现象,利用平移的性质得出是解题关键.
8. 110 °.
【分析】延长直线后根据平行线的性质和三角形的外角性质解答即可.
【解答】解:延长直线,如图:,
∵直线a平移后得到直线b,
∴a∥b,
∴∠5=180°﹣∠1=180°﹣70°=110°,
∵∠2=∠4+∠5,
∵∠3=∠4,
∴∠2﹣∠3=∠5=110°,
故答案为:110.
【点评】此题考查平移问题,关键是根据平行线的性质和三角形的外角性质解答.
9. 5000 m2.
【分析】本题主要利用矩形的性质求出长和宽,再进行解答.
【解答】解:由图可知:矩形ABCD中去掉小路后,草坪正好可以拼成一个新的矩形,且它的长为:102﹣2=100,宽为51﹣1=50.所以草坪的面积应该是长×宽=100×50=5000.
故选:5000.
【点评】本题考查矩形的性质及空间想象能力,有一定的思维容量.
三.解答题
10.【分析】(1)根据图形,点B在点C的左边2个单位,下方1个单位,再根据“平移量”的定义即可求解;2·1·c·n·j·y
(2)①根据“平移量”的定义确定出点D的位置即可;
②根据“平移量”的定义求出从点B移动到点D的路程,然后乘以2.5,计算即可得解;
③根据“平移量”的定义结合直接写出点B到点D的平移量即可;把从点E到点F所有平移量的横向相加,纵向相加,计算即可得解.www-2-1-cnjy-com
【解答】解:(1)从C到B,向左2个单位,向下1个单位,
所以,平移量为{﹣2,﹣1};
(2)①点B依次按“平移量”{4,﹣3}、{﹣2,1}平移至点D如图所示;
②(4+3+2+1)×2.5=10×2.5=25秒;
③由图可知,点B到点D,向右2个单位,向下2个单位,
所以,平移量为{2,﹣2},
∵2a﹣5a+a=﹣2a,
3b+b﹣5b=﹣b,
∴点E到F的平移量为{﹣2a,﹣b}.
故答案为:(1)﹣2,﹣1;(2)③2,﹣2;﹣2a,﹣b.
【点评】本题考查了平移的性质,平移量的定义,读懂题目信息,理解平移量的定义并熟练掌握网格结构是解题的关键.2-1-c-n-j-y
11.【分析】根据平移的变换只改变图形的位置不改变图形的形状与大小可得梯形ABCD的面积等于梯形EFGH的面积,CD=HG,从而得到阴影部分的面积等于梯形DWGH的面积,再求出DW的长,然后利用梯形的面积公式列式计算即可得解.
【解答】解:由平移的性质,梯形ABCD的面积=梯形EFGH的面积,CD=HG=24cm,
∴阴影部分的面积=梯形DWGH的面积,
∵CW=6cm,
∴DW=CD﹣CW=24﹣6=18cm,
∴阴影部分的面积=(DW+HG) WG=(18+24)×8=168cm2.
答:阴影部分面积是168cm2.
【点评】本题考查了平移的性质,根据图形判断出阴影部分的面积等于梯形DWGH的面积是解题的关键,也是本题的难点.21世纪教育网版权所有
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
4.2.1 平移与平移的性质
班级:___________姓名:___________得分:__________
(满分:100分,考试时间:40分钟)
一.选择题(共5小题,每题8分)
1.下列生活中的各个现象,属于平移变换现象的是( )
A.拉开抽屉 B.用放大镜看文字
C.时钟上分针的运动 D.你和平面镜中的像
2.将图中所示的图案平移后得到的图案是( )
A. B. C. D.
3.下列图形中,不能通过其中一个四边形平移得到的是( )
A. B. C. D.
4.如图,在10×6的网格中,每个小正方形的边长都是1个单位,将三角形ABC平移到三角形DEF的位置,下面正确的平移步骤是( )21·cn·jy·com
A.先向左平移5个单位,再向下平移2个单位
B.先向右平移5个单位,再向下平移2个单位
C.先向左平移5个单位,再向上平移2个单位
D.先向右平移5个单位,再向上平移2个单位
5.如图图形中,把△ABC平移后能得到△DEF的是( )
A. B.
C. D.
二.填空题(共4小题,每题5分)
6.用4根木棍可拼成大写的英文字母“M”,平移其中一根木棍,你能得到另一个大写的英文字母,请写出这个英文字母 .www.21-cn-jy.com
7.如图是一块从一个边长为50cm的正方形材料中剪出的垫片,现测得FG=5cm,则这个剪出的图形的周长是 cm.21·世纪*教育网
8.如图,∠1=70°,直线a平移后得到直线b,则∠2﹣∠3= °.
9.如下图所示,图中为一块矩形ABCD的场地,AB=102m,AD=51m,从A,B两地入口的路宽都为1m,两小路汇合处的路宽为2m,其余部分种植草坪,那么草坪的面积为 m2.21*cnjy*com
三.解答题(共3小题,第10、12题各15分,第11题10分)
10.若在方格(每小格正方形边长为1m)上沿着网格线平移,规定:沿水平方向平移的数量为a(向右为正,向左为负,平移|a|个单位),沿竖直方向平移的数量为b(向上为正,向下为负,平移|b|个单位),则把有序数对{a,b}叫做这一平移的“平移量”.例如:点A按“平移量”{1,4}可平移至点B.【来源:21cnj*y.co*m】
(1)从点C按“平移量”{ , }可平移到点B;
(2)若点B依次按“平移量”{4,﹣3}、{﹣2,1}平移至点D,
①请在图中标出点D;(用黑色水笔在答题卡上作出点D)
②如果每平移1m需要2.5秒,那么按此方法从点B移动至点D需要多少秒?
③观察点D的位置,其实点B也可按“平移量”{ , }直接平移至点D;观察这两种平移的“平移量”,猜想:点E依次按“平移量”{2a,3b}、{﹣5a,b}、{a,﹣5b}平移至点F,则相当于点E按“平移量”{ , }直接平移至点F.
11.如图,把直角梯形ABCD沿AD方向平移到梯形EFGH,HG=24cm,WG=8cm,CW=6cm,求阴影部分面积.【版权所有:21教育】
12.张明的父亲打算在院子里种上蔬菜,已知院子是东西长为40m,南北宽为30m的长方形,为了行走方便,要修筑同样宽的三条道路(如图),东西方向两条,南北方向一条.南北方向道路垂直于东西道路,余下的部分分别种上蔬菜,若每条道路的宽为1m,求种蔬菜的土地的总面积.21教育名师原创作品
试题解析
一.选择题
1.A
【分析】根据平移的定义直接判断即可.
【解答】解:A、是平移;B、大小发生变化,不是平移;C、是旋转;D、你和平面镜中的像不是平移,是轴对称.故选:A.21cnjy.com
【点评】本题考查了图形的平移,图形的平移只改变图形的位置,而不改变图形的形状和大小,学生易混淆图形的平移与旋转或翻转而误选.21*cnjy*com
2.C
【分析】根据平移的性质,不改变图形的形状和大小,经过平移,对应点所连的线段平行且相等,对应线段平行且相等.
【解答】解:通过图案平移得到必须与图案完全相同,角度也必须相同,
观察图形可知C可以通过图案平移得到.
故选:C.
【点评】本题考查平移的基本性质是:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.
3.D
【分析】根据平移与旋转的性质得出.
【解答】解:A、能通过其中一个四边形平移得到,错误;
B、能通过其中一个四边形平移得到,错误;
C、能通过其中一个四边形平移得到,错误;
D、不能通过其中一个四边形平移得到,需要一个四边形旋转得到,正确.
故选:D.
【点评】本题考查了图形的平移,图形的平移只改变图形的位置,而不改变图形的形状和大小,学生易混淆图形的平移与旋转或翻转,导致误选.21教育网
4.A
【分析】根据网格结构,可以利用一对对应点的平移关系解答.
【解答】解:根据网格结构,观察对应点A、D,点A向左平移5个单位,再向下平移2个单位即可到达点D的位置,【来源:21·世纪·教育·网】
所以平移步骤是:先把△ABC向左平移5个单位,再向下平移2个单位.
故选:A.
【点评】本题考查了坐标与图形变化﹣平移,利用对应点的平移规律确定图形的平移规律是解题的关键.
5.A
【分析】根据图形平移的性质对各选项进行逐一分析即可.
【解答】解:A、△DEF由△ABC平移而成,故本选项正确;
B、△DEF由△ABC对称而成,故本选项错误;
C、△DEF由△ABC旋转而成,故本选项错误;
D、△DEF由△ABC对称而成,故本选项错误.
故选:A.
【点评】本题考查的是平移的性质,熟知把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同是解答此题的关键.
二.填空题
6. W .
【分析】根据平移的性质,将最左边的木棍移到右边即可得到字母W.
【解答】解:如图,
能得到大写英文字母W.
故答案为:W.
【点评】本题考查了平移的性质,比较简单,主要是英文字母M、W之间的关系.
7. 210 cm.
【分析】利用平移的性质将EF,GH,AH,分别向左和上平移即可得出平移后图形,进而求出这块垫片的周长.【出处:21教育名师】
【解答】解:如图所示:这块垫片的周长为:50×4+FG+NH=200+10=210(cm),
故答案为:210.
【点评】本题考查了生活中的平移现象,利用平移的性质得出是解题关键.
8. 110 °.
【分析】延长直线后根据平行线的性质和三角形的外角性质解答即可.
【解答】解:延长直线,如图:,
∵直线a平移后得到直线b,
∴a∥b,
∴∠5=180°﹣∠1=180°﹣70°=110°,
∵∠2=∠4+∠5,
∵∠3=∠4,
∴∠2﹣∠3=∠5=110°,
故答案为:110.
【点评】此题考查平移问题,关键是根据平行线的性质和三角形的外角性质解答.
9. 5000 m2.
【分析】本题主要利用矩形的性质求出长和宽,再进行解答.
【解答】解:由图可知:矩形ABCD中去掉小路后,草坪正好可以拼成一个新的矩形,且它的长为:102﹣2=100,宽为51﹣1=50.所以草坪的面积应该是长×宽=100×50=5000.
故选:5000.
【点评】本题考查矩形的性质及空间想象能力,有一定的思维容量.
三.解答题
10.【分析】(1)根据图形,点B在点C的左边2个单位,下方1个单位,再根据“平移量”的定义即可求解;2·1·c·n·j·y
(2)①根据“平移量”的定义确定出点D的位置即可;
②根据“平移量”的定义求出从点B移动到点D的路程,然后乘以2.5,计算即可得解;
③根据“平移量”的定义结合直接写出点B到点D的平移量即可;把从点E到点F所有平移量的横向相加,纵向相加,计算即可得解.www-2-1-cnjy-com
【解答】解:(1)从C到B,向左2个单位,向下1个单位,
所以,平移量为{﹣2,﹣1};
(2)①点B依次按“平移量”{4,﹣3}、{﹣2,1}平移至点D如图所示;
②(4+3+2+1)×2.5=10×2.5=25秒;
③由图可知,点B到点D,向右2个单位,向下2个单位,
所以,平移量为{2,﹣2},
∵2a﹣5a+a=﹣2a,
3b+b﹣5b=﹣b,
∴点E到F的平移量为{﹣2a,﹣b}.
故答案为:(1)﹣2,﹣1;(2)③2,﹣2;﹣2a,﹣b.
【点评】本题考查了平移的性质,平移量的定义,读懂题目信息,理解平移量的定义并熟练掌握网格结构是解题的关键.2-1-c-n-j-y
11.【分析】根据平移的变换只改变图形的位置不改变图形的形状与大小可得梯形ABCD的面积等于梯形EFGH的面积,CD=HG,从而得到阴影部分的面积等于梯形DWGH的面积,再求出DW的长,然后利用梯形的面积公式列式计算即可得解.
【解答】解:由平移的性质,梯形ABCD的面积=梯形EFGH的面积,CD=HG=24cm,
∴阴影部分的面积=梯形DWGH的面积,
∵CW=6cm,
∴DW=CD﹣CW=24﹣6=18cm,
∴阴影部分的面积=(DW+HG) WG=(18+24)×8=168cm2.
答:阴影部分面积是168cm2.
【点评】本题考查了平移的性质,根据图形判断出阴影部分的面积等于梯形DWGH的面积是解题的关键,也是本题的难点.21世纪教育网版权所有
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
