4.3.2 探索三角形全等的条件(第二课时)课件(共40张PPT)
文档属性
| 名称 | 4.3.2 探索三角形全等的条件(第二课时)课件(共40张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-08 00:00:00 | ||
图片预览




文档简介
课件40张PPT。4.3 探索三角形全等的条件2 利用“角边角”“角角边”
判定三角形全等第四章三角形勇于质疑,敢于展示你争我辩,快乐无限学习目标1.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程;
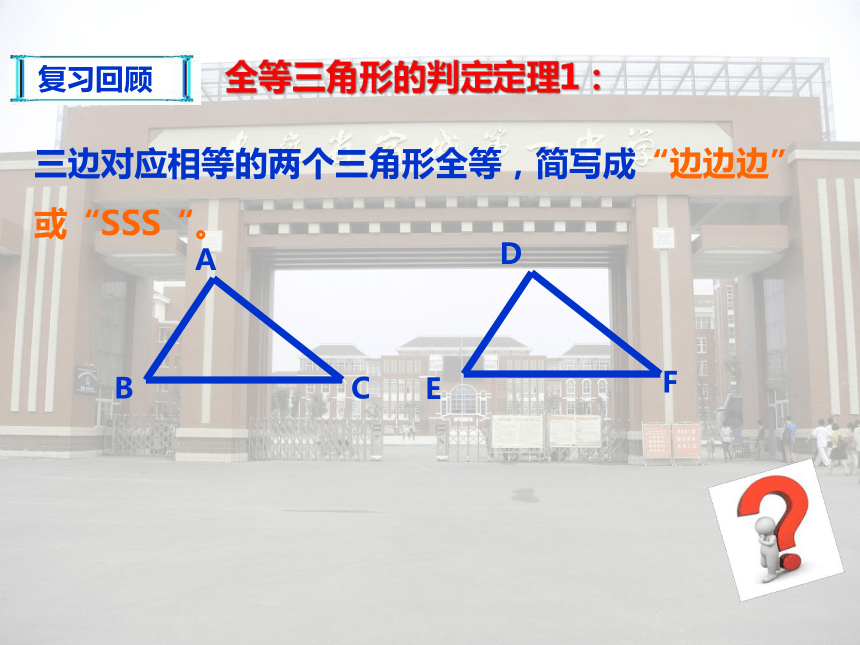
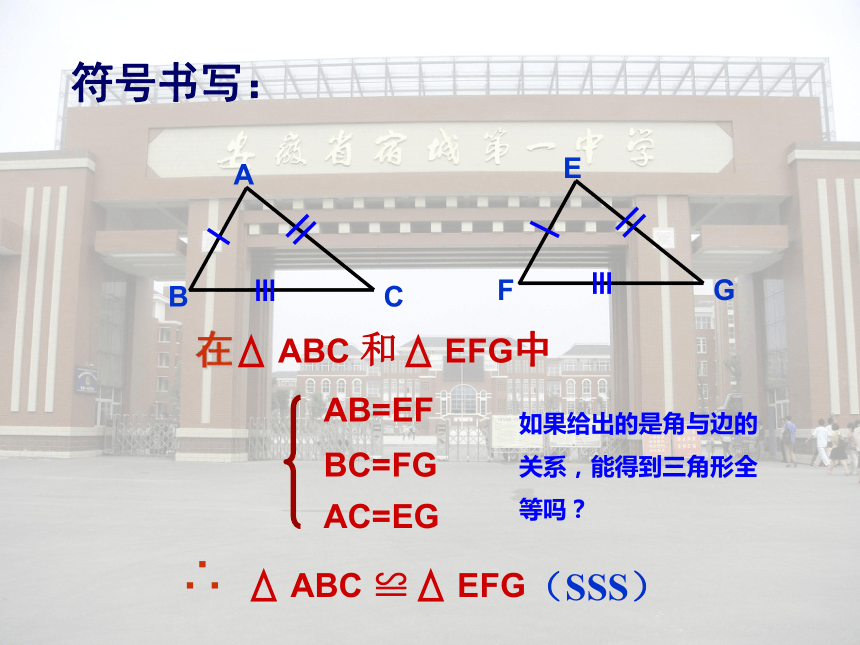
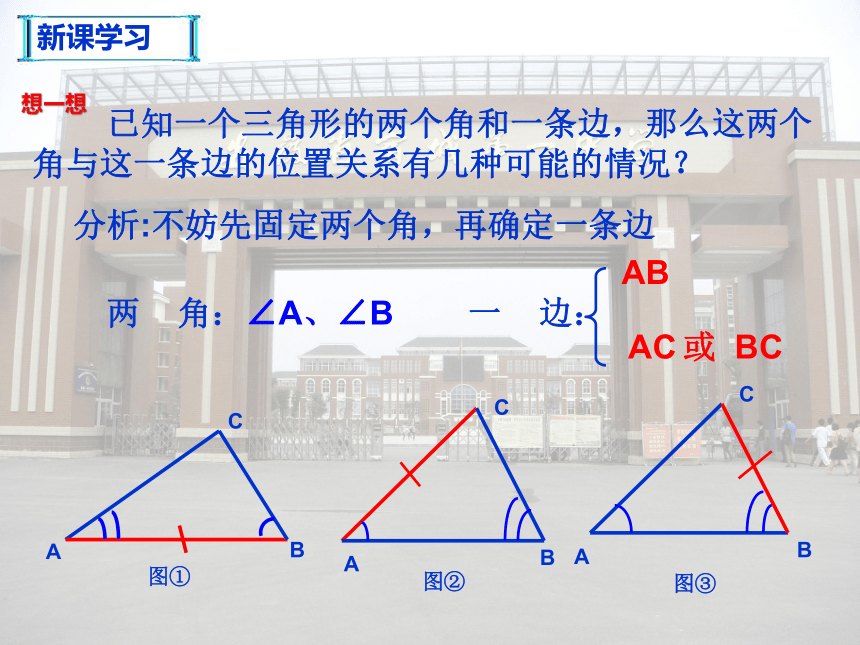
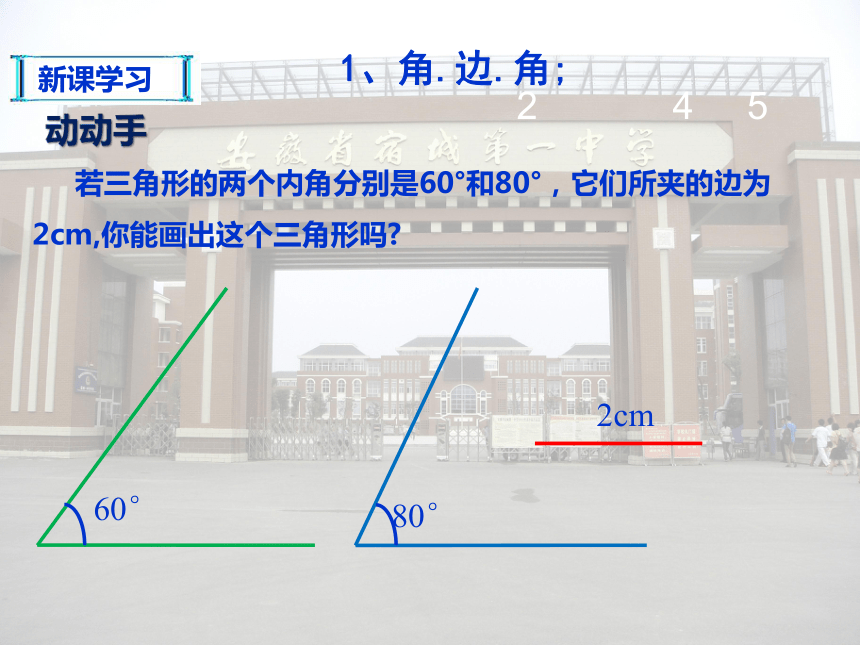
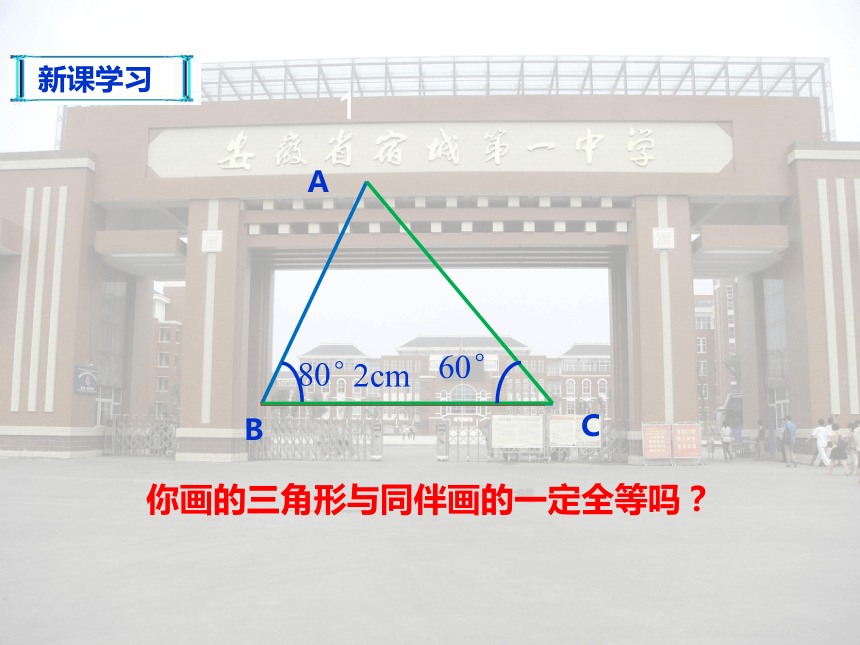
2. 掌握三角形全等的“ASA”和“AAS”条件;复习回顾ABCDEF三边对应相等的两个三角形全等,简写成“边边边”或“SSS“。全等三角形的判定定理1:AB=EFBC=FGAC=EG(SSS)符号书写:ABC 和 EFG中在∴如果给出的是角与边的关系,能得到三角形全等吗?情境引入 小明踢球时不慎把一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块于原来一样的三角形玻璃呢?如果可以,带哪块去合适呢?为什么? 已知一个三角形的两个角和一条边,那么这两个角与这一条边的位置关系有几种可能的情况?分析:不妨先固定两个角,再确定一条边ABAC或 BC新课学习想一想新课学习245 若三角形的两个内角分别是60°和80°,它们所夹的边为2cm,你能画出这个三角形吗?动动手1、角.边.角;新课学习1你画的三角形与同伴画的一定全等吗?ABC新课学习两角和它们的夹边对应相等的两个三角形全等.
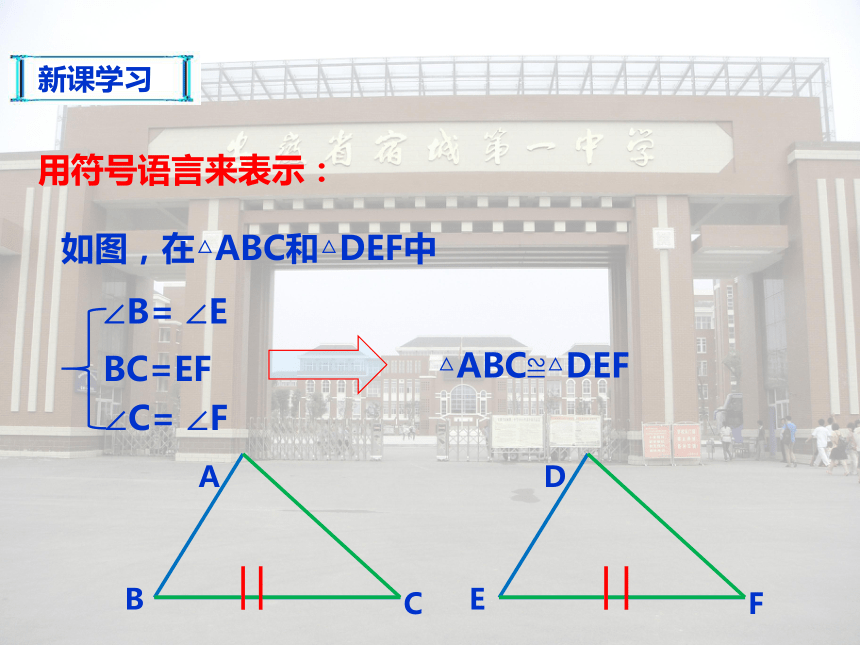
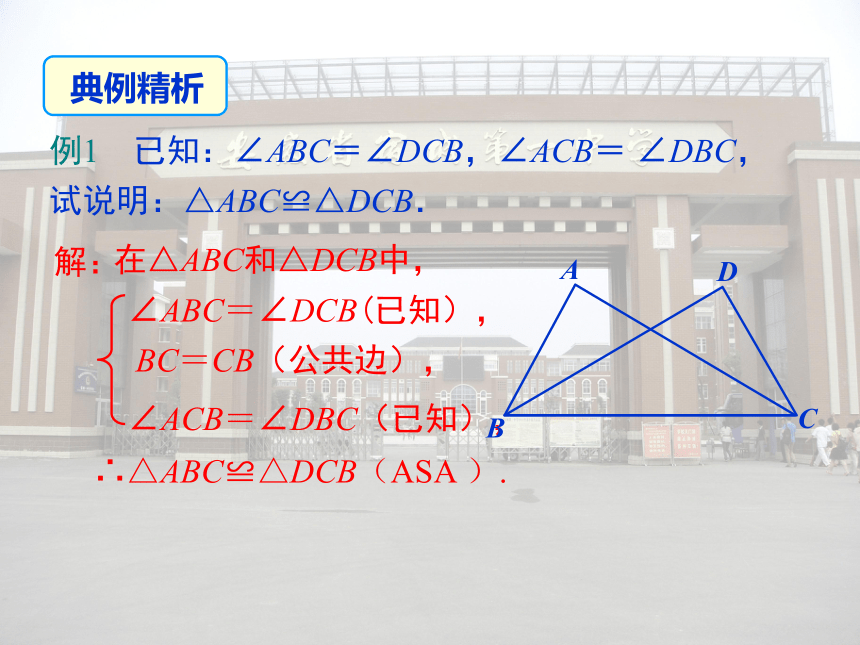
简写成“角边角”或“ASA”。全等三角形的判定定理2:要注意这里的边是两角的夹边哦!新课学习如图,在△ABC和△DEF中用符号语言来表示:∠B= ∠EBC=EF∠C= ∠F△ABC≌△DEFDEF例1 已知:∠ABC=∠DCB,∠ACB= ∠DBC,
试说明:△ABC≌△DCB.∠ABC=∠DCB(已知),
BC=CB(公共边),
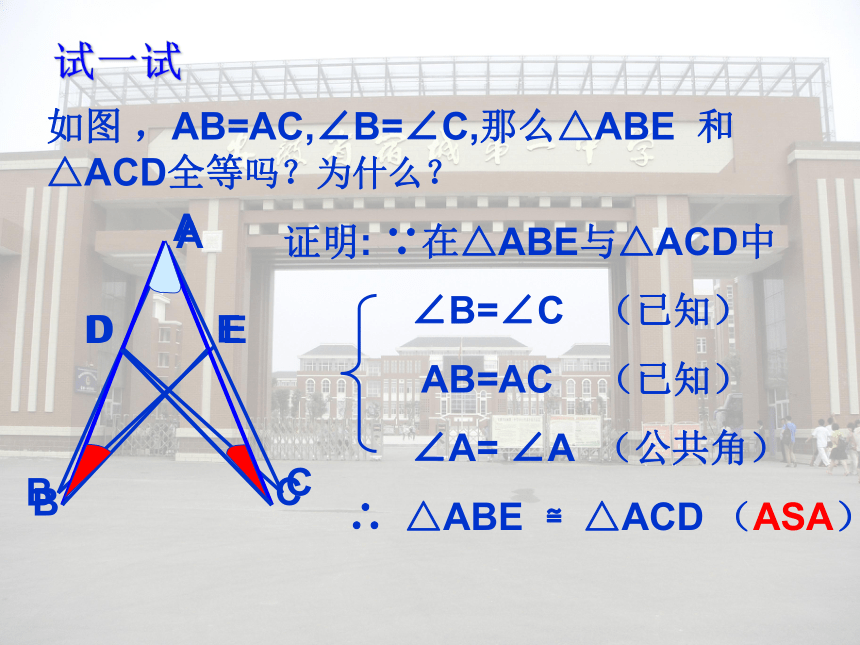
∠ACB=∠DBC(已知),解:在△ABC和△DCB中,∴△ABC≌△DCB(ASA ).ASA如图 ,AB=AC,∠B=∠C,那么△ABE 和△ACD全等吗?为什么?试一试新课学习 若三角形的两个内角分别是60°和45°,且45°所对的边为3cm,你能画出这个三角形吗?动动手新课学习你画的三角形与同伴画的一定全等吗?新课学习两角和其中一角的对边对应相等的两个三角形全等.简写成“角角边”或“AAS”.全等三角形的判定定理3:要注意这里的边是其中一角的对边,要注意区分!新课学习如图,在△ABC和△DEF中∠B= ∠EAC=DF∠C= ∠F△ABC≌△DEFDEF用符号语言来表示: 两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”。 两角和其中一角的对边对应相等的两个三角形全等,简写成“角角边”或“AAS”(ASA)例2 如图,AD∥BC,BE∥DF,AD=CB,
试说明:△ADF≌△CBE.解:∵AD∥BC,BE∥DF,
∴∠A=∠C,
∠DFE=∠BEC.在△ADF和△CBE中,∠A=∠C,
∠DFE=∠BEC,
AD=BC,∴△ADF≌△CBE(AAS).如图,AD=AE,∠B=∠C,那么BE和CD相等么?为什么?试一试1.如图,已知AB=DE, ∠A =∠D,∠B=∠E,则
△ABC≌△DEF的理由是 .2.如图,已知AB=DE ,∠A=∠D,∠C=∠F,则
△ABC≌△DEF的理由是________________角边角(ASA)角角边(AAS)练习巩固3: 如图,O是AB的中点,∠A= ∠B, △AOC与△BOD全等吗?为什么?小明两角和夹边对应相等(已知)(中点的定义)(对顶角相等)解:在 中4: 如图,O是AB的中点,∠C= ∠D, △AOC与△BOD全等吗?为什么?小明两角和一角的对边对应相等(已知)(中点的定义)(对顶角相等)解:在 中∠C= ∠D(AAS)5.已知 和 中, = ,AB=AC.求证: (1) (3) BD=CE证明: (2) AE=AD (全等三角形对应边相等)(已知)(已知)(公共角)(已知)(等式的性质) 6. 如图,已知∠ACB=∠DBC,∠ABC=∠CDB,判别
下面的两个三角形是否全等,并说明理由. 不全等,因为BC虽然是公共边,但不是对应边.提高练习1.如图,HI∥BJ,JI∥BH,求证:△BIH≌△IBJ。证明:∵HI∥BJ,JI∥BH,∴∠HIB=∠JBI,∠HBI=∠JIB,在△BIH和△IBJ中,∠HIB=∠JBI BI=IB ∠HBI=∠JIB ∴△BIH≌△IBJ(ASA)在 和 中2. 如图,AD = AE, ∠B = ∠C ,那么BE与CD相等吗?为什么?两角和其中一角的对应边对应相等(已知)(公共角)(已知)△ABE△ACD∠B = ∠C ∠A = ∠A AE= AD∴ △ABE≌△ACD(AAS)∴ BE=CD(全等三角形对应边相等)提高练习ABCDE123﹑如图,已知,∠C=∠E,∠1=∠2,AB=AD,△ABC和△ADE全等吗?为什么?解: △ABC和△ADE全等。
∵∠1=∠2(已知)
∴∠1+∠DAC=∠2+∠DAC
即∠BAC=∠DAE
在△ABC和△ADC 中 ∴ △ABC≌△ADE(AAS)我的感悟与收获课堂小结 两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”. 两角和其中一角的对边对应相等的两个三角形全等,简写成“角角边”或“AAS”.知识巩固1.如图,已知:∠A=∠D,要使△ABC≌△DCB,只需增加一个条件是( )
A.AC=DB B.BC=CB
C.∠ABC=∠DCB D.AB=DC C根据已知结合图形及判定方法选择条件知识巩固2.求证:在两个锐角三角形中,如果有两角及其中一角的对边上的高对应相等,那么这两个三角形全等。如图所示:已知:在△ABC和△DEF中,∠BAC=∠EDF,∠B=∠E,AM、DN分别是△ABC和△DEF的高,且AM=DN;
求证:△ABC≌△DEF。在△ABM和△DEN中,
∠B=∠E
∠AMB=∠DNE
AM=DN 知识巩固证明:∵AM、DN分别是△ABC和△DEF的高,
∴∠AMB=∠DNE=90°,∴△ABM≌△DEN(AAS),
∴AB=DE,在△ABC和△DEF中,
∠BAC=∠EDF
AB=DE
∠B=∠E
∴△ABC≌△DEF(ASA).知识巩固3.如图,AD∥BC,∠A=∠DEC=90°,DE=EC,试说明AD+BC=AB。再创辉煌:1、如图∠ACB=∠DFE,BC=EF,根据ASA或AAS,那么应补充一个直接条件 --------------------------,(写出一个即可),才能使△ABC≌△DEF2、如图,BE=CD,∠1=∠2,则AB=AC吗?为什么?ABCDEF∠B=∠E或∠A=∠D如图,AB∥CD,AD∥BC,那么AB=CD吗?为什么?AD与BC呢?五、思考题知识巩固证明:∵∠DEC=∠A=90°,
∴∠ADE+∠AED=90°,∠AED+∠BEC=90°,∴∠ADE=∠BEC,
∵AD∥BC,∠A=90°,∴∠B+∠A=180°,∴∠B=∠A=90°,
在△AED和△CEB中,
∠A=∠B
∠ADE=∠BEC
DE=EC ,
∴△AED≌△CEB,∴AE=BC,BE=AD,
∵AE+BE=AB,∴AD+BC=AB..如图,小明不慎将一块三角形模具打碎为三块,他是
否可以只带其中的一块碎片到商店去,就能配一块与
原来一样的三角形模具吗? 如果可以,带哪块去合
适?你能说明其中理由吗?答:带1去,因为有两角且夹边相等的两个三角形全等.知识的升华作业布置:
习题4.7老师期望:
做完题目后,一定要“悟”到点东西,纳入到自己的认知结构中去. 寄语: 亲:
只有不断的思考,才会有新的发现;只有量的变化,才会有质的进步.祝大家学有所得!
判定三角形全等第四章三角形勇于质疑,敢于展示你争我辩,快乐无限学习目标1.经历探索三角形全等条件的过程,体会利用操作、归纳获得数学结论的过程;
2. 掌握三角形全等的“ASA”和“AAS”条件;复习回顾ABCDEF三边对应相等的两个三角形全等,简写成“边边边”或“SSS“。全等三角形的判定定理1:AB=EFBC=FGAC=EG(SSS)符号书写:ABC 和 EFG中在∴如果给出的是角与边的关系,能得到三角形全等吗?情境引入 小明踢球时不慎把一块三角形玻璃打碎为两块,他是否可以只带其中的一块碎片到商店去,就能配一块于原来一样的三角形玻璃呢?如果可以,带哪块去合适呢?为什么? 已知一个三角形的两个角和一条边,那么这两个角与这一条边的位置关系有几种可能的情况?分析:不妨先固定两个角,再确定一条边ABAC或 BC新课学习想一想新课学习245 若三角形的两个内角分别是60°和80°,它们所夹的边为2cm,你能画出这个三角形吗?动动手1、角.边.角;新课学习1你画的三角形与同伴画的一定全等吗?ABC新课学习两角和它们的夹边对应相等的两个三角形全等.
简写成“角边角”或“ASA”。全等三角形的判定定理2:要注意这里的边是两角的夹边哦!新课学习如图,在△ABC和△DEF中用符号语言来表示:∠B= ∠EBC=EF∠C= ∠F△ABC≌△DEFDEF例1 已知:∠ABC=∠DCB,∠ACB= ∠DBC,
试说明:△ABC≌△DCB.∠ABC=∠DCB(已知),
BC=CB(公共边),
∠ACB=∠DBC(已知),解:在△ABC和△DCB中,∴△ABC≌△DCB(ASA ).ASA如图 ,AB=AC,∠B=∠C,那么△ABE 和△ACD全等吗?为什么?试一试新课学习 若三角形的两个内角分别是60°和45°,且45°所对的边为3cm,你能画出这个三角形吗?动动手新课学习你画的三角形与同伴画的一定全等吗?新课学习两角和其中一角的对边对应相等的两个三角形全等.简写成“角角边”或“AAS”.全等三角形的判定定理3:要注意这里的边是其中一角的对边,要注意区分!新课学习如图,在△ABC和△DEF中∠B= ∠EAC=DF∠C= ∠F△ABC≌△DEFDEF用符号语言来表示: 两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”。 两角和其中一角的对边对应相等的两个三角形全等,简写成“角角边”或“AAS”(ASA)例2 如图,AD∥BC,BE∥DF,AD=CB,
试说明:△ADF≌△CBE.解:∵AD∥BC,BE∥DF,
∴∠A=∠C,
∠DFE=∠BEC.在△ADF和△CBE中,∠A=∠C,
∠DFE=∠BEC,
AD=BC,∴△ADF≌△CBE(AAS).如图,AD=AE,∠B=∠C,那么BE和CD相等么?为什么?试一试1.如图,已知AB=DE, ∠A =∠D,∠B=∠E,则
△ABC≌△DEF的理由是 .2.如图,已知AB=DE ,∠A=∠D,∠C=∠F,则
△ABC≌△DEF的理由是________________角边角(ASA)角角边(AAS)练习巩固3: 如图,O是AB的中点,∠A= ∠B, △AOC与△BOD全等吗?为什么?小明两角和夹边对应相等(已知)(中点的定义)(对顶角相等)解:在 中4: 如图,O是AB的中点,∠C= ∠D, △AOC与△BOD全等吗?为什么?小明两角和一角的对边对应相等(已知)(中点的定义)(对顶角相等)解:在 中∠C= ∠D(AAS)5.已知 和 中, = ,AB=AC.求证: (1) (3) BD=CE证明: (2) AE=AD (全等三角形对应边相等)(已知)(已知)(公共角)(已知)(等式的性质) 6. 如图,已知∠ACB=∠DBC,∠ABC=∠CDB,判别
下面的两个三角形是否全等,并说明理由. 不全等,因为BC虽然是公共边,但不是对应边.提高练习1.如图,HI∥BJ,JI∥BH,求证:△BIH≌△IBJ。证明:∵HI∥BJ,JI∥BH,∴∠HIB=∠JBI,∠HBI=∠JIB,在△BIH和△IBJ中,∠HIB=∠JBI BI=IB ∠HBI=∠JIB ∴△BIH≌△IBJ(ASA)在 和 中2. 如图,AD = AE, ∠B = ∠C ,那么BE与CD相等吗?为什么?两角和其中一角的对应边对应相等(已知)(公共角)(已知)△ABE△ACD∠B = ∠C ∠A = ∠A AE= AD∴ △ABE≌△ACD(AAS)∴ BE=CD(全等三角形对应边相等)提高练习ABCDE123﹑如图,已知,∠C=∠E,∠1=∠2,AB=AD,△ABC和△ADE全等吗?为什么?解: △ABC和△ADE全等。
∵∠1=∠2(已知)
∴∠1+∠DAC=∠2+∠DAC
即∠BAC=∠DAE
在△ABC和△ADC 中 ∴ △ABC≌△ADE(AAS)我的感悟与收获课堂小结 两角和它们的夹边对应相等的两个三角形全等,简写成“角边角”或“ASA”. 两角和其中一角的对边对应相等的两个三角形全等,简写成“角角边”或“AAS”.知识巩固1.如图,已知:∠A=∠D,要使△ABC≌△DCB,只需增加一个条件是( )
A.AC=DB B.BC=CB
C.∠ABC=∠DCB D.AB=DC C根据已知结合图形及判定方法选择条件知识巩固2.求证:在两个锐角三角形中,如果有两角及其中一角的对边上的高对应相等,那么这两个三角形全等。如图所示:已知:在△ABC和△DEF中,∠BAC=∠EDF,∠B=∠E,AM、DN分别是△ABC和△DEF的高,且AM=DN;
求证:△ABC≌△DEF。在△ABM和△DEN中,
∠B=∠E
∠AMB=∠DNE
AM=DN 知识巩固证明:∵AM、DN分别是△ABC和△DEF的高,
∴∠AMB=∠DNE=90°,∴△ABM≌△DEN(AAS),
∴AB=DE,在△ABC和△DEF中,
∠BAC=∠EDF
AB=DE
∠B=∠E
∴△ABC≌△DEF(ASA).知识巩固3.如图,AD∥BC,∠A=∠DEC=90°,DE=EC,试说明AD+BC=AB。再创辉煌:1、如图∠ACB=∠DFE,BC=EF,根据ASA或AAS,那么应补充一个直接条件 --------------------------,(写出一个即可),才能使△ABC≌△DEF2、如图,BE=CD,∠1=∠2,则AB=AC吗?为什么?ABCDEF∠B=∠E或∠A=∠D如图,AB∥CD,AD∥BC,那么AB=CD吗?为什么?AD与BC呢?五、思考题知识巩固证明:∵∠DEC=∠A=90°,
∴∠ADE+∠AED=90°,∠AED+∠BEC=90°,∴∠ADE=∠BEC,
∵AD∥BC,∠A=90°,∴∠B+∠A=180°,∴∠B=∠A=90°,
在△AED和△CEB中,
∠A=∠B
∠ADE=∠BEC
DE=EC ,
∴△AED≌△CEB,∴AE=BC,BE=AD,
∵AE+BE=AB,∴AD+BC=AB..如图,小明不慎将一块三角形模具打碎为三块,他是
否可以只带其中的一块碎片到商店去,就能配一块与
原来一样的三角形模具吗? 如果可以,带哪块去合
适?你能说明其中理由吗?答:带1去,因为有两角且夹边相等的两个三角形全等.知识的升华作业布置:
习题4.7老师期望:
做完题目后,一定要“悟”到点东西,纳入到自己的认知结构中去. 寄语: 亲:
只有不断的思考,才会有新的发现;只有量的变化,才会有质的进步.祝大家学有所得!
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
