10.2 平行线的判定(2)同步练习
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
10.2 平行线的判定(2)同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行 , 简单地说:同位角相等,两直线平行 .
2.两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行,简单地说:内错角相等,两直线平行 .
3.两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行,简单地说:同旁内角互补,两直线平行 .
基础知识和能力拓展精练
一、选择题
1.如图,给出了过直线AB外一点P,作已知直线AB的平行线的方法,其依据是( )
A. 同位角相等,两直线平行 B. 内错角相等,两直线平行
C. 同旁内角互补,两直线品行 D. 过直线外一点有且只有一条直线与这条直线平行
2.已知如图直线a,b被直线c所截,下列条件能判断a∥b的是( )
A. ∠1=∠2 B. ∠2=∠3 C. ∠1=∠4 D. ∠2+∠5=180°
3.已知是任一点,过点P画一条直线与OA平行,则这样的直线( )
A. 有且仅有一条 B. 有两条 C. 不存在 D. 有一条或不存在
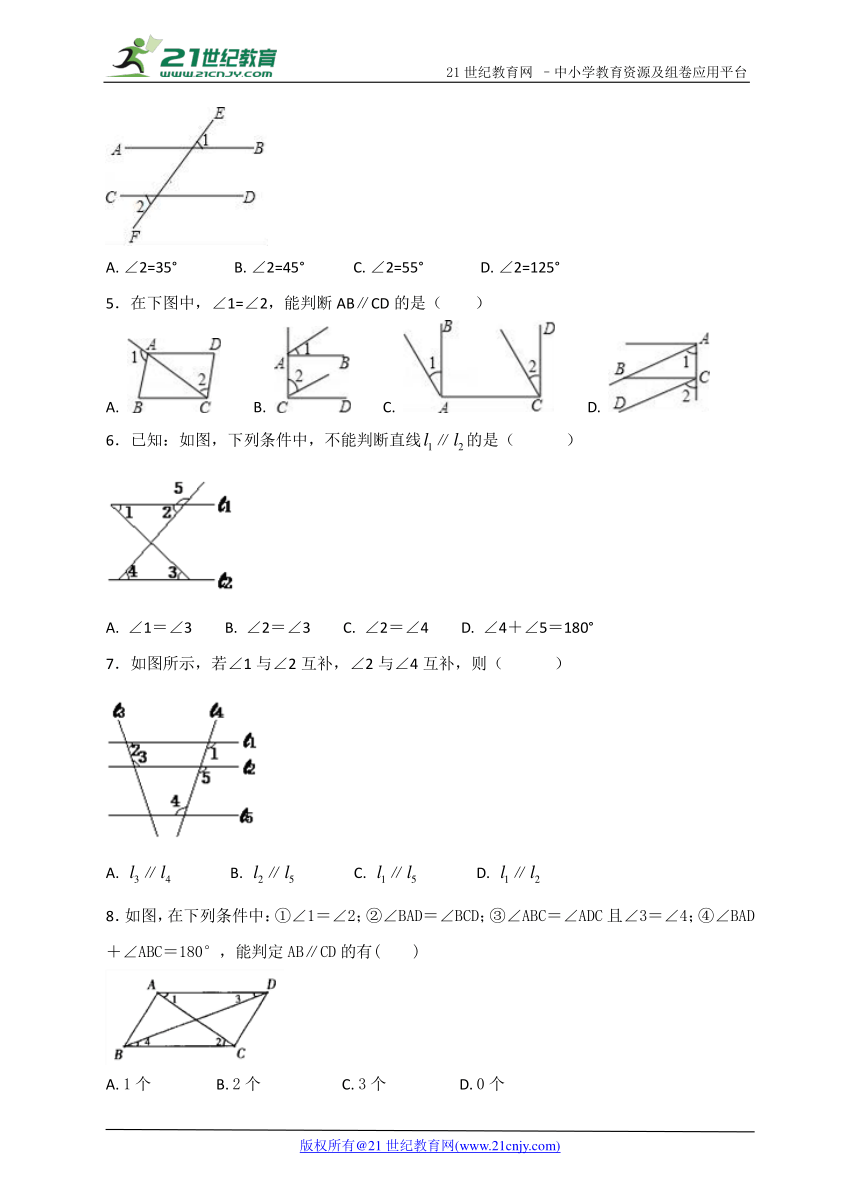
4.如图,直线AB,CD被直线EF所截,∠1=55°,下列条件中能判定AB∥CD的是( )
A. ∠2=35° B. ∠2=45° C. ∠2=55° D. ∠2=125°
5.在下图中,∠1=∠2,能判断AB∥CD的是( )
A. B. C. D.
6.已知:如图,下列条件中,不能判断直线∥的是( )
A. ∠1=∠3 B. ∠2=∠3 C. ∠2=∠4 D. ∠4+∠5=180°
7.如图所示,若∠1与∠2互补,∠2与∠4互补,则( )
A. ∥ B. ∥ C. ∥ D. ∥
8.如图,在下列条件中:①∠1=∠2;②∠BAD=∠BCD;③∠ABC=∠ADC且∠3=∠4;④∠BAD+∠ABC=180°,能判定AB∥CD的有( )
A. 1个 B. 2个 C. 3个 D. 0个
二、填空题
9.如图,已知点B,C,E在一直线上,如果∠1=∠B,那么________∥________.
10.如图,直线a,b与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°; ④∠5+∠3=180°,其中能判断a//b的是______(填序号).
11.如图,已知直线a,b,c,d,e,且∠1=∠2,∠3=∠4,则a与c平行吗 为什么
解:a与c平行;
理由:因为∠1=∠2(____)
所以a//b(_______________)
因为∠3=∠4 (________)
所以b//c(_____________)
所以a//c(_____________)
12.如图,(1)如果∠1=__________,那么DE∥AC;(同位角相等,两直线平行);
(2)如果∠1=__________,那么EF∥BC;(内错角相等,两直线平行);
(3)如果∠DEF+__________=180°,那么DE∥AC;(同旁内角互补,两直线平行);
(4)如果∠2+__________=180°,那么AB∥DF;(同旁内角互补,两直线平行).
13.如图,直线l1∥l2,∠α=∠β,∠1=50°,则∠2=______
14.如图,∠4+∠ADC =1800,且∠1=∠2,说明DG∥AB的理由。
解:∵∠4+∠ADC =1800 (已知)
∠4+∠5 =1800 (平角定义)
∴ ∠5 =________ ( )
∴ _____∥______ (_________________________)
∴ ∠1=_____ (___________________________)
又∵ ∠1=∠2 (已知)
∴ ∠3 =______ (等量代换)
∴ DG∥AB (____________________________)
三、解答题
15.如图,已知AC⊥AE,BD⊥BF,∠1=25°,∠2=25°,AE与BF平行吗?为什么?
16.如图,∠1=30°,∠B=60°,AB⊥AC.
(1)∠DAB+∠B等于多少度?(2)AD与BC平行吗?AB与CD平行吗?
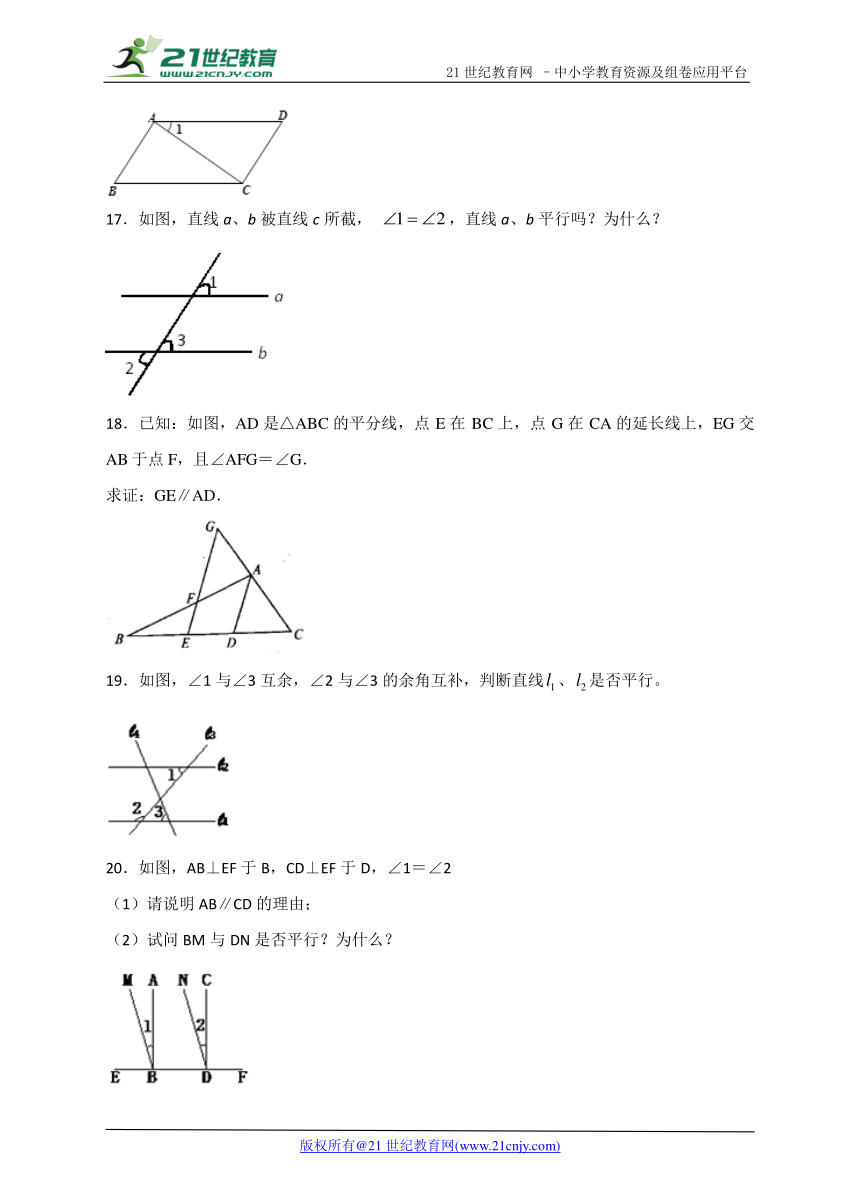
17.如图,直线a、b被直线c所截, ,直线a、b平行吗?为什么?
18.已知:如图,AD是△ABC的平分线,点E在BC上,点G在CA的延长线上,EG交AB于点F,且∠AFG=∠G.
求证:GE∥AD.
19.如图,∠1与∠3互余,∠2与∠3的余角互补,判断直线、是否平行。
20.如图,AB⊥EF于B,CD⊥EF于D,∠1=∠2
(1)请说明AB∥CD的理由;
(2)试问BM与DN是否平行?为什么?
参考答案
1.A
【解析】分析:由平行线的画法可知,∠2与∠1相等,根据图形判断出∠2与∠1的位置关系,由此可得答案.
详解:由平行线的画法可知,∠2与∠1相等,且∠2与∠1是一对同位角,所以画法的依据是:同位角相等,两直线平行.
故选A.
点睛:本题考查的是平行线的原理,熟练掌握平行线的判定方法是解答本题的关键.
2.A
【解析】试题解析:∵∠1=∠2,
∴a∥b;
故选A.
3.D
【解析】试题解析:①若点P在OA上,则不能画出与OA平行的直线,
②若点P不在OA上,则过点P有且只有一条直线与OA平行,
所以,这样的直线有一条或不存在.
故选:D.
4.C
【解析】试题分析:A、由∠3=∠2=35°,∠1=55°推知∠1≠∠3,故不能判定AB∥CD,故本选项错误;
B、由∠3=∠2=45°,∠1=55°推知∠1≠∠3,故不能判定AB∥CD,故本选项错误;
C、由∠3=∠2=55°,∠1=55°推知∠1=∠3,故能判定AB∥CD,故本选项正确;
D、由∠3=∠2=125°,∠1=55°推知∠1≠∠3,故不能判定AB∥CD,故本选项错误;
故选:C.
点睛:本题考查了平行线的判定定理,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
5.D
【解析】试题解析:选项A、B、C中的∠1与∠2都不是直线AB、CD形成的同位角,所以不能判断AB∥CD.
选项D∠1与∠2是直线AB、CD被直线AC所截形成的同位角,所以能判断AB∥CD.
∵∠1=∠2,
∴AB∥CD(同位角相等,两直线平行).
故选D.
【点睛】正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
6.B
【解析】解:当∠1=∠3时, ∥,故A正确;
当∠2=∠3时,不能得出∥,故B错误;
当∠2=∠4时, ∥,故C正确;
当∠4+∠5=180°时.∵∠2+∠5=180°,∴∠2=∠4,∴∥,故D正确.
故选B.
点睛:本题考查了平行线的判定:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
7.C
【解析】解:∵∠1与∠2互补,∠2与∠4互补,∴∠1=∠4(同角的补角相等),∴l1∥l5(内错角相等,两直线平行).故选C.
8.A
【解析】①由∠1=∠2,得到AD∥BC,本选项不合题意;
②由∠BAD=∠BCD,不能判定出平行,本选项不合题意;
③由∠ABC=∠ADC且∠3=∠4,得到∠ABC-∠4=∠ADC-∠3,即∠ABD=∠CDB,得到AB∥CD,本选项符合题意;
④由∠BAD+∠ABC=180°,得到AD∥BC,本选项不合题意;
所以符合题意的只有1个.
故选:A.
【点睛】考查了平行线的判定,熟练掌握平行线的判定方法是解本题的关键.
9. DC , AB
【解析】试题解析:∵∠1=∠B,
∴DC∥AB,
故答案为:DC;AB.
10.①③④
【解析】试题解析:①∵∠1=∠2,
∴a∥b,故此选项正确;
②∠3=∠6无法得出a∥b,故此选项错误;
③∵∠4+∠7=180°,
∴a∥b,故此选项正确;
④∵∠5+∠3=180°,
∴∠2+∠5=180°,
∴a∥b,故此选项正确;
故答案为:①③④.
11.已知 同位角相等,两直线平行 已知 同位角相等,两直线平行 平行于同一条直线的两条直线平行
【解析】a∥c,理由如下:
∵∠1=∠2(已知),
∴a//b(同位角相等,两直线平行),
∵∠3=∠4 (已知),
∴b//c(同位角相等,两直线平行),
∴a//c(平行于同一条直线的两条直线平行).
故答案为已知;同位角相等,两直线平行;已知;同位角相等,两直线平行;平行于同一条直线的两条直线平行.
点睛:掌握平行线的性质和判定定理.
12. ∠C; ∠DEF; ∠EFC; ∠AED.
【解析】(1)如果∠1=∠C ,那么DE//AC;(同位角相等,两直线平行)
(2)如果∠1=∠DEF ,那么EF//BC;(内错角相等,两直线平行)
(3)如果∠DEF+∠EFC =180°,那么DE//AC;(同旁内角互补,两直线平行)
(4)如果∠2+∠AED =180°,,那么AB//DF;(同旁内角互补,两直线平行)
13.130°
【解析】试题解析:如图,
∵l1∥l2,
∴∠3=∠1=50°,
∵∠α=∠β,
∴AB∥CD,
∴∠2+∠3=180°,
∴∠2=180°-∠3=180°-50°=130°.
14.答案见解析
【解析】∠ADC; 同角的补角相等; EF∥AD;
同位角相等,两直线平行;∠3;两直线平行,同位角相等;∠2;内错角相等,两直线平行
15.AE∥BF,理由见解析.
【解析】分析:根据平行得出∠EAC=∠FBD=90°,结合∠1=∠2得出∠EAG=∠FBG,根据平行线的判定定理得出平行.
详解:解:AE∥BF
理由如下:∵AC⊥AE,BD⊥BF,∴∠EAC=∠FBD=90°,又∵∠1=25°,∠2=25°
∴∠EAG=∠FBG=115° , ∴AE∥BF.
点睛:本题主要考查的就是平行线的判定定理,属于基础题型.解决这个问题的关键就是找出同位角,根据垂直得出相等.
16.解:(1)180°;(2)无法确定AB与CD的关系.
【解析】分析:(1)由已知可求得∠DAB=120°,从而可求得∠DAB+∠B=180°;
(2)根据同旁内角互补两直线平行可得AD∥BC,∠ACD不能确定从而不能确定AB与CD平行.
详解:①∵AB⊥AC,∴∠BAC=90°.
又∠1=30°,∴∠BAD=120°.
∵∠B=60°,∴∠DAB+∠B=180°.
②答:AD∥BC,AB与CD不一定平行.理由是:
∵∠DAB+∠B=180°
∴AD∥BC
∵∠ACD不能确定,
∴AB与CD不一定平行.
点睛:本题主要考查学生对平行线的判定的理解及运用.
17.a∥b,理由见解析.
【解析】试题分析:根据同位角相等,两直线平行即可判定.
试题解析:结论:a∥b,
理由:∵∠1=∠2,
∠2=∠3,
∴∠1=∠3 ,
∴a∥b.
18.见解析
【解析】试题分析:首先根据角平分线的性质可得∠BAC=2∠DAC,再根据三角形外角与内角的关系可得∠G+∠GFA=∠BAC,又∠AFG=∠G.进而得到∠BAC=2∠G,从而得到∠DAC=∠G,即可判定出GE∥AD.
试题解析:证明:∵AD是∠CAB的平分线,
∴∠BAC=2∠DAC,
∵∠G+∠GFA=∠BAC,∠AFG=∠G.
∴∠BAC=2∠G,
∴∠DAC=∠G,
∴AD∥GE.
19.∥,(提示:证明∠1+∠2=180°)
【解析】试题分析:同位角的余角相等可得到∠1+∠2=180°,根据平行线的判定可得到结论.
试题解析:解:平行,理由如下:
∵∠1与∠3互余,∴∠1是∠3的余角.∵∠2与∠3的余角互补,∴∠1+∠2=180°,∴∥.
点睛:本题主要考查平行线的判定,掌握两直线平行的判定方法是解题的关键,即①同位角相等 两直线平行,②内错角相等 两直线平行,③同旁内角互补 两直线平行.
20.证明见解析
【解析】试题分析:(1)直接根据平行线的性质即可得出结论;
(2)先根据AB⊥EF于点B,CD⊥EF于点D得出∠ABE=∠CDE,再由∠1=∠2可知∠MBE=∠NDE,由此可得出结论.
试题解析:(1)证明:∵AB⊥EF于点B,CD⊥EF于点D,∴∠ABE=∠CDE=90°,∴AB∥CD;
(2)BM∥DN.理由如下:
∵AB⊥EF于点B,CD⊥EF于点D,∴∠ABE=∠CDE.
∵∠1=∠2,∴∠MBE=∠NDE,∴BM∥DN.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
10.2 平行线的判定(2)同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行 , 简单地说:同位角相等,两直线平行 .
2.两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行,简单地说:内错角相等,两直线平行 .
3.两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行,简单地说:同旁内角互补,两直线平行 .
基础知识和能力拓展精练
一、选择题
1.如图,给出了过直线AB外一点P,作已知直线AB的平行线的方法,其依据是( )
A. 同位角相等,两直线平行 B. 内错角相等,两直线平行
C. 同旁内角互补,两直线品行 D. 过直线外一点有且只有一条直线与这条直线平行
2.已知如图直线a,b被直线c所截,下列条件能判断a∥b的是( )
A. ∠1=∠2 B. ∠2=∠3 C. ∠1=∠4 D. ∠2+∠5=180°
3.已知是任一点,过点P画一条直线与OA平行,则这样的直线( )
A. 有且仅有一条 B. 有两条 C. 不存在 D. 有一条或不存在
4.如图,直线AB,CD被直线EF所截,∠1=55°,下列条件中能判定AB∥CD的是( )
A. ∠2=35° B. ∠2=45° C. ∠2=55° D. ∠2=125°
5.在下图中,∠1=∠2,能判断AB∥CD的是( )
A. B. C. D.
6.已知:如图,下列条件中,不能判断直线∥的是( )
A. ∠1=∠3 B. ∠2=∠3 C. ∠2=∠4 D. ∠4+∠5=180°
7.如图所示,若∠1与∠2互补,∠2与∠4互补,则( )
A. ∥ B. ∥ C. ∥ D. ∥
8.如图,在下列条件中:①∠1=∠2;②∠BAD=∠BCD;③∠ABC=∠ADC且∠3=∠4;④∠BAD+∠ABC=180°,能判定AB∥CD的有( )
A. 1个 B. 2个 C. 3个 D. 0个
二、填空题
9.如图,已知点B,C,E在一直线上,如果∠1=∠B,那么________∥________.
10.如图,直线a,b与直线c相交,给出下列条件:①∠1=∠2;②∠3=∠6;③∠4+∠7=180°; ④∠5+∠3=180°,其中能判断a//b的是______(填序号).
11.如图,已知直线a,b,c,d,e,且∠1=∠2,∠3=∠4,则a与c平行吗 为什么
解:a与c平行;
理由:因为∠1=∠2(____)
所以a//b(_______________)
因为∠3=∠4 (________)
所以b//c(_____________)
所以a//c(_____________)
12.如图,(1)如果∠1=__________,那么DE∥AC;(同位角相等,两直线平行);
(2)如果∠1=__________,那么EF∥BC;(内错角相等,两直线平行);
(3)如果∠DEF+__________=180°,那么DE∥AC;(同旁内角互补,两直线平行);
(4)如果∠2+__________=180°,那么AB∥DF;(同旁内角互补,两直线平行).
13.如图,直线l1∥l2,∠α=∠β,∠1=50°,则∠2=______
14.如图,∠4+∠ADC =1800,且∠1=∠2,说明DG∥AB的理由。
解:∵∠4+∠ADC =1800 (已知)
∠4+∠5 =1800 (平角定义)
∴ ∠5 =________ ( )
∴ _____∥______ (_________________________)
∴ ∠1=_____ (___________________________)
又∵ ∠1=∠2 (已知)
∴ ∠3 =______ (等量代换)
∴ DG∥AB (____________________________)
三、解答题
15.如图,已知AC⊥AE,BD⊥BF,∠1=25°,∠2=25°,AE与BF平行吗?为什么?
16.如图,∠1=30°,∠B=60°,AB⊥AC.
(1)∠DAB+∠B等于多少度?(2)AD与BC平行吗?AB与CD平行吗?
17.如图,直线a、b被直线c所截, ,直线a、b平行吗?为什么?
18.已知:如图,AD是△ABC的平分线,点E在BC上,点G在CA的延长线上,EG交AB于点F,且∠AFG=∠G.
求证:GE∥AD.
19.如图,∠1与∠3互余,∠2与∠3的余角互补,判断直线、是否平行。
20.如图,AB⊥EF于B,CD⊥EF于D,∠1=∠2
(1)请说明AB∥CD的理由;
(2)试问BM与DN是否平行?为什么?
参考答案
1.A
【解析】分析:由平行线的画法可知,∠2与∠1相等,根据图形判断出∠2与∠1的位置关系,由此可得答案.
详解:由平行线的画法可知,∠2与∠1相等,且∠2与∠1是一对同位角,所以画法的依据是:同位角相等,两直线平行.
故选A.
点睛:本题考查的是平行线的原理,熟练掌握平行线的判定方法是解答本题的关键.
2.A
【解析】试题解析:∵∠1=∠2,
∴a∥b;
故选A.
3.D
【解析】试题解析:①若点P在OA上,则不能画出与OA平行的直线,
②若点P不在OA上,则过点P有且只有一条直线与OA平行,
所以,这样的直线有一条或不存在.
故选:D.
4.C
【解析】试题分析:A、由∠3=∠2=35°,∠1=55°推知∠1≠∠3,故不能判定AB∥CD,故本选项错误;
B、由∠3=∠2=45°,∠1=55°推知∠1≠∠3,故不能判定AB∥CD,故本选项错误;
C、由∠3=∠2=55°,∠1=55°推知∠1=∠3,故能判定AB∥CD,故本选项正确;
D、由∠3=∠2=125°,∠1=55°推知∠1≠∠3,故不能判定AB∥CD,故本选项错误;
故选:C.
点睛:本题考查了平行线的判定定理,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
5.D
【解析】试题解析:选项A、B、C中的∠1与∠2都不是直线AB、CD形成的同位角,所以不能判断AB∥CD.
选项D∠1与∠2是直线AB、CD被直线AC所截形成的同位角,所以能判断AB∥CD.
∵∠1=∠2,
∴AB∥CD(同位角相等,两直线平行).
故选D.
【点睛】正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
6.B
【解析】解:当∠1=∠3时, ∥,故A正确;
当∠2=∠3时,不能得出∥,故B错误;
当∠2=∠4时, ∥,故C正确;
当∠4+∠5=180°时.∵∠2+∠5=180°,∴∠2=∠4,∴∥,故D正确.
故选B.
点睛:本题考查了平行线的判定:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
7.C
【解析】解:∵∠1与∠2互补,∠2与∠4互补,∴∠1=∠4(同角的补角相等),∴l1∥l5(内错角相等,两直线平行).故选C.
8.A
【解析】①由∠1=∠2,得到AD∥BC,本选项不合题意;
②由∠BAD=∠BCD,不能判定出平行,本选项不合题意;
③由∠ABC=∠ADC且∠3=∠4,得到∠ABC-∠4=∠ADC-∠3,即∠ABD=∠CDB,得到AB∥CD,本选项符合题意;
④由∠BAD+∠ABC=180°,得到AD∥BC,本选项不合题意;
所以符合题意的只有1个.
故选:A.
【点睛】考查了平行线的判定,熟练掌握平行线的判定方法是解本题的关键.
9. DC , AB
【解析】试题解析:∵∠1=∠B,
∴DC∥AB,
故答案为:DC;AB.
10.①③④
【解析】试题解析:①∵∠1=∠2,
∴a∥b,故此选项正确;
②∠3=∠6无法得出a∥b,故此选项错误;
③∵∠4+∠7=180°,
∴a∥b,故此选项正确;
④∵∠5+∠3=180°,
∴∠2+∠5=180°,
∴a∥b,故此选项正确;
故答案为:①③④.
11.已知 同位角相等,两直线平行 已知 同位角相等,两直线平行 平行于同一条直线的两条直线平行
【解析】a∥c,理由如下:
∵∠1=∠2(已知),
∴a//b(同位角相等,两直线平行),
∵∠3=∠4 (已知),
∴b//c(同位角相等,两直线平行),
∴a//c(平行于同一条直线的两条直线平行).
故答案为已知;同位角相等,两直线平行;已知;同位角相等,两直线平行;平行于同一条直线的两条直线平行.
点睛:掌握平行线的性质和判定定理.
12. ∠C; ∠DEF; ∠EFC; ∠AED.
【解析】(1)如果∠1=∠C ,那么DE//AC;(同位角相等,两直线平行)
(2)如果∠1=∠DEF ,那么EF//BC;(内错角相等,两直线平行)
(3)如果∠DEF+∠EFC =180°,那么DE//AC;(同旁内角互补,两直线平行)
(4)如果∠2+∠AED =180°,,那么AB//DF;(同旁内角互补,两直线平行)
13.130°
【解析】试题解析:如图,
∵l1∥l2,
∴∠3=∠1=50°,
∵∠α=∠β,
∴AB∥CD,
∴∠2+∠3=180°,
∴∠2=180°-∠3=180°-50°=130°.
14.答案见解析
【解析】∠ADC; 同角的补角相等; EF∥AD;
同位角相等,两直线平行;∠3;两直线平行,同位角相等;∠2;内错角相等,两直线平行
15.AE∥BF,理由见解析.
【解析】分析:根据平行得出∠EAC=∠FBD=90°,结合∠1=∠2得出∠EAG=∠FBG,根据平行线的判定定理得出平行.
详解:解:AE∥BF
理由如下:∵AC⊥AE,BD⊥BF,∴∠EAC=∠FBD=90°,又∵∠1=25°,∠2=25°
∴∠EAG=∠FBG=115° , ∴AE∥BF.
点睛:本题主要考查的就是平行线的判定定理,属于基础题型.解决这个问题的关键就是找出同位角,根据垂直得出相等.
16.解:(1)180°;(2)无法确定AB与CD的关系.
【解析】分析:(1)由已知可求得∠DAB=120°,从而可求得∠DAB+∠B=180°;
(2)根据同旁内角互补两直线平行可得AD∥BC,∠ACD不能确定从而不能确定AB与CD平行.
详解:①∵AB⊥AC,∴∠BAC=90°.
又∠1=30°,∴∠BAD=120°.
∵∠B=60°,∴∠DAB+∠B=180°.
②答:AD∥BC,AB与CD不一定平行.理由是:
∵∠DAB+∠B=180°
∴AD∥BC
∵∠ACD不能确定,
∴AB与CD不一定平行.
点睛:本题主要考查学生对平行线的判定的理解及运用.
17.a∥b,理由见解析.
【解析】试题分析:根据同位角相等,两直线平行即可判定.
试题解析:结论:a∥b,
理由:∵∠1=∠2,
∠2=∠3,
∴∠1=∠3 ,
∴a∥b.
18.见解析
【解析】试题分析:首先根据角平分线的性质可得∠BAC=2∠DAC,再根据三角形外角与内角的关系可得∠G+∠GFA=∠BAC,又∠AFG=∠G.进而得到∠BAC=2∠G,从而得到∠DAC=∠G,即可判定出GE∥AD.
试题解析:证明:∵AD是∠CAB的平分线,
∴∠BAC=2∠DAC,
∵∠G+∠GFA=∠BAC,∠AFG=∠G.
∴∠BAC=2∠G,
∴∠DAC=∠G,
∴AD∥GE.
19.∥,(提示:证明∠1+∠2=180°)
【解析】试题分析:同位角的余角相等可得到∠1+∠2=180°,根据平行线的判定可得到结论.
试题解析:解:平行,理由如下:
∵∠1与∠3互余,∴∠1是∠3的余角.∵∠2与∠3的余角互补,∴∠1+∠2=180°,∴∥.
点睛:本题主要考查平行线的判定,掌握两直线平行的判定方法是解题的关键,即①同位角相等 两直线平行,②内错角相等 两直线平行,③同旁内角互补 两直线平行.
20.证明见解析
【解析】试题分析:(1)直接根据平行线的性质即可得出结论;
(2)先根据AB⊥EF于点B,CD⊥EF于点D得出∠ABE=∠CDE,再由∠1=∠2可知∠MBE=∠NDE,由此可得出结论.
试题解析:(1)证明:∵AB⊥EF于点B,CD⊥EF于点D,∴∠ABE=∠CDE=90°,∴AB∥CD;
(2)BM∥DN.理由如下:
∵AB⊥EF于点B,CD⊥EF于点D,∴∠ABE=∠CDE.
∵∠1=∠2,∴∠MBE=∠NDE,∴BM∥DN.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
