10.4 平移同步练习
图片预览


文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
10.4 平移同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.在平面内,一个图形沿某个方向移动一定的距离,这种图形的变换叫做平移.平移时,原图形上的所有点都沿同一个方向移动相同的距离,原图 形上一点A平移后成为点A′,这样的两点叫做对应点 .
2.(1)平移只改变 图形的位置,不改变图形的形状和大小 .
(2)平移后的图形与原来的图形的对应线段 平行且相等,对应角相等,图形的形状与大小都 没有发生变化.
(3)对应点所连的线段平行且相等 .
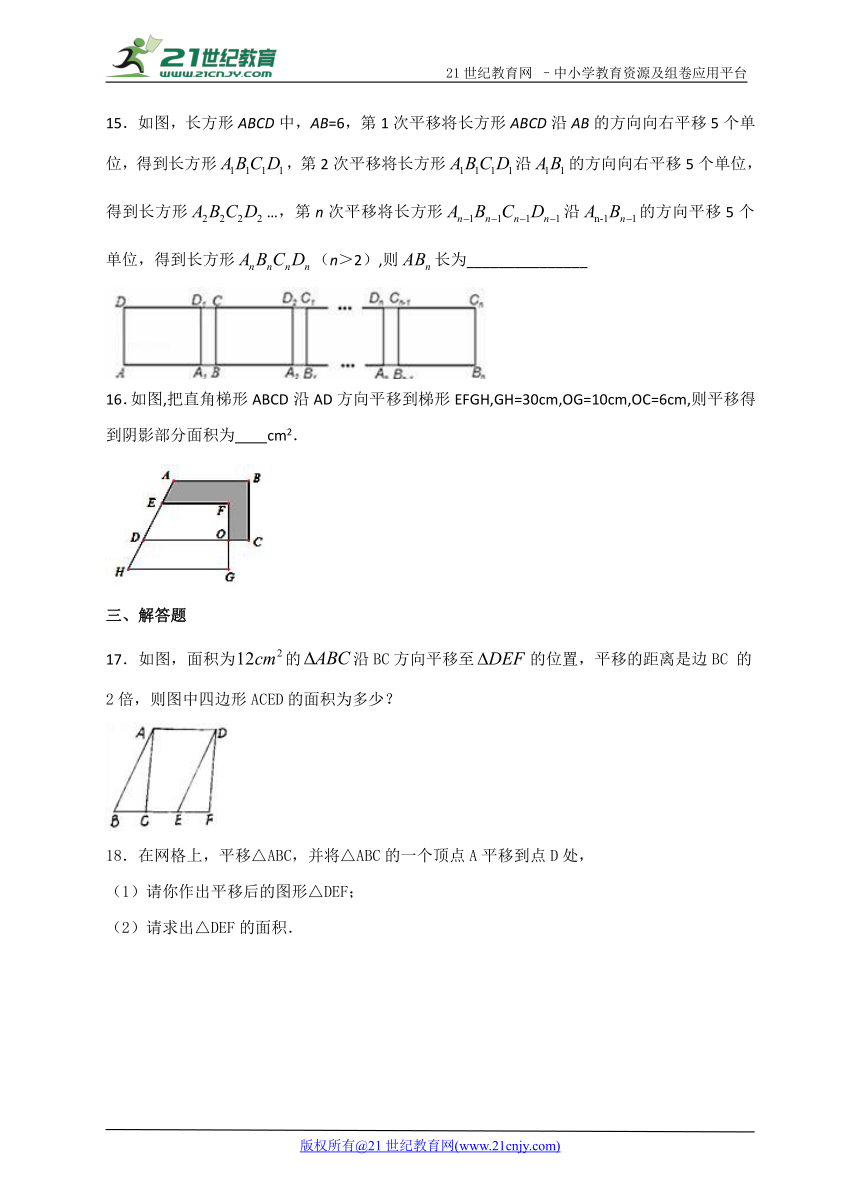
基础知识和能力拓展精练
一、选择题
1.下列各现象中:①电梯的升降,②照镜子,③钟表分针的运动,④行驶中汽车车轮的运动,其中是平移现象的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
2.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( )
A. 42 B. 96 C. 84 D. 48
3.如图,将△ABC沿AB方向平移至△DEF,且AB=5,DB=2,则CF的长度为( )
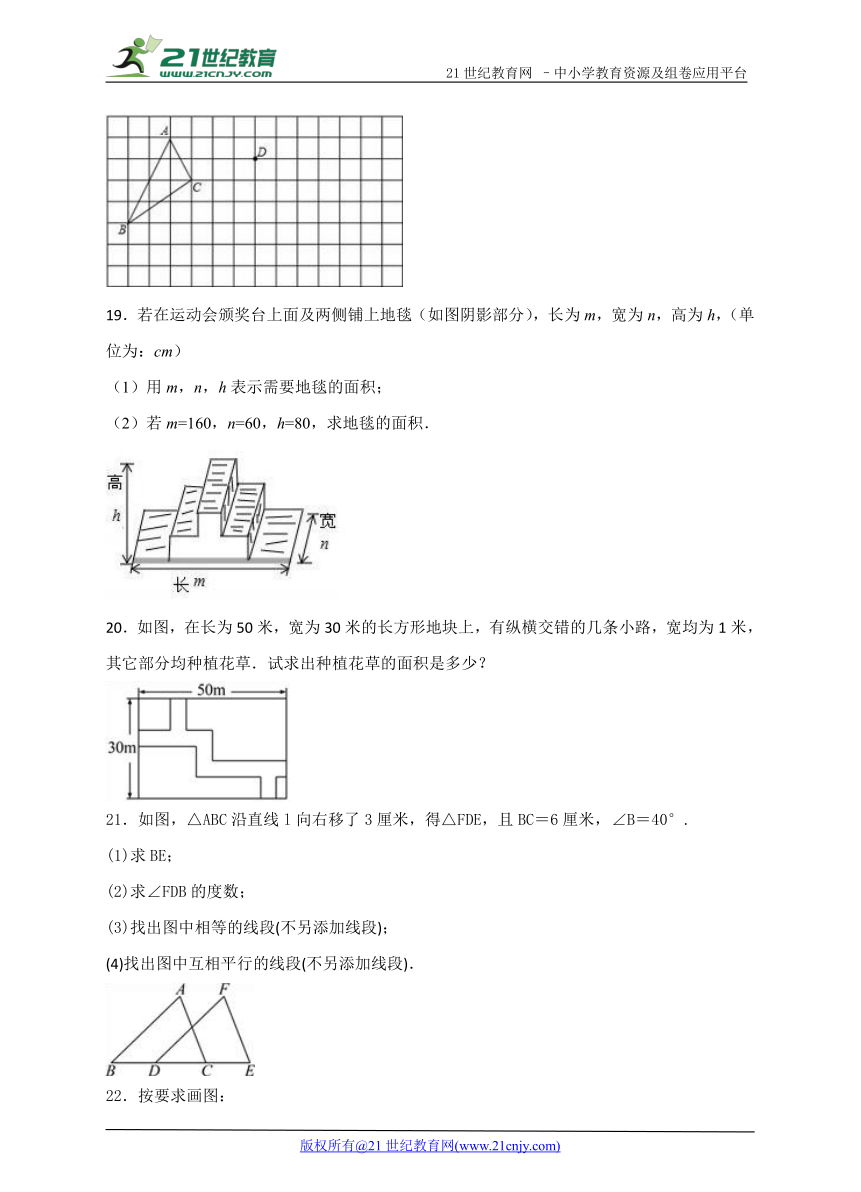
A. 5 B. 3 C. 2 D. 1
4.通过平移得到的新图形中的每一点与原图形中的对应点的连线( )
A. 平行 B. 相等 C. 共线 D. 平行(或共线)且相等
5.如图,在5×5的方格纸中将图①中的图形N平移到如图②所示的位置,那么下列平移正确的是( )
A. 先向下移动1格,再向左移动1格 B. 先向下移动1格,再向左移动2格
C. 先向下移动2格,再向左移动1格 D. 先向下移动2格,再向左移动2格
6.如图所示的图案是一些汽车的车标,可以看作由“基本图案”经过平移得到的是( )
A. B. C. D.
7.如图,△DEF是由△ABC平移得到,且点B、E、C、F在同一直线上,若BF=14,CE=6,则BE的长度为( )
A. 2 B. 3 C. 4 D. 5
8.如图,两只蚂蚁以相同的速度沿两条不同的路径,同时从A出发爬到B,则( )
A. 乙比甲先到 B. 甲比乙先到 C. 甲和乙同时到 D. 无法确定
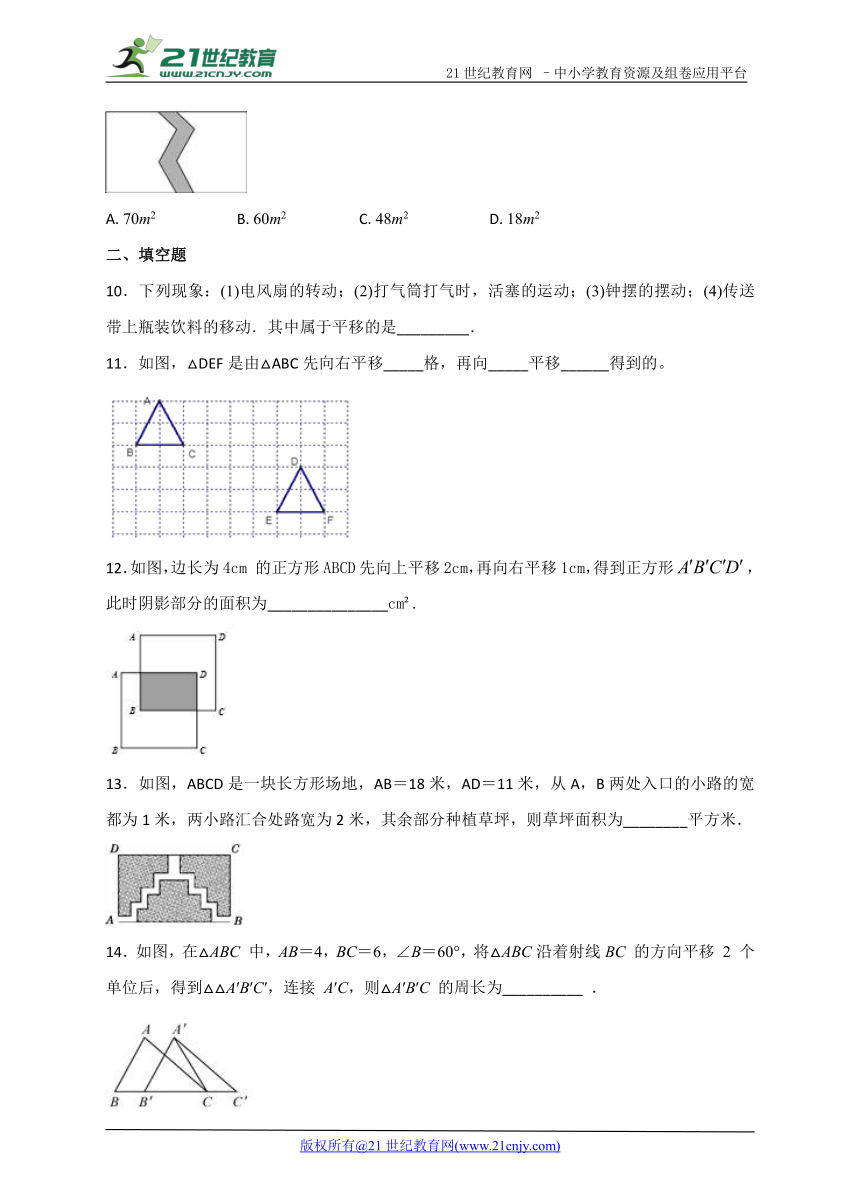
9.如图,在一块长为12m,宽为6m的长方形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是2m),则空白部分表示的草地面积是 ( )
A. 70m2 B. 60m2 C. 48m2 D. 18m2
二、填空题
10.下列现象:(1)电风扇的转动;(2)打气筒打气时,活塞的运动;(3)钟摆的摆动;(4)传送带上瓶装饮料的移动.其中属于平移的是_________.
11.如图,△DEF是由△ABC先向右平移_____格,再向_____平移______得到的。
12.如图,边长为4cm 的正方形ABCD先向上平移2cm,再向右平移1cm,得到正方形,此时阴影部分的面积为_______________cm .
13.如图,ABCD是一块长方形场地,AB=18米,AD=11米,从A,B两处入口的小路的宽都为1米,两小路汇合处路宽为2米,其余部分种植草坪,则草坪面积为________平方米.
14.如图,在△ABC 中,AB=4,BC=6,∠B=60°,将△ABC沿着射线BC 的方向平移 2 个单位后,得到△△A′B′C′,连接 A′C,则△A′B′C 的周长为__________ .
15.如图,长方形ABCD中,AB=6,第1次平移将长方形ABCD沿AB的方向向右平移5个单位,得到长方形 EMBED Equation.DSMT4 ,第2次平移将长方形沿的方向向右平移5个单位,得到长方形…,第n次平移将长方形沿的方向平移5个单位,得到长方形(n>2),则长为_______________
16.如图,把直角梯形ABCD沿AD方向平移到梯形EFGH,GH=30cm,OG=10cm,OC=6cm,则平移得到阴影部分面积为____cm2.
三、解答题
17.如图,面积为 EMBED Equation.DSMT4 的沿BC方向平移至的位置,平移的距离是边BC 的2倍,则图中四边形ACED的面积为多少?
18.在网格上,平移△ABC,并将△ABC的一个顶点A平移到点D处,
(1)请你作出平移后的图形△DEF;
(2)请求出△DEF的面积.
19.若在运动会颁奖台上面及两侧铺上地毯(如图阴影部分),长为m,宽为n,高为h,(单位为:cm)
(1)用m,n,h表示需要地毯的面积;
(2)若m=160,n=60,h=80,求地毯的面积.
20.如图,在长为50米,宽为30米的长方形地块上,有纵横交错的几条小路,宽均为1米,其它部分均种植花草.试求出种植花草的面积是多少?
21.如图,△ABC沿直线l向右移了3厘米,得△FDE,且BC=6厘米,∠B=40°.
(1)求BE;
(2)求∠FDB的度数;
(3)找出图中相等的线段(不另添加线段);
(4)找出图中互相平行的线段(不另添加线段).
22.按要求画图:
如图1,已知P为直线AB外一点.
过点P作,垂足为D;
过点P作
如图2,平移,使点A移动到点处,画出平移后的.
参考答案
1.A
【解析】分析:判断生活中的现象是否是平移,要根据平移的定义,进行判断,图形平移前后的形状和大小没有变化,只是位置发生变化.
详解:①电梯的升降,是平移;②照镜子,是轴对称;③钟表分针的运动,是旋转;④行驶中汽车车轮的运动,是旋转.故平移现象有1个.故选A.
点睛:本题考查了图形的平移,图形的平移只改变图形的位置,而不改变图形的形状和大小,学生易混淆图形的平移与旋转或翻转而误选.
2.D
【解析】由题意知,BE=6,DE=AB=10,
∴OE=DE-DO=10-4=6,
∴S四边形ODFC=S梯形ABEO= (AB+OE)·BE=×(10+6)×6=48.
故选D.
3.B
【解析】试题解析:∵△ABC沿AB方向平移至△DEF,平移的距离是AD,
∴AD=AB DB=5 2=3,
∴CF=AD=3.
故选B.
4.D
【解析】试题解析:平移,是指在平面内,将一个图形上的所有点都按照某个直线方向做相同距离的移动,这样的图形运动叫做图形的平移运动,简称平移.平移不改变图形的形状和大小. 平移后的图形与原图形上对应点连接的线段平行(或在同一条直线上)且相等.
故选D.
5.C
【解析】试题解析:由方程可知,在5×5方格纸中将图①中的图形N平移后的位置如图②所示,那么下面平移中正确的是:先向下移动2格,再向左移动1格;
故选C.
6.D
【解析】分析:根据平移的性质:不改变图形的形状和大小,不可旋转与翻转,将题中所示的图案通过平移后可以得到的图案是D.
详解:观察图形可知,图案D可以看作由“基本图案”经过平移得到.
故选D.
点睛:本题主要考查了图形的平移,图形的平移只改变图形的位置,而不改变图形的形状和大小,学生易混淆图形的平移与旋转或翻转,而导致错选.
7.C
【解析】∵△DEF是由△ABC通过平移得到,
∴BE=CF,
∴BE= EMBED Equation.DSMT4 (BF-EC),
∵BF=14,EC=6,
∴BE=(14-6)=4.
故选:C.
8.C
【解析】由平移的性质可知,甲、乙两只蚂蚁的行走的路程相同,且两只蚂蚁的速度相同,所以两只蚂蚁同时到达,故选C.
9.B
【解析】草地面积=长方形面积-小路面积=12×6-2×6=60(m2),
故选B.
10.(2)(4)
【解析】试题分析:(1)电风扇的转动是旋转,不属于平移;
(2)打气筒打气时,活塞的运动属于平移;
(3)钟摆的摆动是旋转,不属于平移;
(4)传送带上瓶装饮料的移动符合平移的性质,属于平移.
故选D.
点睛:本题考查图形的平移变换.图形的平移只改变图形的位置,而不改变图形的形状和大小,学生易混淆图形的平移与旋转或翻转,以致选错.
11.6;下;3.
【解析】试题解析:选取A点观察,通过图形信息知将A点向右平移6个单位,再向下平移3个单位可到D点位置,即B点到E点,C点到F点都是同样的平移方法,
△DEF是由△ABC先向右平移6格,再向下平移3格而得到的.
故答案为:6;下;3.
12.6
【解析】阴影部分为长方形,根据平移的性质可得阴影部分是长为3,宽为2,让长乘宽即为阴影部分的面积.
解:易知,当正方形ABCD向上平移2cm。则阴影长方形的宽=4-2=2cm
向右平移1cm则阴影长方形的长=4-1=3cm
所以阴影部分面积=2×3=6cm
“点睛”本题难度较低,主要考查学生对平移知识点的掌握。要注意数形结合思想的培养,运用到考试中去。
13.160
【解析】解:由图可知:矩形ABCD中去掉小路后,草坪正好可以拼成一个新的矩形,且它的长为:(18﹣2)米,宽为(11﹣1)米.所以草坪的面积应该是长×宽=(18﹣2)(11﹣1)=160(米2).故答案为:160.
点睛:本题考查了生活中的平移,根据图形得出草坪正好可以拼成一个长方形是解题的关键.
14.12.
【解析】根据平移性质,判定△A′B′C为等边三角形,然后求解.
解:由题意,得BB′=2,
∴B′C=BC-BB′=4.
由平移性质,可知A′B′=AB=4,∠A′B′C=∠ABC=60°,
∴A′B′=B′C,且∠A′B′C=60°,
∴△A′B′C为等边三角形,
∴△A′B′C的周长=3A′B′=12.
故答案为:12.
“点睛”本题考查的是平移的性质,熟知图形平移后新图形与原图形的形状和大小完全相同是解答此题的关键.
15.6+5n
【解析】每次平移5个单位,n次平移5n个单位,即BN的长为5n,加上AB的长即为ABn的长.
ABn=5n+AB=5n+6.
16.270
【解析】试题解析:由平移的性质,梯形ABCD的面积=梯形EFGH的面积,CD=HG=30cm,
∴阴影部分的面积=梯形DHGO的面积,
∵CO=6cm,
∴DO=CD-CO=30-6=24cm,
∴阴影部分的面积=(DO+HG) OG=(24+30)×10=270cm2.
故答案为:270.
17.36cm2
【解析】试题分析:根据题意得出AD=CF=2BC,EF=BC,则CE=BC,根据面积计算法则得出四边形的面积为△ABC面积的3倍,得出答案.
试题解析:根据题意可得:AD=CF=2BC,EF=BC,则CE=BC
∴四边形的面积=(CE+AD)h×=(BC+2BC)h×=.
18.(1)作图见解析;(2)4.
【解析】试题分析:(1)根据图形平移的性质画出△DEF即可;
(2)利用矩形的面积减去三个顶点上三角形的面积即可.
试题解析:(1)作图如下:
(2)由图可知,S△DEF=3×4﹣ EMBED Equation.DSMT4 ×2×4﹣×2×3﹣×2×1
=12﹣4﹣3﹣1
=4.
19.(1)mn+2nh;(2)19200cm2.
【解析】试题分析:(1)根据平移计算出地毯总长为(m+2h),然后再根据长×宽可得面积;
(2)把已知数据代入(1)中求出答案.
试题解析:
解:(1)地毯的面积为:(m+2h)·n=mn+2nh;
(2)地毯总长:80×2+160=320(cm),
320×60=19200(cm2),
答:地毯的面积为19200cm2.
点睛:此题主要考查了生活中的平移现象、代数式求值,关键是根据平移得出地毯的总长为(m+2h).
20.1421m2
【解析】试题分析:将横向的小路平移至长方形的上边,将纵向小路平移至长方形的左边,则剩余部分即为种植花草的面积.
解:将横向的小路平移至长方形的上边,将纵向小路平移至长方形的左边,如图所示:
所以种植花草的面积=(50-1)(30-1)=1421m2.
点睛:本题考查了平移在实际中的应用,将两条小路平移至长方形的边上,使种植花草的面积等于一个长方形的面积是解决此题的关键.
21. (1) 9厘米;(2) 140°;(3) AB=FD、AC=FE、BC=DE、BD=CE;(4) AB∥FD、AC∥FE.
【解析】试题分析:(1)根据平移的性质可得CE=3cm,然后根据BE=BC+CE即可得出结论;
(2)根据平移的性质得出∠FDE的度数,然后根据邻补角互补即可得出答案;
(3)直接根据平移的性质即可得出结论;
(4)根据平移的性质即可得出结论.
试题解析:
解:(1)∵△ABC沿直线l向右移了3厘米,∴CE=BD=3cm,∴BE=BC+CE=6+3=9厘米;
(2)∵∠FDE=∠B=40°,∴∠FDB=140°;
(3)相等的线段有:AB=FD、AC=FE、BC=DE、BD=CE;
(4)平行的线段有:AB∥FD、AC∥FE.
点睛:本题考查了平移的性质:平移前后的两个图形的对应线段平行且相等;对应角相等;对应点连线平行且相等.
22.答案见解析
【解析】试题分析:(1)①过点P作 垂足为即可;
②利用直尺作PE∥AB即可;
(2)根据图形平移的性质画出平移后的即可.
试题解析: ①如图1所示;
②如图1所示;
如图2所示.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
10.4 平移同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.在平面内,一个图形沿某个方向移动一定的距离,这种图形的变换叫做平移.平移时,原图形上的所有点都沿同一个方向移动相同的距离,原图 形上一点A平移后成为点A′,这样的两点叫做对应点 .
2.(1)平移只改变 图形的位置,不改变图形的形状和大小 .
(2)平移后的图形与原来的图形的对应线段 平行且相等,对应角相等,图形的形状与大小都 没有发生变化.
(3)对应点所连的线段平行且相等 .
基础知识和能力拓展精练
一、选择题
1.下列各现象中:①电梯的升降,②照镜子,③钟表分针的运动,④行驶中汽车车轮的运动,其中是平移现象的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
2.如图,两个全等的直角三角形重叠在一起,将其中的一个三角形沿着点B到C的方向平移到△DEF的位置,AB=10,DO=4,平移距离为6,则阴影部分面积为( )
A. 42 B. 96 C. 84 D. 48
3.如图,将△ABC沿AB方向平移至△DEF,且AB=5,DB=2,则CF的长度为( )
A. 5 B. 3 C. 2 D. 1
4.通过平移得到的新图形中的每一点与原图形中的对应点的连线( )
A. 平行 B. 相等 C. 共线 D. 平行(或共线)且相等
5.如图,在5×5的方格纸中将图①中的图形N平移到如图②所示的位置,那么下列平移正确的是( )
A. 先向下移动1格,再向左移动1格 B. 先向下移动1格,再向左移动2格
C. 先向下移动2格,再向左移动1格 D. 先向下移动2格,再向左移动2格
6.如图所示的图案是一些汽车的车标,可以看作由“基本图案”经过平移得到的是( )
A. B. C. D.
7.如图,△DEF是由△ABC平移得到,且点B、E、C、F在同一直线上,若BF=14,CE=6,则BE的长度为( )
A. 2 B. 3 C. 4 D. 5
8.如图,两只蚂蚁以相同的速度沿两条不同的路径,同时从A出发爬到B,则( )
A. 乙比甲先到 B. 甲比乙先到 C. 甲和乙同时到 D. 无法确定
9.如图,在一块长为12m,宽为6m的长方形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是2m),则空白部分表示的草地面积是 ( )
A. 70m2 B. 60m2 C. 48m2 D. 18m2
二、填空题
10.下列现象:(1)电风扇的转动;(2)打气筒打气时,活塞的运动;(3)钟摆的摆动;(4)传送带上瓶装饮料的移动.其中属于平移的是_________.
11.如图,△DEF是由△ABC先向右平移_____格,再向_____平移______得到的。
12.如图,边长为4cm 的正方形ABCD先向上平移2cm,再向右平移1cm,得到正方形,此时阴影部分的面积为_______________cm .
13.如图,ABCD是一块长方形场地,AB=18米,AD=11米,从A,B两处入口的小路的宽都为1米,两小路汇合处路宽为2米,其余部分种植草坪,则草坪面积为________平方米.
14.如图,在△ABC 中,AB=4,BC=6,∠B=60°,将△ABC沿着射线BC 的方向平移 2 个单位后,得到△△A′B′C′,连接 A′C,则△A′B′C 的周长为__________ .
15.如图,长方形ABCD中,AB=6,第1次平移将长方形ABCD沿AB的方向向右平移5个单位,得到长方形 EMBED Equation.DSMT4 ,第2次平移将长方形沿的方向向右平移5个单位,得到长方形…,第n次平移将长方形沿的方向平移5个单位,得到长方形(n>2),则长为_______________
16.如图,把直角梯形ABCD沿AD方向平移到梯形EFGH,GH=30cm,OG=10cm,OC=6cm,则平移得到阴影部分面积为____cm2.
三、解答题
17.如图,面积为 EMBED Equation.DSMT4 的沿BC方向平移至的位置,平移的距离是边BC 的2倍,则图中四边形ACED的面积为多少?
18.在网格上,平移△ABC,并将△ABC的一个顶点A平移到点D处,
(1)请你作出平移后的图形△DEF;
(2)请求出△DEF的面积.
19.若在运动会颁奖台上面及两侧铺上地毯(如图阴影部分),长为m,宽为n,高为h,(单位为:cm)
(1)用m,n,h表示需要地毯的面积;
(2)若m=160,n=60,h=80,求地毯的面积.
20.如图,在长为50米,宽为30米的长方形地块上,有纵横交错的几条小路,宽均为1米,其它部分均种植花草.试求出种植花草的面积是多少?
21.如图,△ABC沿直线l向右移了3厘米,得△FDE,且BC=6厘米,∠B=40°.
(1)求BE;
(2)求∠FDB的度数;
(3)找出图中相等的线段(不另添加线段);
(4)找出图中互相平行的线段(不另添加线段).
22.按要求画图:
如图1,已知P为直线AB外一点.
过点P作,垂足为D;
过点P作
如图2,平移,使点A移动到点处,画出平移后的.
参考答案
1.A
【解析】分析:判断生活中的现象是否是平移,要根据平移的定义,进行判断,图形平移前后的形状和大小没有变化,只是位置发生变化.
详解:①电梯的升降,是平移;②照镜子,是轴对称;③钟表分针的运动,是旋转;④行驶中汽车车轮的运动,是旋转.故平移现象有1个.故选A.
点睛:本题考查了图形的平移,图形的平移只改变图形的位置,而不改变图形的形状和大小,学生易混淆图形的平移与旋转或翻转而误选.
2.D
【解析】由题意知,BE=6,DE=AB=10,
∴OE=DE-DO=10-4=6,
∴S四边形ODFC=S梯形ABEO= (AB+OE)·BE=×(10+6)×6=48.
故选D.
3.B
【解析】试题解析:∵△ABC沿AB方向平移至△DEF,平移的距离是AD,
∴AD=AB DB=5 2=3,
∴CF=AD=3.
故选B.
4.D
【解析】试题解析:平移,是指在平面内,将一个图形上的所有点都按照某个直线方向做相同距离的移动,这样的图形运动叫做图形的平移运动,简称平移.平移不改变图形的形状和大小. 平移后的图形与原图形上对应点连接的线段平行(或在同一条直线上)且相等.
故选D.
5.C
【解析】试题解析:由方程可知,在5×5方格纸中将图①中的图形N平移后的位置如图②所示,那么下面平移中正确的是:先向下移动2格,再向左移动1格;
故选C.
6.D
【解析】分析:根据平移的性质:不改变图形的形状和大小,不可旋转与翻转,将题中所示的图案通过平移后可以得到的图案是D.
详解:观察图形可知,图案D可以看作由“基本图案”经过平移得到.
故选D.
点睛:本题主要考查了图形的平移,图形的平移只改变图形的位置,而不改变图形的形状和大小,学生易混淆图形的平移与旋转或翻转,而导致错选.
7.C
【解析】∵△DEF是由△ABC通过平移得到,
∴BE=CF,
∴BE= EMBED Equation.DSMT4 (BF-EC),
∵BF=14,EC=6,
∴BE=(14-6)=4.
故选:C.
8.C
【解析】由平移的性质可知,甲、乙两只蚂蚁的行走的路程相同,且两只蚂蚁的速度相同,所以两只蚂蚁同时到达,故选C.
9.B
【解析】草地面积=长方形面积-小路面积=12×6-2×6=60(m2),
故选B.
10.(2)(4)
【解析】试题分析:(1)电风扇的转动是旋转,不属于平移;
(2)打气筒打气时,活塞的运动属于平移;
(3)钟摆的摆动是旋转,不属于平移;
(4)传送带上瓶装饮料的移动符合平移的性质,属于平移.
故选D.
点睛:本题考查图形的平移变换.图形的平移只改变图形的位置,而不改变图形的形状和大小,学生易混淆图形的平移与旋转或翻转,以致选错.
11.6;下;3.
【解析】试题解析:选取A点观察,通过图形信息知将A点向右平移6个单位,再向下平移3个单位可到D点位置,即B点到E点,C点到F点都是同样的平移方法,
△DEF是由△ABC先向右平移6格,再向下平移3格而得到的.
故答案为:6;下;3.
12.6
【解析】阴影部分为长方形,根据平移的性质可得阴影部分是长为3,宽为2,让长乘宽即为阴影部分的面积.
解:易知,当正方形ABCD向上平移2cm。则阴影长方形的宽=4-2=2cm
向右平移1cm则阴影长方形的长=4-1=3cm
所以阴影部分面积=2×3=6cm
“点睛”本题难度较低,主要考查学生对平移知识点的掌握。要注意数形结合思想的培养,运用到考试中去。
13.160
【解析】解:由图可知:矩形ABCD中去掉小路后,草坪正好可以拼成一个新的矩形,且它的长为:(18﹣2)米,宽为(11﹣1)米.所以草坪的面积应该是长×宽=(18﹣2)(11﹣1)=160(米2).故答案为:160.
点睛:本题考查了生活中的平移,根据图形得出草坪正好可以拼成一个长方形是解题的关键.
14.12.
【解析】根据平移性质,判定△A′B′C为等边三角形,然后求解.
解:由题意,得BB′=2,
∴B′C=BC-BB′=4.
由平移性质,可知A′B′=AB=4,∠A′B′C=∠ABC=60°,
∴A′B′=B′C,且∠A′B′C=60°,
∴△A′B′C为等边三角形,
∴△A′B′C的周长=3A′B′=12.
故答案为:12.
“点睛”本题考查的是平移的性质,熟知图形平移后新图形与原图形的形状和大小完全相同是解答此题的关键.
15.6+5n
【解析】每次平移5个单位,n次平移5n个单位,即BN的长为5n,加上AB的长即为ABn的长.
ABn=5n+AB=5n+6.
16.270
【解析】试题解析:由平移的性质,梯形ABCD的面积=梯形EFGH的面积,CD=HG=30cm,
∴阴影部分的面积=梯形DHGO的面积,
∵CO=6cm,
∴DO=CD-CO=30-6=24cm,
∴阴影部分的面积=(DO+HG) OG=(24+30)×10=270cm2.
故答案为:270.
17.36cm2
【解析】试题分析:根据题意得出AD=CF=2BC,EF=BC,则CE=BC,根据面积计算法则得出四边形的面积为△ABC面积的3倍,得出答案.
试题解析:根据题意可得:AD=CF=2BC,EF=BC,则CE=BC
∴四边形的面积=(CE+AD)h×=(BC+2BC)h×=.
18.(1)作图见解析;(2)4.
【解析】试题分析:(1)根据图形平移的性质画出△DEF即可;
(2)利用矩形的面积减去三个顶点上三角形的面积即可.
试题解析:(1)作图如下:
(2)由图可知,S△DEF=3×4﹣ EMBED Equation.DSMT4 ×2×4﹣×2×3﹣×2×1
=12﹣4﹣3﹣1
=4.
19.(1)mn+2nh;(2)19200cm2.
【解析】试题分析:(1)根据平移计算出地毯总长为(m+2h),然后再根据长×宽可得面积;
(2)把已知数据代入(1)中求出答案.
试题解析:
解:(1)地毯的面积为:(m+2h)·n=mn+2nh;
(2)地毯总长:80×2+160=320(cm),
320×60=19200(cm2),
答:地毯的面积为19200cm2.
点睛:此题主要考查了生活中的平移现象、代数式求值,关键是根据平移得出地毯的总长为(m+2h).
20.1421m2
【解析】试题分析:将横向的小路平移至长方形的上边,将纵向小路平移至长方形的左边,则剩余部分即为种植花草的面积.
解:将横向的小路平移至长方形的上边,将纵向小路平移至长方形的左边,如图所示:
所以种植花草的面积=(50-1)(30-1)=1421m2.
点睛:本题考查了平移在实际中的应用,将两条小路平移至长方形的边上,使种植花草的面积等于一个长方形的面积是解决此题的关键.
21. (1) 9厘米;(2) 140°;(3) AB=FD、AC=FE、BC=DE、BD=CE;(4) AB∥FD、AC∥FE.
【解析】试题分析:(1)根据平移的性质可得CE=3cm,然后根据BE=BC+CE即可得出结论;
(2)根据平移的性质得出∠FDE的度数,然后根据邻补角互补即可得出答案;
(3)直接根据平移的性质即可得出结论;
(4)根据平移的性质即可得出结论.
试题解析:
解:(1)∵△ABC沿直线l向右移了3厘米,∴CE=BD=3cm,∴BE=BC+CE=6+3=9厘米;
(2)∵∠FDE=∠B=40°,∴∠FDB=140°;
(3)相等的线段有:AB=FD、AC=FE、BC=DE、BD=CE;
(4)平行的线段有:AB∥FD、AC∥FE.
点睛:本题考查了平移的性质:平移前后的两个图形的对应线段平行且相等;对应角相等;对应点连线平行且相等.
22.答案见解析
【解析】试题分析:(1)①过点P作 垂足为即可;
②利用直尺作PE∥AB即可;
(2)根据图形平移的性质画出平移后的即可.
试题解析: ①如图1所示;
②如图1所示;
如图2所示.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
