20.1 数据的频数分布(2)同步练习
文档属性
| 名称 | 20.1 数据的频数分布(2)同步练习 |

|
|
| 格式 | doc | ||
| 文件大小 | 621.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-09 00:00:00 | ||
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
20.1数据的频数分布(2)同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
分析一组数据的分布情况,可按下列步骤整理:
(1)求 最大数与最小数的差.
(2)决定组数和组距组数=最大数-最小数组距 .
(3)决定分点:为保证每个数据都分在各组内,一般地把表示分点的数比原数据多取一位小数.
(4)列频数分布表.
(5)画频数分布直方图 .
基础知识和能力拓展精练
一、选择题
1.一个容量为60的样本中数据的最大值是187,最小值是140,取组距为6,则可以分成( )
A.7组 B.7组 C.8组 D.10组
2.已知一个样本容量为50,在频数分布直方图中,各小长方形的高比为2:3:4:1,那么第四组的频数是( )
A. 5 B. 6 C. 7 D. 8
3.为了了解本校八年级学生的体能情况,随机抽查了其中30名学生,测试了1分钟仰卧起坐次数,并给制成如图所示的频数分布直方图,请根据图中信息,计算仰卧起坐次数在25~30次的频率是( )
A. 0.4 B. 0.3 C. 0.2 D. 0.1
4.为了解某校学生今年五一期间参加社团活动时间的情况,随机抽查了其中100名学生进行统计,并绘制成如图所示的频数直方图,由图可知,参加社团活动时间在8~10小时之间的学生数是( )
A. 28 B. 24 C. 30 D. 26
5.如图是若干只电灯泡的使用寿命进行检测的频数分布折线图,由图可知检测的频数为( )
A. 20 B. 14 C. 12 D. 10
6.在样本频数分布直方图中,有11个小长方形.若中间的小长方形的面积等于其他10个小长方形面积之和的,且样本容量为160个,则中间的一组的频数为( ).
A. 0.2 B. 32 C. 0.25 D. 40
7.2000辆汽车通过某一段公路时的时速的频率分布直方图如下图所示,时速大于等于50且小于60的汽车大约有( )
A. 30辆 B. 60辆 C. 300辆 D. 600辆
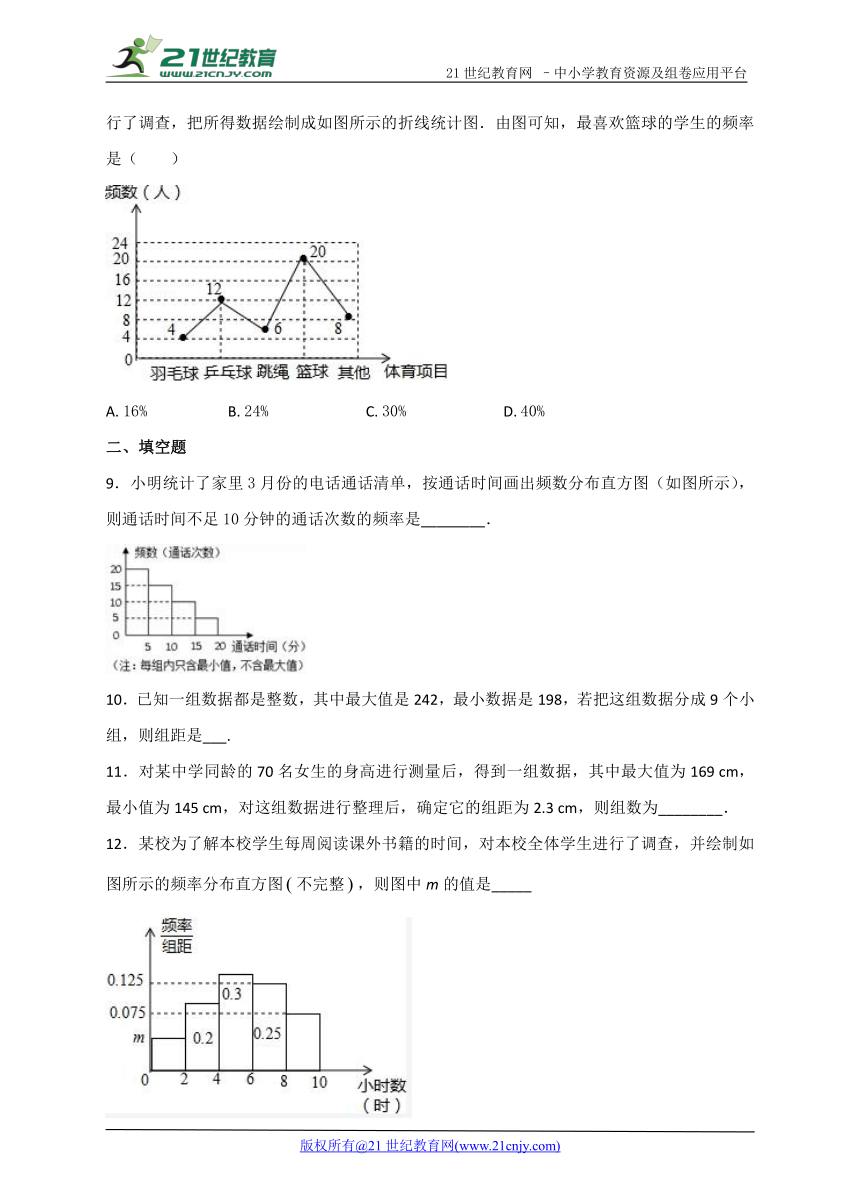
8.体育老师对八年级(2)班学生“你最喜欢的体育项目是什么?(只写一项)”的问题进行了调查,把所得数据绘制成如图所示的折线统计图.由图可知,最喜欢篮球的学生的频率是( )
A. 16% B. 24% C. 30% D. 40%
二、填空题
9.小明统计了家里3月份的电话通话清单,按通话时间画出频数分布直方图(如图所示),则通话时间不足10分钟的通话次数的频率是________.
10.已知一组数据都是整数,其中最大值是242,最小数据是198,若把这组数据分成9个小组,则组距是___.
11.对某中学同龄的70名女生的身高进行测量后,得到一组数据,其中最大值为169 cm,最小值为145 cm,对这组数据进行整理后,确定它的组距为2.3 cm,则组数为________.
12.某校为了解本校学生每周阅读课外书籍的时间,对本校全体学生进行了调查,并绘制如图所示的频率分布直方图 EMBED Equation.DSMT4 不完整,则图中m的值是_____
13.超市为了制定某个时间段收银台开放方案,统计了这个时间段本超市顾客在收银台排队付款的等待时间,并绘制成频数分布直方图(图中等待时间分钟表示大于或等于分钟而小于分钟,其余类似),这个时间段内顾客等待时间低于分钟的有__________人.
14.七年级一班共有48名学生,他们身高的频数分布直方图如图,各小长方形的高的比为1∶1∶3∶2∶1,则身高范围在__________________的学生最多,是____人.
15.如图,一项统计数据的频数分布直方图中,如果直方图关于第三组的小长方形呈轴对称图形(坐标轴忽略不计),那么,落在110~130这一组中的频数是_______
三、解答题
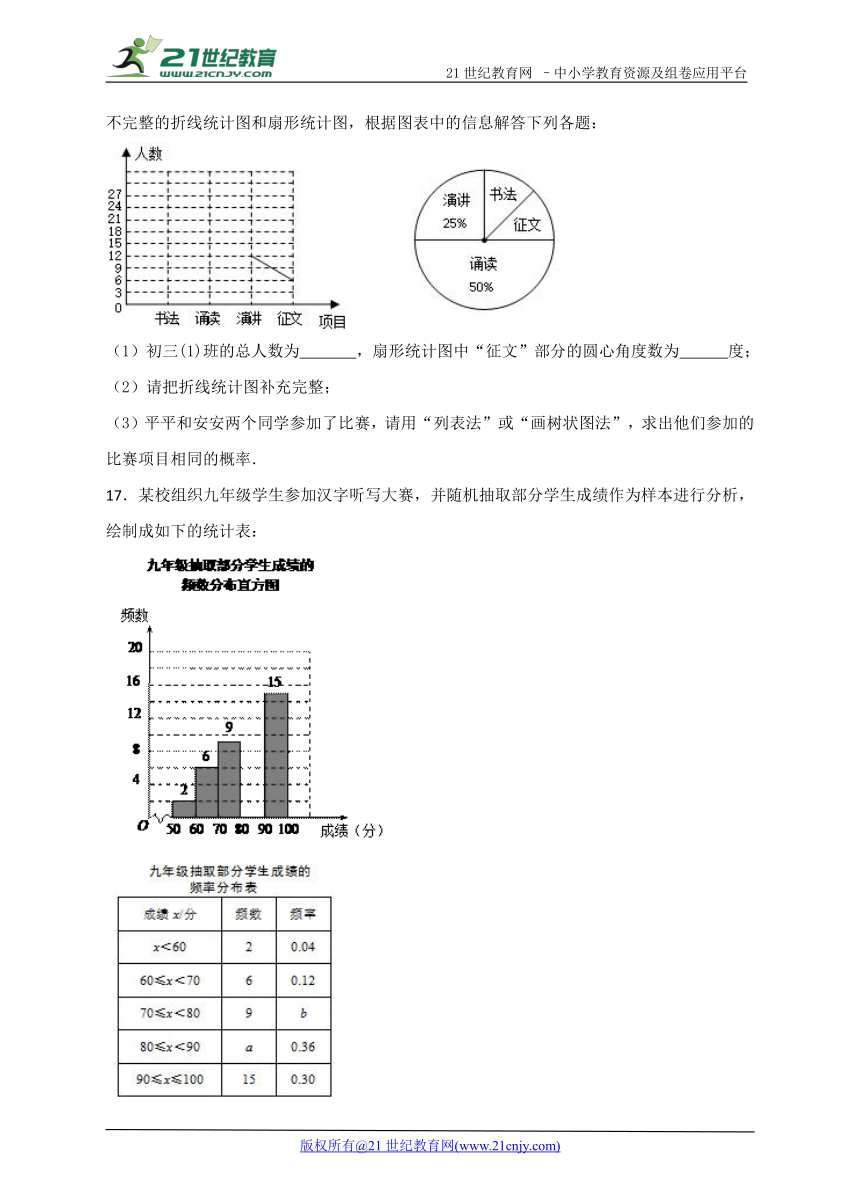
16.某中学团委会开展书法、诵读、演讲、征文四个项目(每人只参加一个项目)的比赛,初三(1)班全体同学都参加了比赛,为了解比赛的具体情况,小明收集整理数据后,绘制了以下不完整的折线统计图和扇形统计图,根据图表中的信息解答下列各题:
(1)初三(1)班的总人数为 ,扇形统计图中“征文”部分的圆心角度数为 度;
(2)请把折线统计图补充完整;
(3)平平和安安两个同学参加了比赛,请用“列表法”或“画树状图法”,求出他们参加的比赛项目相同的概率.
17.某校组织九年级学生参加汉字听写大赛,并随机抽取部分学生成绩作为样本进行分析,绘制成如下的统计表:
请根据所给信息,解答下列问题:
(1)a=_________,b=________;
(2)请补全频数分布直方图;
(3)已知该年级有400名学生参加这次比赛,若成绩在90分以上(含90分)的为优,
估计该年级成绩为优的有多少人?
18.为了加强学生的安全意识,某校组织了学生参加安全知识竞赛.从中抽取了部分学生成绩(得分数取正整数,满分为100分)进行统计,已知A组的频数a比B组的频数b小24,绘制统计频数分布直方图(未完成)和扇形图如下,请解答下列问题:
(1)样本容量为:______,a为______;
(2)n为________,E组所占比例为________;
(3)补全频数分布直方图;
(4)若成绩在80分以上记作优秀,全校共有2000名学生,估计成绩优秀学生有_________名.
19.近期,中宣部、国家发改委发出开展节俭养德全民节约行动的通知,在全社会营造厉行节约、拒绝浪费的浓厚氛围,我市某中学为了解该校学生家庭月均用电量情况,给学生布置了收集自己家中月均用电量数据的课外作业,学校随机抽取了1000名学生家庭月均用电量的数据,并将调查数据整理如下:
月均用电量a/度 频数/户 频率
0≤a<50 120 0.12
50≤a<100 240 n
100≤a<150 300 0.30
150≤a<200 m 0.16
200≤a<250 120 0.12
250≤a<300 60 0.06
合 计 1000 1
(1)频数分布表中的m=_____,n=_____;
(2)补全频数分布直方图;
(3)被调查的1000名学生家庭月均用电量的众数落在哪一个范围?
(4)求月均用电量小于150度的家庭数占被调查家庭总数的百分比.
20.“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表.
组别 成绩x分 频数(人数)
第1组 50≤x<60 6
第2组 60≤x<70 8
第3组 70≤x<80 14
第4组 80≤x<90 a
第5组 90≤x<100 10
请结合图表完成下列各题:
(1)① 表中a的值为 ;
② 把频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
21.如图是若干名同学在引体向上训练时一次测试成绩(个)的频数分布折线图.
(1)参加这次测试共有多少名同学?
(2)组中点为9个一组的频数是多少?
(3)分布两端虚设的频数为零的是哪两组?
参考答案
1.C
【解析】最大值与最小值的差为187-140=47,即最多有47个不同数据,分组为47÷6=7,因此取整可知可分成8组.
故选:C.
2.A
【解析】解:∵频数分布直方图中各个长方形的高之比依次为2:3:4:1,样本容量为50,∴第四小组的频数为50× EMBED Equation.DSMT4 =5.故选A.
点睛:本题考查了频数(率)分布直方图,要知道,频数分布直方图中各个长方形的高之比即为各组频数之比.
3.A
【解析】解:由图可知:仰卧起坐次数在25~30次的频率= EMBED Equation.DSMT4 =0.4.故选A.
4.A
【解析】试题解析:由图可知,参加社团活动时间在8~10小时之间的学生数是:
故选A.
5.A
【解析】解:由图可知:检测的频数为(2+4+8+6)=20;故选A.
6.B
【解析】根据频率分布直方图的意义,小矩形的面积之和为1,可设中间长方形的面积为x,则其他的10个小长方形的面积为4x,所以可得x+4x=1,解得x=0.2;又因为样本容量为160,所以可求得中间一组的频数为160×0.2=32.
故选:B.
7.D
【解析】根据频数分布直方图的特点,可知该组的=0.03,又由于组距为10,所以该组的频率为0.3,因此该组的频数=0.3×2000=600.
故选:D.
点睛:此题主要考查了频数分布直方图的特点,关键是根据频数分布直方图求出这组的频率,再根据频率=频数÷总数.
8.D
【解析】解:读图可知:共有(4+12+6+20+8)=50人,其中最喜欢篮球的有20人,故频率最喜欢篮球的频率=20÷50=0.4.故选D.
9.0.7
【解析】由图可知:小明家3月份通话总次数为20+15+10+5=50(次);其中通话不足10分钟的次数为20+15=35(次),
∴通话时间不足10分钟的通话次数的频率是35÷50=0.7.
故答案为:0.7.
10.5;
【解析】试题解析:在样本数据中最大值与最小值的差为44,
若把这组数据分成9个小组,那么由于 则组距是5.
故答案为:5.
11.11
【解析】根据组距的确定方法,可知最大值-最小值=169-145=24,又因为组距2.3,所以24÷2.3≈11(组).
故答案为:11.
12.0.05
【解析】试题分析:由题意可得组距为2,
则8-10小时对应的频率为:0.075×2=0.15,
所以0-2小时对应的频率为:1-0.2-0.3-0.25-0.15=0.1,
所以m=0.1 ÷2=0.05
故答案是:0.05.
点睛:本题考查了频率分布直方图,了解各组的频率的和是1是关键.
13.60
【解析】根据频数分布直方图得到前3组的等待时间不少于3分钟,而它们的频数分别为10,35,15,
所以这个时间段内顾客等待时间低于3分钟的人数为(人).
故答案为60.
14. 165cm~170cm 18
【解析】试题解析:八年级一班共有48名学生,他们身高的频数分布直方图如图,各小长方形的高的比为1:1:3:2:1,
∴最高的即表示在这个身高范围内的学生最多,
∴165cm 170cm这个身高范围内的学生最多,
这个身高范围内的学生有:人.
故答案为:165cm 170cm,18.
15.300
【解析】解:如果直方图关于第三组的小长方形呈轴对称图形,则110~130这一组与第二组频数应相等,故其频数为300.
点睛:解本题要懂得频率分布直分图的意义,了解频率分布直分图是一种以频数为纵向指标的条形统计图.
16.(1)48, 45;(2)作图见解析;(3)
【解析】(1)由演讲人数12人,占25%,即可求得九(2)全班人数;
(2)首先求得书法与国学诵读人数,继而补全折线统计图;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与他们参加的比赛项目相同的情况,再利用概率公式求解即可求得答案.
解:(1)∵演讲人数12人,占25%,
∴九(2)全班人数为:12+25%=48(人);
45;
(2)所画折线统计图如下图所示;
(3)分别用A、B、C、D表示书法、诵读、演讲、征文,所画树状图如下:
∵共有16种等可能的结果,他们参加的比赛项目相同的有4种情况,
∴他们参加的比赛项目相同的概率为: .
“点睛”此题考查了列表法或树状图法求概率以及折线与扇形统计图的知识. 注意掌握折线统计图与扇形统计图的对应关系.
17. 18 0.18
【解析】分析:(1)直接利用频数÷总数=频率,进而得出答案;(2)直接利用(1)中所求,补全条形统计图即可;(3)直接利用样本估计总体进而得出答案.
详解:(1)抽取的总人数是2÷0.04=50(人)a=50×0.36=18,
b=9÷50=0.18;
(2)频数分布直方图见;
(3)400×0.30=120.
点睛:本题考查了读频数分布直方图的能力和利用统计图获取信息的能力,利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
18. 200 16 126 12% 940
【解析】分析:(1)由于A组的频数比B组小24,而A组的频率比B组小12%,则可计算出调查的总人数,然后计算a和b的值;
(2)用360度乘以D组的频率可得到n的值,根据百分比之和为1可得E组百分比;
(3)计算出C和E组的频数后补全频数分布直方图;
(4)利用样本估计总体,用2000乘以D组和E组的频率和即可.
详解:(1)样本容量为24÷(20%﹣8%)=200,a=200×8%=16.故答案为:200,16;
(2)n=360×=126,E组所占百分比为1﹣(8%+20%+25%+×100%)=12%.故答案为:126,12;
(3)C组的频数为200×25%=50,E组的频数为200﹣16﹣40﹣50﹣70=24,补全频数分布直方图为:
(4)2000×=940,所以估计成绩优秀的学生有940人.故答案为:940.
点睛:本题考查了频数(率)分布直方图:提高读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.也考查了用样本估计总体.
19. 160 0.24
【解析】试题分析:(1)根据抽查的总户数和频率=,即可求出答案;
(2)根据图表所给的数据直接补全频数分布直方图;
(3)根据众数的定义和统计表所给的数据即可求出答案;
(4)把每月均用电量小于150度的家庭数加起来,再除以总户数,即可求出答案.
试题解析:解:(1)m=1000×0.16=160,n=240÷1000=0.24.故答案为:160、0.24;
(2)补全条形图如下:
(3)被调查的1000名学生家庭月均用电量的众数落在100≤a<150;
(4)月均用电量小于150度的家庭数占被调查家庭总数的百分比为×100%=66%.
点睛:本题考查了读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
20.(1)12;(2)详见解析;(3)44%.
【解析】试题分析:
(1)由参加决赛的学生总数50减去频数分布表中的已知频数即可得到a的值;
(2)根据(1)中求得的a的值将频数分布直方图规范的补充完整即可;
(3)结合(1)中求得的a的值和频数分布表中的已知数据计算出不低于80分的学生人数,由这个人数÷50×100%即可得到优秀率.
试题解析;
(1)由题意可得:a=50-6-8-14-10=12;
(2)频数分布直方图补充完整如下图所示:
(3)由题意可得,这次比赛的优秀率为: .
答:这次测试的优秀率为44%.
21.(1)23;(2)10;(3) 4.5~5.5,10.5~11.5.
【解析】试题分析:(1)根据图中的信息,找到符合条件的数据,再进一步计算.
(2)观察即可得出组中点为9个一组的频数,再除以总数即可求得频率.
(3)仔细观察,即可得出正确答案.
试题解析:
(1)2+4+5+10+2=23名;
(2)组中点为9个一组的频数是10;
(3)分布两端虚设的频数为零的两组是4.5~5.5和10.5~11.5.
点睛:本题考查读频数分布折线图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
20.1数据的频数分布(2)同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
分析一组数据的分布情况,可按下列步骤整理:
(1)求 最大数与最小数的差.
(2)决定组数和组距组数=最大数-最小数组距 .
(3)决定分点:为保证每个数据都分在各组内,一般地把表示分点的数比原数据多取一位小数.
(4)列频数分布表.
(5)画频数分布直方图 .
基础知识和能力拓展精练
一、选择题
1.一个容量为60的样本中数据的最大值是187,最小值是140,取组距为6,则可以分成( )
A.7组 B.7组 C.8组 D.10组
2.已知一个样本容量为50,在频数分布直方图中,各小长方形的高比为2:3:4:1,那么第四组的频数是( )
A. 5 B. 6 C. 7 D. 8
3.为了了解本校八年级学生的体能情况,随机抽查了其中30名学生,测试了1分钟仰卧起坐次数,并给制成如图所示的频数分布直方图,请根据图中信息,计算仰卧起坐次数在25~30次的频率是( )
A. 0.4 B. 0.3 C. 0.2 D. 0.1
4.为了解某校学生今年五一期间参加社团活动时间的情况,随机抽查了其中100名学生进行统计,并绘制成如图所示的频数直方图,由图可知,参加社团活动时间在8~10小时之间的学生数是( )
A. 28 B. 24 C. 30 D. 26
5.如图是若干只电灯泡的使用寿命进行检测的频数分布折线图,由图可知检测的频数为( )
A. 20 B. 14 C. 12 D. 10
6.在样本频数分布直方图中,有11个小长方形.若中间的小长方形的面积等于其他10个小长方形面积之和的,且样本容量为160个,则中间的一组的频数为( ).
A. 0.2 B. 32 C. 0.25 D. 40
7.2000辆汽车通过某一段公路时的时速的频率分布直方图如下图所示,时速大于等于50且小于60的汽车大约有( )
A. 30辆 B. 60辆 C. 300辆 D. 600辆
8.体育老师对八年级(2)班学生“你最喜欢的体育项目是什么?(只写一项)”的问题进行了调查,把所得数据绘制成如图所示的折线统计图.由图可知,最喜欢篮球的学生的频率是( )
A. 16% B. 24% C. 30% D. 40%
二、填空题
9.小明统计了家里3月份的电话通话清单,按通话时间画出频数分布直方图(如图所示),则通话时间不足10分钟的通话次数的频率是________.
10.已知一组数据都是整数,其中最大值是242,最小数据是198,若把这组数据分成9个小组,则组距是___.
11.对某中学同龄的70名女生的身高进行测量后,得到一组数据,其中最大值为169 cm,最小值为145 cm,对这组数据进行整理后,确定它的组距为2.3 cm,则组数为________.
12.某校为了解本校学生每周阅读课外书籍的时间,对本校全体学生进行了调查,并绘制如图所示的频率分布直方图 EMBED Equation.DSMT4 不完整,则图中m的值是_____
13.超市为了制定某个时间段收银台开放方案,统计了这个时间段本超市顾客在收银台排队付款的等待时间,并绘制成频数分布直方图(图中等待时间分钟表示大于或等于分钟而小于分钟,其余类似),这个时间段内顾客等待时间低于分钟的有__________人.
14.七年级一班共有48名学生,他们身高的频数分布直方图如图,各小长方形的高的比为1∶1∶3∶2∶1,则身高范围在__________________的学生最多,是____人.
15.如图,一项统计数据的频数分布直方图中,如果直方图关于第三组的小长方形呈轴对称图形(坐标轴忽略不计),那么,落在110~130这一组中的频数是_______
三、解答题
16.某中学团委会开展书法、诵读、演讲、征文四个项目(每人只参加一个项目)的比赛,初三(1)班全体同学都参加了比赛,为了解比赛的具体情况,小明收集整理数据后,绘制了以下不完整的折线统计图和扇形统计图,根据图表中的信息解答下列各题:
(1)初三(1)班的总人数为 ,扇形统计图中“征文”部分的圆心角度数为 度;
(2)请把折线统计图补充完整;
(3)平平和安安两个同学参加了比赛,请用“列表法”或“画树状图法”,求出他们参加的比赛项目相同的概率.
17.某校组织九年级学生参加汉字听写大赛,并随机抽取部分学生成绩作为样本进行分析,绘制成如下的统计表:
请根据所给信息,解答下列问题:
(1)a=_________,b=________;
(2)请补全频数分布直方图;
(3)已知该年级有400名学生参加这次比赛,若成绩在90分以上(含90分)的为优,
估计该年级成绩为优的有多少人?
18.为了加强学生的安全意识,某校组织了学生参加安全知识竞赛.从中抽取了部分学生成绩(得分数取正整数,满分为100分)进行统计,已知A组的频数a比B组的频数b小24,绘制统计频数分布直方图(未完成)和扇形图如下,请解答下列问题:
(1)样本容量为:______,a为______;
(2)n为________,E组所占比例为________;
(3)补全频数分布直方图;
(4)若成绩在80分以上记作优秀,全校共有2000名学生,估计成绩优秀学生有_________名.
19.近期,中宣部、国家发改委发出开展节俭养德全民节约行动的通知,在全社会营造厉行节约、拒绝浪费的浓厚氛围,我市某中学为了解该校学生家庭月均用电量情况,给学生布置了收集自己家中月均用电量数据的课外作业,学校随机抽取了1000名学生家庭月均用电量的数据,并将调查数据整理如下:
月均用电量a/度 频数/户 频率
0≤a<50 120 0.12
50≤a<100 240 n
100≤a<150 300 0.30
150≤a<200 m 0.16
200≤a<250 120 0.12
250≤a<300 60 0.06
合 计 1000 1
(1)频数分布表中的m=_____,n=_____;
(2)补全频数分布直方图;
(3)被调查的1000名学生家庭月均用电量的众数落在哪一个范围?
(4)求月均用电量小于150度的家庭数占被调查家庭总数的百分比.
20.“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表.
组别 成绩x分 频数(人数)
第1组 50≤x<60 6
第2组 60≤x<70 8
第3组 70≤x<80 14
第4组 80≤x<90 a
第5组 90≤x<100 10
请结合图表完成下列各题:
(1)① 表中a的值为 ;
② 把频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
21.如图是若干名同学在引体向上训练时一次测试成绩(个)的频数分布折线图.
(1)参加这次测试共有多少名同学?
(2)组中点为9个一组的频数是多少?
(3)分布两端虚设的频数为零的是哪两组?
参考答案
1.C
【解析】最大值与最小值的差为187-140=47,即最多有47个不同数据,分组为47÷6=7,因此取整可知可分成8组.
故选:C.
2.A
【解析】解:∵频数分布直方图中各个长方形的高之比依次为2:3:4:1,样本容量为50,∴第四小组的频数为50× EMBED Equation.DSMT4 =5.故选A.
点睛:本题考查了频数(率)分布直方图,要知道,频数分布直方图中各个长方形的高之比即为各组频数之比.
3.A
【解析】解:由图可知:仰卧起坐次数在25~30次的频率= EMBED Equation.DSMT4 =0.4.故选A.
4.A
【解析】试题解析:由图可知,参加社团活动时间在8~10小时之间的学生数是:
故选A.
5.A
【解析】解:由图可知:检测的频数为(2+4+8+6)=20;故选A.
6.B
【解析】根据频率分布直方图的意义,小矩形的面积之和为1,可设中间长方形的面积为x,则其他的10个小长方形的面积为4x,所以可得x+4x=1,解得x=0.2;又因为样本容量为160,所以可求得中间一组的频数为160×0.2=32.
故选:B.
7.D
【解析】根据频数分布直方图的特点,可知该组的=0.03,又由于组距为10,所以该组的频率为0.3,因此该组的频数=0.3×2000=600.
故选:D.
点睛:此题主要考查了频数分布直方图的特点,关键是根据频数分布直方图求出这组的频率,再根据频率=频数÷总数.
8.D
【解析】解:读图可知:共有(4+12+6+20+8)=50人,其中最喜欢篮球的有20人,故频率最喜欢篮球的频率=20÷50=0.4.故选D.
9.0.7
【解析】由图可知:小明家3月份通话总次数为20+15+10+5=50(次);其中通话不足10分钟的次数为20+15=35(次),
∴通话时间不足10分钟的通话次数的频率是35÷50=0.7.
故答案为:0.7.
10.5;
【解析】试题解析:在样本数据中最大值与最小值的差为44,
若把这组数据分成9个小组,那么由于 则组距是5.
故答案为:5.
11.11
【解析】根据组距的确定方法,可知最大值-最小值=169-145=24,又因为组距2.3,所以24÷2.3≈11(组).
故答案为:11.
12.0.05
【解析】试题分析:由题意可得组距为2,
则8-10小时对应的频率为:0.075×2=0.15,
所以0-2小时对应的频率为:1-0.2-0.3-0.25-0.15=0.1,
所以m=0.1 ÷2=0.05
故答案是:0.05.
点睛:本题考查了频率分布直方图,了解各组的频率的和是1是关键.
13.60
【解析】根据频数分布直方图得到前3组的等待时间不少于3分钟,而它们的频数分别为10,35,15,
所以这个时间段内顾客等待时间低于3分钟的人数为(人).
故答案为60.
14. 165cm~170cm 18
【解析】试题解析:八年级一班共有48名学生,他们身高的频数分布直方图如图,各小长方形的高的比为1:1:3:2:1,
∴最高的即表示在这个身高范围内的学生最多,
∴165cm 170cm这个身高范围内的学生最多,
这个身高范围内的学生有:人.
故答案为:165cm 170cm,18.
15.300
【解析】解:如果直方图关于第三组的小长方形呈轴对称图形,则110~130这一组与第二组频数应相等,故其频数为300.
点睛:解本题要懂得频率分布直分图的意义,了解频率分布直分图是一种以频数为纵向指标的条形统计图.
16.(1)48, 45;(2)作图见解析;(3)
【解析】(1)由演讲人数12人,占25%,即可求得九(2)全班人数;
(2)首先求得书法与国学诵读人数,继而补全折线统计图;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与他们参加的比赛项目相同的情况,再利用概率公式求解即可求得答案.
解:(1)∵演讲人数12人,占25%,
∴九(2)全班人数为:12+25%=48(人);
45;
(2)所画折线统计图如下图所示;
(3)分别用A、B、C、D表示书法、诵读、演讲、征文,所画树状图如下:
∵共有16种等可能的结果,他们参加的比赛项目相同的有4种情况,
∴他们参加的比赛项目相同的概率为: .
“点睛”此题考查了列表法或树状图法求概率以及折线与扇形统计图的知识. 注意掌握折线统计图与扇形统计图的对应关系.
17. 18 0.18
【解析】分析:(1)直接利用频数÷总数=频率,进而得出答案;(2)直接利用(1)中所求,补全条形统计图即可;(3)直接利用样本估计总体进而得出答案.
详解:(1)抽取的总人数是2÷0.04=50(人)a=50×0.36=18,
b=9÷50=0.18;
(2)频数分布直方图见;
(3)400×0.30=120.
点睛:本题考查了读频数分布直方图的能力和利用统计图获取信息的能力,利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
18. 200 16 126 12% 940
【解析】分析:(1)由于A组的频数比B组小24,而A组的频率比B组小12%,则可计算出调查的总人数,然后计算a和b的值;
(2)用360度乘以D组的频率可得到n的值,根据百分比之和为1可得E组百分比;
(3)计算出C和E组的频数后补全频数分布直方图;
(4)利用样本估计总体,用2000乘以D组和E组的频率和即可.
详解:(1)样本容量为24÷(20%﹣8%)=200,a=200×8%=16.故答案为:200,16;
(2)n=360×=126,E组所占百分比为1﹣(8%+20%+25%+×100%)=12%.故答案为:126,12;
(3)C组的频数为200×25%=50,E组的频数为200﹣16﹣40﹣50﹣70=24,补全频数分布直方图为:
(4)2000×=940,所以估计成绩优秀的学生有940人.故答案为:940.
点睛:本题考查了频数(率)分布直方图:提高读频数分布直方图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.也考查了用样本估计总体.
19. 160 0.24
【解析】试题分析:(1)根据抽查的总户数和频率=,即可求出答案;
(2)根据图表所给的数据直接补全频数分布直方图;
(3)根据众数的定义和统计表所给的数据即可求出答案;
(4)把每月均用电量小于150度的家庭数加起来,再除以总户数,即可求出答案.
试题解析:解:(1)m=1000×0.16=160,n=240÷1000=0.24.故答案为:160、0.24;
(2)补全条形图如下:
(3)被调查的1000名学生家庭月均用电量的众数落在100≤a<150;
(4)月均用电量小于150度的家庭数占被调查家庭总数的百分比为×100%=66%.
点睛:本题考查了读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
20.(1)12;(2)详见解析;(3)44%.
【解析】试题分析:
(1)由参加决赛的学生总数50减去频数分布表中的已知频数即可得到a的值;
(2)根据(1)中求得的a的值将频数分布直方图规范的补充完整即可;
(3)结合(1)中求得的a的值和频数分布表中的已知数据计算出不低于80分的学生人数,由这个人数÷50×100%即可得到优秀率.
试题解析;
(1)由题意可得:a=50-6-8-14-10=12;
(2)频数分布直方图补充完整如下图所示:
(3)由题意可得,这次比赛的优秀率为: .
答:这次测试的优秀率为44%.
21.(1)23;(2)10;(3) 4.5~5.5,10.5~11.5.
【解析】试题分析:(1)根据图中的信息,找到符合条件的数据,再进一步计算.
(2)观察即可得出组中点为9个一组的频数,再除以总数即可求得频率.
(3)仔细观察,即可得出正确答案.
试题解析:
(1)2+4+5+10+2=23名;
(2)组中点为9个一组的频数是10;
(3)分布两端虚设的频数为零的两组是4.5~5.5和10.5~11.5.
点睛:本题考查读频数分布折线图的能力和利用统计图获取信息的能力.利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
