20.2.2 数据的离散程度同步练习
图片预览

文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
20.2.2 数据的离散程度同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.方差设一组数据是x1,x2,…,xn,它们的平均数是,我们用S2=[x1﹣)2+(x2﹣)2+(x3﹣)2+(x4﹣)2+(x5﹣)2])来衡量这组数据的离散程度,叫做这组数据的方差.
2.在实际问题中,常用样本方差估计总体方差,在平均数相同的情况下,方差越大,则这组数据对平均数的离散程度也越大
基础知识和能力拓展精练
一、选择题
1.有一组数据如下:2,a,3,6,5,它们的平均数是4,那么这组数据的方差是 ( )
A. 4 B. C. D. 2
2.若一组数据x1,x2,x3,x4,x5,x6的平均数是2,方差是2,则另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2,3x6﹣2的平均数和方差分别是( )
A. 2,2 B. 2,18 C. 4,6 D. 4,18
3.将一组数据中的每一个数都加上1得到一组新的数据,那么下列四个统计量中,值保持不变的是( )
A. 方差 B. 平均数 C. 中位数 D. 众数
4.一组数据:1,3,3,5,若添加一个数据3,则发生变化的统计量是( )
A. 平均数 B. 众数 C. 中位数 D. 方差
5.已知一组数据:x1,x2,x3,x4,x5,x6的平均数是2,方差是3,则另一组数据:3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2,3x6﹣2的平均数和方差分别是( )
A. 2,3 B. 2,9 C. 4,25 D. 4,27
6.某数学兴趣小组6名成员通过一次数学竞赛进行组内评比,他们的成绩分别是89,92,91,93,96,91,则关于这组数据说法正确的有( )
A. 中位数是92.5 B. 平均数是92 C. 众数是96 D. 方差是5
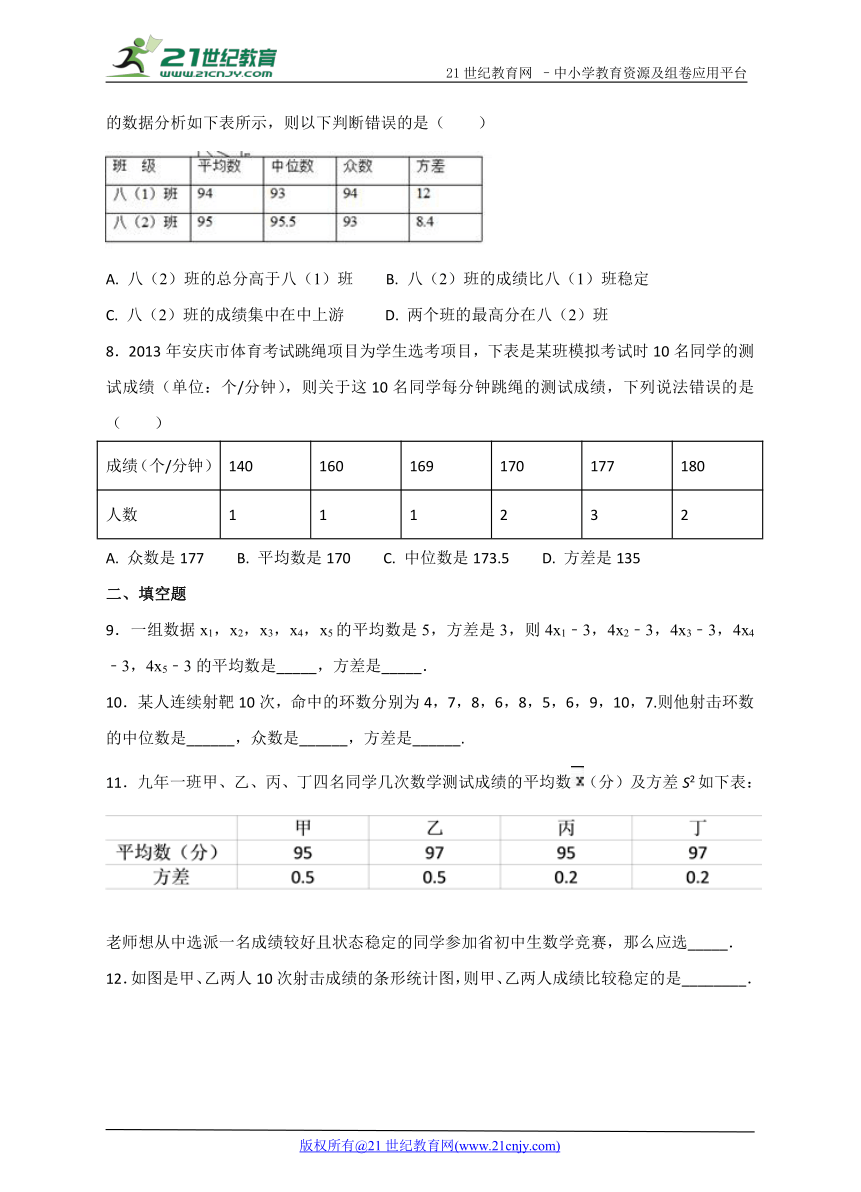
7.某校八年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛.各参赛选手成绩的数据分析如下表所示,则以下判断错误的是( )
A. 八(2)班的总分高于八(1)班 B. 八(2)班的成绩比八(1)班稳定
C. 八(2)班的成绩集中在中上游 D. 两个班的最高分在八(2)班
8.2013年安庆市体育考试跳绳项目为学生选考项目,下表是某班模拟考试时10名同学的测试成绩(单位:个/分钟),则关于这10名同学每分钟跳绳的测试成绩,下列说法错误的是( )
成绩(个/分钟) 140 160 169 170 177 180
人数 1 1 1 2 3 2
A. 众数是177 B. 平均数是170 C. 中位数是173.5 D. 方差是135
二、填空题
9.一组数据x1,x2,x3,x4,x5的平均数是5,方差是3,则4x1﹣3,4x2﹣3,4x3﹣3,4x4﹣3,4x5﹣3的平均数是_____,方差是_____.
10.某人连续射靶10次,命中的环数分别为4,7,8,6,8,5,6,9,10,7.则他射击环数的中位数是______,众数是______,方差是______.
11.九年一班甲、乙、丙、丁四名同学几次数学测试成绩的平均数(分)及方差S2如下表:
老师想从中选派一名成绩较好且状态稳定的同学参加省初中生数学竞赛,那么应选_____.
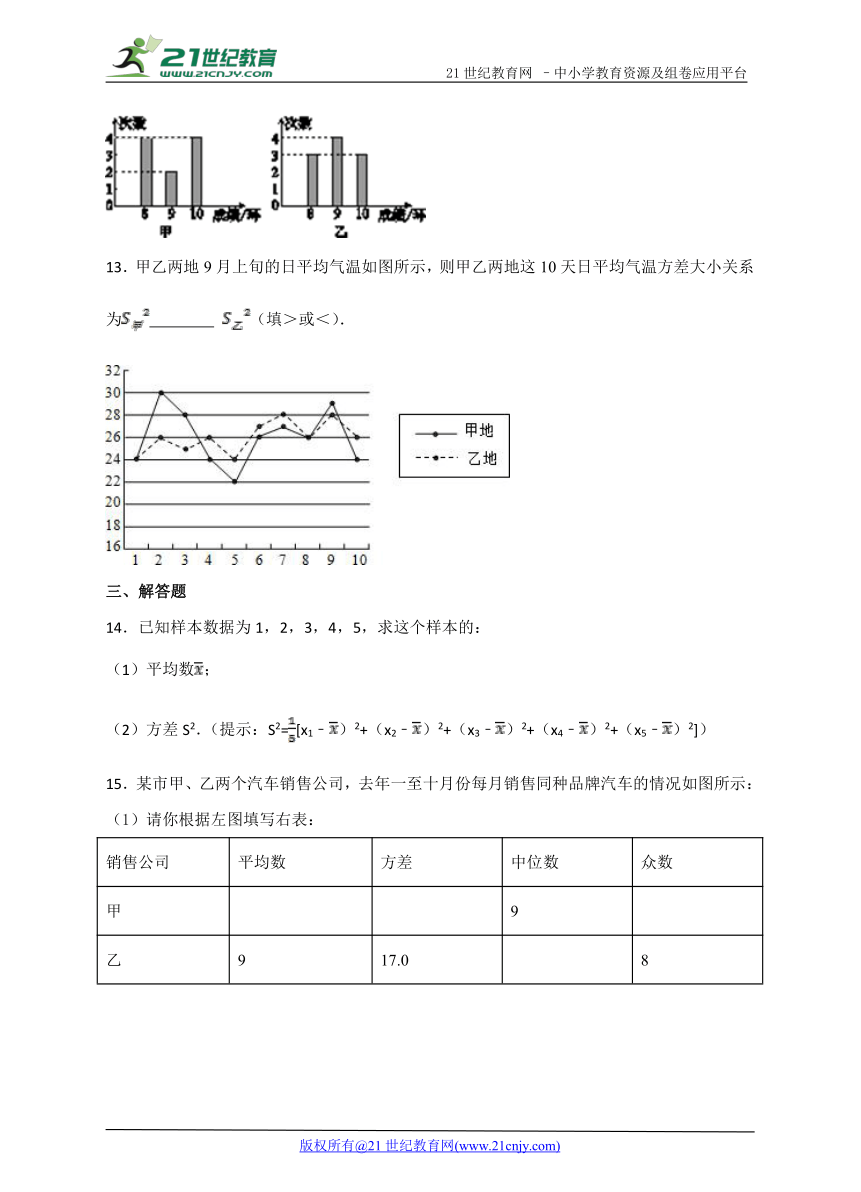
12.如图是甲、乙两人10次射击成绩的条形统计图,则甲、乙两人成绩比较稳定的是________.
13.甲乙两地9月上旬的日平均气温如图所示,则甲乙两地这10天日平均气温方差大小关系为 (填>或<).
三、解答题
14.已知样本数据为1,2,3,4,5,求这个样本的:
(1)平均数;
(2)方差S2.(提示:S2=[x1﹣)2+(x2﹣)2+(x3﹣)2+(x4﹣)2+(x5﹣)2])
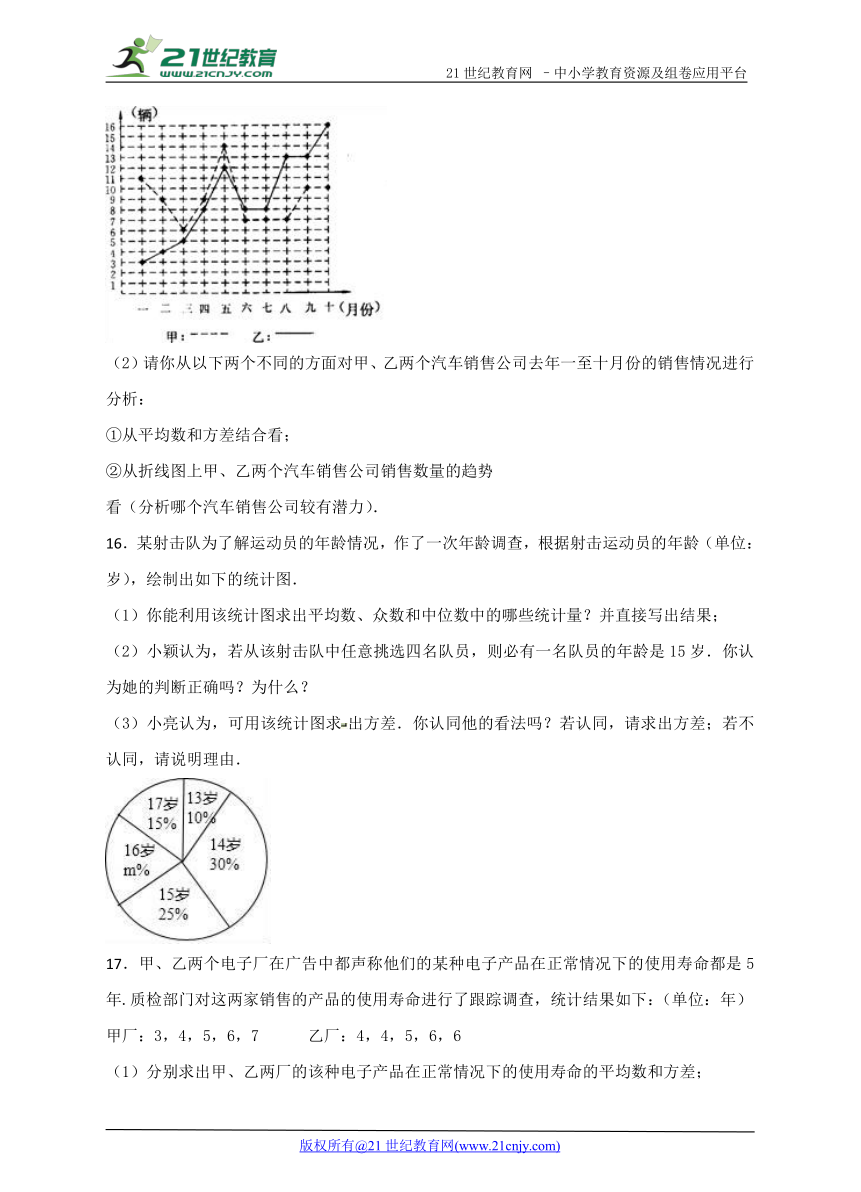
15.某市甲、乙两个汽车销售公司,去年一至十月份每月销售同种品牌汽车的情况如图所示:
(1)请你根据左图填写右表:
销售公司 平均数 方差 中位数 众数
甲 9
乙 9 17.0 8
(2)请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析:
①从平均数和方差结合看;
②从折线图上甲、乙两个汽车销售公司销售数量的趋势
看(分析哪个汽车销售公司较有潜力).
16.某射击队为了解运动员的年龄情况,作了一次年龄调查,根据射击运动员的年龄(单位:岁),绘制出如下的统计图.
(1)你能利用该统计图求出平均数、众数和中位数中的哪些统计量?并直接写出结果;
(2)小颖认为,若从该射击队中任意挑选四名队员,则必有一名队员的年龄是15岁.你认为她的判断正确吗?为什么?
(3)小亮认为,可用该统计图求出方差.你认同他的看法吗?若认同,请求出方差;若不认同,请说明理由.
17.甲、乙两个电子厂在广告中都声称他们的某种电子产品在正常情况下的使用寿命都是5年.质检部门对这两家销售的产品的使用寿命进行了跟踪调查,统计结果如下:(单位:年)
甲厂:3,4,5,6,7 乙厂:4,4,5,6,6
(1)分别求出甲、乙两厂的该种电子产品在正常情况下的使用寿命的平均数和方差;
(2)如果你是顾客,你会选购哪家电子厂的产品?说明理由.
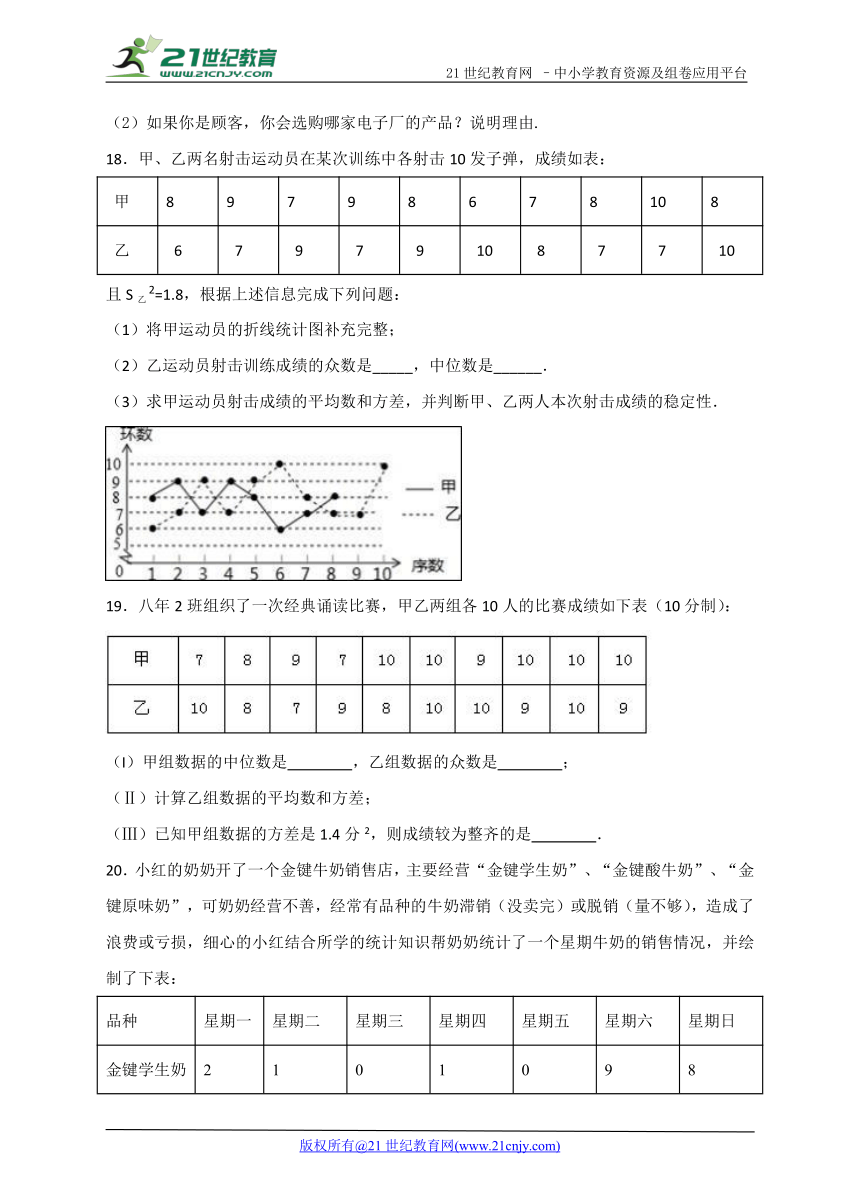
18.甲、乙两名射击运动员在某次训练中各射击10发子弹,成绩如表:
甲 8 9 7 9 8 6 7 8 10 8
乙 6 7 9 7 9 10 8 7 7 10
且S乙2=1.8,根据上述信息完成下列问题:
(1)将甲运动员的折线统计图补充完整;
(2)乙运动员射击训练成绩的众数是_____,中位数是______.
(3)求甲运动员射击成绩的平均数和方差,并判断甲、乙两人本次射击成绩的稳定性.
19.八年2班组织了一次经典诵读比赛,甲乙两组各10人的比赛成绩如下表(10 分制):
(I)甲组数据的中位数是 ,乙组数据的众数是 ;
(Ⅱ)计算乙组数据的平均数和方差;
(Ⅲ)已知甲组数据的方差是1.4分2,则成绩较为整齐的是 .
20.小红的奶奶开了一个金键牛奶销售店,主要经营“金键学生奶”、“金键酸牛奶”、“金键原味奶”,可奶奶经营不善,经常有品种的牛奶滞销(没卖完)或脱销(量不够),造成了浪费或亏损,细心的小红结合所学的统计知识帮奶奶统计了一个星期牛奶的销售情况,并绘制了下表:
品种 星期一 星期二 星期三 星期四 星期五 星期六 星期日
金键学生奶 2 1 0 1 0 9 8
金键酸牛奶 70 70 80 75 84 81 100
金键原味奶 40 30 35 30 38 47 60
(1)计算各品种牛奶的日平均销售量,并说明哪种牛奶销量最高;
(2)计算各品种牛奶的方差(保留两位小数),并比较哪种牛奶销量最稳定;
(3)假如你是小红,你会对奶奶有哪些好的建议。
参考答案
1.D
【解析】分析:先由平均数的公式计算出a的值,再根据方差的公式计算即可.
详解:∵数据2,a,3,6,5的平均数是4,∴(2+a+3+6+5)÷5=4,∴a=4,∴这组数据的方差S2= [(2﹣4)2+(4﹣4)2+(3﹣4)2+(6﹣4)2+(5﹣4)2]=2.
故选D.
点睛:本题考查了方差的定义:一般地设n个数据,x1,x2,…xn的平均数为,则方差S2= [(x1﹣)2+(x2﹣)2+…+(xn﹣)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
2.D
【解析】分析:数据的平均数比数据的平均数的3倍少2;数据的方差是数据的方差的9倍,据此求解即可.
详解:∵数据的平均数是2,
∴数据的平均数是:
∵数据的方差是2,
∴
∴数据的方差是:
,
=18.
∴另一组数据的平均数和方差分别是4,18.
故选:D.
点睛:考查平均数和方差公式,熟练记忆和运用公式是解题的关键.
3.A
【解析】分析:根据平均数和方差的特点,一组数都加上或减去同一个不等于0的常数后,方差不变,平均数改变,即可得出答案.
详解:一组数据x1,x2,…xa的每一个数都加上同一数1,则新数据x1+1,x2+1,…xn+1的平均数改变,但是方差不变.
故选A.
点睛:本题考查了方差和平均数,一般地设n个数据,x1,x2,…xn的平均数为,则方差S2=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2],掌握平均数和方差的特点是本题的关键.
4.D
【解析】解:原数据的1、3、3、5的平均数为=3,中位数为=3,众数为3,方差为×[(1﹣3)2+(3﹣3)2×2+(5﹣3)2]=2;
新数据1、3、3、3、5的平均数为=3,中位数为3,众数为3,方差为×[(1﹣3)2+(3﹣3)2×3+(5﹣3)2]=1.6;
∴添加一个数据3,方差发生变化.故选D.
5.D
【解析】解:由题知得:x1+x2+x3+x4+x5+x6=2×6=12,S12=[(x1﹣2)2+(x2﹣2)2+(x3﹣2)2+(x4﹣2)2+(x5﹣2)2+(x6﹣2)2]
=[(x12+x22+x32+x42+x52+x62)﹣4(x1+x2+x3+x4+x5+x6)+4×6]=3,∴(x12+x22+x32+x42+x52+x62)=42.
另一组数据的平均数=[3x1﹣2+3x2﹣2+3x3﹣2+3x4﹣2+3x5﹣2+3x6﹣2]=[3(x1+x2+x3+x4+x5+x6)﹣2×5]=[3×12﹣12]=×24=4,
另一组数据的方差=[(3x1﹣2﹣4)2+(3x2﹣2﹣4)2+(3x3﹣2﹣4)2+(3x4﹣2﹣4)2+(3x5﹣2﹣4)2+(3x6﹣2﹣4)2]
=[9(x12+x22+x32+x42+x52+x62)﹣36(x1+x2+x3+x4+x5+x6)+36×6]=[9×42﹣36×12+216]=×162=27.
故选D.
6.B
【解析】试题解析:这组数据按照从小到大的顺序排列为:89,91,91,92,93,96,
则中位数为: ,故A错误;
平均数为: ,故B正确;
众数为:91,故C错误;
方差S2=
=,故D错误.
故选A.
7.D
【解析】分析:根据平均数、中位数、众数和方差的性质就可以得出正确答案.
详解:根据平均分可知八(1)班的总分为940分,八(2)班的总分为950分,故A正确;八(2)班的方差小于八(1)班的方差,则八(2)班的成绩比较稳定,故B正确;根据中位数和平均分可知八(2)班的成绩集中在中上游,故C正确;最高分从这张表格上无法显示,故D错误;故本题选D.
点睛:本题主要考查的就是平均数、中位数、方差及众数的作用,属于基础题型.解决本题的关键就是要明白各数据的作用.
8.D
【解析】A、这组数据中177出现次数最多,即众数为177,此选项正确;
B、这组数据的平均数是:(140+160+169+170×2+177×3+180×2)÷10=170,此选项正确;
C、∵共有10个数,
∴中位数是第5个和6个数的平均数,
∴中位数是(170+177)÷2=173.5;此选项正确;
D、方差= [(140﹣170)2+(160﹣170)2+(169﹣170)2+2×(170﹣170)2+3×(177﹣170)2+2×(180﹣170)2]=134.8;此选项错误;
故选:D.
9. 17 48
【解析】分析:根据平均数和方差公式的变形即可得到结果.
详解:∵一组数据x1,x2,x3,x4,x5的平均数是5,
则4x1-3,4x2-3,4x3-3,4x4-3,4x5-3的平均数是 [4(x1+x2+x3+x4+x5)-15]=17,
∵新数据是原数据的4倍减3;
∴方差变为原来数据的16倍,即48.
故填17;48.
点睛:本题考查方差的计算公式的运用:一般地设有n个数据,x1,x2,…xn,若每个数据都放大或缩小相同的倍数后再同加或同减去一个数,其平均数也有相对应的变化,方差则变为这个倍数的平方倍.
10. 7 6,7,8 3
【解析】将这组数据从小到大的顺序排列4,5,6,6,7,7,8,8,9,10,
处于中间位置的2个数是7,7,
所以由中位数的定义可知,这组数据的中位数是(7+7)÷2=7;
6、7、8各出现两次,出现的次数最多,
所以众数为6、7、8;
这组数据的平均数为: ,
所以方差为:
故答案为:7;6、7、8;3.
11.丁.
【解析】由于乙的平均数较大且方差较小,故选丁.
故答案为丁.
12.乙
【解析】∵通过观察条形统计图可知:乙的成绩更整齐,也相对更稳定,
∴甲的方差大于乙的方差,
∴乙的成绩比较稳定.
故答案为:乙.
点睛:本题考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
13.>
【解析】试题解析:观察平均气温统计图可知:乙地的平均气温比较稳定,波动小;
则乙地的日平均气温的方差小,
故S2甲>S2乙.
故答案为:>.
14.(1)3(2)2
【解析】分析:(1)根据平均数的计算公式代值计算即可;
(2)根据方差公式S2=[(x1﹣)2+(x2﹣)2+(x3﹣)2+…+(xn﹣)2],进行计算即可.
详解:(1)=(1+2+3+4+5)=3;
(2)S2= [(1﹣3)2+(2﹣3)2+(3﹣3)2+(4﹣3)2+(5﹣3)2]=2.
点睛:本题考查方差的定义与意义:一般地设n个数据:x1,x2,…,xn的平均数为,则方差S2=[x1﹣)2+(x2﹣)2+…+(xn﹣)2],它反映了一组数据的波动大小,方差越大,波动越大,反之也成立.
15.答案见解析
【解析】试题分析:(1)根据平均数、方差、中位数的概念求值,并填表;(2)根据方差分析稳定性,根据销售趋势看销售前景即可求出答案.
试题解析:
(1)
销售公司 平均数 方差 中位数 众数
甲 9 5.2 9 7
乙 9 17.0 8 8
(2)①甲、乙两个汽车销售公司去年一至十月份的销售平均数一样,都是9辆,但甲销售公司的方差较小,说明甲销售公司的销售情况更稳定。
②从甲、乙两个汽车销售公司销售数量的折线图看,乙呈上升趋势,说明乙销售公司较有潜力。
16.(1)众数为14,中位数为15;(2)见解析;(3)可以.
【解析】试题分析:(1)利用加权平均数公式求出平均数,根据众数、中位数的定义即可解决问题;
(2)判断错误.可能抽到13岁,14岁,16岁,17岁;
(3)可以.根据方差公式计算即可;
试题解析:解:(1)平均数==15,众数为14,中位数为15;
(2)判断错误.可能抽到13岁,14岁,16岁,17岁;
(3)可以.
设有n个运动员,则S2= [10% n(13﹣15)2+30% n(14﹣15)2+25% n (15﹣15)2+20% n (16﹣15)2+15% n(17﹣15)2]=1.5.
17.(1)见解析(2)选乙厂的产品
【解析】试题分析:(1)平均数就是把这组数据加起来的和除以这组数据的总数,再利用方差公式求出即可;
(2)由(1)的结果容易回答,甲厂、乙厂分别利用了平均数、方差进行广告推销,顾客在选购产品时,一般平均数相同,根据方差的大小进行选择.
试题解析:
(1)x甲=×(3+4+5+6+7)=5,
甲=×[(3-5)2+(4-5)2+(5-5)2+(6-5)2+(7-5)2]=2,
x乙=×(4+4+5+6+6)=5,
乙=×[(4-5)2+(4-5)2+(5-5)2+(6-5)2+(6-5)2]=0.8.
(2)由(1)知,甲厂、乙厂的该种电子产品在正常情况下的使用寿命平均数都是5年,
则甲厂方差>乙厂方差,选方差小的厂家的产品,
因此应选乙厂的产品.
18. 7 7.5
【解析】试题分析:(1)根据表格中的数据可以将折线统计图补充完整;
(2)根据表格中的数据可以得到乙运动员射击训练成绩的众数和中位数;
(3)根据表格中的数据可以计算出甲运动员射击成绩的平均数和方差,根据甲乙两人的方差可以得到谁的稳定性好.
试题解析:(1)由表格中的数据可以将折线统计图补充完成,如图所示,
(2)将乙的射击成绩按照从小到大排列是:
6,7,7,7,7,8,9,9,10,10,
故乙运动员射击训练成绩的众数是7,中位数是: =7.5,
故答案为:7,7.5;
(3)由表格可得,
=8,
=1.2,
∵1.5<1.8,
∴甲本次射击成绩的稳定性好,
即甲运动员射击成绩的平均数是8,方差是1.2,甲本次射击成绩的稳定性好.
19.(1)9.5,10;(2)9,1;(3)乙组.
【解析】试题分析:(1)根据中位数的定义求出最中间两个数的平均数;根据众数的定义找出出现次数最多的数即可;
(2)先求出乙组的平均成绩,再根据方差公式进行计算;
(3)先比较出甲组和乙组的方差,再根据方差的意义即可得出答案.
试题解析:(1)把甲组的成绩从小到大排列为:7,7,8,9,9,10,10,10,10,10,
最中间两个数的平均数是(9+10)÷2=9.5(分),则中位数是9.5分;
乙组成绩中10出现了4次,出现的次数最多,则乙组成绩的众数是10分;
故答案为:9.5,10;
(2)乙组的平均成绩是:(10×4+8×2+7+9×3)÷10=9,
则方差是: EMBED Equation.DSMT4 =1;
(3)∵甲组成绩的方差是1.4,乙组成绩的方差是1,
∴成绩较为整齐的是乙组.
故答案为乙组.
20.(1)3, 80, 40,金键酸牛奶销量高;(2)金键学生奶销量最稳定;(3)酸奶进80瓶,原味奶进40瓶,学生奶平时不进或少进,周末进一些.
【解析】试题分析:根据平均数、方差的计算公式计算即可,同时要注意方差越小数据越稳定.
试题解析:解:(1)学生奶=3,酸牛奶=80,原味奶=40,金键酸牛奶销量高;
(2)金键学生奶的方差=12.57;金键酸牛奶的方差=91.71;金键原味奶的方差=96.86,金键学生奶销量最稳定;
(3)酸奶进80瓶,原味奶进40瓶,学生奶平时不进或少进,周末进一些.
点睛:本题主要考查了方差的意义和用统计的知识解决实际问题.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
20.2.2 数据的离散程度同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.方差设一组数据是x1,x2,…,xn,它们的平均数是,我们用S2=[x1﹣)2+(x2﹣)2+(x3﹣)2+(x4﹣)2+(x5﹣)2])来衡量这组数据的离散程度,叫做这组数据的方差.
2.在实际问题中,常用样本方差估计总体方差,在平均数相同的情况下,方差越大,则这组数据对平均数的离散程度也越大
基础知识和能力拓展精练
一、选择题
1.有一组数据如下:2,a,3,6,5,它们的平均数是4,那么这组数据的方差是 ( )
A. 4 B. C. D. 2
2.若一组数据x1,x2,x3,x4,x5,x6的平均数是2,方差是2,则另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2,3x6﹣2的平均数和方差分别是( )
A. 2,2 B. 2,18 C. 4,6 D. 4,18
3.将一组数据中的每一个数都加上1得到一组新的数据,那么下列四个统计量中,值保持不变的是( )
A. 方差 B. 平均数 C. 中位数 D. 众数
4.一组数据:1,3,3,5,若添加一个数据3,则发生变化的统计量是( )
A. 平均数 B. 众数 C. 中位数 D. 方差
5.已知一组数据:x1,x2,x3,x4,x5,x6的平均数是2,方差是3,则另一组数据:3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2,3x6﹣2的平均数和方差分别是( )
A. 2,3 B. 2,9 C. 4,25 D. 4,27
6.某数学兴趣小组6名成员通过一次数学竞赛进行组内评比,他们的成绩分别是89,92,91,93,96,91,则关于这组数据说法正确的有( )
A. 中位数是92.5 B. 平均数是92 C. 众数是96 D. 方差是5
7.某校八年级两个班,各选派10名学生参加学校举行的“汉字听写”大赛.各参赛选手成绩的数据分析如下表所示,则以下判断错误的是( )
A. 八(2)班的总分高于八(1)班 B. 八(2)班的成绩比八(1)班稳定
C. 八(2)班的成绩集中在中上游 D. 两个班的最高分在八(2)班
8.2013年安庆市体育考试跳绳项目为学生选考项目,下表是某班模拟考试时10名同学的测试成绩(单位:个/分钟),则关于这10名同学每分钟跳绳的测试成绩,下列说法错误的是( )
成绩(个/分钟) 140 160 169 170 177 180
人数 1 1 1 2 3 2
A. 众数是177 B. 平均数是170 C. 中位数是173.5 D. 方差是135
二、填空题
9.一组数据x1,x2,x3,x4,x5的平均数是5,方差是3,则4x1﹣3,4x2﹣3,4x3﹣3,4x4﹣3,4x5﹣3的平均数是_____,方差是_____.
10.某人连续射靶10次,命中的环数分别为4,7,8,6,8,5,6,9,10,7.则他射击环数的中位数是______,众数是______,方差是______.
11.九年一班甲、乙、丙、丁四名同学几次数学测试成绩的平均数(分)及方差S2如下表:
老师想从中选派一名成绩较好且状态稳定的同学参加省初中生数学竞赛,那么应选_____.
12.如图是甲、乙两人10次射击成绩的条形统计图,则甲、乙两人成绩比较稳定的是________.
13.甲乙两地9月上旬的日平均气温如图所示,则甲乙两地这10天日平均气温方差大小关系为 (填>或<).
三、解答题
14.已知样本数据为1,2,3,4,5,求这个样本的:
(1)平均数;
(2)方差S2.(提示:S2=[x1﹣)2+(x2﹣)2+(x3﹣)2+(x4﹣)2+(x5﹣)2])
15.某市甲、乙两个汽车销售公司,去年一至十月份每月销售同种品牌汽车的情况如图所示:
(1)请你根据左图填写右表:
销售公司 平均数 方差 中位数 众数
甲 9
乙 9 17.0 8
(2)请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析:
①从平均数和方差结合看;
②从折线图上甲、乙两个汽车销售公司销售数量的趋势
看(分析哪个汽车销售公司较有潜力).
16.某射击队为了解运动员的年龄情况,作了一次年龄调查,根据射击运动员的年龄(单位:岁),绘制出如下的统计图.
(1)你能利用该统计图求出平均数、众数和中位数中的哪些统计量?并直接写出结果;
(2)小颖认为,若从该射击队中任意挑选四名队员,则必有一名队员的年龄是15岁.你认为她的判断正确吗?为什么?
(3)小亮认为,可用该统计图求出方差.你认同他的看法吗?若认同,请求出方差;若不认同,请说明理由.
17.甲、乙两个电子厂在广告中都声称他们的某种电子产品在正常情况下的使用寿命都是5年.质检部门对这两家销售的产品的使用寿命进行了跟踪调查,统计结果如下:(单位:年)
甲厂:3,4,5,6,7 乙厂:4,4,5,6,6
(1)分别求出甲、乙两厂的该种电子产品在正常情况下的使用寿命的平均数和方差;
(2)如果你是顾客,你会选购哪家电子厂的产品?说明理由.
18.甲、乙两名射击运动员在某次训练中各射击10发子弹,成绩如表:
甲 8 9 7 9 8 6 7 8 10 8
乙 6 7 9 7 9 10 8 7 7 10
且S乙2=1.8,根据上述信息完成下列问题:
(1)将甲运动员的折线统计图补充完整;
(2)乙运动员射击训练成绩的众数是_____,中位数是______.
(3)求甲运动员射击成绩的平均数和方差,并判断甲、乙两人本次射击成绩的稳定性.
19.八年2班组织了一次经典诵读比赛,甲乙两组各10人的比赛成绩如下表(10 分制):
(I)甲组数据的中位数是 ,乙组数据的众数是 ;
(Ⅱ)计算乙组数据的平均数和方差;
(Ⅲ)已知甲组数据的方差是1.4分2,则成绩较为整齐的是 .
20.小红的奶奶开了一个金键牛奶销售店,主要经营“金键学生奶”、“金键酸牛奶”、“金键原味奶”,可奶奶经营不善,经常有品种的牛奶滞销(没卖完)或脱销(量不够),造成了浪费或亏损,细心的小红结合所学的统计知识帮奶奶统计了一个星期牛奶的销售情况,并绘制了下表:
品种 星期一 星期二 星期三 星期四 星期五 星期六 星期日
金键学生奶 2 1 0 1 0 9 8
金键酸牛奶 70 70 80 75 84 81 100
金键原味奶 40 30 35 30 38 47 60
(1)计算各品种牛奶的日平均销售量,并说明哪种牛奶销量最高;
(2)计算各品种牛奶的方差(保留两位小数),并比较哪种牛奶销量最稳定;
(3)假如你是小红,你会对奶奶有哪些好的建议。
参考答案
1.D
【解析】分析:先由平均数的公式计算出a的值,再根据方差的公式计算即可.
详解:∵数据2,a,3,6,5的平均数是4,∴(2+a+3+6+5)÷5=4,∴a=4,∴这组数据的方差S2= [(2﹣4)2+(4﹣4)2+(3﹣4)2+(6﹣4)2+(5﹣4)2]=2.
故选D.
点睛:本题考查了方差的定义:一般地设n个数据,x1,x2,…xn的平均数为,则方差S2= [(x1﹣)2+(x2﹣)2+…+(xn﹣)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
2.D
【解析】分析:数据的平均数比数据的平均数的3倍少2;数据的方差是数据的方差的9倍,据此求解即可.
详解:∵数据的平均数是2,
∴数据的平均数是:
∵数据的方差是2,
∴
∴数据的方差是:
,
=18.
∴另一组数据的平均数和方差分别是4,18.
故选:D.
点睛:考查平均数和方差公式,熟练记忆和运用公式是解题的关键.
3.A
【解析】分析:根据平均数和方差的特点,一组数都加上或减去同一个不等于0的常数后,方差不变,平均数改变,即可得出答案.
详解:一组数据x1,x2,…xa的每一个数都加上同一数1,则新数据x1+1,x2+1,…xn+1的平均数改变,但是方差不变.
故选A.
点睛:本题考查了方差和平均数,一般地设n个数据,x1,x2,…xn的平均数为,则方差S2=[(x1﹣)2+(x2﹣)2+…+(xn﹣)2],掌握平均数和方差的特点是本题的关键.
4.D
【解析】解:原数据的1、3、3、5的平均数为=3,中位数为=3,众数为3,方差为×[(1﹣3)2+(3﹣3)2×2+(5﹣3)2]=2;
新数据1、3、3、3、5的平均数为=3,中位数为3,众数为3,方差为×[(1﹣3)2+(3﹣3)2×3+(5﹣3)2]=1.6;
∴添加一个数据3,方差发生变化.故选D.
5.D
【解析】解:由题知得:x1+x2+x3+x4+x5+x6=2×6=12,S12=[(x1﹣2)2+(x2﹣2)2+(x3﹣2)2+(x4﹣2)2+(x5﹣2)2+(x6﹣2)2]
=[(x12+x22+x32+x42+x52+x62)﹣4(x1+x2+x3+x4+x5+x6)+4×6]=3,∴(x12+x22+x32+x42+x52+x62)=42.
另一组数据的平均数=[3x1﹣2+3x2﹣2+3x3﹣2+3x4﹣2+3x5﹣2+3x6﹣2]=[3(x1+x2+x3+x4+x5+x6)﹣2×5]=[3×12﹣12]=×24=4,
另一组数据的方差=[(3x1﹣2﹣4)2+(3x2﹣2﹣4)2+(3x3﹣2﹣4)2+(3x4﹣2﹣4)2+(3x5﹣2﹣4)2+(3x6﹣2﹣4)2]
=[9(x12+x22+x32+x42+x52+x62)﹣36(x1+x2+x3+x4+x5+x6)+36×6]=[9×42﹣36×12+216]=×162=27.
故选D.
6.B
【解析】试题解析:这组数据按照从小到大的顺序排列为:89,91,91,92,93,96,
则中位数为: ,故A错误;
平均数为: ,故B正确;
众数为:91,故C错误;
方差S2=
=,故D错误.
故选A.
7.D
【解析】分析:根据平均数、中位数、众数和方差的性质就可以得出正确答案.
详解:根据平均分可知八(1)班的总分为940分,八(2)班的总分为950分,故A正确;八(2)班的方差小于八(1)班的方差,则八(2)班的成绩比较稳定,故B正确;根据中位数和平均分可知八(2)班的成绩集中在中上游,故C正确;最高分从这张表格上无法显示,故D错误;故本题选D.
点睛:本题主要考查的就是平均数、中位数、方差及众数的作用,属于基础题型.解决本题的关键就是要明白各数据的作用.
8.D
【解析】A、这组数据中177出现次数最多,即众数为177,此选项正确;
B、这组数据的平均数是:(140+160+169+170×2+177×3+180×2)÷10=170,此选项正确;
C、∵共有10个数,
∴中位数是第5个和6个数的平均数,
∴中位数是(170+177)÷2=173.5;此选项正确;
D、方差= [(140﹣170)2+(160﹣170)2+(169﹣170)2+2×(170﹣170)2+3×(177﹣170)2+2×(180﹣170)2]=134.8;此选项错误;
故选:D.
9. 17 48
【解析】分析:根据平均数和方差公式的变形即可得到结果.
详解:∵一组数据x1,x2,x3,x4,x5的平均数是5,
则4x1-3,4x2-3,4x3-3,4x4-3,4x5-3的平均数是 [4(x1+x2+x3+x4+x5)-15]=17,
∵新数据是原数据的4倍减3;
∴方差变为原来数据的16倍,即48.
故填17;48.
点睛:本题考查方差的计算公式的运用:一般地设有n个数据,x1,x2,…xn,若每个数据都放大或缩小相同的倍数后再同加或同减去一个数,其平均数也有相对应的变化,方差则变为这个倍数的平方倍.
10. 7 6,7,8 3
【解析】将这组数据从小到大的顺序排列4,5,6,6,7,7,8,8,9,10,
处于中间位置的2个数是7,7,
所以由中位数的定义可知,这组数据的中位数是(7+7)÷2=7;
6、7、8各出现两次,出现的次数最多,
所以众数为6、7、8;
这组数据的平均数为: ,
所以方差为:
故答案为:7;6、7、8;3.
11.丁.
【解析】由于乙的平均数较大且方差较小,故选丁.
故答案为丁.
12.乙
【解析】∵通过观察条形统计图可知:乙的成绩更整齐,也相对更稳定,
∴甲的方差大于乙的方差,
∴乙的成绩比较稳定.
故答案为:乙.
点睛:本题考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
13.>
【解析】试题解析:观察平均气温统计图可知:乙地的平均气温比较稳定,波动小;
则乙地的日平均气温的方差小,
故S2甲>S2乙.
故答案为:>.
14.(1)3(2)2
【解析】分析:(1)根据平均数的计算公式代值计算即可;
(2)根据方差公式S2=[(x1﹣)2+(x2﹣)2+(x3﹣)2+…+(xn﹣)2],进行计算即可.
详解:(1)=(1+2+3+4+5)=3;
(2)S2= [(1﹣3)2+(2﹣3)2+(3﹣3)2+(4﹣3)2+(5﹣3)2]=2.
点睛:本题考查方差的定义与意义:一般地设n个数据:x1,x2,…,xn的平均数为,则方差S2=[x1﹣)2+(x2﹣)2+…+(xn﹣)2],它反映了一组数据的波动大小,方差越大,波动越大,反之也成立.
15.答案见解析
【解析】试题分析:(1)根据平均数、方差、中位数的概念求值,并填表;(2)根据方差分析稳定性,根据销售趋势看销售前景即可求出答案.
试题解析:
(1)
销售公司 平均数 方差 中位数 众数
甲 9 5.2 9 7
乙 9 17.0 8 8
(2)①甲、乙两个汽车销售公司去年一至十月份的销售平均数一样,都是9辆,但甲销售公司的方差较小,说明甲销售公司的销售情况更稳定。
②从甲、乙两个汽车销售公司销售数量的折线图看,乙呈上升趋势,说明乙销售公司较有潜力。
16.(1)众数为14,中位数为15;(2)见解析;(3)可以.
【解析】试题分析:(1)利用加权平均数公式求出平均数,根据众数、中位数的定义即可解决问题;
(2)判断错误.可能抽到13岁,14岁,16岁,17岁;
(3)可以.根据方差公式计算即可;
试题解析:解:(1)平均数==15,众数为14,中位数为15;
(2)判断错误.可能抽到13岁,14岁,16岁,17岁;
(3)可以.
设有n个运动员,则S2= [10% n(13﹣15)2+30% n(14﹣15)2+25% n (15﹣15)2+20% n (16﹣15)2+15% n(17﹣15)2]=1.5.
17.(1)见解析(2)选乙厂的产品
【解析】试题分析:(1)平均数就是把这组数据加起来的和除以这组数据的总数,再利用方差公式求出即可;
(2)由(1)的结果容易回答,甲厂、乙厂分别利用了平均数、方差进行广告推销,顾客在选购产品时,一般平均数相同,根据方差的大小进行选择.
试题解析:
(1)x甲=×(3+4+5+6+7)=5,
甲=×[(3-5)2+(4-5)2+(5-5)2+(6-5)2+(7-5)2]=2,
x乙=×(4+4+5+6+6)=5,
乙=×[(4-5)2+(4-5)2+(5-5)2+(6-5)2+(6-5)2]=0.8.
(2)由(1)知,甲厂、乙厂的该种电子产品在正常情况下的使用寿命平均数都是5年,
则甲厂方差>乙厂方差,选方差小的厂家的产品,
因此应选乙厂的产品.
18. 7 7.5
【解析】试题分析:(1)根据表格中的数据可以将折线统计图补充完整;
(2)根据表格中的数据可以得到乙运动员射击训练成绩的众数和中位数;
(3)根据表格中的数据可以计算出甲运动员射击成绩的平均数和方差,根据甲乙两人的方差可以得到谁的稳定性好.
试题解析:(1)由表格中的数据可以将折线统计图补充完成,如图所示,
(2)将乙的射击成绩按照从小到大排列是:
6,7,7,7,7,8,9,9,10,10,
故乙运动员射击训练成绩的众数是7,中位数是: =7.5,
故答案为:7,7.5;
(3)由表格可得,
=8,
=1.2,
∵1.5<1.8,
∴甲本次射击成绩的稳定性好,
即甲运动员射击成绩的平均数是8,方差是1.2,甲本次射击成绩的稳定性好.
19.(1)9.5,10;(2)9,1;(3)乙组.
【解析】试题分析:(1)根据中位数的定义求出最中间两个数的平均数;根据众数的定义找出出现次数最多的数即可;
(2)先求出乙组的平均成绩,再根据方差公式进行计算;
(3)先比较出甲组和乙组的方差,再根据方差的意义即可得出答案.
试题解析:(1)把甲组的成绩从小到大排列为:7,7,8,9,9,10,10,10,10,10,
最中间两个数的平均数是(9+10)÷2=9.5(分),则中位数是9.5分;
乙组成绩中10出现了4次,出现的次数最多,则乙组成绩的众数是10分;
故答案为:9.5,10;
(2)乙组的平均成绩是:(10×4+8×2+7+9×3)÷10=9,
则方差是: EMBED Equation.DSMT4 =1;
(3)∵甲组成绩的方差是1.4,乙组成绩的方差是1,
∴成绩较为整齐的是乙组.
故答案为乙组.
20.(1)3, 80, 40,金键酸牛奶销量高;(2)金键学生奶销量最稳定;(3)酸奶进80瓶,原味奶进40瓶,学生奶平时不进或少进,周末进一些.
【解析】试题分析:根据平均数、方差的计算公式计算即可,同时要注意方差越小数据越稳定.
试题解析:解:(1)学生奶=3,酸牛奶=80,原味奶=40,金键酸牛奶销量高;
(2)金键学生奶的方差=12.57;金键酸牛奶的方差=91.71;金键原味奶的方差=96.86,金键学生奶销量最稳定;
(3)酸奶进80瓶,原味奶进40瓶,学生奶平时不进或少进,周末进一些.
点睛:本题主要考查了方差的意义和用统计的知识解决实际问题.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
