第20章 数据的初步分析单元检测A卷(含解析)
文档属性
| 名称 | 第20章 数据的初步分析单元检测A卷(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 703.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-09 00:00:00 | ||
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
第20章数据的初步分析单元检测A卷
班级__________姓名____________总分___________
一、选择题
1.某居民区的月底统计用电情况如下,其中3户用电45度,5户用电50度,6户用电42度,则平均用电( )度.
A. 41 B. 42 C. 45.5 D. 46
2.甲、乙、丙三种糖果售价分别为每千克6元,7元,8元,若将甲种8千克,乙种10千克,丙种3千克混在一起,则售价应定为每千克( ).
A. 6.7元 B. 6.8元 C. 7.5元 D. 8.6元
3.某校9名初中毕业生的中考体育考试成绩如下:25 26 26 26 26 27 28 29 29,这些成绩的中位数是( )
A.25 B.26 C.26.5 D.30
4.甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩都为9环,方差分别为S甲2=0.56,S乙2=0.62,S丙2=0.39,S丁2=0.42,则四人中成绩最稳定的是( )
A. 甲 B. 乙 C. 丙 D. 丁
5.在100个数据中,用适当的方法,抽取50个作为样本进行统计,频数分布表中55~58这一组数据的频率是0.12,那么估计这100个数据中,落在55~58之间的约有( )
A. 120个 B. 60个 C. 12个 D. 6个
6.如果一组数据3,x,7,8,11的平均数为7,那么x为( )
A. 5 B. 6 C. 7 D. 8
7.数据共40个,分为6组,第1到第四组的频数分别为10,5,7,6,第5组的频率为0.1,则第6组的频数为( )
A、4 B、10 C、6 D、8
8.16位参加百米半决赛同学的成绩各不相同, 按成绩取前8位进入决赛. 如果小刘知道了自己的成绩后,要判断能否进入决赛,其他15位同学成绩的下列数据中,能使他得出结论的是( )
A. 平均数 B. 众数 C. 中位数 D. 方差
9.在一次歌咏比赛中,某选手的得分情况如下:92,88,95,93,96,95,94.这组数据的众数和中位数分别是( )
A.94,94 B.95,95 C.94,95 D.95,94
10.已知一个样本a , 4,2,5,3,它的平均数是3,则这个样本的标准差为( ).
A. 0 B. 1 C. D. 2
二、填空题
11.在一组数据中,出现次数最多的数据叫做这组数据的________.
12.一个小组有10名学生,他们年龄构成如下表,(单位:岁)则这个小组学生平均年龄为________.
13.为了解社区居民的用水情况,小江调查了120户居民,发现人均日用水量在基本标准量(50升)范围内的频率是75%,那么他所调查的居民超出了标准量的有________ 户.
14.已知一组数据﹣3,x,﹣2,3,1,6的中位数为1,则其方差为 .
15.若数据2,3,﹣1,7,x的平均数为2,则x= .
16.已知一组数据x1,x2,x3,x4,x 5的平均数是2,方差是,那么另一组数据3x1-2,3x2-2,3x3-2,3x4-2,3x 5-2的平均数是________,方差是________.
三、解答题
17.一组数据有30个数,把它们分成四组,其中第一组,第二组的频数分别为7,9,第三组的频率为0.1,则第四组的频数是多少?
18.某酒店共有6名员工,所有员工的工资如下表所示:
人 员 经理 会计 厨师 服务员1 服务员2 勤杂工
月工资(元) 6000 3000 4000 2000 2000 1000
(1)酒店所有员工的平均月工资是多少元?中位数、众数各是多少?
(2)平均月工资能准确反映该酒店员工工资的一般水平吗?若能,请说明理由.若不能,如何才能较准确地反映该酒店员工工资的一般水平?谈谈你的看法.
19.随着车辆的增加,交通违规的现象越来越严重,交警对某雷达测速区检测到的一组汽车的时速数据进行整理,得到其未完成的频数及频率如表(每个数据段含前面数字,不含后面数字):
(1)请你把表中的数据填写完整;
数据段 频数 频率
30﹣40 10 0.05
40﹣50 36
50﹣60 0.39
60﹣70
70﹣80 20 0.10
总计 200 1
(2)如果汽车时速不低于60千米即为违章,则违章车辆共有多少辆?
20.某商场统计了每个营业员在某月的销售额,绘制了如下的条形统计图以及不完整的扇形统计图:
解答下列问题:
(1)设营业员的月销售额为x(单位:万元),商场规定:当x<15时为不称职,当15≤x<20时,为基本称职,当20≤x<25为称职,当x≥25时为优秀.则扇形统计图中的a=________,b=________.
(2)所有营业员月销售额的中位数和众数分别是多少?
(3)为了调动营业员的积极性,决定制定一个月销售额奖励标准,凡到达或超过这个标准的营业员将受到奖励.如果要使得营业员的半数左右能获奖,奖励标准应定为多少万元?并简述其理由.
21.我校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
组别 正确数字x 人数
A 0≤x<8 10
B 8≤x<16 15
C 16≤x<24 25
D 24≤x<32 m
E 32≤x<40 n
根据以上信息解决下列问题:
(1)在统计表中,m= ,n= ,并补全条形统计图.
(2)扇形统计图中“C组”所对应的圆心角的度数是 .
(3)有三位评委老师,每位老师在E组学生完成学校比赛后,出示“通过”或“淘汰”或“待定”的评定结果.学校规定:每位学生至少获得两位评委老师的“通过”才能代表学校参加鄂州市“汉字听写”比赛,请用树形图求出E组学生王云参加鄂州市“汉字听写”比赛的概率.
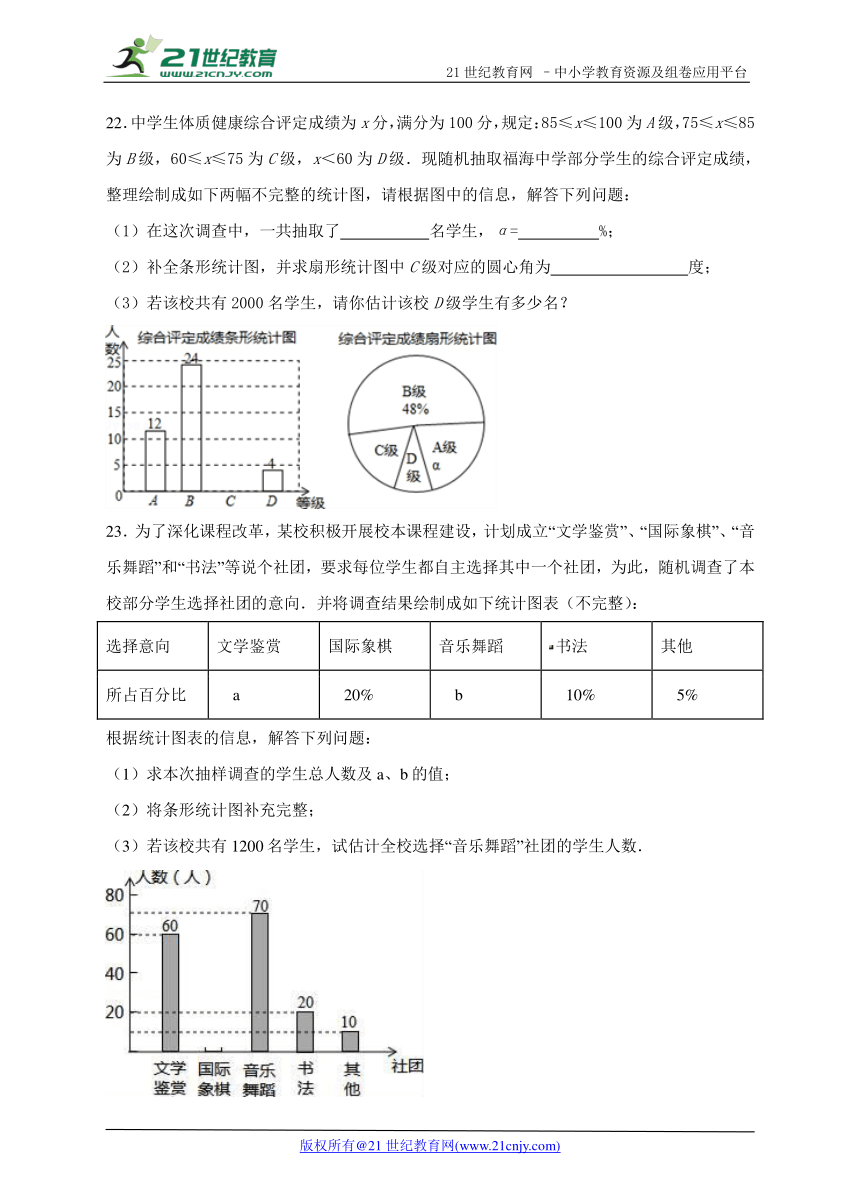
22.中学生体质健康综合评定成绩为x分,满分为100分,规定:85≤x≤100为A级,75≤x≤85为B级,60≤x≤75为C级,x<60为D级.现随机抽取福海中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图,请根据图中的信息,解答下列问题:
(1)在这次调查中,一共抽取了 名学生,α= %;
(2)补全条形统计图,并求扇形统计图中C级对应的圆心角为 度;
(3)若该校共有2000名学生,请你估计该校D级学生有多少名?
23.为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“国际象棋”、“音乐舞蹈”和“书法”等说个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了本校部分学生选择社团的意向.并将调查结果绘制成如下统计图表(不完整):
选择意向 文学鉴赏 国际象棋 音乐舞蹈 书法 其他
所占百分比 a 20% b 10% 5%
根据统计图表的信息,解答下列问题:
(1)求本次抽样调查的学生总人数及a、b的值;
(2)将条形统计图补充完整;
(3)若该校共有1200名学生,试估计全校选择“音乐舞蹈”社团的学生人数.
24.某兴趣小组为了了解本校男生参加课外体育锻炼情况,随机抽取本校300名男生进行了问卷调查,统计整理并绘制了如下两幅尚不完整的统计图.
请根据以上信息解答下列问题:
课外体育锻炼情况扇形统计图中,“经常参加”所对应的圆心角的度数为______;
请补全条形统计图;
该校共有1200名男生,请估计全校男生中经常参加课外体育锻炼并且最喜欢的项目是篮球的人数;
小明认为“全校所有男生中,课外最喜欢参加的运动项目是乒乓球的人数约为”,请你判断这种说法是否正确,并说明理由.
参考答案
1.C
【解析】由题意可得:(度).
故选C.
2.B
【解析】由题意可得:(元).
故选B.
3.B
【解析】
试题分析:中位数的求法:把数据重新排列,从大到小或从小到大,如果是奇数个数据,则中间一个数是中位数;如果是偶数个数据,则中间两个数的平均数是中位数。
由题意得这些成绩的中位数是26,故选B.
点评:本题属于基础应用题,只需学生熟练掌握中位数的求法,即可完成.
4.C
【解析】∵方差越小数据组中的数据越稳定,而四名同学这10射击的方差中,最小的是S丙2=0.39,
∴这四人中丙的成绩最稳定.
故选C.
5.C
【解析】试题解析:用样本估计总体:在频数分布表中,55 58这一组的频率是0.12,
那么估计总体数据落在55 58这一组的频率同样是0.12,
那么其大约有50×0.12=6个,
所以100个数据中,落在55 58之间的约有12个.
故选C.
6.B
【解析】
试题分析:根据算术平均数的计算公式,先列出算式,再求出x的值即可.
解:∵一组数据3,x,7,8,11的平均数为7,
∴(3+x+7+8+11)÷5=7,
解得x=6;
故选 B.
点评:此题考查了算术平均数,掌握算术平均数的计算公式是本题的关键,是一道基础题.
7.D
【解析】第5组的频数为40×0.1=4;
∴第6组的频数为40-(10+5+7+6+4)=8.
故本题选D.
8.C
【解析】∵其他15同学成绩的中位数刚好是从高分到低分排列的第8名,
∴他只需要知道其他15位同学成绩的中位数就可以知道自己能否进入决赛了.
故选C.
9.D
【解析】
试题分析:根据众数、中位数的定义求解即可.
解:这组数据按顺序排列为:88,92,93,94,95,95,96,
故众数为:95,
中位数为:94.
故选D.
【点评】本题考查了众数和中位数的知识,属于基础题,解答本题的关键是熟练掌握众数和中位数的定义.
10.C
【解析】由题意得:,解得:,
∴这个样本的标准差=.
故选C.
点睛:(1)一组数据的标准差是这组数据方差的算术平方根;(2)一组数据的方差计算公式为:S2=,其中“S2”表示该组数据的方程,到表示数据组中的每个数据,表示该组数据的平均数.
11.众数
【解析】根据“众数”的定义可知:一组数据中出现次数最多的数据叫这组数据的众数.
故答案为:众数.
12.13.4岁
【解析】由题意得,这个小组学生的平均年龄=(岁).
故答案为:13.4 .
13.30
【解析】由题意可得:120×(1-75%)=120×25%=30(户).
故答案为:30.
14.9
【解析】试题分析:∵数据﹣3,x,﹣2,3,1,6的中位数为1,∴ EMBED Equation.DSMT4 ,解得x=1,∴数据的平均数=(﹣3﹣2+1+1+3+6)=1,∴方差= [(﹣3﹣1)2+(﹣2﹣1)2+(1﹣1)2+(1﹣1)2+(3﹣1)2+(6﹣1)2]=9.故答案为:9.
15.-1
【解析】
根据平均数的计算方法,可得出方程,解出即可得出答案.
解:由题意得,(2+3﹣1+7+x)=2,
解得:x=﹣1.
故答案为:﹣1.
16. 4 3
【解析】因为将一组数据每个数都乘以同一个数得到新的一组数据的平均数扩大相应的倍数,一组数据每个数同时减去一个数得到新的一组数据平均数要减去同样的数,所以平均数是4,因为一组数据每个数同时加上或减去一个数得到新的一组数据的方差不变,一组数据的每个数都乘以同一个数得到新的一组数据的方差要乘以这个数的平方,所以新的这组数据的方差是3,故答案为:4,3.
17.11
【解析】试题分析:
由题意可得:第三组的频数=30×0.1=3,由此结合已知数据可得第四组的频数=30-7-9-3=11.
试题解析:
第三组的频数为:30×0.1=3,
则第四组的频数=30﹣7﹣9﹣3=11.
18.(1)平均月工3000(元),众数为2000元,中位数2500元;
(2)这组数据的众数是2000元,才能较准确地反映该酒店员工工资的一般水平,原因是它符合多数人的工资水平.
【解析】试题分析:(1)根据平均数的计算公式,直接求出酒店所有员工的平均月工资即可;
(2)由平均数的值,可见平均月工资不能准确反映该酒店员工工资的一般水平,反映该酒店员工工资的一般水平的统计量应符合多数人的工资水平才可以.
试题解析:解:(1)平均月工资=(6000+3000+4000+2000+2000+1000)÷6=3000(元),众数为2000元,中位数2500元;
(2)∵能达到这个工资水平的只有3人,∴平均月工资不能准确反映该酒店员工工资的一般水平,这组数据的众数是2000元,才能较准确地反映该酒店员工工资的一般水平,原因是它符合多数人的工资水平.
点睛:本题考查了平均数的计算及众数、中位数的知识,以及统计量的正确选择,解题的关键是能够了解众数及中位数的意义,难度不大.
19.(1)见解析;(2)76
【解析】试题分析:
(1)由表格中的已知数据可得:40-50组的频率=36÷200=0.18;50-60组的频数为:200×0.39=78;60-70组的频数=200-10-36-78-20=56;60-70组的频率=56÷200=0.28;将计算结果填入表格中的相应位置即可;
(2)由(1)中计算结果表格中原有的已知数据可得:违章车辆数=56+20=76(辆).
试题解析:
(1)由题意可得:36÷200=0.18,200×0.39=78,200﹣10﹣36﹣78﹣20=56,56÷200=0.28;
将所缺数据补充完整的表格为:
数据段 频数 频率
30﹣40 10 0.05
40﹣50 36 0.18
50﹣60 78 0.39
60﹣70 56 0.28
70﹣80 20 0.10
总计 200 1
(2)由题意可得:56+20=76(辆),
答:违章车辆有76辆.
20.(1)10;60;(2)中位数为21、众数为20;(3)奖励标准应定为21万元,理由见解析
【解析】试题分析:
(1)由统计图中的信息可知:不称职的有2人,占总数的6.7%,由此可得总人数为:2÷6.7%=30(人);而条形统计图中的信息显示:优秀的有3人,称职的有18人,由此可得3÷30×100%=10%,18÷30×100%=60%,即a=10,b=60;
(2)由条形统计图可知,这组数据的众数为20,中位数是按大小排列后的第15和16个数据的平均数,而由第15和16个数据都是21可知中位数是21;
(3)由题意可知:奖励标准应该定为21万元,因为由(2)可知,这组数据的中位数是21万,因此按要使一半左右的人获得奖励,应该以中位数作为奖励的标准.
试题解析:
(1)由统计图中信息可得:该商场进入统计的营业员总数=2÷6.7%=30(人);
∵优秀的有3人,
∴a%=3÷30×100%=10%,
∴a=10;
∵称职的有18人,
∴b%=18÷30×100%=60%,
∴b=60;
(2)由条形统计图可知,这组数据的众数为20;
由条件下统计图可知,这30个数据按从小到大排列后,第15个数和第16个数都是21,
∴这组数据的中位数为21;
(3)∵要使一半左右的人获得奖励,
∴奖励标准应该以中位数为准,
∴奖励标准应定为21万元.
点睛:这是一道综合应用条形统计图和扇形统计图中的信息来解决相关问题的统计图,解题的关键是弄清两幅统计图中数据间的对应关系,再进行细心计算即可.
21.(1)m=30, n=20,图详见解析;(2)90°;(3).
【解析】分析:(1)、根据B的人数和百分比得出总人数,从而根据总人数分别求出m和n的值;(2)、根据C的人数和总人数的比值得出扇形的圆心角度数;(3)、首先根据题意画出树状图,然后根据概率的计算法则得出答案.
详解:(1)∵总人数为15÷15%=100(人),
∴D组人数m=100×30%=30,E组人数n=100×20%=20,
补全条形图如下:
(2)扇形统计图中“C组”所对应的圆心角的度数是360°×=90°,
(3)记通过为A、淘汰为B、待定为C,
画树状图如下:
由树状图可知,共有27种等可能结果,其中获得两位评委老师的“通过”有7种情况,
∴E组学生王云参加鄂州市“汉字听写”比赛的概率为.
点睛:本题主要考查的就是扇形统计图、条形统计图以及概率的计算法则,属于基础题型.解决这个问题,我们一定要明白样本容量=频数÷频率,根据这个公式即可进行求解.
22.(1)50,24 ; (2)72°; (3)160名
【解析】分析:(1)根据B级的人数和所占的百分比求出抽取的总人数,再用A级的人数除以总数即可求出a;
(2)用抽取的总人数减去A、B、D的人数,求出C级的人数,从而补全统计图;用360度乘以C级所占的百分比即可求出扇形统计图中C级对应的圆心角的度数;
(3)用D级所占的百分比乘以该校的总人数,即可得出该校D级的学生数.
详解:(1)在这次调查中,一共抽取的学生数是: =50(人),a=×100%=24%;
故答案为:50,24;
(2)等级为C的人数是:50﹣12﹣24﹣4=10(人),补图如下:
扇形统计图中C级对应的圆心角为×360°=72°;
故答案为:72;
(3)根据题意得:2000×=160(人).
答:该校D级学生有160人.
点睛:本题考查了是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
23.(1)本次抽样调查的学生总人数是200,a=30%,b=35%;(2)补图见解析;(3)全校选择“音乐舞蹈”社团的学生人数大约有420人.
【解析】分析:(1)美好“书法”社团有20人占10%求抽样调查的人数,分别用60,70除以调查的人数再乘以100%;(2)求出“国际象棋”社团的人数即可画条形图;(3)用“音乐舞蹈”社团的人数的百分比乘以全校学生人数.
详解:(1)本次抽样调查的学生总人数是:20÷10%=200,
a=×100%=30%,
b=×100%=35%.
(2)国际象棋的人数是:200×20%=40,
条形统计图补充如下:
(3)1200×35%=420人,
答:全校选择“音乐舞蹈”社团的学生人数大约有420人.
点睛:本题主要考查了条形统计图与用样本估计总体,从条形统计图和统计表格中获取有用的信息是解决这类问题的关键.
24.;补图见解析;全校男生中经常参加课外体育锻炼并且最喜欢的项目是篮球的人数约为人;这个说法不正确,理由见解析.
【解析】分析:(1)用“经常参加”所占的百分比乘以360°计算即可得解;
(2)先求出“经常参加”的人数,然后求出喜欢篮球的人数,再补全统计图即可;
(3)用总人数乘以喜欢篮球的学生所占的百分比计算即可得解;
(4)根据喜欢乒乓球的27人都是“经常参加”的学生,“偶尔参加”的学生中也会有喜欢乒乓球的考虑解答.
详解:(1)360°×(1﹣15%﹣45%)=360°×40%=144°;
故答案为:144°;
(2)“经常参加”的人数为:300×40%=120人,喜欢篮球的学生人数为:120﹣27﹣33﹣20=120﹣80=40人;
补全统计图如图所示;
(3)全校男生中经常参加课外体育锻炼并且最喜欢的项目是篮球的人数约为:1200×=160人;
(4)这个说法不正确.
理由如下:小明得到的108人是全校经常参加课外体育锻炼的男生中最喜欢的项目是乒乓球的人数,而全校偶尔参加课外体育锻炼的男生中也会有最喜欢乒乓球的,因此应多于108人.
点睛:本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
第20章数据的初步分析单元检测A卷
班级__________姓名____________总分___________
一、选择题
1.某居民区的月底统计用电情况如下,其中3户用电45度,5户用电50度,6户用电42度,则平均用电( )度.
A. 41 B. 42 C. 45.5 D. 46
2.甲、乙、丙三种糖果售价分别为每千克6元,7元,8元,若将甲种8千克,乙种10千克,丙种3千克混在一起,则售价应定为每千克( ).
A. 6.7元 B. 6.8元 C. 7.5元 D. 8.6元
3.某校9名初中毕业生的中考体育考试成绩如下:25 26 26 26 26 27 28 29 29,这些成绩的中位数是( )
A.25 B.26 C.26.5 D.30
4.甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩都为9环,方差分别为S甲2=0.56,S乙2=0.62,S丙2=0.39,S丁2=0.42,则四人中成绩最稳定的是( )
A. 甲 B. 乙 C. 丙 D. 丁
5.在100个数据中,用适当的方法,抽取50个作为样本进行统计,频数分布表中55~58这一组数据的频率是0.12,那么估计这100个数据中,落在55~58之间的约有( )
A. 120个 B. 60个 C. 12个 D. 6个
6.如果一组数据3,x,7,8,11的平均数为7,那么x为( )
A. 5 B. 6 C. 7 D. 8
7.数据共40个,分为6组,第1到第四组的频数分别为10,5,7,6,第5组的频率为0.1,则第6组的频数为( )
A、4 B、10 C、6 D、8
8.16位参加百米半决赛同学的成绩各不相同, 按成绩取前8位进入决赛. 如果小刘知道了自己的成绩后,要判断能否进入决赛,其他15位同学成绩的下列数据中,能使他得出结论的是( )
A. 平均数 B. 众数 C. 中位数 D. 方差
9.在一次歌咏比赛中,某选手的得分情况如下:92,88,95,93,96,95,94.这组数据的众数和中位数分别是( )
A.94,94 B.95,95 C.94,95 D.95,94
10.已知一个样本a , 4,2,5,3,它的平均数是3,则这个样本的标准差为( ).
A. 0 B. 1 C. D. 2
二、填空题
11.在一组数据中,出现次数最多的数据叫做这组数据的________.
12.一个小组有10名学生,他们年龄构成如下表,(单位:岁)则这个小组学生平均年龄为________.
13.为了解社区居民的用水情况,小江调查了120户居民,发现人均日用水量在基本标准量(50升)范围内的频率是75%,那么他所调查的居民超出了标准量的有________ 户.
14.已知一组数据﹣3,x,﹣2,3,1,6的中位数为1,则其方差为 .
15.若数据2,3,﹣1,7,x的平均数为2,则x= .
16.已知一组数据x1,x2,x3,x4,x 5的平均数是2,方差是,那么另一组数据3x1-2,3x2-2,3x3-2,3x4-2,3x 5-2的平均数是________,方差是________.
三、解答题
17.一组数据有30个数,把它们分成四组,其中第一组,第二组的频数分别为7,9,第三组的频率为0.1,则第四组的频数是多少?
18.某酒店共有6名员工,所有员工的工资如下表所示:
人 员 经理 会计 厨师 服务员1 服务员2 勤杂工
月工资(元) 6000 3000 4000 2000 2000 1000
(1)酒店所有员工的平均月工资是多少元?中位数、众数各是多少?
(2)平均月工资能准确反映该酒店员工工资的一般水平吗?若能,请说明理由.若不能,如何才能较准确地反映该酒店员工工资的一般水平?谈谈你的看法.
19.随着车辆的增加,交通违规的现象越来越严重,交警对某雷达测速区检测到的一组汽车的时速数据进行整理,得到其未完成的频数及频率如表(每个数据段含前面数字,不含后面数字):
(1)请你把表中的数据填写完整;
数据段 频数 频率
30﹣40 10 0.05
40﹣50 36
50﹣60 0.39
60﹣70
70﹣80 20 0.10
总计 200 1
(2)如果汽车时速不低于60千米即为违章,则违章车辆共有多少辆?
20.某商场统计了每个营业员在某月的销售额,绘制了如下的条形统计图以及不完整的扇形统计图:
解答下列问题:
(1)设营业员的月销售额为x(单位:万元),商场规定:当x<15时为不称职,当15≤x<20时,为基本称职,当20≤x<25为称职,当x≥25时为优秀.则扇形统计图中的a=________,b=________.
(2)所有营业员月销售额的中位数和众数分别是多少?
(3)为了调动营业员的积极性,决定制定一个月销售额奖励标准,凡到达或超过这个标准的营业员将受到奖励.如果要使得营业员的半数左右能获奖,奖励标准应定为多少万元?并简述其理由.
21.我校举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分.
组别 正确数字x 人数
A 0≤x<8 10
B 8≤x<16 15
C 16≤x<24 25
D 24≤x<32 m
E 32≤x<40 n
根据以上信息解决下列问题:
(1)在统计表中,m= ,n= ,并补全条形统计图.
(2)扇形统计图中“C组”所对应的圆心角的度数是 .
(3)有三位评委老师,每位老师在E组学生完成学校比赛后,出示“通过”或“淘汰”或“待定”的评定结果.学校规定:每位学生至少获得两位评委老师的“通过”才能代表学校参加鄂州市“汉字听写”比赛,请用树形图求出E组学生王云参加鄂州市“汉字听写”比赛的概率.
22.中学生体质健康综合评定成绩为x分,满分为100分,规定:85≤x≤100为A级,75≤x≤85为B级,60≤x≤75为C级,x<60为D级.现随机抽取福海中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图,请根据图中的信息,解答下列问题:
(1)在这次调查中,一共抽取了 名学生,α= %;
(2)补全条形统计图,并求扇形统计图中C级对应的圆心角为 度;
(3)若该校共有2000名学生,请你估计该校D级学生有多少名?
23.为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“国际象棋”、“音乐舞蹈”和“书法”等说个社团,要求每位学生都自主选择其中一个社团,为此,随机调查了本校部分学生选择社团的意向.并将调查结果绘制成如下统计图表(不完整):
选择意向 文学鉴赏 国际象棋 音乐舞蹈 书法 其他
所占百分比 a 20% b 10% 5%
根据统计图表的信息,解答下列问题:
(1)求本次抽样调查的学生总人数及a、b的值;
(2)将条形统计图补充完整;
(3)若该校共有1200名学生,试估计全校选择“音乐舞蹈”社团的学生人数.
24.某兴趣小组为了了解本校男生参加课外体育锻炼情况,随机抽取本校300名男生进行了问卷调查,统计整理并绘制了如下两幅尚不完整的统计图.
请根据以上信息解答下列问题:
课外体育锻炼情况扇形统计图中,“经常参加”所对应的圆心角的度数为______;
请补全条形统计图;
该校共有1200名男生,请估计全校男生中经常参加课外体育锻炼并且最喜欢的项目是篮球的人数;
小明认为“全校所有男生中,课外最喜欢参加的运动项目是乒乓球的人数约为”,请你判断这种说法是否正确,并说明理由.
参考答案
1.C
【解析】由题意可得:(度).
故选C.
2.B
【解析】由题意可得:(元).
故选B.
3.B
【解析】
试题分析:中位数的求法:把数据重新排列,从大到小或从小到大,如果是奇数个数据,则中间一个数是中位数;如果是偶数个数据,则中间两个数的平均数是中位数。
由题意得这些成绩的中位数是26,故选B.
点评:本题属于基础应用题,只需学生熟练掌握中位数的求法,即可完成.
4.C
【解析】∵方差越小数据组中的数据越稳定,而四名同学这10射击的方差中,最小的是S丙2=0.39,
∴这四人中丙的成绩最稳定.
故选C.
5.C
【解析】试题解析:用样本估计总体:在频数分布表中,55 58这一组的频率是0.12,
那么估计总体数据落在55 58这一组的频率同样是0.12,
那么其大约有50×0.12=6个,
所以100个数据中,落在55 58之间的约有12个.
故选C.
6.B
【解析】
试题分析:根据算术平均数的计算公式,先列出算式,再求出x的值即可.
解:∵一组数据3,x,7,8,11的平均数为7,
∴(3+x+7+8+11)÷5=7,
解得x=6;
故选 B.
点评:此题考查了算术平均数,掌握算术平均数的计算公式是本题的关键,是一道基础题.
7.D
【解析】第5组的频数为40×0.1=4;
∴第6组的频数为40-(10+5+7+6+4)=8.
故本题选D.
8.C
【解析】∵其他15同学成绩的中位数刚好是从高分到低分排列的第8名,
∴他只需要知道其他15位同学成绩的中位数就可以知道自己能否进入决赛了.
故选C.
9.D
【解析】
试题分析:根据众数、中位数的定义求解即可.
解:这组数据按顺序排列为:88,92,93,94,95,95,96,
故众数为:95,
中位数为:94.
故选D.
【点评】本题考查了众数和中位数的知识,属于基础题,解答本题的关键是熟练掌握众数和中位数的定义.
10.C
【解析】由题意得:,解得:,
∴这个样本的标准差=.
故选C.
点睛:(1)一组数据的标准差是这组数据方差的算术平方根;(2)一组数据的方差计算公式为:S2=,其中“S2”表示该组数据的方程,到表示数据组中的每个数据,表示该组数据的平均数.
11.众数
【解析】根据“众数”的定义可知:一组数据中出现次数最多的数据叫这组数据的众数.
故答案为:众数.
12.13.4岁
【解析】由题意得,这个小组学生的平均年龄=(岁).
故答案为:13.4 .
13.30
【解析】由题意可得:120×(1-75%)=120×25%=30(户).
故答案为:30.
14.9
【解析】试题分析:∵数据﹣3,x,﹣2,3,1,6的中位数为1,∴ EMBED Equation.DSMT4 ,解得x=1,∴数据的平均数=(﹣3﹣2+1+1+3+6)=1,∴方差= [(﹣3﹣1)2+(﹣2﹣1)2+(1﹣1)2+(1﹣1)2+(3﹣1)2+(6﹣1)2]=9.故答案为:9.
15.-1
【解析】
根据平均数的计算方法,可得出方程,解出即可得出答案.
解:由题意得,(2+3﹣1+7+x)=2,
解得:x=﹣1.
故答案为:﹣1.
16. 4 3
【解析】因为将一组数据每个数都乘以同一个数得到新的一组数据的平均数扩大相应的倍数,一组数据每个数同时减去一个数得到新的一组数据平均数要减去同样的数,所以平均数是4,因为一组数据每个数同时加上或减去一个数得到新的一组数据的方差不变,一组数据的每个数都乘以同一个数得到新的一组数据的方差要乘以这个数的平方,所以新的这组数据的方差是3,故答案为:4,3.
17.11
【解析】试题分析:
由题意可得:第三组的频数=30×0.1=3,由此结合已知数据可得第四组的频数=30-7-9-3=11.
试题解析:
第三组的频数为:30×0.1=3,
则第四组的频数=30﹣7﹣9﹣3=11.
18.(1)平均月工3000(元),众数为2000元,中位数2500元;
(2)这组数据的众数是2000元,才能较准确地反映该酒店员工工资的一般水平,原因是它符合多数人的工资水平.
【解析】试题分析:(1)根据平均数的计算公式,直接求出酒店所有员工的平均月工资即可;
(2)由平均数的值,可见平均月工资不能准确反映该酒店员工工资的一般水平,反映该酒店员工工资的一般水平的统计量应符合多数人的工资水平才可以.
试题解析:解:(1)平均月工资=(6000+3000+4000+2000+2000+1000)÷6=3000(元),众数为2000元,中位数2500元;
(2)∵能达到这个工资水平的只有3人,∴平均月工资不能准确反映该酒店员工工资的一般水平,这组数据的众数是2000元,才能较准确地反映该酒店员工工资的一般水平,原因是它符合多数人的工资水平.
点睛:本题考查了平均数的计算及众数、中位数的知识,以及统计量的正确选择,解题的关键是能够了解众数及中位数的意义,难度不大.
19.(1)见解析;(2)76
【解析】试题分析:
(1)由表格中的已知数据可得:40-50组的频率=36÷200=0.18;50-60组的频数为:200×0.39=78;60-70组的频数=200-10-36-78-20=56;60-70组的频率=56÷200=0.28;将计算结果填入表格中的相应位置即可;
(2)由(1)中计算结果表格中原有的已知数据可得:违章车辆数=56+20=76(辆).
试题解析:
(1)由题意可得:36÷200=0.18,200×0.39=78,200﹣10﹣36﹣78﹣20=56,56÷200=0.28;
将所缺数据补充完整的表格为:
数据段 频数 频率
30﹣40 10 0.05
40﹣50 36 0.18
50﹣60 78 0.39
60﹣70 56 0.28
70﹣80 20 0.10
总计 200 1
(2)由题意可得:56+20=76(辆),
答:违章车辆有76辆.
20.(1)10;60;(2)中位数为21、众数为20;(3)奖励标准应定为21万元,理由见解析
【解析】试题分析:
(1)由统计图中的信息可知:不称职的有2人,占总数的6.7%,由此可得总人数为:2÷6.7%=30(人);而条形统计图中的信息显示:优秀的有3人,称职的有18人,由此可得3÷30×100%=10%,18÷30×100%=60%,即a=10,b=60;
(2)由条形统计图可知,这组数据的众数为20,中位数是按大小排列后的第15和16个数据的平均数,而由第15和16个数据都是21可知中位数是21;
(3)由题意可知:奖励标准应该定为21万元,因为由(2)可知,这组数据的中位数是21万,因此按要使一半左右的人获得奖励,应该以中位数作为奖励的标准.
试题解析:
(1)由统计图中信息可得:该商场进入统计的营业员总数=2÷6.7%=30(人);
∵优秀的有3人,
∴a%=3÷30×100%=10%,
∴a=10;
∵称职的有18人,
∴b%=18÷30×100%=60%,
∴b=60;
(2)由条形统计图可知,这组数据的众数为20;
由条件下统计图可知,这30个数据按从小到大排列后,第15个数和第16个数都是21,
∴这组数据的中位数为21;
(3)∵要使一半左右的人获得奖励,
∴奖励标准应该以中位数为准,
∴奖励标准应定为21万元.
点睛:这是一道综合应用条形统计图和扇形统计图中的信息来解决相关问题的统计图,解题的关键是弄清两幅统计图中数据间的对应关系,再进行细心计算即可.
21.(1)m=30, n=20,图详见解析;(2)90°;(3).
【解析】分析:(1)、根据B的人数和百分比得出总人数,从而根据总人数分别求出m和n的值;(2)、根据C的人数和总人数的比值得出扇形的圆心角度数;(3)、首先根据题意画出树状图,然后根据概率的计算法则得出答案.
详解:(1)∵总人数为15÷15%=100(人),
∴D组人数m=100×30%=30,E组人数n=100×20%=20,
补全条形图如下:
(2)扇形统计图中“C组”所对应的圆心角的度数是360°×=90°,
(3)记通过为A、淘汰为B、待定为C,
画树状图如下:
由树状图可知,共有27种等可能结果,其中获得两位评委老师的“通过”有7种情况,
∴E组学生王云参加鄂州市“汉字听写”比赛的概率为.
点睛:本题主要考查的就是扇形统计图、条形统计图以及概率的计算法则,属于基础题型.解决这个问题,我们一定要明白样本容量=频数÷频率,根据这个公式即可进行求解.
22.(1)50,24 ; (2)72°; (3)160名
【解析】分析:(1)根据B级的人数和所占的百分比求出抽取的总人数,再用A级的人数除以总数即可求出a;
(2)用抽取的总人数减去A、B、D的人数,求出C级的人数,从而补全统计图;用360度乘以C级所占的百分比即可求出扇形统计图中C级对应的圆心角的度数;
(3)用D级所占的百分比乘以该校的总人数,即可得出该校D级的学生数.
详解:(1)在这次调查中,一共抽取的学生数是: =50(人),a=×100%=24%;
故答案为:50,24;
(2)等级为C的人数是:50﹣12﹣24﹣4=10(人),补图如下:
扇形统计图中C级对应的圆心角为×360°=72°;
故答案为:72;
(3)根据题意得:2000×=160(人).
答:该校D级学生有160人.
点睛:本题考查了是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
23.(1)本次抽样调查的学生总人数是200,a=30%,b=35%;(2)补图见解析;(3)全校选择“音乐舞蹈”社团的学生人数大约有420人.
【解析】分析:(1)美好“书法”社团有20人占10%求抽样调查的人数,分别用60,70除以调查的人数再乘以100%;(2)求出“国际象棋”社团的人数即可画条形图;(3)用“音乐舞蹈”社团的人数的百分比乘以全校学生人数.
详解:(1)本次抽样调查的学生总人数是:20÷10%=200,
a=×100%=30%,
b=×100%=35%.
(2)国际象棋的人数是:200×20%=40,
条形统计图补充如下:
(3)1200×35%=420人,
答:全校选择“音乐舞蹈”社团的学生人数大约有420人.
点睛:本题主要考查了条形统计图与用样本估计总体,从条形统计图和统计表格中获取有用的信息是解决这类问题的关键.
24.;补图见解析;全校男生中经常参加课外体育锻炼并且最喜欢的项目是篮球的人数约为人;这个说法不正确,理由见解析.
【解析】分析:(1)用“经常参加”所占的百分比乘以360°计算即可得解;
(2)先求出“经常参加”的人数,然后求出喜欢篮球的人数,再补全统计图即可;
(3)用总人数乘以喜欢篮球的学生所占的百分比计算即可得解;
(4)根据喜欢乒乓球的27人都是“经常参加”的学生,“偶尔参加”的学生中也会有喜欢乒乓球的考虑解答.
详解:(1)360°×(1﹣15%﹣45%)=360°×40%=144°;
故答案为:144°;
(2)“经常参加”的人数为:300×40%=120人,喜欢篮球的学生人数为:120﹣27﹣33﹣20=120﹣80=40人;
补全统计图如图所示;
(3)全校男生中经常参加课外体育锻炼并且最喜欢的项目是篮球的人数约为:1200×=160人;
(4)这个说法不正确.
理由如下:小明得到的108人是全校经常参加课外体育锻炼的男生中最喜欢的项目是乒乓球的人数,而全校偶尔参加课外体育锻炼的男生中也会有最喜欢乒乓球的,因此应多于108人.
点睛:本题考查的是条形统计图和扇形统计图的综合运用,读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
