人教版初中数学八年级下册第十八章《平行四边形》18.1平行四边形同步练习题(含答案)
文档属性
| 名称 | 人教版初中数学八年级下册第十八章《平行四边形》18.1平行四边形同步练习题(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 134.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-10 08:31:56 | ||
图片预览

文档简介
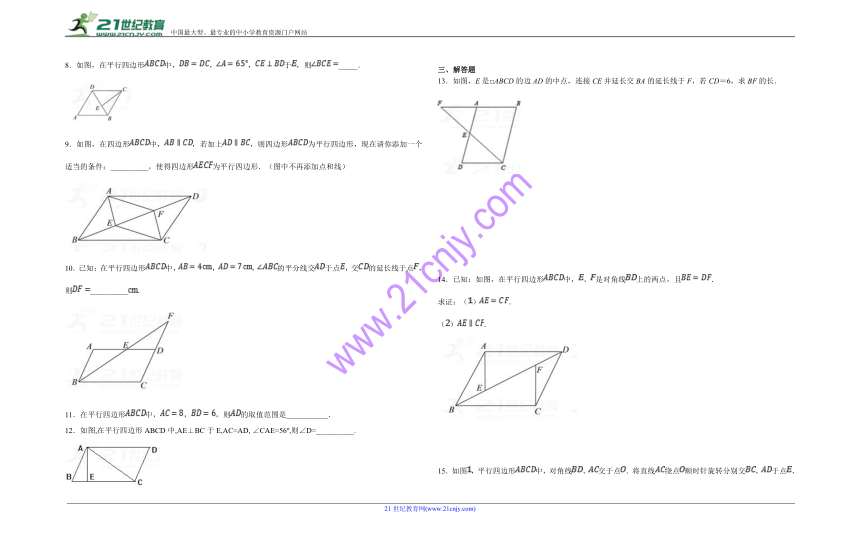
《18.1平行四边形》同步练习题
一、选择题(每小题只有一个正确答案)
1.已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )21教育网
A. OE=DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE21cnjy.com
2.如图,过平行四边形对角线交点的直线交于,交于,若,,,那么四边形周长是( ).21·cn·jy·com
A. B. C. D.
3.如图所示,在□ABCD中,E,F分别在BC,AD上,若想使四边形AFCE为平行四边形,须添加一个条件,这个条件可以是( )www.21-cn-jy.com
①AF=CF;②AE=CF;③∠BAE=∠FCD;④∠BEA=∠FCE。
A. ①或② B. ②或③ C. ③或④ D. ①或③或④
4.如图,四边形ABCD为平行四边形,蚂蚁甲沿A-B-C从A到C,蚂蚁乙沿B-C-D从B到D,两只蚂蚁速度相同且同时出发,则下列结论中,错误的是( )2·1·c·n·j·y
A. 甲到达B点时,乙也正好到达C点 B. 甲、乙同时到达终点
C. 甲、乙所经过的路程相同 D. 甲、乙所用的时间相同
5.如图,□ABCD中,BD=CD,∠C=70°,AE⊥BD于点E,则∠DAE=( )
A. 20° B. 25° C. 30° D. 35°
6.如图,四边形ABCD的对角线AC和BD交于点O,则下列不能判断四边形ABCD是平行四边形的条件是( )www-2-1-cnjy-com
A. OA=OC,AD∥BC B. ∠ABC=∠ADC,AD∥BC
C. AB=DC,AD=BC D. ∠ABD=∠ADB,∠BAO=∠DCO
7.如图,在?ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点,当E,F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )21*cnjy*com
A. AE=CF B. DE=BF C. ∠ADE=∠CBF D. ∠AED=∠CFB2-1-c-n-j-y
二、填空题
8.如图,在平行四边形中,,,于,则_____.
9.如图,在四边形中,,若加上,则四边形为平行四边形,现在请你添加一个适当的条件:__________,使得四边形为平行四边形.(图中不再添加点和线)21·世纪*教育网
10.已知:在平行四边形中,,,的平分线交于点,交的延长线于点,则__________.【来源:21cnj*y.co*m】
11.在平行四边形中,,,则的取值范围是___________.
12.如图,在平行四边形ABCD中,AE⊥BC于E,AC=AD, ∠CAE=56o,则∠D=__________. 【出处:21教育名师】
三、解答题
13.如图,E是□ABCD的边AD的中点,连接CE并延长交BA的延长线于F,若CD=6,求BF的长.21世纪教育网版权所有
14.已知:如图,在平行四边形中,、是对角线上的两点,且.
求证:().
().
15.如图,平行四边形中,对角线、交于点.将直线绕点顺时针旋转分别交、于点、.【来源:21·世纪·教育·网】
()在旋转过程中,线段与的数量关系是__________.
()如图,若,当旋转角至少为__________时,四边形是平行四边形,并证明此时的四边形是是平行四边形.21教育名师原创作品
16.如图,在□ABCD中,点E是AD的中点,BE的延长线与CD的延长线相交于点F。连结BD、AF.请判断四边形ABDF的形状,并说明你的理由.【版权所有:21教育】
参考答案
1.D2.C3.C4.A5.A6.D7.B
8.
9.
10.3
11.
12.73°
13.12
解析:
∵E是?ABCD的边AD的中点,
∴AE=DE,
∵四边形ABCD是平行四边形,
∴AB=CD=6,AB∥CD,
∴∠F=∠DCE,
在△AEF和△DEC中,
,
∴△AEF≌△DEC(AAS),
∴AF=CD=6,
∴BF=AB+AF=12.
14.
证明:()∵平行四边形
∴,
.
∴.
在和中,
∴≌,
∴
()∵≌,
∴
∴
∴.
15.()相等;()
解析:
()相等,理由如下:
如图所示:
在?ABCD中,AD∥BC,OA=OC, ∴∠1=∠2, 在△AOF和△COE中,
∴△AOF≌△COE(ASA), ∴AF=CE;
()证明:当旋转角为时,
,
又∵AB⊥AC, ∴∠BAO=90°, ∠AOF=90°, ∴∠BAO=∠AOF, ∴AB∥EF, ∵四边形ABCD是平行四边形, ∴AD∥BC, 即:AF∥BE, ∵AB∥EF,AF∥BE, ∴四边形ABEF是平行四边形;
16.四边形ABDF为平行四边形
【解析】四边形ABDF为平行四边形, 理由:如图所示:
∵四边形ABCD是平行四边形, ∴AB∥CD,AB=CD, ∴∠ABE=∠BFD, ∵点E是AD的中点, ∴AE=DE, ∵∠AEB=∠DEF, ∴△ABE≌△DFE, ∴AB=DF, ∵AB∥DF, ∴四边形ABDF为平行四边形.
一、选择题(每小题只有一个正确答案)
1.已知四边形ABCD是平行四边形,对角线AC、BD交于点O,E是BC的中点,以下说法错误的是( )21教育网
A. OE=DC B. OA=OC C. ∠BOE=∠OBA D. ∠OBE=∠OCE21cnjy.com
2.如图,过平行四边形对角线交点的直线交于,交于,若,,,那么四边形周长是( ).21·cn·jy·com
A. B. C. D.
3.如图所示,在□ABCD中,E,F分别在BC,AD上,若想使四边形AFCE为平行四边形,须添加一个条件,这个条件可以是( )www.21-cn-jy.com
①AF=CF;②AE=CF;③∠BAE=∠FCD;④∠BEA=∠FCE。
A. ①或② B. ②或③ C. ③或④ D. ①或③或④
4.如图,四边形ABCD为平行四边形,蚂蚁甲沿A-B-C从A到C,蚂蚁乙沿B-C-D从B到D,两只蚂蚁速度相同且同时出发,则下列结论中,错误的是( )2·1·c·n·j·y
A. 甲到达B点时,乙也正好到达C点 B. 甲、乙同时到达终点
C. 甲、乙所经过的路程相同 D. 甲、乙所用的时间相同
5.如图,□ABCD中,BD=CD,∠C=70°,AE⊥BD于点E,则∠DAE=( )
A. 20° B. 25° C. 30° D. 35°
6.如图,四边形ABCD的对角线AC和BD交于点O,则下列不能判断四边形ABCD是平行四边形的条件是( )www-2-1-cnjy-com
A. OA=OC,AD∥BC B. ∠ABC=∠ADC,AD∥BC
C. AB=DC,AD=BC D. ∠ABD=∠ADB,∠BAO=∠DCO
7.如图,在?ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点,当E,F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )21*cnjy*com
A. AE=CF B. DE=BF C. ∠ADE=∠CBF D. ∠AED=∠CFB2-1-c-n-j-y
二、填空题
8.如图,在平行四边形中,,,于,则_____.
9.如图,在四边形中,,若加上,则四边形为平行四边形,现在请你添加一个适当的条件:__________,使得四边形为平行四边形.(图中不再添加点和线)21·世纪*教育网
10.已知:在平行四边形中,,,的平分线交于点,交的延长线于点,则__________.【来源:21cnj*y.co*m】
11.在平行四边形中,,,则的取值范围是___________.
12.如图,在平行四边形ABCD中,AE⊥BC于E,AC=AD, ∠CAE=56o,则∠D=__________. 【出处:21教育名师】
三、解答题
13.如图,E是□ABCD的边AD的中点,连接CE并延长交BA的延长线于F,若CD=6,求BF的长.21世纪教育网版权所有
14.已知:如图,在平行四边形中,、是对角线上的两点,且.
求证:().
().
15.如图,平行四边形中,对角线、交于点.将直线绕点顺时针旋转分别交、于点、.【来源:21·世纪·教育·网】
()在旋转过程中,线段与的数量关系是__________.
()如图,若,当旋转角至少为__________时,四边形是平行四边形,并证明此时的四边形是是平行四边形.21教育名师原创作品
16.如图,在□ABCD中,点E是AD的中点,BE的延长线与CD的延长线相交于点F。连结BD、AF.请判断四边形ABDF的形状,并说明你的理由.【版权所有:21教育】
参考答案
1.D2.C3.C4.A5.A6.D7.B
8.
9.
10.3
11.
12.73°
13.12
解析:
∵E是?ABCD的边AD的中点,
∴AE=DE,
∵四边形ABCD是平行四边形,
∴AB=CD=6,AB∥CD,
∴∠F=∠DCE,
在△AEF和△DEC中,
,
∴△AEF≌△DEC(AAS),
∴AF=CD=6,
∴BF=AB+AF=12.
14.
证明:()∵平行四边形
∴,
.
∴.
在和中,
∴≌,
∴
()∵≌,
∴
∴
∴.
15.()相等;()
解析:
()相等,理由如下:
如图所示:
在?ABCD中,AD∥BC,OA=OC, ∴∠1=∠2, 在△AOF和△COE中,
∴△AOF≌△COE(ASA), ∴AF=CE;
()证明:当旋转角为时,
,
又∵AB⊥AC, ∴∠BAO=90°, ∠AOF=90°, ∴∠BAO=∠AOF, ∴AB∥EF, ∵四边形ABCD是平行四边形, ∴AD∥BC, 即:AF∥BE, ∵AB∥EF,AF∥BE, ∴四边形ABEF是平行四边形;
16.四边形ABDF为平行四边形
【解析】四边形ABDF为平行四边形, 理由:如图所示:
∵四边形ABCD是平行四边形, ∴AB∥CD,AB=CD, ∴∠ABE=∠BFD, ∵点E是AD的中点, ∴AE=DE, ∵∠AEB=∠DEF, ∴△ABE≌△DFE, ∴AB=DF, ∵AB∥DF, ∴四边形ABDF为平行四边形.
