16.2 用配方法推导一元二次方程的求根公式说课课件 (共29张PPT)
文档属性
| 名称 | 16.2 用配方法推导一元二次方程的求根公式说课课件 (共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-10 15:13:33 | ||
图片预览



文档简介
课件29张PPT。16.2 用配方法推导一元二次方程
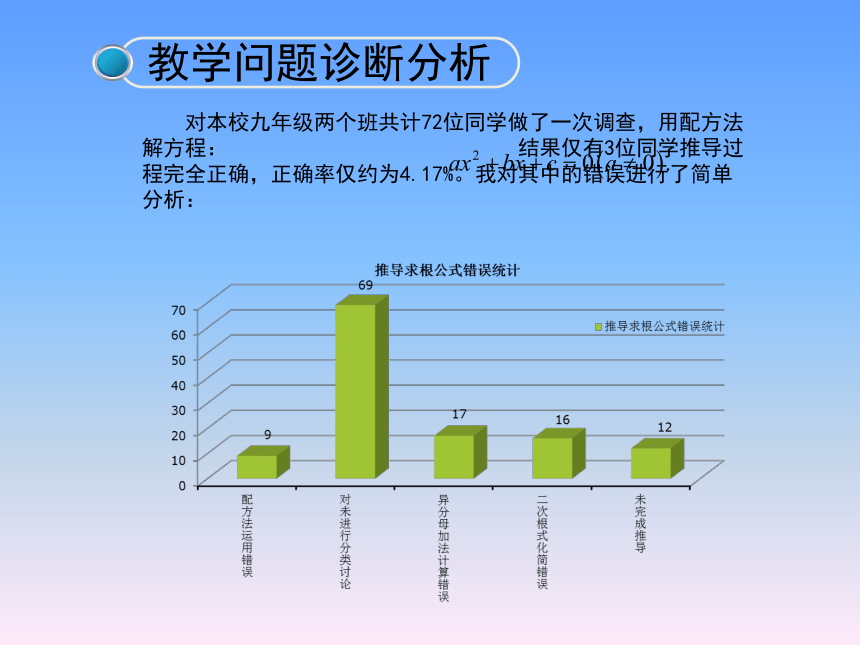
的求根公式教学重点教学难点 对本校九年级两个班共计72位同学做了一次调查,用配方法解方程: 结果仅有3位同学推导过程完全正确,正确率仅约为4.17%。我对其中的错误进行了简单分析:教学方式教学手段请每位同学编一道一元二次方程,每个小组从中选择一个,用配方法求解,填写以下表格.用配方法解一元二次方程 的步骤一元二次方程每组同学在以下方程中任选一个
用配方法求解.用配方法解方程: 由前面的探索我们发现,一元二次方程
(a≠0)的根是由方程未知数
的系数a、b、c决定的,由此我们得到了一元
二次方程的求根公式: 利用求根公式求一元二次方程的解的方法称为
公式法. 1.一元二次方程 的
求根公式:2.用求根公式解一元二次方程的步骤(流程图).是否用求根公式解一元二次方程的流程图1.每位同学在以下方程中任选一个用
配方法求解.2.阅读一元二次方程求根公式的历史.一元二次方程求根公式的历史 完全的一元二次方程 求根公式最早出现在公元前一千多年的古巴比伦文献中,在求不完全的一元二次方程 的求根公式时,发现了它的求根公式为 ,可悲的是当时世界上是清一色的不承认负根,自然不知道有两个根,只取一个正根并且二次项系数为1.
? 希腊数学家海伦,曾“独具慧眼”的得到方程 一个求根公式是 ,众所周知此公式是错误的,其错误原因是当时希腊人既不承认负数,又没有发现复数,其错误可以理解,“智者千虑,必有一失”.我国公元3世纪数学家赵爽著《周髀算经》里既发现又应用了形如 的求根公式 .
的求根公式教学重点教学难点 对本校九年级两个班共计72位同学做了一次调查,用配方法解方程: 结果仅有3位同学推导过程完全正确,正确率仅约为4.17%。我对其中的错误进行了简单分析:教学方式教学手段请每位同学编一道一元二次方程,每个小组从中选择一个,用配方法求解,填写以下表格.用配方法解一元二次方程 的步骤一元二次方程每组同学在以下方程中任选一个
用配方法求解.用配方法解方程: 由前面的探索我们发现,一元二次方程
(a≠0)的根是由方程未知数
的系数a、b、c决定的,由此我们得到了一元
二次方程的求根公式: 利用求根公式求一元二次方程的解的方法称为
公式法. 1.一元二次方程 的
求根公式:2.用求根公式解一元二次方程的步骤(流程图).是否用求根公式解一元二次方程的流程图1.每位同学在以下方程中任选一个用
配方法求解.2.阅读一元二次方程求根公式的历史.一元二次方程求根公式的历史 完全的一元二次方程 求根公式最早出现在公元前一千多年的古巴比伦文献中,在求不完全的一元二次方程 的求根公式时,发现了它的求根公式为 ,可悲的是当时世界上是清一色的不承认负根,自然不知道有两个根,只取一个正根并且二次项系数为1.
? 希腊数学家海伦,曾“独具慧眼”的得到方程 一个求根公式是 ,众所周知此公式是错误的,其错误原因是当时希腊人既不承认负数,又没有发现复数,其错误可以理解,“智者千虑,必有一失”.我国公元3世纪数学家赵爽著《周髀算经》里既发现又应用了形如 的求根公式 .
同课章节目录
