2018高考数学(理)名师押题冲刺高考最后一个月专题03+线性规划与三角函数
文档属性
| 名称 | 2018高考数学(理)名师押题冲刺高考最后一个月专题03+线性规划与三角函数 |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-10 12:53:38 | ||
图片预览




文档简介
一.线性规划小题
(一)命题特点和预测:分析近7年的高考试题发现,线性规划7年6考,每年1题,主要考查利用数形结合思想解简单的线性规划问题,是基础题,少数年份考线性规划应用题、斜率型规划问题和规划问题与其他知识的交汇,难度较大.2018年仍将重点考查目标函数为线性的规划问题,也可能考查含参数的线性规划问题、目标函数为斜率型和距离型的规划问题、线性规划应用题及规划与简易逻辑、几何概型的交汇问题,要做好这方面问题的复习和训练.
(二)历年试题比较:
年份
题目
答案
2017年
(14)设x,y满足约束条件则的最小值为 .
2016年
(16)某高科技企业生产产品A和产品B需要甲、乙两种新型材料。生产一件产品A需要甲材料1.5kg,乙材料1kg,用5个工时;生产一件产品B需要甲材料0.5kg,乙材料0.3kg,用3个工时,生产一件产品A的利润为2100元,生产一件产品B的利润为900元。该企业现有甲材料150kg,乙材料90kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为 元.
216000
2015年
(15)若满足约束条件,则的最大值为 .
4
2014年
(9)不等式组的解集为D,有下面四个命题:
, ,
?????,
其中的真命题是( )
A.????B.?????C.???D.
B
2012年
(14)设,满足约束条件,则的取值范围为 .
2011年
(13)若变量,满足约束条件,则的最小值为 .
-6
【解析与点睛】
【名师点睛】本题是常规的线性规划问题,线性规划问题常出现的形式有:①直线型,转化成斜截式比较截距,要注意前面的系数为负时,截距越大,值越小;②分式型,其几何意义是已知点与未知点的斜率;③平方型,其几何意义是距离,尤其要注意的是最终结果应该是距离的平方;④绝对值型,转化后其几何意义是点到直线的距离.
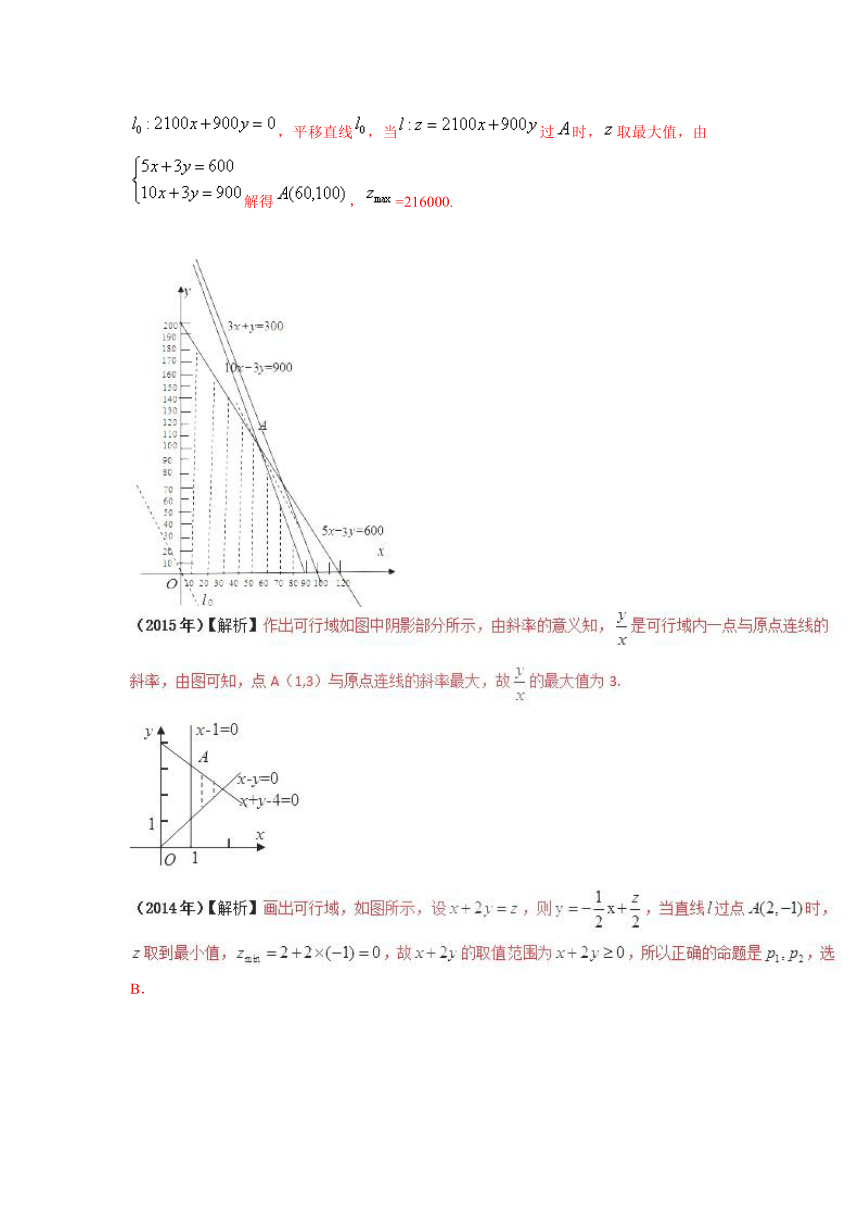
(2016年)【解析】设分别生产件产品,则,即,目标函数为,作出可行域如图所示,作出直线,平移直线,当过时,取最大值,由解得,=216000.
B.
(2012年)【解析】作出可行域如图中阴影部分所示,作出直线:=0,平移直线,有图像知,
(三)命题专家押题
题号
试 题
1.
设满足约束条件,则目标函数取最小值时的最优解是( )
A. ????B. ????C. ????D.
2.
若实数,?满足,则的最小值( )
A. 1 B. 3 C. 4 D. 9
3
已知点,点满足,则在方向上的投影的最大值是__________.
4
已知实数,满足不等式组,则的取值范围为( )
A. B. C. D.
5
已知实数,?满足条件则的最大值为__________.
6
若目标函数在约束条件下当且仅当在点处取得最小值,则实数的取值范围是 .?
7
已知实数满足如果目标函数的最大值为,则实数
A. ????B. ????C. ????D.
8
一个化肥厂生产甲、乙两种混合肥料,生产1车皮甲种肥料的主要原料是磷酸盐4吨,硝酸盐18吨;生产1车皮乙种肥料需要的主要原料是磷酸盐1吨,硝酸盐15吨.现库存磷酸盐10吨,硝酸盐66吨,在此基础上生产这两种混合肥料.如果生产1车皮甲种肥料产生的利润为12 000元,生产1车皮乙种肥料产生的利润为7 000元,那么可产生的最大利润是( )
A. 29 000元 B. 31 000元 C. 38 000元 D. 45 000元
9
已知实数满足约束条件,则的取值范围是__________.
10
若实数,满足不等式组,则的最小值是__________.
【详细解析】
1.【答案】B
2.【答案】B
4.【答案】C
5.【答案】
【解析】由约束条件画出可行域,如下图,目标函数为点(x,y)与点(-3,0)两点连线的斜率。
由图可知斜率最大值时过B(1,2)点斜率为,填。
6.【答案】
7.【答案】B
【解析】由题得不等式组对应的可行域如图所示:
由目标函数得,当直线经过点A时,直线的纵截距最大,z最大.联立方程所以2+2-m=0,所以m=4. 故选B.
8.【答案】C
【解析】设分别表示计划生产甲、乙两种肥料的车皮数,根据题意得
点到点的距离最大,故;
点到直线的距离最小,即,
所以的取值范围是.
10.【答案】
【解析】画出不等式组表示的可行域如图阴影部分所示.
二.三角函数小题
(一)命题特点和预测:分析近7年的高考题发现,7年13考,每年至少1题,多数年份是2小、3小,个别年份4小,主要考查三角函数定义、诱导公式、同角三角函数基本关系、和差倍半公式、图象变换、三角函数的图象与性质、利用正余弦定理解三角形,难度一般为1个基础题、2个中档题、有时也会为压轴题.2018年高考仍将坚持至少1小、难度为1基础1(或2)中档、重点考查三角公式、图象变换、三角函数图象与性质、正余弦定理应用,可能在与其他知识交汇处命题,适度创新.
(二)历年试题比较:
年份
题目
答案
2017年
(9)已知曲线,则下面结论正确的是
A.把上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线
B.把上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线
C.把上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向右平移个单位长度,得到曲线
D.把上各点的横坐标缩短到原来的倍,纵坐标不变,再把得到的曲线向左平移个单位长度,得到曲线
D
2016年
(12)已知函数为的零点,为图像的对称轴,且在单调,则的最大值为( )
(A)11 (B)9 (C)7 (D)5
B
2015年
(2)?=( ????)
?(A)????????(B)?????(C)?????(D)
D
(8)函数=的部分图像如图所示,则的单调递减区间为( )
(A)???(B)
(C)?????(D)?
D
(16)在平面四边形ABCD中,∠A=∠B=∠C=75°,BC=2,则AB的取值范围是 .
,
2014年
(6)如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角的始边为射线,终边为射线,过点作直线的垂线,垂足为,将点到直线的距离表示为的函数,则=在[0,]上的图像大致为
C
(8)设且则( )
?(A)???(B)??(C)??(D)
C
(16)已知分别为三个内角的对边,,且,则面积的最大值为____________.
2013年
(15)设当x=θ时,函数f(x)=sin x-2cos x取得最大值,则cos θ=__________.
2012年
(9)已知>0,函数=在(,)单调递减,则的取值范围是( )
.[,] ???.[,] ???.(0, ] ????.(0,2]
A
2011年
(5)已知角θ的顶点与原点重合,始边与x轴的正半轴重合,终边在直线y=2x上,则cos2θ=( )
A.- B.- C. D.
B
(11)设函数=(>0,<)的最小正周期为,且=,则
(A)在(0,)单调递减 (B)在(,)单调递减
(C) 在(0,)单调递增 (D)在(,)单调递增
A
(16)在△ABC中,B=60°,AC=,则AB+2BC的最大值为__________.
【解析与点睛】
(2017年)【解析】因为函数名不同,所以先将利用诱导公式转化成与相同的函数名,则,则由上各点的横坐标缩短到原来的倍变为,再将曲线向左平移个单位长度得到,故选D.
【名师点睛】对于三角函数图象变换问题,首先要将不同名函数转换成同名函数,利用诱导公式,需要重点记住;另外,在进行图象变换时,提倡先平移后伸缩,而先伸缩后平移在考试中也经常出现,无论哪种变换,记住每一个变换总是对变量而言.
(2016年)【解析】当时,由,,∴,因为,所以,所以=,当时,,因为在不单调,故A错;当时,由,,∴,因为,所以,所以=,当时,,因为在单调,故选B.
(2015年)(2)【解析】原式= ==,故选D.
(16)【解析】如图所示,延长BA, CD交于E,平移AD,当A与D重合与E点时,AB最长,在△BCE中,∠B=∠C=75°,∠E=30°,BC=2,由正弦定理可得,即,解得=,平移AD ,当D与C重合时,AB最短,此时与AB交于F,在△BCF中,∠B=∠BFC=75°,∠FCB=30°,由正弦定理知,,即,解得BF=,所以AB的取值范围为(,).
(2014年)(4)【解析】如图所示,当时,在中,.在中,;当时,在中,,在中,,所以当时,的图象大致为C.
(8)【解析】由已知得,,去分母得,,=sin(α+x),当x=2kπ+-α(k∈Z)时,sin(α+x)有最大值1,f(x)有最大值,即θ=2kπ+-α(k∈Z),所以cos θ===sin α=.
则有AB+2BC
(三)命题专家押题
题号
试 题
1.
若,则的值为( )
A. B. C. D.
2.
已知角α的顶点与原点O重合,始边与x轴的正半轴重合,若它的终边经过点,则
A. -7 B. ????C. ????D. 7
3
在中,角所对应的边分别是,若
,则角等于
A. ????B. ????C. ????D.
4
的三个内角,?,?的对边分别为,?,?,若,?,则的取值范围是( )
A. ????B. ????C. ????D.
5
函数的部分图像如图所示,则关于函数的下列说法正确的是( )
A. 图像关于点中心对称 B. 图像关于直线对称
C. 图像可由的图像向左平移个单位长度得到 D. 在区间上单调递减
6
将函数的图象向左平移个单位长度后,所得图象关于轴对称,则函数在上的最小值为( )
A. B. C. D.
7
已知函数,若,?的图象恒在直线的上方,则的取值范围是( )
A. ????B. ????C. ????D.
8
若将函数f(x)=sin(2x+φ)+cos(2x+φ)(0<φ<π)的图象向左平移个单位长度,平移后的图象关于点对称,则函数g(x)=cos(x+φ)在上的最小值是
A. -????B. -????C. ????D.
9
在中,角的对边分别为,设的面积为,若,则的最大值为___________.
10
已知点在内部,?平分,?,对满足上述条件的所有,下列说法正确的是( ??)
的三边长一定成等差数列 ????????????????
B. 的三边长一定成等比数列
C. ,?,?的面积一定成等差数列
D. ,?,?的面积一定成等比数列
【详细解析】
3.【答案】D
【解析】∵,∴(a﹣b)(a+b)=c(c+b),∴a2﹣c2﹣b2=bc,由余弦定理可得cosA=∵A是三角形内角,∴A=故选D.
4.【答案】D
【解析】由cosAcosBcosC>0,可知,三角形是锐角三角形,由题意有sinB=sin2A=2sinAcosA,结合正弦定理有b=2acosA, ,∵A+B+C=180°,B=2A,∴3A+C=180°, ,∵2A<90°,∴, ,即的取值范围是,故选D.
7.【答案】C
【解析】的图象恒在直线的上方,即恒成立,
当k=0时, 的取值范围是.
8.【答案】D
【解析】,将函数向左平移个单位后,得到函数解析式为:,图象关于点对称,则对称中心在函数图象上,可得:,解得, ,, ,,, ,,则函数在上的最小值为,故选
9.【答案】
,①
,②
.③
由①+②整理得,
同课章节目录
