2018高考数学(文)名师押题冲刺高考最后一个月专题03+线性规划与三角函数
文档属性
| 名称 | 2018高考数学(文)名师押题冲刺高考最后一个月专题03+线性规划与三角函数 |  | |
| 格式 | zip | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-10 12:54:25 | ||
图片预览




文档简介
一.线性规划小题
(一)命题特点和预测:分析近7年的高考试题发现,线性规划7年7考,每年1题,主要考查利用数形结合思想解简单的线性规划问题,是基础题,少数年份考线性规划应用题和含参数得线性规划问题,难度较大.2018年仍将重点考查目标函数为线性的规划问题,也可能考查含参数的线性规划问题和线性规划应用题,要做好这方面问题的复习和训练.
(二)历年试题比较:
年份
题目
答案
2017年
(7)设x,y满足约束条件则z=x+y的最大值为
A.0 B.1 C.2 D.3
D
2016年
(16)某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5 kg,乙材料1 kg,用5个工时;生产一件产品B需要甲材料0.5 kg,乙材料0.3 kg,用3个工时,生产一件产品A的利润为2100元,生产一件产品B的利润为900元。该企业现有甲材料150 kg,乙材料90 kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为 元.
2015年
(15)若x,y满足约束条件?,则z=3x+y的最大值为 .
4
2014年
(11)设,满足约束条件,且的最小值为7,则
A.-5 B.3 C.-5或3 D.5或-3
B
2013年
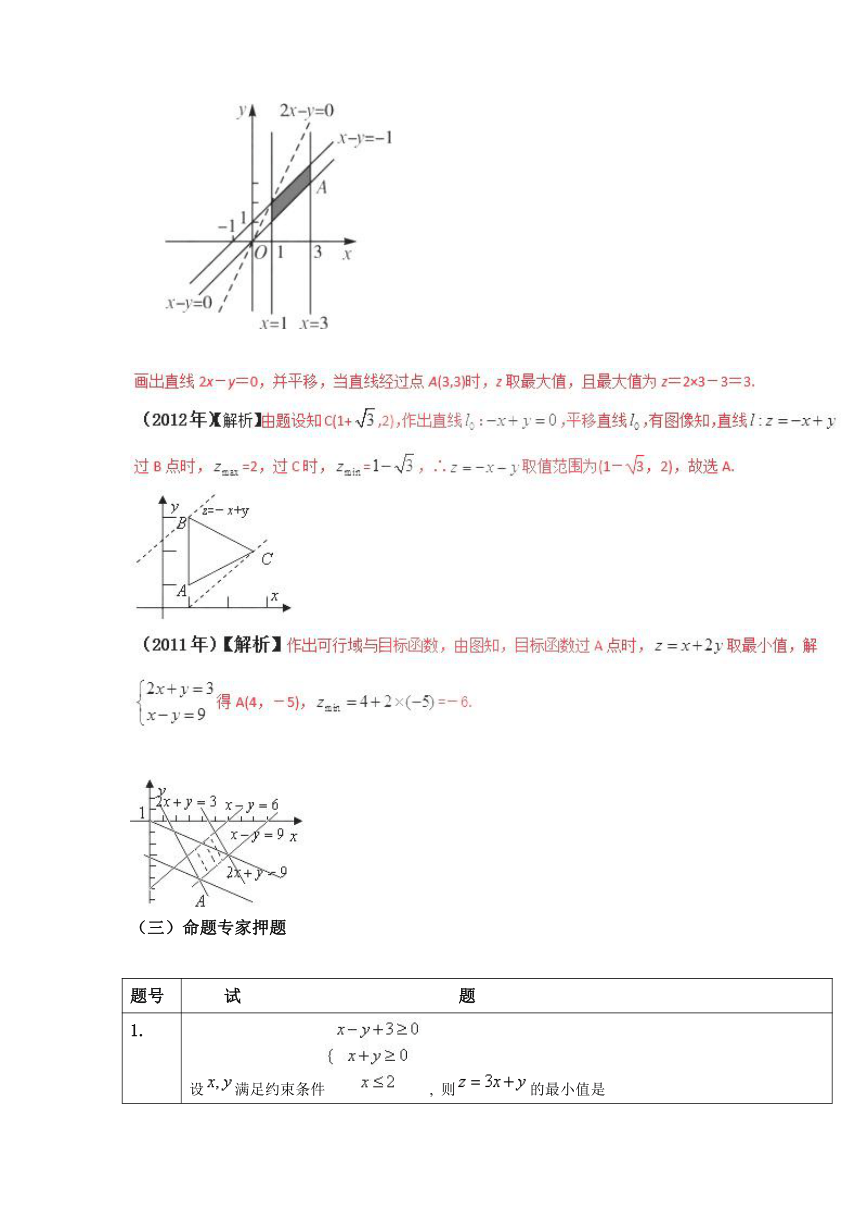
(14)设x,y满足约束条件则z=2x-y的最大值为______.
3
2012年
(5)已知正三角形ABC的顶点A(1,1),B(1,3),顶点C在第一象限,若点(x,y)在△ABC内部,则的取值范围是
(A)(1-,2) (B)(0,2)
(C)(-1,2) (D)(0,1+)
2011年
(14)若变量满足约束条件,则的最小值为 .
-6
【解析与点睛】
【名师点睛】本题主要考查线性规划问题,首先由不等式组作出相应的可行域,并明确可行域对应的是封闭区域还是开放区域、分界线是实线还是虚线,其次确定目标函数的几何意义,是求直线的截距、两点间距离的平方、直线的斜率、还是点到直线的距离等等,最后结合图形确定目标函数的最值取法或值域范围.
(2016年)【解析】设生产产品A、产品B分别为、件,利润之和为元,那么由题意得约束条件即 目标函数.
作出二元一次不等式组①表示的平面区域,即可行域,如图中阴影部分所示.
将变形,得,作直线:并平移,当直线经过点时, 取得最大值.
解方程组,得的坐标为.
所以当,时,.
故生产产品A、产品B的利润之和的最大值为元.
(2013年)【解析】画出可行域如图所示.
(三)命题专家押题
题号
试 题
1.
设满足约束条件, 则的最小值是
A. ????B. ????C. ????D.
2.
设,满足,则的取值范围为__________.
3
若实数,?满足约束条件,则的最小值为( )
A. ????B. 2 ???C. ????D. 4
4
已知点,点的坐标满足条件,则的最小值是( )
A. B. C. 1 D.
5
已知、满足约束条件则目标函数的最小值为( )
A. ????B. ????C. ????D.
6
设满足约束条件,则的最大值为( )
A. 1 B. ????C. ????D.
7
已知满足不等式组则的最小值为( )
A. 2 B. ????C. ????D. 1
8
某农户计划种植黄瓜和韭菜,种植面积不超过50亩,投入资金不超过54万元,假设种植黄瓜和韭菜的产量、成本和售价如下表:
为使一年的种植总利润(总利润=总销售收入-总种植成本)最大,那么黄瓜和韭菜的种植面积(单位:亩)分别为( )
A. 50,0 B. 30,20 C. 20,30 D. 0,50
9
已知变量满足,目标函数的最小值为5,则的值为__________.
10
已知是不等式组表示平面区域内任意一点,是坐标原点,(2,1),则的最大值为________.
【详细解析】
1.【答案】C
2.【答案】
【解析】由题意,先作出约束条件的可行域图形,如图中阴影部分,将目标函数转化为,在图中作出平行直线,在可行域范围内平行移动直线,则当移到顶点处时,有,由于可行域向上无限延展,所以目标函数的取值范围为.
3.【答案】B
4.【答案】B
【解析】作出平面区域如图所示:
由图可知最小值为点到直线的距离,为.故选B.
5.【答案】B
6.【答案】B
【解析】画出可行域如图所示:
联立,解得,则.,表示可行域内的点与连线的斜率,从图像可以看出,经过点时, 有最大值,故选B.
7.【答案】D
【解析】不等式组对应的可行域如图所示,
因为所以z表示可行域内一点到直线x+y-1=0距离的倍,由可行域可知点A(2,0)到直线x+y-1=0的距离最短,故故选D.
5,此时 ,解得坐标为,代入得.
二.三角函数小题
(一)命题特点和预测:分析近7年的高考题发现,7年17考,每年至少1题,多数年份是2小、3小,个别年份4小,主要考查三角函数定义、诱导公式、同角三角函数基本关系、和差倍半公式、图象变换、三角函数的图象与性质、利用正余弦定理解三角形,难度一般为1个基础题、2个中档题、有时也会为难题.2018年高考仍将坚持至少1小、难度为1基础1(或2)中档、重点考查三角公式、图象变换、三角函数图象与性质、正余弦定理应用,可能在与其他知识交汇处命题,适度创新.
(二)历年试题比较:
年份
题目
答案
2017年
(11)△ABC的内角A、B、C的对边分别为a、b、c。已知,a=2,c=,则C=
A. B. C. D.
B
(15)已知,tan α=2,则=__________。
2016年
(4)△ABC的内角A、B、C的对边分别为a、b、c.已知,,,则b=
(A)?????????(B)?????????(C)2 (D)3
D
(6)将函数y=2sin (2x+)的图像向右平移个周期后,所得图像对应的函数为
(A)y=2sin(2x+) ?(B)y=2sin(2x+) ?(C)y=2sin(2x–) ?(D)y=2sin(2x–)
D
(12)若函数在单调递增,则a的取值范围是
(A)(B)(C)(D)
C
(14)已知θ是第四象限角,且sin(θ+)=,则tan(θ–)= .
2015年
(8)函数的部分图像如图所示,则的单调递减区间为( )
(A)?
(B)
(C)
(D)
D
2014年
(2)若,则
????????B. ????C. ????????D.
A
(7)在函数①,②?,③,④中,最小正周期为的所有函数为
A. ②④????B. ①③④??????C. ①②③?????????D. ①③
C
(16)如图,为测量山高,选择和另一座山的山顶为测量观测点.从点测得 点的仰角,点的仰角以及;从点测得.已知山高,则山高________.
150
2013年
(9)函数=在的图像大致为
C
(10)?已知锐角△ABC的内角A,B,C的对边分别为,,,,=7,,则=
.10 ??.9 ???.8 ???.5
D
(16)设当=时,函数=取得最大值,则=______.
2012年
(9)已知>0,,直线=和=是函数图像的两条相邻的对称轴,则=
(A)???????(B)??????(C)??????(D)
A
2011年
(7)已知角的顶点与原点重合,始边与轴的正半轴重合,终边在直线上,则=
(A)????(B)???(C) ??(D)
B
( 11).设函数=,则=
(A)在(0,)单调递增,其图像关于直线=对称
(B) 在(0,)单调递增,其图像关于直线=对称
(C) 在(0,)单调递减,其图像关于直线=对称?
(D) 在(0,)单调递减,其图像关于直线=对称
D
(15)中,,AC=7,AB=5,则的面积为 .
【解析与点睛】
个单位,所得图象对应的函数为=,故选D.
(12)【解析】=对恒成立,故,即恒成立,即对恒成立;设=(),所以,解得,故选C.
(14)【解析】由题意, 解得
所以,
(2013年)(9)【解析】显然是奇函数,故排除B,当时,<0,故排除A,∵==,由≥0解得,又∵,∴,同理,由≤0解得,或,
∴在[-,-]上是减函数,在[-,]上是增函数,在[,]上是减函数,
∴当=时,取最小值=,最小值点靠近-,故选.
(10)【解析】由及△ABC是锐角三角形得=,∵=7,,∴,即,解得或=(舍),故选.
(16)【解析】∵==,令=,
(15)【解析】由余弦定理得,=,即
=,即,解得=3或=-8(舍),
===.
(三)命题专家押题
题号
试 题
1.
若,则( )
A. B. C. D.
2.
函数的部分图像如图所示,则关于函数的下列说法正确的是( )
A. 图像关于点中心对称 B. 图像关于直线对称
C. 图像可由的图像向左平移个单位长度得到 D. 在区间上单调递减
3
将函数的图象向右平移个单位,得到函数的图象,若函数在上单调递增,则的值不可能为( )
A. B. C. D.
4
将函数的图象向左平移个单位后的图象关于原点对称,则函数在上的最小值为( )
A. ????B. ????C. ????D.
5
知角α的顶点与原点O重合,始边与x轴的正半轴重合,若它的终边经过点,则
A. -7 B. ????C. ????D. 7
6
如图,为测量一座山的高度,某勘测队在水平方向的观察点,?测得山顶的仰角分别为,?,且该两点间的距离是米,则此山的竖直高度为__________米(用含,?,?的式子表达).
7
已知函数的图象关于点对称.且在区间上单调,则的值为( )
A. 2 B. ????C. ????D.
8
在中,若,则的取值范围为( )
A. B. C. D.
9
我国南宋著名数学家秦九韶在他的著作《数书九章》卷五“田域类”里有一个题目:“问有沙田一段,有三斜,其小斜一十三里,中斜一十四里,大斜一十五里.里法三百步.欲知为田几何.”这道题讲的是有一个三角形沙田,三边分别为里,?里,?里,假设里按米计算,则该三角形沙田外接圆的半径为___________米.
10
已知锐角的内角的对边分别为,且,则的最大值为__________.
【详细解析】
1.【答案】C
3.【答案】C
【解析】将函数的图象向右平移个单位,得到函数的图象,当时,,若时,,即函数在, , ,故选A.
6.【答案】
【解析】如图在中有,则.
在中, ,则,故高度: .
9.【答案】
【解析】由题意画出图象,如上图所示,且里=6500米, 里=7000米, 里=7500米,在中,由余弦定理有,B为锐角, ,设外接圆半径为,则由正弦定理有, 米。
10.【答案】
【解析】 由题意,根据正弦定理化简得,
又由,则,
同课章节目录
