高三第一轮复习教学课件[上下学期通用]
图片预览


文档简介
课件14张PPT。。
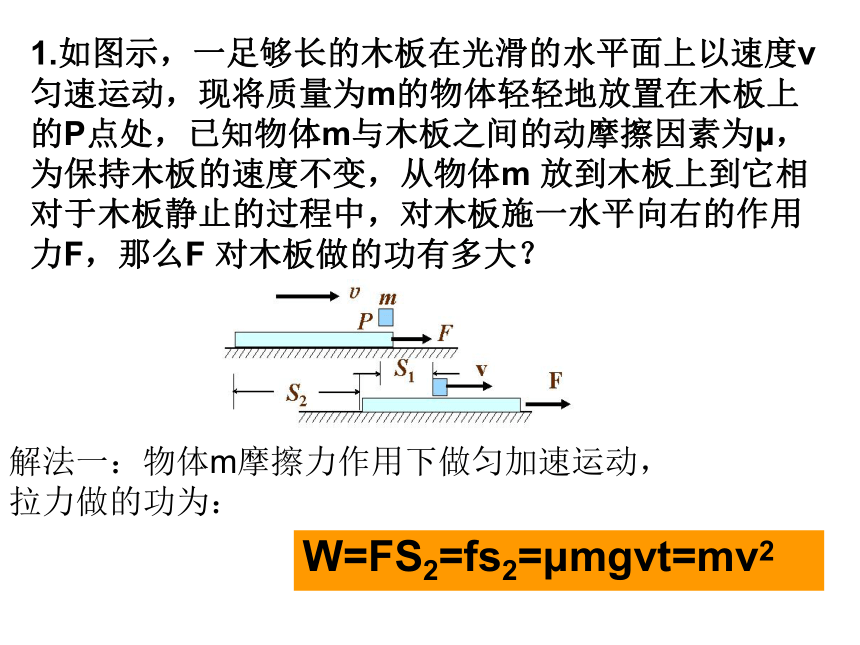
10. 1.图中,轻弹簧的一端固定,另一端与滑块B相连,B静止在水平直导轨上,弹簧处在原长状态。另一质量与B相同的滑块A,从导轨上的P点以某一初速度向B滑行。当A滑过距离时,与B相碰,碰撞时间极短,碰后A、B紧贴在一起运动,但互不粘连。已知最后A恰好返回到出发点P并停止。滑块A和B与导轨的滑动摩擦因数都为μ,运动过程中弹簧最大形变量为,重力加速度为。求A从P点出发时的初速度。 L1L21.如图示,一足够长的木板在光滑的水平面上以速度v匀速运动,现将质量为m的物体轻轻地放置在木板上的P点处,已知物体m与木板之间的动摩擦因素为μ,为保持木板的速度不变,从物体m 放到木板上到它相对于木板静止的过程中,对木板施一水平向右的作用力F,那么F 对木板做的功有多大? W=FS2=fs2=μmgvt=mv2解法一:物体m摩擦力作用下做匀加速运动,拉力做的功为: 解法二:由能量守恒定律,拉力F 的功等于物体动能的增加和转化的内能.
W=1/2×mv2+fΔs= 1/2×mv2+f(s2-s1)
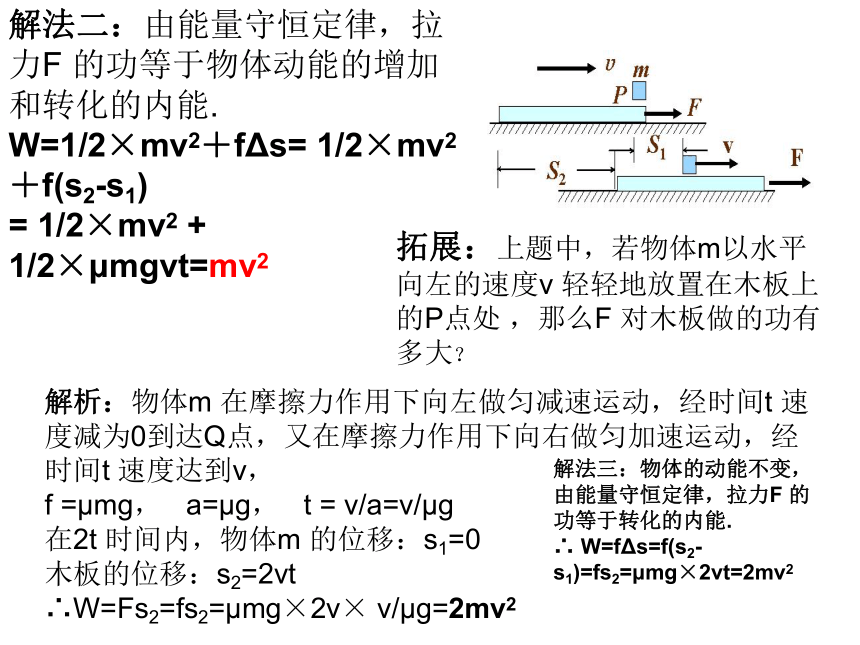
= 1/2×mv2 + 1/2×μmgvt=mv2拓展:上题中,若物体m以水平向左的速度v 轻轻地放置在木板上的P点处 ,那么F 对木板做的功有多大?解析:物体m 在摩擦力作用下向左做匀减速运动,经时间t 速度减为0到达Q点,又在摩擦力作用下向右做匀加速运动,经时间t 速度达到v,
f =μmg, a=μg, t = v/a=v/μg
在2t 时间内,物体m 的位移:s1=0
木板的位移:s2=2vt
∴W=Fs2=fs2=μmg×2v× v/μg=2mv2解法三:物体的动能不变,由能量守恒定律,拉力F 的功等于转化的内能.
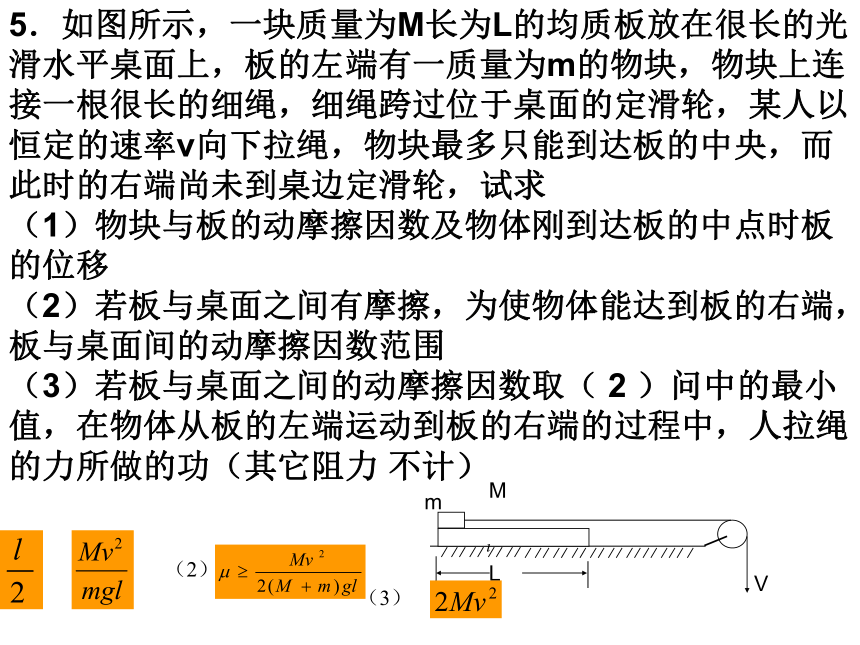
∴ W=fΔs=f(s2-s1)=fs2=μmg×2vt=2mv2 领悟: ①隔离分析m的时候,参考系是地面而不是木板,所以木板对物体的摩擦力产生的加速度是物体相对于地面的加速度!故分析m的运动时也应该以地面为参考系.②能量观点解题可以使解答过程变得十分简练!所以,通常应该优先考虑能量观点求解! L mMV5.如图所示,一块质量为M长为L的均质板放在很长的光滑水平桌面上,板的左端有一质量为m的物块,物块上连接一根很长的细绳,细绳跨过位于桌面的定滑轮,某人以恒定的速率v向下拉绳,物块最多只能到达板的中央,而此时的右端尚未到桌边定滑轮,试求
(1)物块与板的动摩擦因数及物体刚到达板的中点时板的位移
(2)若板与桌面之间有摩擦,为使物体能达到板的右端,板与桌面间的动摩擦因数范围
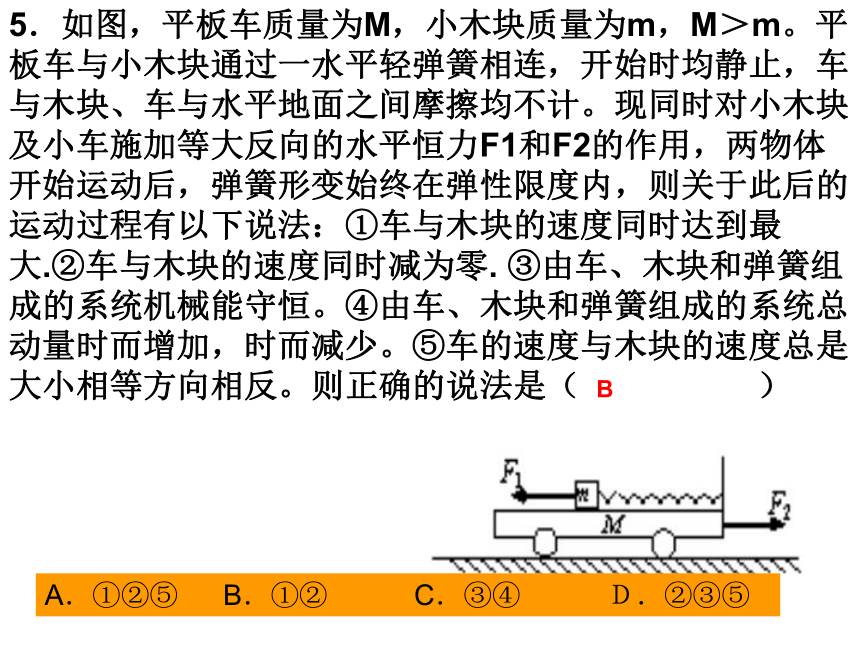
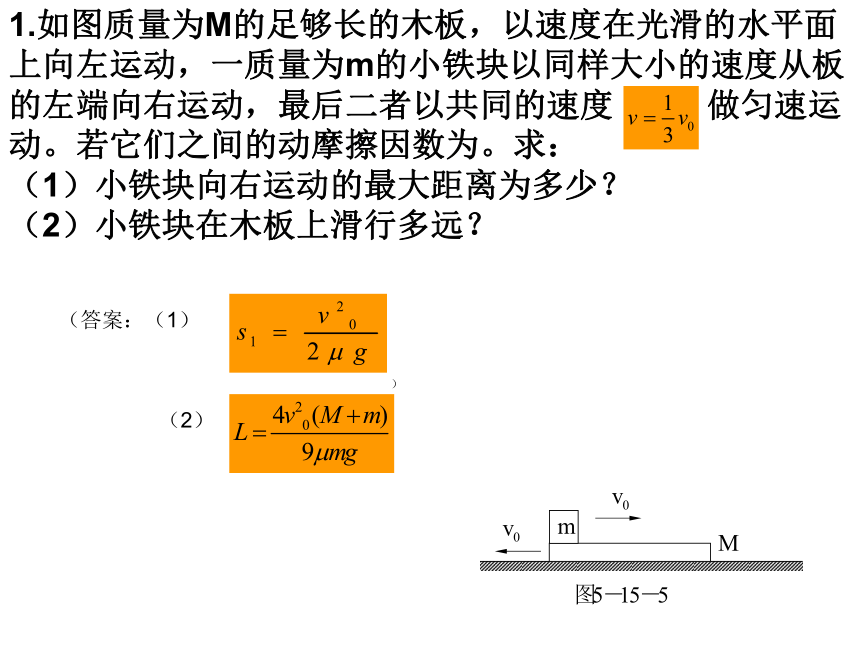
(3)若板与桌面之间的动摩擦因数取( 2 )问中的最小值,在物体从板的左端运动到板的右端的过程中,人拉绳的力所做的功(其它阻力 不计) (2) (3)5.如图,平板车质量为M,小木块质量为m,M>m。平板车与小木块通过一水平轻弹簧相连,开始时均静止,车与木块、车与水平地面之间摩擦均不计。现同时对小木块及小车施加等大反向的水平恒力F1和F2的作用,两物体开始运动后,弹簧形变始终在弹性限度内,则关于此后的运动过程有以下说法:①车与木块的速度同时达到最大.②车与木块的速度同时减为零. ③由车、木块和弹簧组成的系统机械能守恒。④由车、木块和弹簧组成的系统总动量时而增加,时而减少。⑤车的速度与木块的速度总是大小相等方向相反。则正确的说法是( )A.①②⑤ B.①② C.③④ D.②③⑤ B1.如图质量为M的足够长的木板,以速度在光滑的水平面上向左运动,一质量为m的小铁块以同样大小的速度从板的左端向右运动,最后二者以共同的速度 做匀速运动。若它们之间的动摩擦因数为。求:
(1)小铁块向右运动的最大距离为多少?
(2)小铁块在木板上滑行多远?(答案:(1)(2)) 3.如图所示,一质量为M,长为l的长方形木板B放在光滑的水平面上,其右端放一质量为m的小物体A(m<M)。现以地面为参照系,给A和B以大小相等,方向相反的初速度使A开始向左运动,B开始向右运动,但最后A刚好没有滑离B板。(1)若已知A和B的初速度大小为v0,求它们最后的速度大小和方向;(2)若初速度的大小未知,求小木块A向左运动到达最远处(从地面上看)离出发点的距离。LB , , 2. 如图所示,A、B是静止在水平地面上完全相同的两块长木板。A的左端和B的右端相接触。两板的质量皆为M=2.0kg,长度=1.0m。C是一质量为m=1.0kg的小物块。现给它一初速度=2.0m/s,使它从B板的左端开始向右滑动。已知地面是光滑的,而C与A、B之间的动摩擦因数皆为=0.10。求最后A、B、C各以多大的速度做匀速运动(重力加速度g取10)13.如图,长木板ab的b端固定一挡板,木板连同挡板的质量为=4.0kg,a、b间距离s=2.0m。木板位于光滑水平面上。在木板a端有一小物块,其质量m=1.0kg,小物块与木板间的动摩擦因数=0.10,它们都处于静止状态。现令小物块以初速=4.0m/s沿木板向前滑动,直到和挡板相碰。碰撞后,小物块恰好回到a端而不脱离木板。求碰撞过程中损失的机械能。2.4J 子弹打木块模型例? 如图3-6,质量为M的木块放在光滑水平面上,现有一质量为m的子弹以速度v0射入木块中。设子弹在木块中所受阻力不变,大小为f,且子弹未射穿木块。若子弹射入木块的深度为D,则木块向前移动距离是多少?系统损失的机械能是多少?例1.一轻质弹簧两端各连接一块质量为m的滑块A和B,A、B静置于光滑水平面上,质量为m/4的子弹以水平速度v0射入A中不再穿出,如图-9所示,求滑块B所获得的最大动能。解析:子弹打入A是个瞬间过程,弹簧还没有来得及被压缩,该过程满足动量守恒。然后A(含子弹)、B通过弹簧不断地相互作用,系统动量和机械能守恒。刚开始弹簧被压缩,A作减速运动,B作加速运动,当弹簧被压缩到最短时,A、B速率相等。接着B继续加速,A继续减速,弹簧形变逐渐恢复,直到恢复原长,B的速率最大,A的速率最小,即此时B的动能达到最大。以后将做周期性的往复运动。则有:v0=()v1 得v1=
10. 1.图中,轻弹簧的一端固定,另一端与滑块B相连,B静止在水平直导轨上,弹簧处在原长状态。另一质量与B相同的滑块A,从导轨上的P点以某一初速度向B滑行。当A滑过距离时,与B相碰,碰撞时间极短,碰后A、B紧贴在一起运动,但互不粘连。已知最后A恰好返回到出发点P并停止。滑块A和B与导轨的滑动摩擦因数都为μ,运动过程中弹簧最大形变量为,重力加速度为。求A从P点出发时的初速度。 L1L21.如图示,一足够长的木板在光滑的水平面上以速度v匀速运动,现将质量为m的物体轻轻地放置在木板上的P点处,已知物体m与木板之间的动摩擦因素为μ,为保持木板的速度不变,从物体m 放到木板上到它相对于木板静止的过程中,对木板施一水平向右的作用力F,那么F 对木板做的功有多大? W=FS2=fs2=μmgvt=mv2解法一:物体m摩擦力作用下做匀加速运动,拉力做的功为: 解法二:由能量守恒定律,拉力F 的功等于物体动能的增加和转化的内能.
W=1/2×mv2+fΔs= 1/2×mv2+f(s2-s1)
= 1/2×mv2 + 1/2×μmgvt=mv2拓展:上题中,若物体m以水平向左的速度v 轻轻地放置在木板上的P点处 ,那么F 对木板做的功有多大?解析:物体m 在摩擦力作用下向左做匀减速运动,经时间t 速度减为0到达Q点,又在摩擦力作用下向右做匀加速运动,经时间t 速度达到v,
f =μmg, a=μg, t = v/a=v/μg
在2t 时间内,物体m 的位移:s1=0
木板的位移:s2=2vt
∴W=Fs2=fs2=μmg×2v× v/μg=2mv2解法三:物体的动能不变,由能量守恒定律,拉力F 的功等于转化的内能.
∴ W=fΔs=f(s2-s1)=fs2=μmg×2vt=2mv2 领悟: ①隔离分析m的时候,参考系是地面而不是木板,所以木板对物体的摩擦力产生的加速度是物体相对于地面的加速度!故分析m的运动时也应该以地面为参考系.②能量观点解题可以使解答过程变得十分简练!所以,通常应该优先考虑能量观点求解! L mMV5.如图所示,一块质量为M长为L的均质板放在很长的光滑水平桌面上,板的左端有一质量为m的物块,物块上连接一根很长的细绳,细绳跨过位于桌面的定滑轮,某人以恒定的速率v向下拉绳,物块最多只能到达板的中央,而此时的右端尚未到桌边定滑轮,试求
(1)物块与板的动摩擦因数及物体刚到达板的中点时板的位移
(2)若板与桌面之间有摩擦,为使物体能达到板的右端,板与桌面间的动摩擦因数范围
(3)若板与桌面之间的动摩擦因数取( 2 )问中的最小值,在物体从板的左端运动到板的右端的过程中,人拉绳的力所做的功(其它阻力 不计) (2) (3)5.如图,平板车质量为M,小木块质量为m,M>m。平板车与小木块通过一水平轻弹簧相连,开始时均静止,车与木块、车与水平地面之间摩擦均不计。现同时对小木块及小车施加等大反向的水平恒力F1和F2的作用,两物体开始运动后,弹簧形变始终在弹性限度内,则关于此后的运动过程有以下说法:①车与木块的速度同时达到最大.②车与木块的速度同时减为零. ③由车、木块和弹簧组成的系统机械能守恒。④由车、木块和弹簧组成的系统总动量时而增加,时而减少。⑤车的速度与木块的速度总是大小相等方向相反。则正确的说法是( )A.①②⑤ B.①② C.③④ D.②③⑤ B1.如图质量为M的足够长的木板,以速度在光滑的水平面上向左运动,一质量为m的小铁块以同样大小的速度从板的左端向右运动,最后二者以共同的速度 做匀速运动。若它们之间的动摩擦因数为。求:
(1)小铁块向右运动的最大距离为多少?
(2)小铁块在木板上滑行多远?(答案:(1)(2)) 3.如图所示,一质量为M,长为l的长方形木板B放在光滑的水平面上,其右端放一质量为m的小物体A(m<M)。现以地面为参照系,给A和B以大小相等,方向相反的初速度使A开始向左运动,B开始向右运动,但最后A刚好没有滑离B板。(1)若已知A和B的初速度大小为v0,求它们最后的速度大小和方向;(2)若初速度的大小未知,求小木块A向左运动到达最远处(从地面上看)离出发点的距离。LB , , 2. 如图所示,A、B是静止在水平地面上完全相同的两块长木板。A的左端和B的右端相接触。两板的质量皆为M=2.0kg,长度=1.0m。C是一质量为m=1.0kg的小物块。现给它一初速度=2.0m/s,使它从B板的左端开始向右滑动。已知地面是光滑的,而C与A、B之间的动摩擦因数皆为=0.10。求最后A、B、C各以多大的速度做匀速运动(重力加速度g取10)13.如图,长木板ab的b端固定一挡板,木板连同挡板的质量为=4.0kg,a、b间距离s=2.0m。木板位于光滑水平面上。在木板a端有一小物块,其质量m=1.0kg,小物块与木板间的动摩擦因数=0.10,它们都处于静止状态。现令小物块以初速=4.0m/s沿木板向前滑动,直到和挡板相碰。碰撞后,小物块恰好回到a端而不脱离木板。求碰撞过程中损失的机械能。2.4J 子弹打木块模型例? 如图3-6,质量为M的木块放在光滑水平面上,现有一质量为m的子弹以速度v0射入木块中。设子弹在木块中所受阻力不变,大小为f,且子弹未射穿木块。若子弹射入木块的深度为D,则木块向前移动距离是多少?系统损失的机械能是多少?例1.一轻质弹簧两端各连接一块质量为m的滑块A和B,A、B静置于光滑水平面上,质量为m/4的子弹以水平速度v0射入A中不再穿出,如图-9所示,求滑块B所获得的最大动能。解析:子弹打入A是个瞬间过程,弹簧还没有来得及被压缩,该过程满足动量守恒。然后A(含子弹)、B通过弹簧不断地相互作用,系统动量和机械能守恒。刚开始弹簧被压缩,A作减速运动,B作加速运动,当弹簧被压缩到最短时,A、B速率相等。接着B继续加速,A继续减速,弹簧形变逐渐恢复,直到恢复原长,B的速率最大,A的速率最小,即此时B的动能达到最大。以后将做周期性的往复运动。则有:v0=()v1 得v1=
同课章节目录
