第二轮专题复习 电磁学综合题[下学期]
文档属性
| 名称 | 第二轮专题复习 电磁学综合题[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 507.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2007-04-25 00:00:00 | ||
图片预览






文档简介
课件47张PPT。电磁学综合题
95年上海 如图示电路中,六个电阻的阻值均相同,由于对称性,电阻R2 上无电流流过,已知电阻R6 所消耗的电功率为1W,则六个电阻所消耗的总功率为 ( )
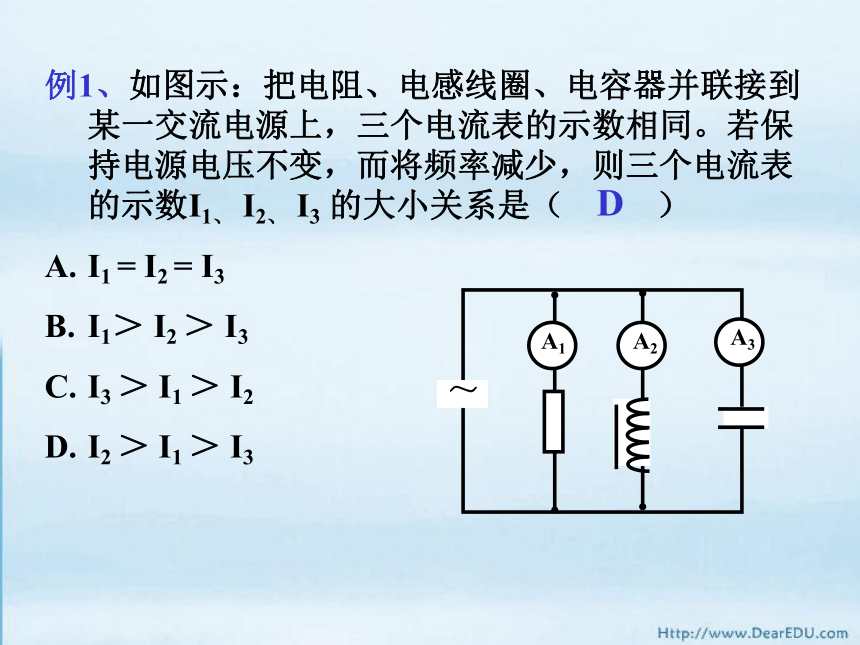
A. 6W B. 5W C. 3W D. 2W解:等效电路如中、右图示:D例1、如图示:把电阻、电感线圈、电容器并联接到某一交流电源上,三个电流表的示数相同。若保持电源电压不变,而将频率减少,则三个电流表的示数I1、 I2、 I3 的大小关系是( )
I1 = I2 = I3
I1> I2 > I3
I3 > I1 > I2
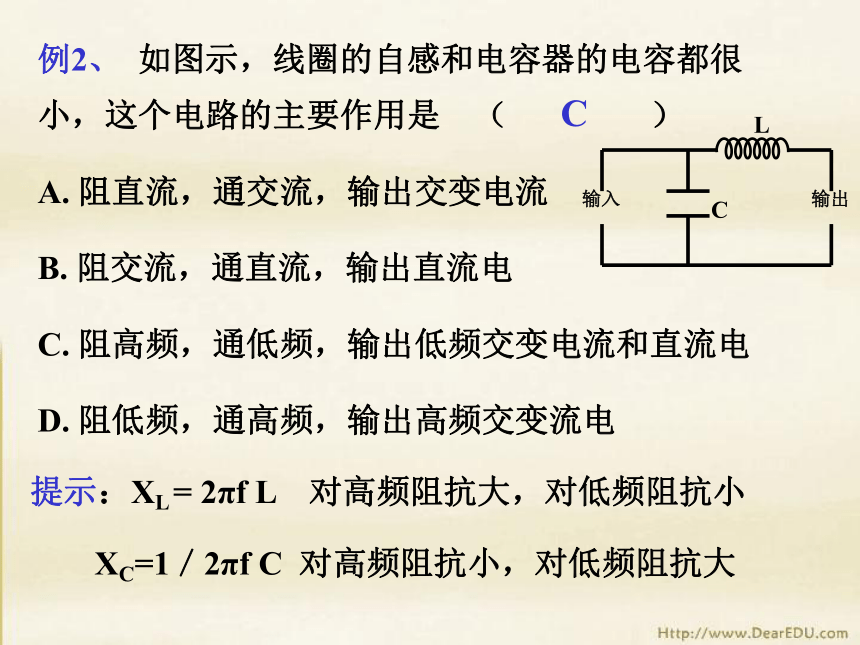
I2 > I1 > I3D例2、 如图示,线圈的自感和电容器的电容都很小,这个电路的主要作用是 ( )
A. 阻直流,通交流,输出交变电流
B. 阻交流,通直流,输出直流电
C. 阻高频,通低频,输出低频交变电流和直流电
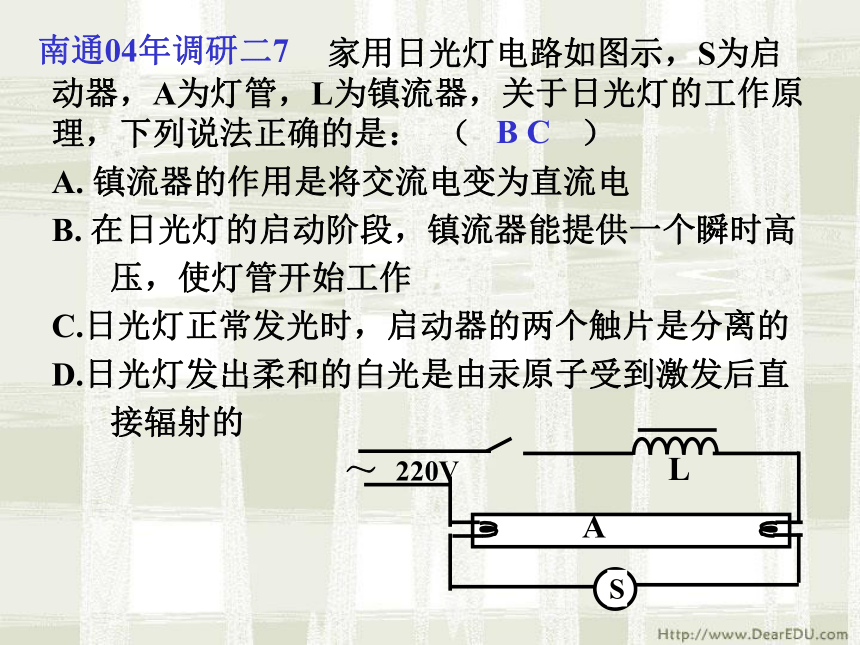
D. 阻低频,通高频,输出高频交变流电提示:XL = 2πf L 对高频阻抗大,对低频阻抗小XC=1/2πf C 对高频阻抗小,对低频阻抗大 C 家用日光灯电路如图示,S为启动器,A为灯管,L为镇流器,关于日光灯的工作原理,下列说法正确的是: ( )
A. 镇流器的作用是将交流电变为直流电
B. 在日光灯的启动阶段,镇流器能提供一个瞬时高
压,使灯管开始工作
C.日光灯正常发光时,启动器的两个触片是分离的
D.日光灯发出柔和的白光是由汞原子受到激发后直
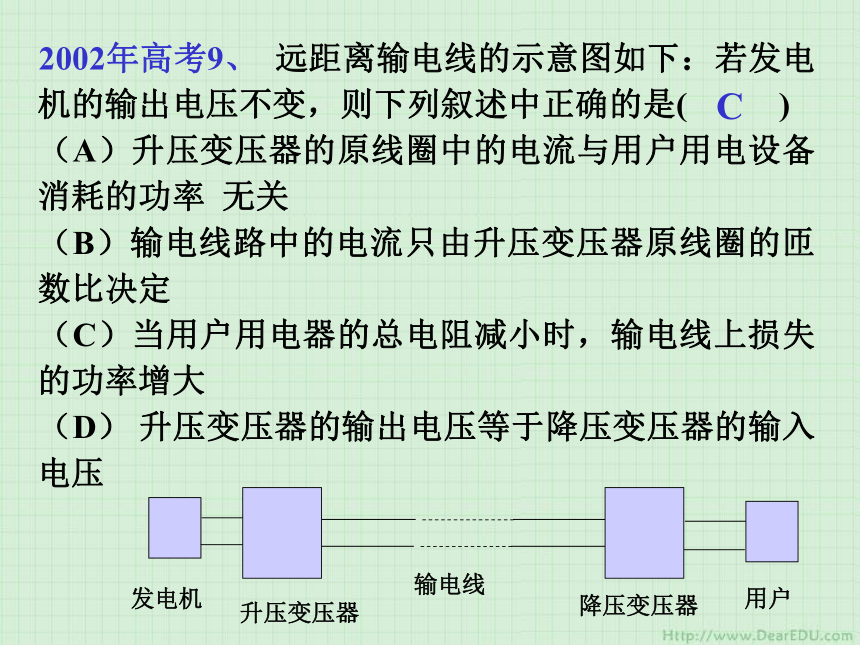
接辐射的南通04年调研二7~B C2002年高考9、? 远距离输电线的示意图如下:若发电机的输出电压不变,则下列叙述中正确的是( )
(A)升压变压器的原线圈中的电流与用户用电设备消耗的功率 无关
(B)输电线路中的电流只由升压变压器原线圈的匝数比决定
(C)当用户用电器的总电阻减小时,输电线上损失的功率增大
(D)?升压变压器的输出电压等于降压变压器的输入电压
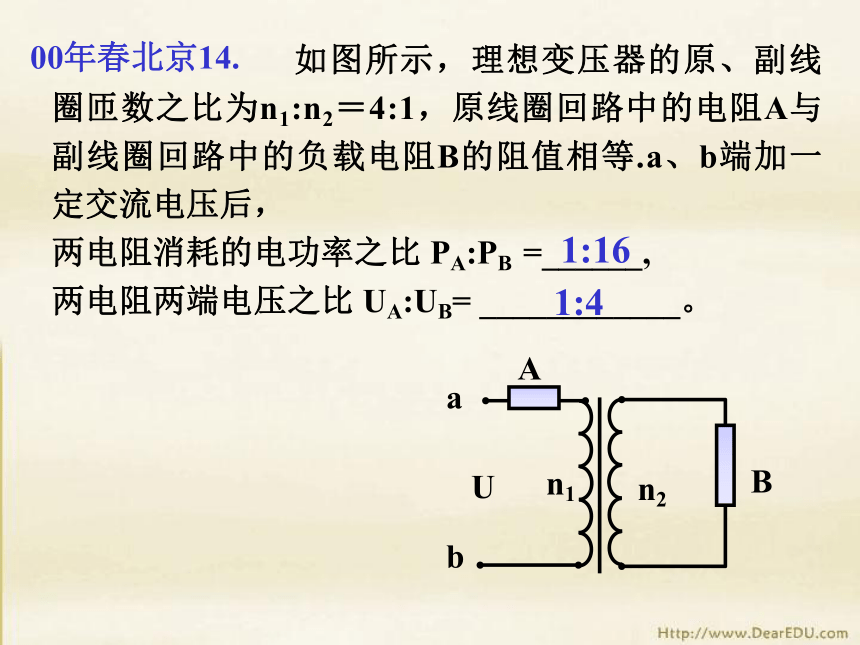
C00年春北京14. 如图所示,理想变压器的原、副线圈匝数之比为n1:n2=4:1,原线圈回路中的电阻A与副线圈回路中的负载电阻B的阻值相等.a、b端加一定交流电压后,
两电阻消耗的电功率之比 PA:PB =______,
两电阻两端电压之比 UA:UB= ____________。1:161:4苏州04年调研9 如图示为一理想变压器的电路图,图中S为单刀双掷开关,P为滑动变阻器R的滑动头,U1为加在原线圈两端的交变电压,,I1为原线圈中的电流,则下列说法中正确的是 ( )
A. 若保持U1及P的位置不变,S由a合到b时, I1将增大
B. 若保持U1及P的位置不变,S由b合到a 时,R消耗的
功率将增大
C.若保持U1不变, S接在a处,使P向上滑时,I1将增大
D. 若保持P的位置不变, S接在a处,使U1增大,
I1将增大解:PR= U22/R
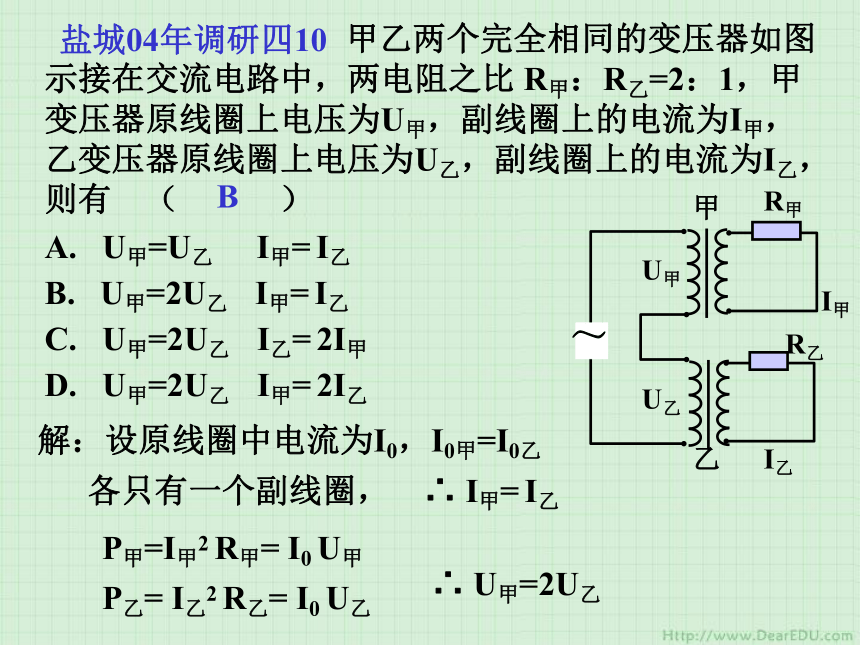
= (n2/n1) 2U12/R=I1U1I1 =(n2/n1) 2U1/RA D盐城04年调研四10 甲乙两个完全相同的变压器如图示接在交流电路中,两电阻之比 R甲:R乙=2:1,甲变压器原线圈上电压为U甲,副线圈上的电流为I甲,乙变压器原线圈上电压为U乙,副线圈上的电流为I乙,则有 ( )A. U甲=U乙 I甲= I乙
B. U甲=2U乙 I甲= I乙
C. U甲=2U乙 I乙= 2I甲
D. U甲=2U乙 I甲= 2I乙解:设原线圈中电流为I0,I0甲=I0乙 各只有一个副线圈, ∴ I甲= I乙P甲=I甲2 R甲= I0 U甲P乙= I乙2 R乙= I0 U乙∴ U甲=2U乙B 例3、 如图所示,匀强磁场方向垂直纸面向里,磁感应强度B=0.20T,OCA金属导轨与OA金属直导轨分别在O点和A点接一阻值为R1 =3.0Ω和R2=6.0 Ω 体积可忽略的定值电阻,导轨OCA的曲线方程为 y=1.0sin(π/3· x) (m),金属棒ab平行于y 轴, 长为1.5m,以速度 v=5.0 m/s 水平向右匀速运动(b点始终在Ox轴上),设金属棒与导轨接触良好,摩擦不计,电路中除了电阻R1和R2外,其余电阻均不计,求:
(1)金属棒在导轨上运动时R1的最大功率
(2)金属棒在导轨上从x=0到x=3m
的运动过程中,外力必须做的功解:(1) ab棒运动时产生感应电动势 E=Byv画出等效电路如图示(不计电源内阻):I 1=E/R1 =1/3× ByvP1= I1 2R1 =1/9× B2 y2v2R1 ∴ P1m=1/9× B2 ym2 v2 R1
=1/9×0.04×1×25×3=1/3 W(2) E=Byv∝y 所以E按正弦规律变化Em =By mv =0.2×1.0×5=1VE有=0.707Vt=x/v=3/5=0.6sR并=3×6/9=2 Ω∴W=Q= E有2/R并×t = 0.5/2×0.6 = 0.15 J 、 如图所示, OACO为置于水平面内的光滑闭合金属导轨, O、C 处分别接有短电阻丝(图中用粗线表示), R1 =4Ω、R2=8 Ω,(导轨其它部分电阻不计),导轨OAC的形状满足方程 y=2 sin(π/3· x) (单位:m),磁感应强度B=0.2T的匀强磁场方向垂直于导轨平面,一足够长的金属棒在水平外力F作用下,以恒定的 速率 v=5.0 m/s 水平向右在导轨上从O点滑动到C点,棒与导轨接触良好且始终保持与OC导轨垂直,不计棒的电阻,求:
(1)外力F 的最大值,
(2)金属棒在导轨上运动时电阻
丝R1上消耗的的最大功率
(3)在滑动过程中通过金属棒
的电流I与时间t 的关系。上海03年高考解:(1) 金属棒匀速运动时产生感应电动势E=BLv ①画出等效电路如图示(不计电源内阻):I =E/R总 ②F外=F安=BIL = B2L2 v/ R总 ③ Lm=2sinπ/2=2m ④R总 = R1 R2 /( R1 + R2 )=8/3 Ω ⑤∴F max = B2Lm2 v/ R总 = 0.22×22 ×5.0 × 3/ 8=0.3N ⑥ (2) P1m= E 2/R1 = B2Lm2 v2/ R1 = 0.22×22 ×5.02 / 4=1W (3)金属棒与导轨接触点间的长度随时间变化L= 2 sin(π/3· x) ( m)x=vtE=BLv ∴I=E/ R总 =Bv/ R总 × 2 sin(π/3· vt )
=3/4× sin(5πt / 3 ) (安) 例4、如图示,电阻均 为 r =0.5Ω的导体AB、CD,质量分别为m、2m,分别在F=6N的外力作用下沿光滑导轨向相反的方向由静止开始运动,匀强磁场垂直纸面向里,磁感应强度B=0.4T,两平行导轨间距离为L=0.5m,导轨的电阻不计,所接电阻R=1 Ω,平行板电容器两板相距1cm,求:
⑴导体AB和CD运动的最大速度
⑵电容器两板间电场强度的大小和方向解:导体AB和CD运动时分别产生感应电动势E1 、E2 E1=BLv1 E2 =BLv2 AB和CD分别受到安培力f的作用
等效电路如图示:由动量守恒定律 mv1+2mv2=0I=(E1+ E2)/(R+2r )=3BLv2 / (R+2r )AB和CD同时达到最大速度时 f=BImL =F v2m =F (R+2r ) /3B2 L2 =6×2 / (3 × 42 ×0.52)=1m/sv1m =2m/sIm=F/BL=6/2=3AUR=IR=3V电场强度E=UR/d=3/0.01=300V /m 方向向左P221/2 如图所示, 竖直放置的光滑平行金属导轨, 相距l , 导轨一端接有一个电容器 , 电容量为C, 匀强磁场垂直纸面向里, 磁感应强度为B, 质量为m的金属棒ab可紧贴导轨自由滑动. 现让ab由静止下滑, 不考虑空气阻力, 也不考虑任何部分的电阻和自感作用. 问金属棒的做什么运动?棒落地时的速度为多大?解:ab在mg 作用下加速运动,经时间 t ,速度增为v,a =v / t产生感应电动势 E=Bl v 电容器带电量 Q=CE=CBl v感应电流I=Q/t=CBL v/ t=CBl a产生安培力F=BIl =CB2 l 2a由牛顿运动定律 mg-F=mama= mg - CB2 l 2aa= mg / (m+C B2 l 2)∴ab做初速为零的匀加直线运动, 加速度 a= mg / (m+C B2 l 2)落地速度为例 在光滑的水平面上,有一竖直向下的匀强磁场,分布在宽度为L 的区域内, 现有一边长为d (d<L )的正方形闭合线框以垂直于磁场边界的初速度v0滑过磁场,线框刚好能穿过磁场,则线框在滑进磁场的过程中产生的热量Q1与滑出磁场的过程中产生的热量Q2之比为 ( )
A. 1:1 B. 2:1 C. 3:1 D. 4:1解:由动量定理 F Δt=B2 L2 d /R=mv0 – mv1 备注 F Δt=B2 L2 d /R= mv1-0∴v0 =2v1由能量守恒定律1/2 mv02 - 1/2 mv12 = Q11/2 mv12 = Q2∴ Q1/ Q2= 3:1 C下页备注设线框即将进入磁场时的速度为v0,全部进入磁场时的速度为vt将线框进入的过程分成很多小段,每一段的运动可以看成是
速度为vi 的匀速运动, 对每一小段,由动量定理: f1 Δt=B2 L2 v0 Δt /R = mv0 – mv1 (1) f2 Δt=B2 L2 v1 Δt /R = mv1 – mv2 (2)f3 Δt=B2 L2 v2 Δt /R = mv2 – mv3 (3)f4 Δt=B2 L2 v3 Δt /R = mv3 – mv4 (4)…… ……
fn Δt=B2 L2 vn-1 Δt /R = mvn-1 – mvt (n)v0 Δt+ v1 Δt + v2 Δt + v3 Δt +……+ vn-1 Δt + vn Δt =d 将各式相加,得B2 L2 d /R = mv0 – mvt 可见速度的变化跟位移成线性关系 如图示,匀强磁场的磁感应强度为B,导体棒ab与光滑导轨接触良好,有效长度为L,外电阻为R ,现用外力使导体棒以O O′为平衡位置做简谐运动,其周期为T,棒经O O′时的速度为V,试求:将棒从左边最大位置移至平衡位置的过程中,外力所做的功(已知棒的质量为m)例5解:ab做简谐运动时的速度为v,则产生的感应电动势为:E=BLv=BLVsinωt ——正弦交流电其最大值为Em=BLV有效值为E=0.707BLV产生的感应电流功率为P=E2 / R=(BLV)2/ 2R运动的时间为 t=T/4产生的感应电能为W电=Pt= (BLV)2T/ 8R由能量守恒定律得WF=W电+1/2 m V2 =(BLV)2T/ 8R+ 1/2 m V2题目练习、 如图示为间距为L 的光滑平行金属导轨,水平地放在竖直方向的磁感应强度为B的匀强磁场中,一端电阻R,一电阻是r、质量为m的导体棒ab放置在导轨上,在外力F作用下从t=0的时刻开始运动,其速度随时间的变化规律为V=Vmsin ωt,不计导轨电阻,试求:
⑴从t=0到t=2π/ω时间内电阻R产生的热量
⑵从t=0到t=π/ 2 ω时间内外力F所做的功解:ab运动时的速度为 V=Vmsin ωt ,则产生的感应电动势为:E=BLV=BLVmsinωt ——正弦交流电其最大值为Em=BLVm有效值为E=0.71BLVm I=E /(R+r)电阻R产生的热量为Q= I2 Rt
= (0.71BLVm)2 / (R+r)2× R ×2π/ω
= π R B 2 L 2 Vm2 / ω(R+r)2由能量守恒定律,外力F所做的功转化为电能和动能WF=W电+1/2 m V2 = π/ 2 ω × (BLVm)2/2(R+r)
+ 1/2 m V2 = π ×B 2 L 2 Vm2/4 ω(R+r) + 1/2 m Vm2 题目P212/3 如图示,螺线管匝数n=4,截面积.S=0.1m2,管内匀强磁场以B1/t=10T/s 逐渐增强, 螺线管两端分别与两根竖直平面内的平行光滑直导轨相接, 垂直导轨的水平匀强磁场B2=2T, 现在导轨上垂直放置一根质量m=0.02kg, 长l=0.1m的铜棒,回路总电阻为R=5,试求铜棒从静止下落的最大速度. (g=10m/s2)解:螺线管产生感生电动势 E1=nS B1/t=4V 方向如图示I1 =0.8A F1=B2 I1 L=0.16N mg=0.2N mg > F1 ab做加速运动,又产生感应电动势E2,(动生电动势)当达到稳定状态时,F2 =mg=0.2NF2 =BI2 L I2 =1AI2 =(E1 +E2 )/R=(4+E2)/5 =1AE2 =1V=BLvmvm=5m/s 2003年江苏高考18(13分)如图所示,两根平行金属导轨固定在水平桌面上,每根导轨每米的电阻为r0=0.10Ω/m,导轨的端点P、Q用电阻可忽略的导线相连,两导轨间的距离 l =0.20m.有随时间变化的匀强磁场垂直于桌面,已知磁感强度B与时间t 的关系为B=kt,比例系数k=0.020T/s.一电阻不计的金属杆可在导轨上无摩擦地滑动,在滑动过程中保持与导轨垂直,在t=0时刻,金属杆紧靠在P、Q端,在外力作用下,杆以恒定的加速度从静止开始向导轨的另一端滑动,求在t=6.0s时金属杆所受的安培力. 解:以 a 表示金属杆运动的加速度,在t 时刻,金属杆与初始位置的距离L=1/2× a t2此时杆的速度v= a t,这时,杆与导轨构成的回路的面积S=Ll ,回路中的感应电动势E=SΔB/ Δt + Bl v =Sk+Bl v回路的总电阻R=2Lr0回路中的感应电流i =E/R作用于杆的安培力 F =B l i解得 F=3k2 l 2 t / 2r0 ,代入数据为F=1.44×10 -3 N 例6(2000年高考科研试题) 如图所示,两根相距为d的足够长的平行金属导轨位于水平的xOy平面内,一端接有阻值为R的电阻.在x> 0 的一侧存在沿竖直方向的非均匀磁场,磁感强度B随x的增大而增大,B=kx,式中的k是一常量.一金属直杆与金属导轨垂直,可在导轨上滑动.当t=0 时位于x= 0处,速度为v0,方向沿x轴的正方向.在运动过程中,有一大小可调节的外力F作用于金属杆以保持金属杆的加速度恒定,大小为a,方向沿x轴的负方向.设除外接的电阻R外,所有其他电阻都可以忽略.问:
(1)该回路中的感应电流持续的时间多长? (2)当金属杆的速度大小为v0/2 时,回路中的感应电动势有多大?解 : (1)金属杆在导轨上先是向右做加速度为a的匀减速直线运动,到导轨右方最远处速度为零,后又沿导轨向左做加速度为a的匀加速直线运动.当过了y 轴后,由于已离开了磁场区,故回路不再有感应电流.以t1表示金属杆做匀减速运动的时间,有t1=v0/ a.从而,回路中感应电流持续的时间 T=2t1=2v0/a.(2)以x1表示金属杆的速度变为v1=v0/2 时它所在的x 坐标,由 v12=v02-2ax1,可得 x1=3v02/8a,从而,此时金属杆所在处的磁感强度 B1=kx1=3kv02/8a所以,此时回路中的感应电动势E1=B1v1d=3kv03d/16 a. 例7:水平放置的导轨处于垂直轨道平面的匀强磁场中,今从静止起用力拉金属棒ab,若拉力为恒力,经t1 秒ab的速度为v,加速度为a1 ,最终速度为2v, 若拉力的功率恒定,经t2秒ab的速度为v,加速度为a2 ,最终速度为2v, 求 a1和a2的关系解:拉力为恒力:最终有 F=F安=B2 L2 ×2v/Ra1= (F- B2 L2 v/R) / m=F/m - B2 L2 v / mR= B2 L2 v / mR拉力的功率恒定:F′= F安= P/2v = B2 L2 ×2v/R∴P/v= 4B2 L2 v/Ra2=( F2′- F安′) / m
= [P/v - B2 L2 v/R]/m= 3B2 L2 v / mRa2 = 3a1 例8、 如图示,U形导体框架的宽度L=0.5m,电阻忽略不计,其所在平面与水平面成α=30°,一根质量m=0.1kg、有效电阻R=0.5Ω的导体棒MN垂直跨放在U形框架上,离PQ的距离为b=0.2m,整个装置处于与滑轨平面正交、磁感应强度按B=0.2t2 T规律变化的磁场中,t=0时导体恰好静止,(g=10m/s2)求:
⑴ 经过多少时间导体开始滑动
⑵ 这段时间内通过导体棒横截面的电量解:⑴t=0时 B=0,恰好静止 fm =mgsin 30°=0.5NE=Δφ/ Δ t=Lb ΔB/ Δ t=0.5×0.2 ×0.4t=0.04t伏I=E/R=0.08 t 安导体开始滑动时,受力如图示BIL= fm +mgsin 30°= 1N0.2 t2×0.08 t×0.5=1t3=1/0.008 t=5秒例9、 一质量为M=1kg 的小车上固定有一质量为m = 0.2 kg ,高 l = 0.05m、电阻 R=100Ω的100匝矩形线圈,一起静止在光滑水平面上,现有一质量为m0 的子弹以v0=110m/s 的水平速度射入小车中,并随小车线圈一起进入一与线圈平面垂直,磁感强度 B=1.0T 的水平匀强磁场中如图甲所地, 小车运动过程的v-s 图象如图乙所示。求:
(1)子弹的质量m0为 。
(2)图乙中s =10cm时线圈中的电流强度I为 。
(3在进入过程中通过线圈某一截面的电量为 。
(4)求出线圈小车通过磁场的过程中线圈电阻的发热量为
。解:⑴由图象可知:进入磁场时 ,v1=10m/s由动量守恒定律m0v0 =(M+m+m0)v1 m0 =0.12kg⑵由图象可知:s=10cm v2 =8m/sE=nBLv2=100×1×0.05×8=40V I=E/R=0.4A⑶由图象可知:线圈宽度为 d=10cmq=I Δ t=n Δ Ф/R=100×1×0.1×0.05/100=5×10-3 C ⑷由图象可知:出磁场时 ,vt=2m/sQ=1/2×(M+m+m0)(v12 –vt2)=1/2×1.32×(100-4)=63.4J 思考:为什么v-s图象是三段折线?答:见备注。03年上海高考18、 (7分)图1为某一热敏电阻R(电阻值随温度的改变而改变,且对温度很敏感)的I-U关系曲线图。
⑴为了通过测量得到图1所示I-U关系的完整曲线,在图2和图3两个电路中应选择的是图 ;简要说明理由:
。(电源电动势为9V,内阻不计,滑线变阻器的阻值为0-100Ω)
⑵在图4电路中,电源电压恒为9V,电流表读数为70mA,定值电阻R1=250Ω。由热敏电阻的I-U关系曲线可知,热敏电阻两端的电压为________V;电阻R2的阻值为 Ω。
⑶举出一个可以应用热敏电阻的例子:_____________。2电压可从0V调到所需电压,调节范围较大 解: ⑵ I1=9/250=0.036A=36mA I2=34mA 由图1得 UR=5.2V 5.2 R2 =(9-5.2) / 0.034=111.8 Ω 111.6—112.0 热敏温度计 如图示, Ⅰ、 Ⅲ为两匀强磁场区,磁感应强度均为B,方向如图示,两区域中间为宽L/2的无磁场区Ⅱ,有一边长为L、粗细均匀、各边电阻为R的正方形金属框abcd置于区域Ⅰ,ab 边与磁场边界平行,现拉着金属框以速度v水平向右匀速运动,则
(1)分别求出当ab边刚进入中央无磁场区Ⅱ和进入磁场区Ⅲ时,通过ab 边的电流大小和方向.
(2)画出金属框从区域Ⅰ刚出来到完全拉入区域Ⅲ过程中水平拉力与时间的关系图象.
(3)求上述 (2)过程
中拉力所做的功04年南师大模考16解:(1)ab刚进入Ⅱ,cd边产生EE=BLv I1= BLv/4R 顺时针方向 ab刚进入Ⅲ,ab、cd边都产生E I2= 2BLv/4R 逆时针方向 (2) ab刚进入Ⅱ,F1=BI1L=B2L2v/4Rab刚进入Ⅲ,F2= 2BI2L= B2L2v/R ab进入Ⅲ,cd 还在Ⅱ,ab边产生E
F3=BI3L =BI1L =B2L2v/4R三段时间都为L/2vF-t 图象如右图示(3) W=F1L/2+ F2L/2+ F3L/2
= 3B2L3v/4R例10、如图所示,PR是一块长为L=4米的绝缘平板固定在水平地面上,整个空间有一个平行于PR的匀强电场E,在板的右半部分有一个垂直于纸面向外的匀强磁场B,一个质量为m=0.1千克、带电量为q=0.5库仑的物体,从板的P端由静止开始在电场力和摩擦力的作用下向右做匀加速运动,进入磁场后恰能做匀速运动。当物体碰到板R端挡板后被弹回,若在碰撞瞬间撤去电场,物体返回时在磁场中仍做匀速运动,离开磁场后做匀减速运动停在C点,PC=L/4,物体与平板间的动摩擦因素为μ=0.4。求:
?⑴判断物体带电性质,正电还是负电荷?
⑵物体与挡板碰撞前后的速度v1和v2;
⑶磁感强度B的大小;
⑷电场强度E的大小和方向 。解:返回时,R→D无电场力,能作匀速运动,表明无摩擦力qv2B向上,物体带正电。受力如图a 示 qv2B=mg ⑴D → C ,无磁场力, -μmg×0.25L=1/2×mv22 ⑵ P →D ,加速,E向右 (qE – μmg)×1/2L =1/2×mv12 ⑶D →R ,受力如图b 示 qE= μ(mg+ qv1B) ⑷ 解⑴⑵⑶⑷得
qv1B=2N qv2B=1N qE=1.2N
v1=5.66m/s
v2=2.83m/s
B=0.71T
E=2.4V/m 方向向右 例11、某空间存在着一个变化的电场和一个变化的磁场,如图示,电场方向由B到C,在A点,从t=1s末开始,每隔2s有一个相同的带电粒子(不计重力)沿AB方向(垂直于BC)以速度v 射出,恰好能击中C点,若AC=2BC,且粒子在AC间运动的时间小于1s。试问:
1. 图线上E和B的比值有多大?磁感应强度B 的方向如何?
2. 若第一个粒子击中C点的时刻已知为(1s+Δt ),那么第二个粒子击中C点为何时刻?解:在1s末,粒子在磁场中受洛仑兹力做匀速圆周运动,令BC=y不难得到: AC=2y, R=mv/qB=2y ∴ B=mv / 2qy在3s末,第二个粒子在电场中受电场力做类似平抛运动,∴∴E/B=4v/3第一个粒子经过t击中C点,t=1/6T=m/3qB第二个粒子击中C点经过 t 秒第二个粒子击中C点的时刻为3+ t 秒04年江苏高考12 (12分)某同学对黑箱(见图1)中一个电学元件的伏安特性进行研究.通过正确测量,他发现该元件两端的电压Uab(Uab=Ua-Ub)与流过它的电流I 之间的变化关系有如下规律
①当 - 15V < Uab < 0V 时,I 近似为零.
②当Uab≥0时,Uab和I 的实验数据见下表:(1)在图2中画出Uab≥0时该元件的伏安特性曲线.(可用铅笔作图)
(2)根据上述实验事实.该元件具有的特性是______________________。见下页单向导电性(3)若将此黑箱接入图3电路中,并在该电路的cd两端输入如图4(甲)所示的方波电压信号ucd,请在图4(乙)中定性画出负载电阻RL上的电压信号uef的波形.题目04年江苏高考13 (14分)如图所示,一个变压器(可视为理想变压器)的原线圈接在220V的市电上,向额定电压为1.80×104V的霓虹灯供电,使它正常发光.为了安全,需在原线圈回路中接入熔断器,使副线圈电路中电流超过12mA时,熔丝就熔断.
(1)熔丝的熔断电流是多大? (2)当副线圈电路中电流为10mA时.变压器的输入功率是多大?解:(1)设原、副线圈上的电压、电流分别为U1、U2、I1、I2.根据理想变压器的输入功率等于输出功率,有 I1 U1= I2U2.当I2=12 mA时,I1 即为熔断电流.代人数据,得 I1 =0.98 A (2) 设副线圈中电流为 I2 ′=10 mA时,
变压器的输入功率为P1 根据理想变压器的输入功
率等于输出功率,有P1= I2′U2代人数据,得 P1 =180 W 04年江苏高考14 (14分)如图所示的电路中,电源电动势E=6.00V,其内阻可忽略不计.电阻的阻值分别为R1=2.4 kΩ、R2=4.8kΩ,电容器的电容C=4.7μF.闭合开关S,待电流稳定后,用电压表测R1两端的电压,其稳定值为1.50V.
(1)该电压表的内阻为多大?
(2)由于电压表的接入,电容器的带电量变化了多少?解: (1)设电压表的内阻为RV,测得R1两端的电压为U1, R1与RV并联后的总电阻为R,则有 由串联电路的规律联立①②,得代入数据,可得 RV =4.8kΩ (2)电压表接入前,电容器上的电压UC等于电阻R2上的电压, R1两端的电压为UR1 ,则又接入电压表后,电容器上的电压为由于电压表的接入,电容器带电量增加了 由以上各式解得代入数据,可得 04年江苏高考17 17. (16分)汤姆生用来测定电子的比荷(电子的电荷量与质量之比)的实验装置如图所示,真空管内的阴极K发出的电子(不计初速、重力和电子间的相互作用)经加速电压加速后,穿过A'中心的小孔沿中心轴O1O的方向进入到两块水平正对放置的平行极板P和P'间的区域.当极板间不加偏转电压时,电子束打在荧光屏的中心O点处,形成了一个亮点;加上偏转电压U后,亮点偏离到O'点,(O'与O点的竖直间距为d,水平间距可忽略不计.此时,在P和P'间的区域,再加上一个方向垂直于纸面向里的匀强磁场.调节磁场的强弱,当磁感应强度的大小为B时,亮点重新回到O点.已知极板水平方向的长度为L1,极板间距为b,极板右端到荧光屏的距离为L2(如图所示). (1)求打在荧光屏O点的电子速度的大小。
(2)推导出电子的比荷的表达式 解:(1)当电子受到的电场力与洛沦兹力平衡时,电子做匀速直线运动,亮点重新回复到中心O点,设电子的速度为v,则evB=eE得 v=E/B即 v=U/Bb(2)当极板间仅有偏转电场时,电子以速度v进入后,竖直方向作匀加速运动,加速度为 a = eU / mb电子在水平方向作匀速运动,在电场内的运动时间为 t 1=L/v这样,电子在电场中,竖直向上偏转的距离为 离开电场时竖直向上的分速度为 电子离开电场后做匀速直线运动,经t2时间到达荧光屏t2=L2 /v t2时间内向上运动的距离为 这样,电子向上的总偏转距离为 可解得题目
95年上海 如图示电路中,六个电阻的阻值均相同,由于对称性,电阻R2 上无电流流过,已知电阻R6 所消耗的电功率为1W,则六个电阻所消耗的总功率为 ( )
A. 6W B. 5W C. 3W D. 2W解:等效电路如中、右图示:D例1、如图示:把电阻、电感线圈、电容器并联接到某一交流电源上,三个电流表的示数相同。若保持电源电压不变,而将频率减少,则三个电流表的示数I1、 I2、 I3 的大小关系是( )
I1 = I2 = I3
I1> I2 > I3
I3 > I1 > I2
I2 > I1 > I3D例2、 如图示,线圈的自感和电容器的电容都很小,这个电路的主要作用是 ( )
A. 阻直流,通交流,输出交变电流
B. 阻交流,通直流,输出直流电
C. 阻高频,通低频,输出低频交变电流和直流电
D. 阻低频,通高频,输出高频交变流电提示:XL = 2πf L 对高频阻抗大,对低频阻抗小XC=1/2πf C 对高频阻抗小,对低频阻抗大 C 家用日光灯电路如图示,S为启动器,A为灯管,L为镇流器,关于日光灯的工作原理,下列说法正确的是: ( )
A. 镇流器的作用是将交流电变为直流电
B. 在日光灯的启动阶段,镇流器能提供一个瞬时高
压,使灯管开始工作
C.日光灯正常发光时,启动器的两个触片是分离的
D.日光灯发出柔和的白光是由汞原子受到激发后直
接辐射的南通04年调研二7~B C2002年高考9、? 远距离输电线的示意图如下:若发电机的输出电压不变,则下列叙述中正确的是( )
(A)升压变压器的原线圈中的电流与用户用电设备消耗的功率 无关
(B)输电线路中的电流只由升压变压器原线圈的匝数比决定
(C)当用户用电器的总电阻减小时,输电线上损失的功率增大
(D)?升压变压器的输出电压等于降压变压器的输入电压
C00年春北京14. 如图所示,理想变压器的原、副线圈匝数之比为n1:n2=4:1,原线圈回路中的电阻A与副线圈回路中的负载电阻B的阻值相等.a、b端加一定交流电压后,
两电阻消耗的电功率之比 PA:PB =______,
两电阻两端电压之比 UA:UB= ____________。1:161:4苏州04年调研9 如图示为一理想变压器的电路图,图中S为单刀双掷开关,P为滑动变阻器R的滑动头,U1为加在原线圈两端的交变电压,,I1为原线圈中的电流,则下列说法中正确的是 ( )
A. 若保持U1及P的位置不变,S由a合到b时, I1将增大
B. 若保持U1及P的位置不变,S由b合到a 时,R消耗的
功率将增大
C.若保持U1不变, S接在a处,使P向上滑时,I1将增大
D. 若保持P的位置不变, S接在a处,使U1增大,
I1将增大解:PR= U22/R
= (n2/n1) 2U12/R=I1U1I1 =(n2/n1) 2U1/RA D盐城04年调研四10 甲乙两个完全相同的变压器如图示接在交流电路中,两电阻之比 R甲:R乙=2:1,甲变压器原线圈上电压为U甲,副线圈上的电流为I甲,乙变压器原线圈上电压为U乙,副线圈上的电流为I乙,则有 ( )A. U甲=U乙 I甲= I乙
B. U甲=2U乙 I甲= I乙
C. U甲=2U乙 I乙= 2I甲
D. U甲=2U乙 I甲= 2I乙解:设原线圈中电流为I0,I0甲=I0乙 各只有一个副线圈, ∴ I甲= I乙P甲=I甲2 R甲= I0 U甲P乙= I乙2 R乙= I0 U乙∴ U甲=2U乙B 例3、 如图所示,匀强磁场方向垂直纸面向里,磁感应强度B=0.20T,OCA金属导轨与OA金属直导轨分别在O点和A点接一阻值为R1 =3.0Ω和R2=6.0 Ω 体积可忽略的定值电阻,导轨OCA的曲线方程为 y=1.0sin(π/3· x) (m),金属棒ab平行于y 轴, 长为1.5m,以速度 v=5.0 m/s 水平向右匀速运动(b点始终在Ox轴上),设金属棒与导轨接触良好,摩擦不计,电路中除了电阻R1和R2外,其余电阻均不计,求:
(1)金属棒在导轨上运动时R1的最大功率
(2)金属棒在导轨上从x=0到x=3m
的运动过程中,外力必须做的功解:(1) ab棒运动时产生感应电动势 E=Byv画出等效电路如图示(不计电源内阻):I 1=E/R1 =1/3× ByvP1= I1 2R1 =1/9× B2 y2v2R1 ∴ P1m=1/9× B2 ym2 v2 R1
=1/9×0.04×1×25×3=1/3 W(2) E=Byv∝y 所以E按正弦规律变化Em =By mv =0.2×1.0×5=1VE有=0.707Vt=x/v=3/5=0.6sR并=3×6/9=2 Ω∴W=Q= E有2/R并×t = 0.5/2×0.6 = 0.15 J 、 如图所示, OACO为置于水平面内的光滑闭合金属导轨, O、C 处分别接有短电阻丝(图中用粗线表示), R1 =4Ω、R2=8 Ω,(导轨其它部分电阻不计),导轨OAC的形状满足方程 y=2 sin(π/3· x) (单位:m),磁感应强度B=0.2T的匀强磁场方向垂直于导轨平面,一足够长的金属棒在水平外力F作用下,以恒定的 速率 v=5.0 m/s 水平向右在导轨上从O点滑动到C点,棒与导轨接触良好且始终保持与OC导轨垂直,不计棒的电阻,求:
(1)外力F 的最大值,
(2)金属棒在导轨上运动时电阻
丝R1上消耗的的最大功率
(3)在滑动过程中通过金属棒
的电流I与时间t 的关系。上海03年高考解:(1) 金属棒匀速运动时产生感应电动势E=BLv ①画出等效电路如图示(不计电源内阻):I =E/R总 ②F外=F安=BIL = B2L2 v/ R总 ③ Lm=2sinπ/2=2m ④R总 = R1 R2 /( R1 + R2 )=8/3 Ω ⑤∴F max = B2Lm2 v/ R总 = 0.22×22 ×5.0 × 3/ 8=0.3N ⑥ (2) P1m= E 2/R1 = B2Lm2 v2/ R1 = 0.22×22 ×5.02 / 4=1W (3)金属棒与导轨接触点间的长度随时间变化L= 2 sin(π/3· x) ( m)x=vtE=BLv ∴I=E/ R总 =Bv/ R总 × 2 sin(π/3· vt )
=3/4× sin(5πt / 3 ) (安) 例4、如图示,电阻均 为 r =0.5Ω的导体AB、CD,质量分别为m、2m,分别在F=6N的外力作用下沿光滑导轨向相反的方向由静止开始运动,匀强磁场垂直纸面向里,磁感应强度B=0.4T,两平行导轨间距离为L=0.5m,导轨的电阻不计,所接电阻R=1 Ω,平行板电容器两板相距1cm,求:
⑴导体AB和CD运动的最大速度
⑵电容器两板间电场强度的大小和方向解:导体AB和CD运动时分别产生感应电动势E1 、E2 E1=BLv1 E2 =BLv2 AB和CD分别受到安培力f的作用
等效电路如图示:由动量守恒定律 mv1+2mv2=0I=(E1+ E2)/(R+2r )=3BLv2 / (R+2r )AB和CD同时达到最大速度时 f=BImL =F v2m =F (R+2r ) /3B2 L2 =6×2 / (3 × 42 ×0.52)=1m/sv1m =2m/sIm=F/BL=6/2=3AUR=IR=3V电场强度E=UR/d=3/0.01=300V /m 方向向左P221/2 如图所示, 竖直放置的光滑平行金属导轨, 相距l , 导轨一端接有一个电容器 , 电容量为C, 匀强磁场垂直纸面向里, 磁感应强度为B, 质量为m的金属棒ab可紧贴导轨自由滑动. 现让ab由静止下滑, 不考虑空气阻力, 也不考虑任何部分的电阻和自感作用. 问金属棒的做什么运动?棒落地时的速度为多大?解:ab在mg 作用下加速运动,经时间 t ,速度增为v,a =v / t产生感应电动势 E=Bl v 电容器带电量 Q=CE=CBl v感应电流I=Q/t=CBL v/ t=CBl a产生安培力F=BIl =CB2 l 2a由牛顿运动定律 mg-F=mama= mg - CB2 l 2aa= mg / (m+C B2 l 2)∴ab做初速为零的匀加直线运动, 加速度 a= mg / (m+C B2 l 2)落地速度为例 在光滑的水平面上,有一竖直向下的匀强磁场,分布在宽度为L 的区域内, 现有一边长为d (d<L )的正方形闭合线框以垂直于磁场边界的初速度v0滑过磁场,线框刚好能穿过磁场,则线框在滑进磁场的过程中产生的热量Q1与滑出磁场的过程中产生的热量Q2之比为 ( )
A. 1:1 B. 2:1 C. 3:1 D. 4:1解:由动量定理 F Δt=B2 L2 d /R=mv0 – mv1 备注 F Δt=B2 L2 d /R= mv1-0∴v0 =2v1由能量守恒定律1/2 mv02 - 1/2 mv12 = Q11/2 mv12 = Q2∴ Q1/ Q2= 3:1 C下页备注设线框即将进入磁场时的速度为v0,全部进入磁场时的速度为vt将线框进入的过程分成很多小段,每一段的运动可以看成是
速度为vi 的匀速运动, 对每一小段,由动量定理: f1 Δt=B2 L2 v0 Δt /R = mv0 – mv1 (1) f2 Δt=B2 L2 v1 Δt /R = mv1 – mv2 (2)f3 Δt=B2 L2 v2 Δt /R = mv2 – mv3 (3)f4 Δt=B2 L2 v3 Δt /R = mv3 – mv4 (4)…… ……
fn Δt=B2 L2 vn-1 Δt /R = mvn-1 – mvt (n)v0 Δt+ v1 Δt + v2 Δt + v3 Δt +……+ vn-1 Δt + vn Δt =d 将各式相加,得B2 L2 d /R = mv0 – mvt 可见速度的变化跟位移成线性关系 如图示,匀强磁场的磁感应强度为B,导体棒ab与光滑导轨接触良好,有效长度为L,外电阻为R ,现用外力使导体棒以O O′为平衡位置做简谐运动,其周期为T,棒经O O′时的速度为V,试求:将棒从左边最大位置移至平衡位置的过程中,外力所做的功(已知棒的质量为m)例5解:ab做简谐运动时的速度为v,则产生的感应电动势为:E=BLv=BLVsinωt ——正弦交流电其最大值为Em=BLV有效值为E=0.707BLV产生的感应电流功率为P=E2 / R=(BLV)2/ 2R运动的时间为 t=T/4产生的感应电能为W电=Pt= (BLV)2T/ 8R由能量守恒定律得WF=W电+1/2 m V2 =(BLV)2T/ 8R+ 1/2 m V2题目练习、 如图示为间距为L 的光滑平行金属导轨,水平地放在竖直方向的磁感应强度为B的匀强磁场中,一端电阻R,一电阻是r、质量为m的导体棒ab放置在导轨上,在外力F作用下从t=0的时刻开始运动,其速度随时间的变化规律为V=Vmsin ωt,不计导轨电阻,试求:
⑴从t=0到t=2π/ω时间内电阻R产生的热量
⑵从t=0到t=π/ 2 ω时间内外力F所做的功解:ab运动时的速度为 V=Vmsin ωt ,则产生的感应电动势为:E=BLV=BLVmsinωt ——正弦交流电其最大值为Em=BLVm有效值为E=0.71BLVm I=E /(R+r)电阻R产生的热量为Q= I2 Rt
= (0.71BLVm)2 / (R+r)2× R ×2π/ω
= π R B 2 L 2 Vm2 / ω(R+r)2由能量守恒定律,外力F所做的功转化为电能和动能WF=W电+1/2 m V2 = π/ 2 ω × (BLVm)2/2(R+r)
+ 1/2 m V2 = π ×B 2 L 2 Vm2/4 ω(R+r) + 1/2 m Vm2 题目P212/3 如图示,螺线管匝数n=4,截面积.S=0.1m2,管内匀强磁场以B1/t=10T/s 逐渐增强, 螺线管两端分别与两根竖直平面内的平行光滑直导轨相接, 垂直导轨的水平匀强磁场B2=2T, 现在导轨上垂直放置一根质量m=0.02kg, 长l=0.1m的铜棒,回路总电阻为R=5,试求铜棒从静止下落的最大速度. (g=10m/s2)解:螺线管产生感生电动势 E1=nS B1/t=4V 方向如图示I1 =0.8A F1=B2 I1 L=0.16N mg=0.2N mg > F1 ab做加速运动,又产生感应电动势E2,(动生电动势)当达到稳定状态时,F2 =mg=0.2NF2 =BI2 L I2 =1AI2 =(E1 +E2 )/R=(4+E2)/5 =1AE2 =1V=BLvmvm=5m/s 2003年江苏高考18(13分)如图所示,两根平行金属导轨固定在水平桌面上,每根导轨每米的电阻为r0=0.10Ω/m,导轨的端点P、Q用电阻可忽略的导线相连,两导轨间的距离 l =0.20m.有随时间变化的匀强磁场垂直于桌面,已知磁感强度B与时间t 的关系为B=kt,比例系数k=0.020T/s.一电阻不计的金属杆可在导轨上无摩擦地滑动,在滑动过程中保持与导轨垂直,在t=0时刻,金属杆紧靠在P、Q端,在外力作用下,杆以恒定的加速度从静止开始向导轨的另一端滑动,求在t=6.0s时金属杆所受的安培力. 解:以 a 表示金属杆运动的加速度,在t 时刻,金属杆与初始位置的距离L=1/2× a t2此时杆的速度v= a t,这时,杆与导轨构成的回路的面积S=Ll ,回路中的感应电动势E=SΔB/ Δt + Bl v =Sk+Bl v回路的总电阻R=2Lr0回路中的感应电流i =E/R作用于杆的安培力 F =B l i解得 F=3k2 l 2 t / 2r0 ,代入数据为F=1.44×10 -3 N 例6(2000年高考科研试题) 如图所示,两根相距为d的足够长的平行金属导轨位于水平的xOy平面内,一端接有阻值为R的电阻.在x> 0 的一侧存在沿竖直方向的非均匀磁场,磁感强度B随x的增大而增大,B=kx,式中的k是一常量.一金属直杆与金属导轨垂直,可在导轨上滑动.当t=0 时位于x= 0处,速度为v0,方向沿x轴的正方向.在运动过程中,有一大小可调节的外力F作用于金属杆以保持金属杆的加速度恒定,大小为a,方向沿x轴的负方向.设除外接的电阻R外,所有其他电阻都可以忽略.问:
(1)该回路中的感应电流持续的时间多长? (2)当金属杆的速度大小为v0/2 时,回路中的感应电动势有多大?解 : (1)金属杆在导轨上先是向右做加速度为a的匀减速直线运动,到导轨右方最远处速度为零,后又沿导轨向左做加速度为a的匀加速直线运动.当过了y 轴后,由于已离开了磁场区,故回路不再有感应电流.以t1表示金属杆做匀减速运动的时间,有t1=v0/ a.从而,回路中感应电流持续的时间 T=2t1=2v0/a.(2)以x1表示金属杆的速度变为v1=v0/2 时它所在的x 坐标,由 v12=v02-2ax1,可得 x1=3v02/8a,从而,此时金属杆所在处的磁感强度 B1=kx1=3kv02/8a所以,此时回路中的感应电动势E1=B1v1d=3kv03d/16 a. 例7:水平放置的导轨处于垂直轨道平面的匀强磁场中,今从静止起用力拉金属棒ab,若拉力为恒力,经t1 秒ab的速度为v,加速度为a1 ,最终速度为2v, 若拉力的功率恒定,经t2秒ab的速度为v,加速度为a2 ,最终速度为2v, 求 a1和a2的关系解:拉力为恒力:最终有 F=F安=B2 L2 ×2v/Ra1= (F- B2 L2 v/R) / m=F/m - B2 L2 v / mR= B2 L2 v / mR拉力的功率恒定:F′= F安= P/2v = B2 L2 ×2v/R∴P/v= 4B2 L2 v/Ra2=( F2′- F安′) / m
= [P/v - B2 L2 v/R]/m= 3B2 L2 v / mRa2 = 3a1 例8、 如图示,U形导体框架的宽度L=0.5m,电阻忽略不计,其所在平面与水平面成α=30°,一根质量m=0.1kg、有效电阻R=0.5Ω的导体棒MN垂直跨放在U形框架上,离PQ的距离为b=0.2m,整个装置处于与滑轨平面正交、磁感应强度按B=0.2t2 T规律变化的磁场中,t=0时导体恰好静止,(g=10m/s2)求:
⑴ 经过多少时间导体开始滑动
⑵ 这段时间内通过导体棒横截面的电量解:⑴t=0时 B=0,恰好静止 fm =mgsin 30°=0.5NE=Δφ/ Δ t=Lb ΔB/ Δ t=0.5×0.2 ×0.4t=0.04t伏I=E/R=0.08 t 安导体开始滑动时,受力如图示BIL= fm +mgsin 30°= 1N0.2 t2×0.08 t×0.5=1t3=1/0.008 t=5秒例9、 一质量为M=1kg 的小车上固定有一质量为m = 0.2 kg ,高 l = 0.05m、电阻 R=100Ω的100匝矩形线圈,一起静止在光滑水平面上,现有一质量为m0 的子弹以v0=110m/s 的水平速度射入小车中,并随小车线圈一起进入一与线圈平面垂直,磁感强度 B=1.0T 的水平匀强磁场中如图甲所地, 小车运动过程的v-s 图象如图乙所示。求:
(1)子弹的质量m0为 。
(2)图乙中s =10cm时线圈中的电流强度I为 。
(3在进入过程中通过线圈某一截面的电量为 。
(4)求出线圈小车通过磁场的过程中线圈电阻的发热量为
。解:⑴由图象可知:进入磁场时 ,v1=10m/s由动量守恒定律m0v0 =(M+m+m0)v1 m0 =0.12kg⑵由图象可知:s=10cm v2 =8m/sE=nBLv2=100×1×0.05×8=40V I=E/R=0.4A⑶由图象可知:线圈宽度为 d=10cmq=I Δ t=n Δ Ф/R=100×1×0.1×0.05/100=5×10-3 C ⑷由图象可知:出磁场时 ,vt=2m/sQ=1/2×(M+m+m0)(v12 –vt2)=1/2×1.32×(100-4)=63.4J 思考:为什么v-s图象是三段折线?答:见备注。03年上海高考18、 (7分)图1为某一热敏电阻R(电阻值随温度的改变而改变,且对温度很敏感)的I-U关系曲线图。
⑴为了通过测量得到图1所示I-U关系的完整曲线,在图2和图3两个电路中应选择的是图 ;简要说明理由:
。(电源电动势为9V,内阻不计,滑线变阻器的阻值为0-100Ω)
⑵在图4电路中,电源电压恒为9V,电流表读数为70mA,定值电阻R1=250Ω。由热敏电阻的I-U关系曲线可知,热敏电阻两端的电压为________V;电阻R2的阻值为 Ω。
⑶举出一个可以应用热敏电阻的例子:_____________。2电压可从0V调到所需电压,调节范围较大 解: ⑵ I1=9/250=0.036A=36mA I2=34mA 由图1得 UR=5.2V 5.2 R2 =(9-5.2) / 0.034=111.8 Ω 111.6—112.0 热敏温度计 如图示, Ⅰ、 Ⅲ为两匀强磁场区,磁感应强度均为B,方向如图示,两区域中间为宽L/2的无磁场区Ⅱ,有一边长为L、粗细均匀、各边电阻为R的正方形金属框abcd置于区域Ⅰ,ab 边与磁场边界平行,现拉着金属框以速度v水平向右匀速运动,则
(1)分别求出当ab边刚进入中央无磁场区Ⅱ和进入磁场区Ⅲ时,通过ab 边的电流大小和方向.
(2)画出金属框从区域Ⅰ刚出来到完全拉入区域Ⅲ过程中水平拉力与时间的关系图象.
(3)求上述 (2)过程
中拉力所做的功04年南师大模考16解:(1)ab刚进入Ⅱ,cd边产生EE=BLv I1= BLv/4R 顺时针方向 ab刚进入Ⅲ,ab、cd边都产生E I2= 2BLv/4R 逆时针方向 (2) ab刚进入Ⅱ,F1=BI1L=B2L2v/4Rab刚进入Ⅲ,F2= 2BI2L= B2L2v/R ab进入Ⅲ,cd 还在Ⅱ,ab边产生E
F3=BI3L =BI1L =B2L2v/4R三段时间都为L/2vF-t 图象如右图示(3) W=F1L/2+ F2L/2+ F3L/2
= 3B2L3v/4R例10、如图所示,PR是一块长为L=4米的绝缘平板固定在水平地面上,整个空间有一个平行于PR的匀强电场E,在板的右半部分有一个垂直于纸面向外的匀强磁场B,一个质量为m=0.1千克、带电量为q=0.5库仑的物体,从板的P端由静止开始在电场力和摩擦力的作用下向右做匀加速运动,进入磁场后恰能做匀速运动。当物体碰到板R端挡板后被弹回,若在碰撞瞬间撤去电场,物体返回时在磁场中仍做匀速运动,离开磁场后做匀减速运动停在C点,PC=L/4,物体与平板间的动摩擦因素为μ=0.4。求:
?⑴判断物体带电性质,正电还是负电荷?
⑵物体与挡板碰撞前后的速度v1和v2;
⑶磁感强度B的大小;
⑷电场强度E的大小和方向 。解:返回时,R→D无电场力,能作匀速运动,表明无摩擦力qv2B向上,物体带正电。受力如图a 示 qv2B=mg ⑴D → C ,无磁场力, -μmg×0.25L=1/2×mv22 ⑵ P →D ,加速,E向右 (qE – μmg)×1/2L =1/2×mv12 ⑶D →R ,受力如图b 示 qE= μ(mg+ qv1B) ⑷ 解⑴⑵⑶⑷得
qv1B=2N qv2B=1N qE=1.2N
v1=5.66m/s
v2=2.83m/s
B=0.71T
E=2.4V/m 方向向右 例11、某空间存在着一个变化的电场和一个变化的磁场,如图示,电场方向由B到C,在A点,从t=1s末开始,每隔2s有一个相同的带电粒子(不计重力)沿AB方向(垂直于BC)以速度v 射出,恰好能击中C点,若AC=2BC,且粒子在AC间运动的时间小于1s。试问:
1. 图线上E和B的比值有多大?磁感应强度B 的方向如何?
2. 若第一个粒子击中C点的时刻已知为(1s+Δt ),那么第二个粒子击中C点为何时刻?解:在1s末,粒子在磁场中受洛仑兹力做匀速圆周运动,令BC=y不难得到: AC=2y, R=mv/qB=2y ∴ B=mv / 2qy在3s末,第二个粒子在电场中受电场力做类似平抛运动,∴∴E/B=4v/3第一个粒子经过t击中C点,t=1/6T=m/3qB第二个粒子击中C点经过 t 秒第二个粒子击中C点的时刻为3+ t 秒04年江苏高考12 (12分)某同学对黑箱(见图1)中一个电学元件的伏安特性进行研究.通过正确测量,他发现该元件两端的电压Uab(Uab=Ua-Ub)与流过它的电流I 之间的变化关系有如下规律
①当 - 15V < Uab < 0V 时,I 近似为零.
②当Uab≥0时,Uab和I 的实验数据见下表:(1)在图2中画出Uab≥0时该元件的伏安特性曲线.(可用铅笔作图)
(2)根据上述实验事实.该元件具有的特性是______________________。见下页单向导电性(3)若将此黑箱接入图3电路中,并在该电路的cd两端输入如图4(甲)所示的方波电压信号ucd,请在图4(乙)中定性画出负载电阻RL上的电压信号uef的波形.题目04年江苏高考13 (14分)如图所示,一个变压器(可视为理想变压器)的原线圈接在220V的市电上,向额定电压为1.80×104V的霓虹灯供电,使它正常发光.为了安全,需在原线圈回路中接入熔断器,使副线圈电路中电流超过12mA时,熔丝就熔断.
(1)熔丝的熔断电流是多大? (2)当副线圈电路中电流为10mA时.变压器的输入功率是多大?解:(1)设原、副线圈上的电压、电流分别为U1、U2、I1、I2.根据理想变压器的输入功率等于输出功率,有 I1 U1= I2U2.当I2=12 mA时,I1 即为熔断电流.代人数据,得 I1 =0.98 A (2) 设副线圈中电流为 I2 ′=10 mA时,
变压器的输入功率为P1 根据理想变压器的输入功
率等于输出功率,有P1= I2′U2代人数据,得 P1 =180 W 04年江苏高考14 (14分)如图所示的电路中,电源电动势E=6.00V,其内阻可忽略不计.电阻的阻值分别为R1=2.4 kΩ、R2=4.8kΩ,电容器的电容C=4.7μF.闭合开关S,待电流稳定后,用电压表测R1两端的电压,其稳定值为1.50V.
(1)该电压表的内阻为多大?
(2)由于电压表的接入,电容器的带电量变化了多少?解: (1)设电压表的内阻为RV,测得R1两端的电压为U1, R1与RV并联后的总电阻为R,则有 由串联电路的规律联立①②,得代入数据,可得 RV =4.8kΩ (2)电压表接入前,电容器上的电压UC等于电阻R2上的电压, R1两端的电压为UR1 ,则又接入电压表后,电容器上的电压为由于电压表的接入,电容器带电量增加了 由以上各式解得代入数据,可得 04年江苏高考17 17. (16分)汤姆生用来测定电子的比荷(电子的电荷量与质量之比)的实验装置如图所示,真空管内的阴极K发出的电子(不计初速、重力和电子间的相互作用)经加速电压加速后,穿过A'中心的小孔沿中心轴O1O的方向进入到两块水平正对放置的平行极板P和P'间的区域.当极板间不加偏转电压时,电子束打在荧光屏的中心O点处,形成了一个亮点;加上偏转电压U后,亮点偏离到O'点,(O'与O点的竖直间距为d,水平间距可忽略不计.此时,在P和P'间的区域,再加上一个方向垂直于纸面向里的匀强磁场.调节磁场的强弱,当磁感应强度的大小为B时,亮点重新回到O点.已知极板水平方向的长度为L1,极板间距为b,极板右端到荧光屏的距离为L2(如图所示). (1)求打在荧光屏O点的电子速度的大小。
(2)推导出电子的比荷的表达式 解:(1)当电子受到的电场力与洛沦兹力平衡时,电子做匀速直线运动,亮点重新回复到中心O点,设电子的速度为v,则evB=eE得 v=E/B即 v=U/Bb(2)当极板间仅有偏转电场时,电子以速度v进入后,竖直方向作匀加速运动,加速度为 a = eU / mb电子在水平方向作匀速运动,在电场内的运动时间为 t 1=L/v这样,电子在电场中,竖直向上偏转的距离为 离开电场时竖直向上的分速度为 电子离开电场后做匀速直线运动,经t2时间到达荧光屏t2=L2 /v t2时间内向上运动的距离为 这样,电子向上的总偏转距离为 可解得题目
同课章节目录
