专题09导数与方程、零点问题(第01期)-2018年高考数学备考之百强校小题精练系列(通用版)
文档属性
| 名称 | 专题09导数与方程、零点问题(第01期)-2018年高考数学备考之百强校小题精练系列(通用版) |  | |
| 格式 | zip | ||
| 文件大小 | 1000.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-11 16:41:28 | ||
图片预览




文档简介
一、单选题
1.对于函数,下列说法正确的有( )
①在处取得极大值;②有两个不同的零点;
③;④.
A. 4个 B. 3个 C. 2个 D. 1个
【答案】C
2.已知函数,若对任意的, 在上总有唯一的零点,则的取值范围是( )
A. B. C. D.
【答案】C
【解析】 函数,可得,
所以由,
当时, ,所以在上单调递减,在上单调递增,
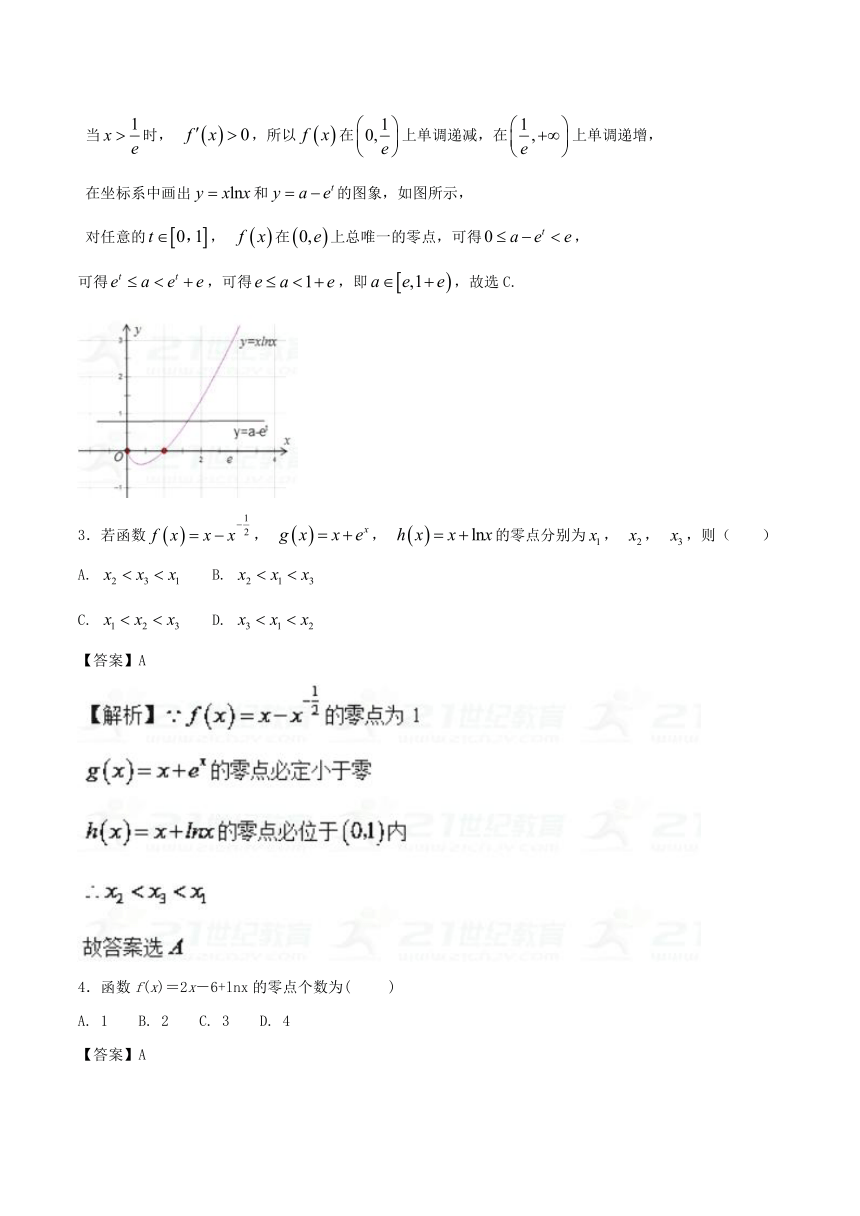
在坐标系中画出和的图象,如图所示,
对任意的, 在上总唯一的零点,可得,
可得,可得,即,故选C.
3.若函数, , 的零点分别为, , ,则( )
A. B.
C. D.
【答案】A
4.函数f(x)=2x-6+lnx的零点个数为( )
A. 1 B. 2 C. 3 D. 4
【答案】A
【解析】,所以函数在上递增,又,所以函数的零点只有1个
故选A
5.已知函数(是以为底的自然对数, ),若存 在实数,满足,则的取值范围为
A. B.
C. D.
【答案】C
当时, ,即在上为减函数;当时, ,即在上为增函数.
∴
∵
∴
∴的取值范围为
故选C.
6.若函数在区间内有两个不同的零点,则实数的取值范围为( )
A. B. C. D.
【答案】D
7.函数,方程有4个不想等实根,则的取值范围是( )
A. B. C. D.
【答案】C
【解析】根据题意画出函数图像:
设 有两个根,每个t值对应两个x值,故情况为
当属于情况一时,将0代入方程得到m=1,此时二次方程的根是确定的一个为0,一个为2,不符合题意;
当属于情况二时,
故答案为:C.
8.已知, ,若存在,使得,则称函数与互为“度零点函数”.若与互为“1度零点函数”,则实数的取值范围为( )
A. B. C. D.
【答案】B
9.已知三次函数, ,且有三个零点.若三次函数和均为上的单调函数,且这两个函数的导函数均有零点,则零点的个数为( )
A. 个 B. 个 C. 个 D. 个或个
【答案】A
10.已知关于的不等式存在唯一的整数解,则实数的取值范围是( )
A. B. C. D.
【答案】A
【解析】不等式即 设 则在上单调递减,在上单调递增, 的图像如图所示,,由图可知, 且不等式有唯一的整数解2,设 则
故选A。
11.已知当时,关于的方程有唯一实数解,则值所在的范围是( )
A. B. C. D.
【答案】B
12.已知函数在区间上有两个不同的零点,则实数的取值范围为
A. B. C. D.
【答案】A
【解析】令,则,依题意与在区间上有两个不同的交点,也即图像有两个不同的交点. ,故在上递增,在上递减,且, ,由于,故的最小值为,直到与图像相切时,观察选项可知,只有选项正确.
二、填空题
13.若函数有三个不同的零点,则实数的取值范围是___________.
【答案】
14.已知y=f (x)为R上的可导函数,当x≠0时,f′(x)+>0,若g(x)=f (x)+,则函数g(x)的零点个数为________.
【答案】0
【解析】令h(x)=xf (x),因为当x≠0时, >0,所以>0,因此当x>0时,h′(x)>0,当x<0时, h′(x)<0,又h(0)=0,易知当x≠0时,h(x)>0,又g(x)=,所以g(x)≠0,故函数g(x)的零点个数为0.
故答案为:0
15.已知函数 (其中为自然对数的底数),曲线上存在不同的两点, 使得曲线在这两点处的切线都与轴垂直,则实数的取值范围是__________.
【答案】
16.关于的方程有两个不等实根,则实数的取值范围是__________.
【答案】
【解析】由得
1.对于函数,下列说法正确的有( )
①在处取得极大值;②有两个不同的零点;
③;④.
A. 4个 B. 3个 C. 2个 D. 1个
【答案】C
2.已知函数,若对任意的, 在上总有唯一的零点,则的取值范围是( )
A. B. C. D.
【答案】C
【解析】 函数,可得,
所以由,
当时, ,所以在上单调递减,在上单调递增,
在坐标系中画出和的图象,如图所示,
对任意的, 在上总唯一的零点,可得,
可得,可得,即,故选C.
3.若函数, , 的零点分别为, , ,则( )
A. B.
C. D.
【答案】A
4.函数f(x)=2x-6+lnx的零点个数为( )
A. 1 B. 2 C. 3 D. 4
【答案】A
【解析】,所以函数在上递增,又,所以函数的零点只有1个
故选A
5.已知函数(是以为底的自然对数, ),若存 在实数,满足,则的取值范围为
A. B.
C. D.
【答案】C
当时, ,即在上为减函数;当时, ,即在上为增函数.
∴
∵
∴
∴的取值范围为
故选C.
6.若函数在区间内有两个不同的零点,则实数的取值范围为( )
A. B. C. D.
【答案】D
7.函数,方程有4个不想等实根,则的取值范围是( )
A. B. C. D.
【答案】C
【解析】根据题意画出函数图像:
设 有两个根,每个t值对应两个x值,故情况为
当属于情况一时,将0代入方程得到m=1,此时二次方程的根是确定的一个为0,一个为2,不符合题意;
当属于情况二时,
故答案为:C.
8.已知, ,若存在,使得,则称函数与互为“度零点函数”.若与互为“1度零点函数”,则实数的取值范围为( )
A. B. C. D.
【答案】B
9.已知三次函数, ,且有三个零点.若三次函数和均为上的单调函数,且这两个函数的导函数均有零点,则零点的个数为( )
A. 个 B. 个 C. 个 D. 个或个
【答案】A
10.已知关于的不等式存在唯一的整数解,则实数的取值范围是( )
A. B. C. D.
【答案】A
【解析】不等式即 设 则在上单调递减,在上单调递增, 的图像如图所示,,由图可知, 且不等式有唯一的整数解2,设 则
故选A。
11.已知当时,关于的方程有唯一实数解,则值所在的范围是( )
A. B. C. D.
【答案】B
12.已知函数在区间上有两个不同的零点,则实数的取值范围为
A. B. C. D.
【答案】A
【解析】令,则,依题意与在区间上有两个不同的交点,也即图像有两个不同的交点. ,故在上递增,在上递减,且, ,由于,故的最小值为,直到与图像相切时,观察选项可知,只有选项正确.
二、填空题
13.若函数有三个不同的零点,则实数的取值范围是___________.
【答案】
14.已知y=f (x)为R上的可导函数,当x≠0时,f′(x)+>0,若g(x)=f (x)+,则函数g(x)的零点个数为________.
【答案】0
【解析】令h(x)=xf (x),因为当x≠0时, >0,所以>0,因此当x>0时,h′(x)>0,当x<0时, h′(x)<0,又h(0)=0,易知当x≠0时,h(x)>0,又g(x)=,所以g(x)≠0,故函数g(x)的零点个数为0.
故答案为:0
15.已知函数 (其中为自然对数的底数),曲线上存在不同的两点, 使得曲线在这两点处的切线都与轴垂直,则实数的取值范围是__________.
【答案】
16.关于的方程有两个不等实根,则实数的取值范围是__________.
【答案】
【解析】由得
同课章节目录
