9.3 平行四边形(1) 课件(共25张PPT)
文档属性
| 名称 | 9.3 平行四边形(1) 课件(共25张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 613.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-11 20:58:10 | ||
图片预览




文档简介
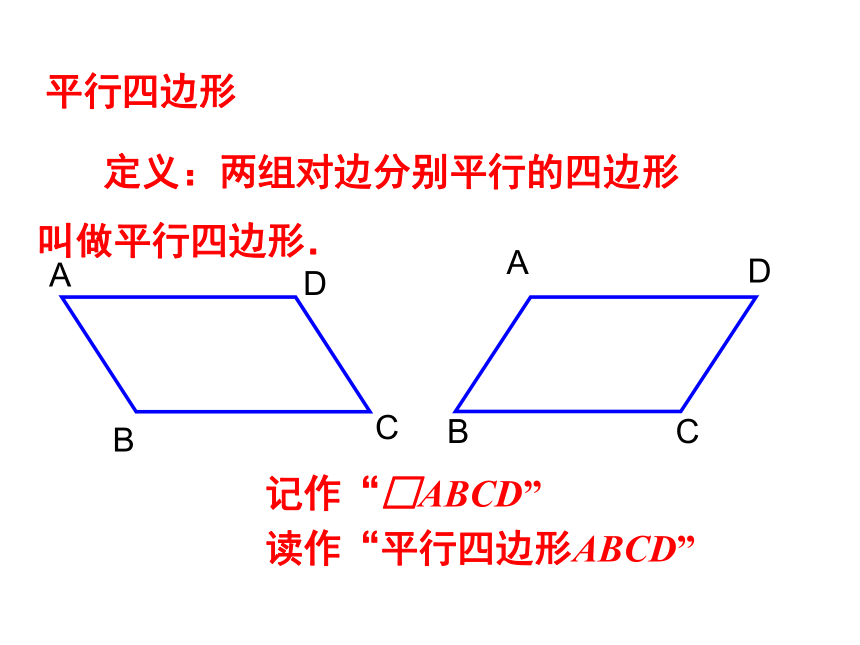
课件25张PPT。9.3 平行四边形(1)仔细看一看上面的图片中有你熟悉的图形吗? 定义:两组对边分别平行的四边形
叫做平行四边形.平行四边形记作“□ABCD”读作“平行四边形ABCD”ABCDABCD画一画ABCDO· 如图,O是△ABC的边AC上的中点,画出△ABC关于点O成中心对称的图形. 四边形ABCD是中心对称图形,
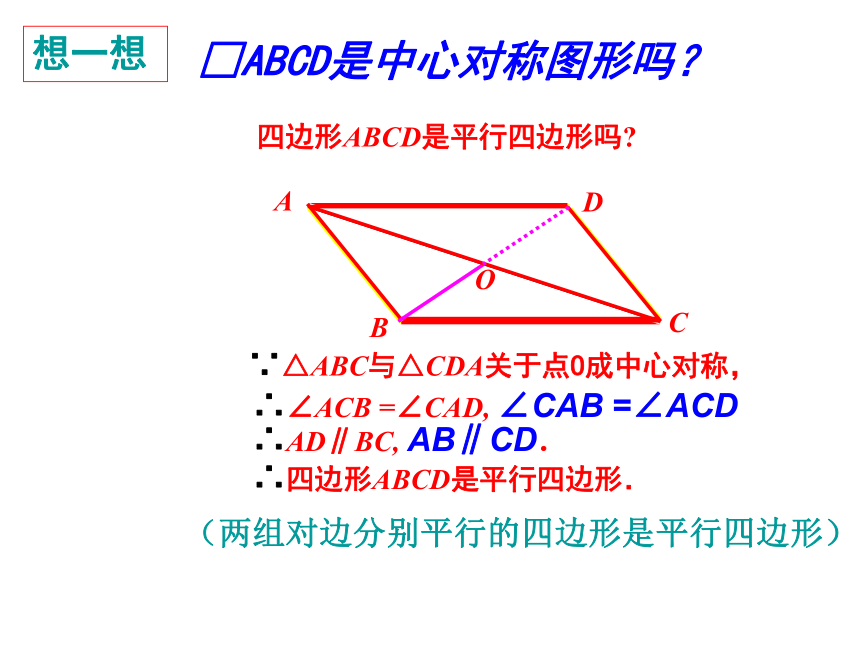
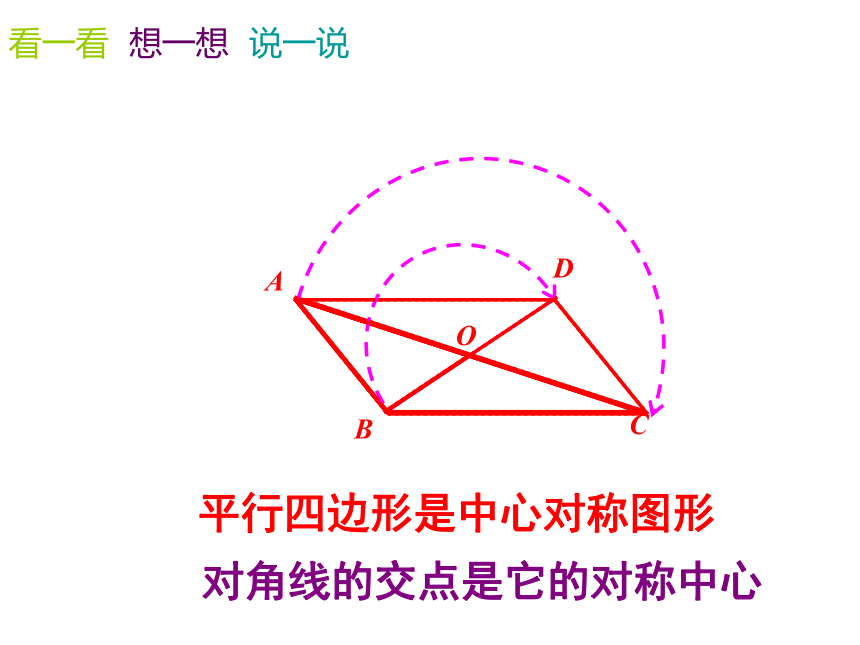
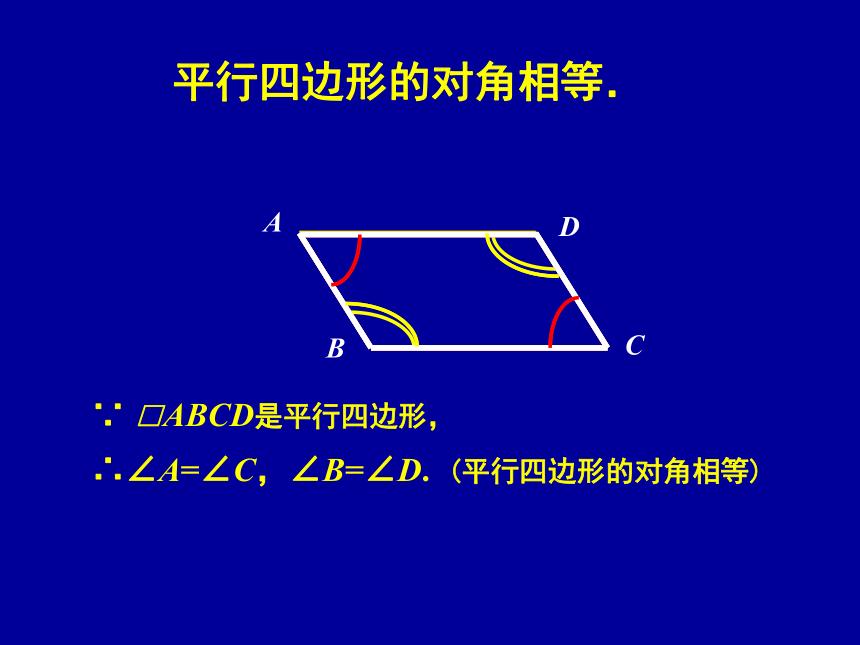
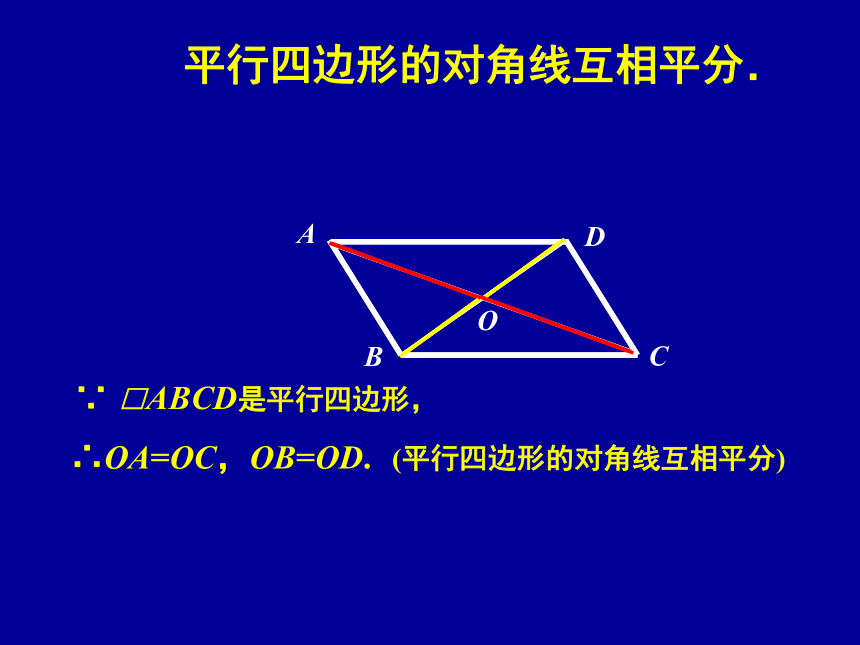
点O是它的对称中心. 四边形ABCD是中心对称图形吗?想一想DO四边形ABCD是平行四边形吗?∵△ABC与△CDA关于点O成中心对称,∴∠ACB =∠CAD, ∠CAB =∠ACD∴AD∥BC, AB∥CD.∴四边形ABCD是平行四边形.(两组对边分别平行的四边形是平行四边形)□ABCD是中心对称图形吗?DOBAC平行四边形是中心对称图形看一看 想一想 说一说对角线的交点是它的对称中心DO平行四边形的对边相等.∵四边形ABCD是平行四边形,∴AB=CD,AD=BC.(平行四边形的对边相等)DABC平行四边形的对角相等. ∵ □ABCD是平行四边形,∴∠A=∠C,∠B=∠D.(平行四边形的对角相等) DABCO平行四边形的对角线互相平分. ∴OA=OC,OB=OD.(平行四边形的对角线互相平分) ∵ □ABCD是平行四边形,平行四边形的性质: (1)平行四边形是中心对称图形. (2)平行四边形的对边相等; (3)平行四边形的对角相等; (4)平行四边形的对角线互相平分. 平行四边形的邻角互补. 平行四边形的对边平行. ADBC 平行四边形的对边相等,对角相等,对角线互相平分. (1)□ABCD中,若∠A=55°,则∠B=____; ∠C=____; ∠D=____;例1 填空:108°26 cm55°125°125°ABCD (2)已知平行四边形的相邻两角的度数之比为2∶3,则较大的角为_____; (3) 已知□ ABCD中, AB=5 cm, BC=8 cm,则四边形ABCD的周长=_____
例2 如图,A′B′∥AB,B′C′∥BC,C′A′∥CA,图中有几个平行四边形?将
它们表示出来,并说明理由. 解:图中共有3个平行四边形:□ABCB′ 、□ACBC′、
□CABA′ .例题探究 ∵A′B′∥AB,B′C′∥BC,
∴四边形ABCB′是平行四边形.
(两组对边分别平行的四边形是平行四边形.)同理可得:四边形ACBC′和四边形CABA′都是平行四边形。 如图,A′B′∥AB,B′C′∥BC,C′A′∥CA,从中你还能得到哪些结论?例题拓展(1)图中点A是边C′B′
的中点吗?
∠ABC =∠B′,∠BAC =∠A′, ∠ACB =∠C′;AC′= BC = AB′ ,点A是B′C′的中点。BC′= AC = BA′,点B是C′A′ 的中点。CA′= AB = CB′,点C是A′B′ 的中点。平行四边形的对角相等平行四边形的对边相等 学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里呢?例题拓展(2)ABC 1. 如图, □ ABCD中,
(1)若 ∠A+∠C =200°,
求∠B的度数.解:(1)细心练一练∴ ∠A=∠C ∵ ∠A+∠C =200°∴ ∠A=∠C= 100°∵ □ ABCD(平行四边形的对角相等) (已知)∴AD∥BC∴ ∠A+∠B =180°∴ ∠B =180°- ∠A= 180°- 100°= 80°(已知)(已知)(平行四边形的定义) (两直线平行,同旁内角互补) ∵ □ ABCD答案:AD= 4.5 cm.细心练一练 1. 如图, □ ABCD中,
(2) 已知□ ABCD的周长是18 cm, AB=3.5 cm, 求AD的长。可以得到:
□ ABCD的相邻两边之和为9 2.如图, □ ABCD的对角线相交于点O. (1)图中有几对全等三角形?解: (1) 图中有4对全等三角形.细心练一练 (2)BC=7 cm,BD=10 cm,AC=6 cm.求△AOD的周长. 2.如图, □ ABCD的对角线相交于点O.答案:15 cm.细心练一练 (1)图中有几对全等三角形?735 (3) □ ABCD的周长18 cm, BC - AB=3 cm,求AB、BC的长. 2.如图, □ ABCD的对角线相交于点O.可以得到AB+BC=9 ,细心练一练 (1)图中有几对全等三角形? (2)BC=7 cm,BD=10 cm,AC=6 cm.求△AOD的周长.可以解得:又因为 BC-AB=3 ,解(3):由□ABCD 周长为18 cm,AB=3 cm ,B C=6 cm。 (3) □ ABCD的周长18 cm, BC - AB=3 cm,求AB、BC的长. 2.如图, □ ABCD的对角线相交于点O. ∴ BC +AB=9 细心练一练 (1)图中有几对全等三角形? (2)BC=7 cm,BD=10 cm,AC=6 cm.求△AOD的周长. (4) □ ABCD的周长18 cm,△AOB的周长比△COB的周长少3 cm,求AB、BC的长.∴(OB+OC+BC) - (OB+OA+AB)=3解得:AB=3 cm ,BC=6 cm。即 BC- AB=3 ∵ △AOB的周长比△COB的周长少3 cm∴OA=OC(平行四边形的对角线互相平分) BC +AB=9 解:(4) ∵ □ ABCD的周长为18 cm∵ □ ABCDAEDCB3.如图, □ABCD中,AB=6,BC=10,
BE平分∠ABC交AD于点E,求 DE的长。123AEDCB3.如图, □ABCD中,AB=6,BC=10,
BE平分∠ABC交AD于点E,求 DE的长。123一题多变如果CF平分∠BCD交AD于点F,你能求出EF的长吗?
试试看!F44此题中的AF与DE一定相等吗?收获园 1. 本节课我们学习了平行四边形,知道了两组对边分别平行的四边形是平行四边形.它既可以用来判定一个四边形是平行四边形,也是平行四边形最基本的一个性质. 2. 平行四边形的性质:
(1)平行四边形的对边平行且相等.
(2)平行四边形的对角相等.
(3)平行四边形的对角线互相平分.
(4)平行四边形是中心对称图形.收获园预习作业:1.预习课本P 87-88;完成P87的操作
2.完成课本P88T1,P90T2;
3.同步导学: 3.4(2)新知导读课堂作业:补充习题3.4(1)课后作业:同步导学:3.4(1)的随堂演练T1,2,3,4谢谢各位领导、专家、同行莅临指导
叫做平行四边形.平行四边形记作“□ABCD”读作“平行四边形ABCD”ABCDABCD画一画ABCDO· 如图,O是△ABC的边AC上的中点,画出△ABC关于点O成中心对称的图形. 四边形ABCD是中心对称图形,
点O是它的对称中心. 四边形ABCD是中心对称图形吗?想一想DO四边形ABCD是平行四边形吗?∵△ABC与△CDA关于点O成中心对称,∴∠ACB =∠CAD, ∠CAB =∠ACD∴AD∥BC, AB∥CD.∴四边形ABCD是平行四边形.(两组对边分别平行的四边形是平行四边形)□ABCD是中心对称图形吗?DOBAC平行四边形是中心对称图形看一看 想一想 说一说对角线的交点是它的对称中心DO平行四边形的对边相等.∵四边形ABCD是平行四边形,∴AB=CD,AD=BC.(平行四边形的对边相等)DABC平行四边形的对角相等. ∵ □ABCD是平行四边形,∴∠A=∠C,∠B=∠D.(平行四边形的对角相等) DABCO平行四边形的对角线互相平分. ∴OA=OC,OB=OD.(平行四边形的对角线互相平分) ∵ □ABCD是平行四边形,平行四边形的性质: (1)平行四边形是中心对称图形. (2)平行四边形的对边相等; (3)平行四边形的对角相等; (4)平行四边形的对角线互相平分. 平行四边形的邻角互补. 平行四边形的对边平行. ADBC 平行四边形的对边相等,对角相等,对角线互相平分. (1)□ABCD中,若∠A=55°,则∠B=____; ∠C=____; ∠D=____;例1 填空:108°26 cm55°125°125°ABCD (2)已知平行四边形的相邻两角的度数之比为2∶3,则较大的角为_____; (3) 已知□ ABCD中, AB=5 cm, BC=8 cm,则四边形ABCD的周长=_____
例2 如图,A′B′∥AB,B′C′∥BC,C′A′∥CA,图中有几个平行四边形?将
它们表示出来,并说明理由. 解:图中共有3个平行四边形:□ABCB′ 、□ACBC′、
□CABA′ .例题探究 ∵A′B′∥AB,B′C′∥BC,
∴四边形ABCB′是平行四边形.
(两组对边分别平行的四边形是平行四边形.)同理可得:四边形ACBC′和四边形CABA′都是平行四边形。 如图,A′B′∥AB,B′C′∥BC,C′A′∥CA,从中你还能得到哪些结论?例题拓展(1)图中点A是边C′B′
的中点吗?
∠ABC =∠B′,∠BAC =∠A′, ∠ACB =∠C′;AC′= BC = AB′ ,点A是B′C′的中点。BC′= AC = BA′,点B是C′A′ 的中点。CA′= AB = CB′,点C是A′B′ 的中点。平行四边形的对角相等平行四边形的对边相等 学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里呢?例题拓展(2)ABC 1. 如图, □ ABCD中,
(1)若 ∠A+∠C =200°,
求∠B的度数.解:(1)细心练一练∴ ∠A=∠C ∵ ∠A+∠C =200°∴ ∠A=∠C= 100°∵ □ ABCD(平行四边形的对角相等) (已知)∴AD∥BC∴ ∠A+∠B =180°∴ ∠B =180°- ∠A= 180°- 100°= 80°(已知)(已知)(平行四边形的定义) (两直线平行,同旁内角互补) ∵ □ ABCD答案:AD= 4.5 cm.细心练一练 1. 如图, □ ABCD中,
(2) 已知□ ABCD的周长是18 cm, AB=3.5 cm, 求AD的长。可以得到:
□ ABCD的相邻两边之和为9 2.如图, □ ABCD的对角线相交于点O. (1)图中有几对全等三角形?解: (1) 图中有4对全等三角形.细心练一练 (2)BC=7 cm,BD=10 cm,AC=6 cm.求△AOD的周长. 2.如图, □ ABCD的对角线相交于点O.答案:15 cm.细心练一练 (1)图中有几对全等三角形?735 (3) □ ABCD的周长18 cm, BC - AB=3 cm,求AB、BC的长. 2.如图, □ ABCD的对角线相交于点O.可以得到AB+BC=9 ,细心练一练 (1)图中有几对全等三角形? (2)BC=7 cm,BD=10 cm,AC=6 cm.求△AOD的周长.可以解得:又因为 BC-AB=3 ,解(3):由□ABCD 周长为18 cm,AB=3 cm ,B C=6 cm。 (3) □ ABCD的周长18 cm, BC - AB=3 cm,求AB、BC的长. 2.如图, □ ABCD的对角线相交于点O. ∴ BC +AB=9 细心练一练 (1)图中有几对全等三角形? (2)BC=7 cm,BD=10 cm,AC=6 cm.求△AOD的周长. (4) □ ABCD的周长18 cm,△AOB的周长比△COB的周长少3 cm,求AB、BC的长.∴(OB+OC+BC) - (OB+OA+AB)=3解得:AB=3 cm ,BC=6 cm。即 BC- AB=3 ∵ △AOB的周长比△COB的周长少3 cm∴OA=OC(平行四边形的对角线互相平分) BC +AB=9 解:(4) ∵ □ ABCD的周长为18 cm∵ □ ABCDAEDCB3.如图, □ABCD中,AB=6,BC=10,
BE平分∠ABC交AD于点E,求 DE的长。123AEDCB3.如图, □ABCD中,AB=6,BC=10,
BE平分∠ABC交AD于点E,求 DE的长。123一题多变如果CF平分∠BCD交AD于点F,你能求出EF的长吗?
试试看!F44此题中的AF与DE一定相等吗?收获园 1. 本节课我们学习了平行四边形,知道了两组对边分别平行的四边形是平行四边形.它既可以用来判定一个四边形是平行四边形,也是平行四边形最基本的一个性质. 2. 平行四边形的性质:
(1)平行四边形的对边平行且相等.
(2)平行四边形的对角相等.
(3)平行四边形的对角线互相平分.
(4)平行四边形是中心对称图形.收获园预习作业:1.预习课本P 87-88;完成P87的操作
2.完成课本P88T1,P90T2;
3.同步导学: 3.4(2)新知导读课堂作业:补充习题3.4(1)课后作业:同步导学:3.4(1)的随堂演练T1,2,3,4谢谢各位领导、专家、同行莅临指导
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
