6.1.2 中位数同步练习
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
6.1.2 中位数同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.把一组数据按从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,那么位于中间的数称为这组数据的中位数;如果数据的个数是偶数,那么位于中间的两个数的平均数称为这组数据的中位数.
2.中位数把一组数据分成相同数目的两部分,其中一部分都小于或等于中位数,而另一部分都大于或等于中位数,因此,中位数常用来描述“中间位置”或“中等水平”,但中位数没有利用数据组中所有的信息.
基础知识和能力拓展精练
1 、选择题
一组数据1,8,4,2,2,5的中位数是( )
A. 2 B. 3 C. 4 D. 5
假设五个相异正整数的平均数是15,中位数是18,则这五个相异正整数中的最大数的最大值为( )
A. 24 B. 32 C. 35 D. 40
根据下表中的信息解决问题:
若该组数据的中位数不大于38,则符合条件的正数的取值共有( )
A. 3个 B. 4个 C. 5个 D. 6个
已知八年级(4)班全班35人身高的平均数与中位数都是150cm,但后来发现其中有一位同学的身高登记错误,误将160cm写成166cm,正确的平均数为a cm,中位数为b cm,关于平均数a的叙述,下列正确的是( )
A.大于158 B.小于158 C.等于158 D.无法确定
贵阳市“阳光小区”开展“节约用水,从我做起”的活动,一个月后,社区居委会从小区住户中抽取10个家庭与他们上个月的用水量进行比较,统计出节水情况如表:
节水量(m3) 0.3 0.4 0.5 0.6 0.7
家庭数(个) 2 2 4 1 1
那么这10个家庭的节水量(m3)的平均数和中位数分别是( )
A.0.47和0.5 B.0.5和0.5 C.0.47和4 D.0.5和4
如表为初三(1)班全部43名同学某次数学测验成绩的统计结果,则下列说法正确的是( )
成绩(分) 70 80 90
男生(人) 5 10 7
女生(人) 4 13 4
A.男生的平均成绩大于女生的平均成绩
B.男生的平均成绩小于女生的平均成绩
C.男生成绩的中位数大于女生成绩的中位数
D.男生成绩的中位数小于女生成绩的中位数
某班组织了一次读书活动,统计了10名同学在一周内的读书时间,他们一周内的读书时间累计如表,则这10名同学一周内累计读书时间的中位数是( )
一周内累计的读书时间(小时) 5 8 10 14
人数(个) 1 4 3 2
A.8 B. 7 C. 9 D. 10
某班50名学生期末考试数学成绩(单位:分)的频率分布直方图如图所示,其中
数据不在分点上,对图中提供的信息作出如下的判断:
(1)成绩在49.5分~59.5分段的人数与89.5分~100分段的人数相等;
(2)成绩在79.5~89.5分段的人数占30%;
(3)成绩在79.5分以上的学生有20人;
(4)本次考试成绩的中位数落在69.5~79.5分段内.
其中正确的判断有( )
A.4个 B.3个 C.2个 D.1个
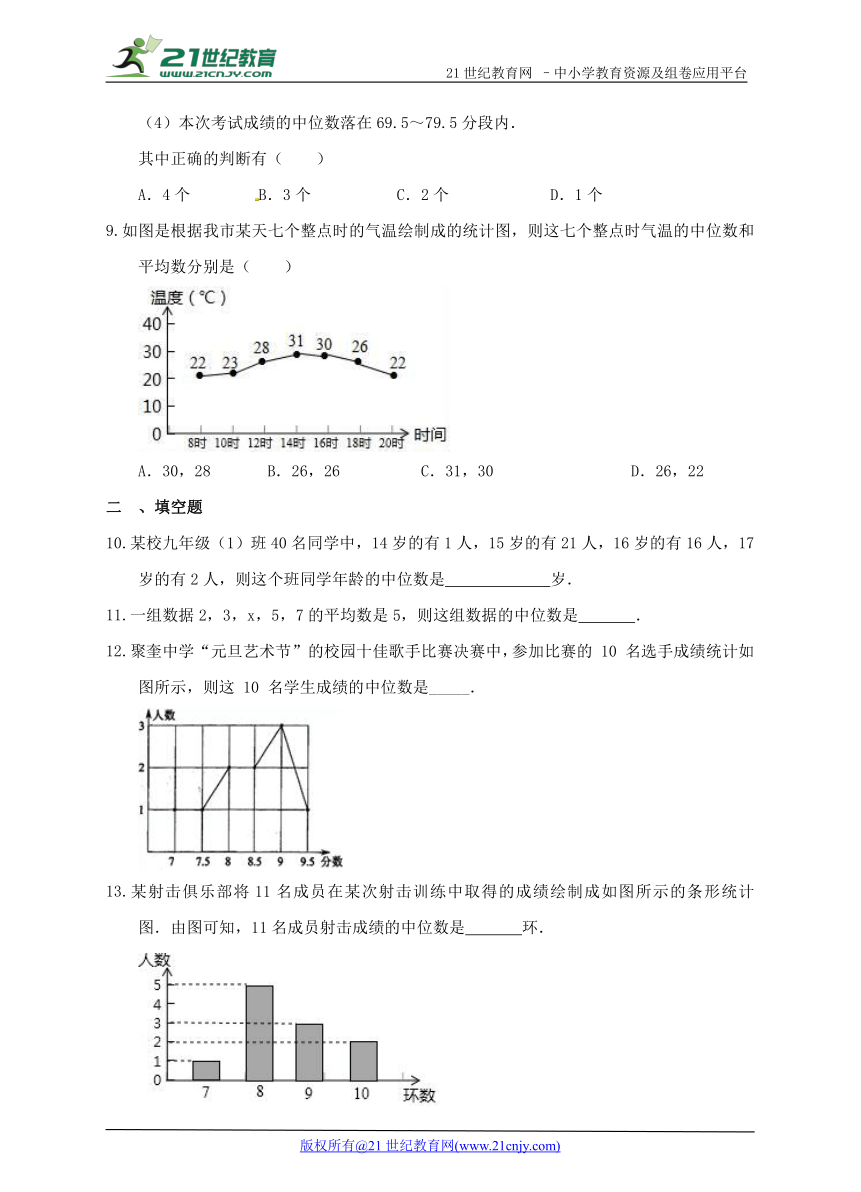
如图是根据我市某天七个整点时的气温绘制成的统计图,则这七个整点时气温的中位数和平均数分别是( )
A.30,28 B.26,26 C.31,30 D.26,22
2 、填空题
某校九年级(1)班40名同学中,14岁的有1人,15岁的有21人,16岁的有16人,17岁的有2人,则这个班同学年龄的中位数是 岁.
一组数据2,3,x,5,7的平均数是5,则这组数据的中位数是 .
聚奎中学“元旦艺术节”的校园十佳歌手比赛决赛中,参加比赛的 10 名选手成绩统计如图所示,则这 10 名学生成绩的中位数是_____.
某射击俱乐部将11名成员在某次射击训练中取得的成绩绘制成如图所示的条形统计图.由图可知,11名成员射击成绩的中位数是 环.
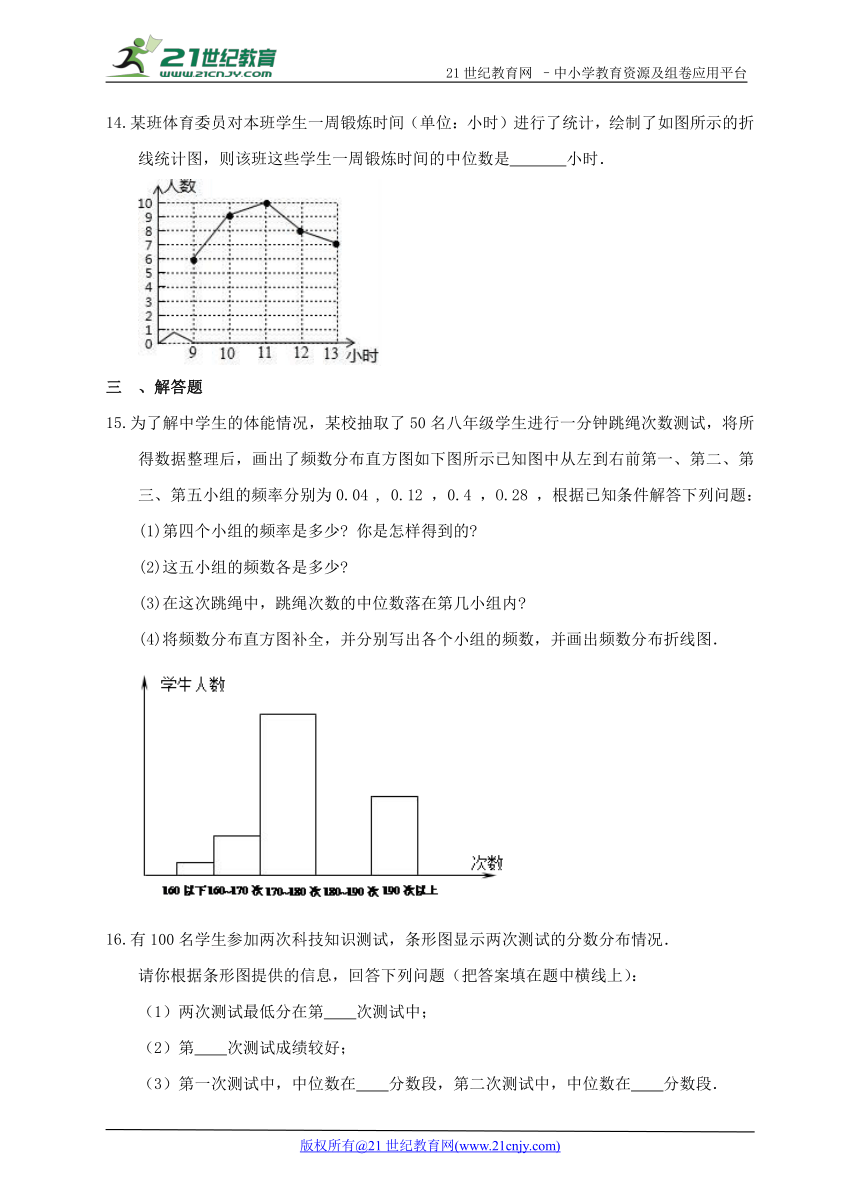
某班体育委员对本班学生一周锻炼时间(单位:小时)进行了统计,绘制了如图所示的折线统计图,则该班这些学生一周锻炼时间的中位数是 小时.
3 、解答题
为了解中学生的体能情况,某校抽取了50名八年级学生进行一分钟跳绳次数测试,将所得数据整理后,画出了频数分布直方图如下图所示已知图中从左到右前第一、第二、第三、第五小组的频率分别为0.04 , 0.12 ,0.4 ,O.28 ,根据已知条件解答下列问题:
(1)第四个小组的频率是多少 你是怎样得到的
(2)这五小组的频数各是多少
(3)在这次跳绳中,跳绳次数的中位数落在第几小组内
(4)将频数分布直方图补全,并分别写出各个小组的频数,并画出频数分布折线图.
有100名学生参加两次科技知识测试,条形图显示两次测试的分数分布情况.
请你根据条形图提供的信息,回答下列问题(把答案填在题中横线上):
(1)两次测试最低分在第 次测试中;
(2)第 次测试成绩较好;
(3)第一次测试中,中位数在 分数段,第二次测试中,中位数在 分数段.
国家规定,“中小学生每天在校体育锻炼时间不小于1小时”,某地区就“每天在校体育锻炼时间”的问题随机调查了若干名中学生,根据调查结果制作如下统计图(不完整).其中分组情况:A组:时间小于0.5小时;B组:时间大于等于0.5小时且小于1小时;C组:时间大于等于1小时且小于1.5小时;D组:时间大于等于1.5小时.
根据以上信息,回答下列问题:
(1)A组的人数是 人,并补全条形统计图;
(2)本次调查数据的中位数落在组 ;
(3)根据统计数据估计该地区25000名中学生中,达到国家规定的每天在校体育锻炼时间的人数约有多少人.
某商场对A.B两款运动鞋的销售情况进行了为期5天的统计,得到了这两款运动鞋每天的销售量及总销售额统计图(如图所示).已知第4天B款运动鞋的销售量是A款的.
(1)求第4天B款运动鞋的销售量.
(2)这5天期间,B款运动鞋每天销售量的平均数和中位数分别是多少?
(3)若在这5天期间两款运动鞋的销售单价保持不变,求第3天的总销售额(销售额=销售单价×销售量).
在一次社会调查活动中,小李收集到某“健步走运动”团队20名成员一天行走的步数,记录如下:
5640 6430 6520 6798 7325
8430 8215 7453 7446 6754
7638 6834 7326 6830 8648
8753 9450 9865 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下不完整的统计图表,步数分布统计图.
组别 步数分组 频数
A 5500≤x<6500 m
B 6500≤x<7500 10
C 7500≤x<8500 4
D 8500≤x<9500 n
E 9500≤x<10500 1
根据以上信息解答下列问题:
(1)填空:m= ,n= ;
(2)请补全条形统计图;
(3)这20名“健步走运动”团队成员一天行走的步数的中位数落在 组;
(4)若该团队共有200人,请估计其中一天行走步数少于8500步的人数.
答案解析
1 、选择题
B
【解析】将数据重新排列得:1、2、2、4、5、8,
则其中位数为 =3,
故选:B.
C
【解析】要使最大值最大,就要使其他的4个数尽量小,
设最大值为x,
∵五个相异正整数的平均数是15,中位数是18,
∴五个相异正整数的和是75,有两个比18小,两个比18大,
∴满足条件的五个数为:1, 2 ,18, 19, x,
∴x=75-19-1-2-18=35,
故选C.
C
【解析】解:当a=1时,有19个数据,最中间是:第10个数据,则中位数是38;
当a=2时,有20个数据,最中间是:第10和11个数据,则中位数是38;
当a=3时,有21个数据,最中间是:第11个数据,则中位数是38;
当a=4时,有22个数据,最中间是:第11和12个数据,则中位数是38;
当a=5时,有23个数据,最中间是:第12个数据,则中位数是38;
当a=6时,有24个数据,最中间是:第12和13个数据,则中位数是38.5;
故该组数据的中位数不大于38,则符合条件的正整数a的取值共有:5个.
故选C.
B
【解析】已知在错误登记中全班35人身高的平均数是150cm,则总身高总和为35×150=5250;修改后,减少了6厘米,为5244厘米,则正确的平均数为a=厘米,小于158cm.故选B.
【分析】找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数;平均数是指在一组数据中所有数据之和再除以数据的个数.
解:这10个数据的平均数为=0.47,
中位数为=0.5,
故选:A
【分析】根据平均数的定义分别求出男生与女生的平均成绩,再根据中位数的定义分别求出男生与女生成绩的中位数即可求解.
解:∵男生的平均成绩是:(70×5+80×10+90×7)÷22=1780÷22=80,
女生的平均成绩是:(70×4+80×13+90×4)÷21=1680÷21=80,
∴男生的平均成绩大于女生的平均成绩.
∵男生一共22人,位于中间的两个数都是80,所以中位数是(80+80)÷2=80,
女生一共21人,位于最中间的一个数是80,所以中位数是80,
∴男生成绩的中位数等于女生成绩的中位数.
故选A.
分析:根据中位数的概念求解.
解答: 解:∵共有10名同学,
∴第5名和第6名同学的读书时间的平均数为中位数,
则中位数为:=9.
故选C.
点评:本题考查了中位数的知识,将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
分析:根据频数分布直方图的特点,以及中位数的定义进行解答.
解:(1)从频率分布直方图上看成绩在49.5分~59.5分段的人数与89.5分~100分段的人数相等,故选项正确;
(2)从频率分布直方图上看出:成绩在79.5~89.5分段的人数30%,故选项正确;
(3)成绩在79.5分以上的学生有50×(30%+10%)=20人,故选项正确;
(4)将该组数据按从小到大(或按从大到小)的顺序排列,本次考试成绩的中位数落在69.5~79.5分段内,故选项正确.
故选A.
【分析】此题根据中位数,平均数的定义解答.
解:由图可知,把7个数据从小到大排列为22,22,23,26,28,30,31,中位数是第4位数,第4位是26,所以中位数是26.
平均数是(22×2+23+26+28+30+31)÷7=26,所以平均数是26.
故选:B.
2 、填空题
分析: 根据中位数的定义找出第20和21个数的平均数,即可得出答案.
解答: 解:∵该班有40名同学,
∴这个班同学年龄的中位数是第20和21个数的平均数,
∵15岁的有21人,
∴这个班同学年龄的中位数是15岁;
故答案为:15.
点评: 此题考查了中位数,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),熟练掌握中位数的定义是本题的关键.
【分析】求出x的值,然后将数据按照从小到大依次排列即可求出中位数.
解:x=5×5﹣2﹣3﹣5﹣7=8,
这组数据为2,3,5,7,8,
故中位数为5.
8.5
【解析】分析:根据中位数的定义找出最中间的两个数,再求出它们的平均数即可.
详解:∵共有10名学生,
∴这10名学生成绩的中位数是第5和6个数的平均数,
∵第5和6个数分别是:8.5,8.5,
∴10名学生成绩的中位数是(8.5+8.5)÷2=8.5;
故答案为:8.5.
点睛:此题考查了中位数,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.
【分析】11名成员射击成绩处在第6位的是8,则中位数为8.
解:∵按大小排列在中间的射击成绩为8环,则中位数为8.
故答案为:8.
【分析】根据统计图中的数据可以得到一共多少人,然后根据中位数的定义即可求得这组数据的中位数.
解:由统计图可知,
一共有:6+9+10+8+7=40(人),
∴该班这些学生一周锻炼时间的中位数是第20个和21个学生对应的数据的平均数,
∴该班这些学生一周锻炼时间的中位数是11,
故答案为:11.
3 、解答题
答案见解析
【解析】试题分析:(1)用1减去其余四组的频率即可;
(2)利用频数=频率乘总数得到;
(3)中位数是第25个同学、第26个同学跳绳次数之和的一半;
(4)依数画图即可.
试题解析:解:(1)由1减去已知4个小组的频率之和得到结果,第四个小组的频率=1﹣(0.04+0.12+0.4+0.28)=0.16;
(2)由频率=,且知各小组的频率分别为0.04,0.12,0.4,0.16,0.28及总人数为50,故有50×0.04=2,50×0.12=6,50×0.4=20,50×0.16=8,50×0.28=14,从而可知前5个小组的频数分别为2,6,20,8,14;
(3)由中位数应是第25个同学、第26个同学跳绳次数之和的一半.
由频数分布直方图可知,第25个同学、第26个同学跳绳次数均落在第三个小组内.
故而可知在这次测试中,跳绳次数的中位数落在第三小组内;
(4)由于第四小组的频数为8,第一小组频数为2,故第四小组的小长方形的高应是第一小组小长方形的高的4倍.
点睛:本题考查了读频数分布直方图的能力和利用统计图获取信息的能力.也考查了频率和中位数的概念.
(1)一;(2)二;(3)20﹣39;40﹣59.
【解析】试题分析:(1)由统计图直接得到;
(2)看统计图判断;
(3)中位数是将数据从小到大排列,取中间两个数的平均数.
试题解析:解:(1)两次测试最低分在第一次测试中;
(2)第一次测试的低分较多,高分较少,所以第二次的测试成绩较好;
(3)取第50名与51名同学成绩的平均数,所以第一次测试中,中位数落在20﹣39分数段;第二次测试中,中位数落在40﹣59分数段.
(1)50,补图见解析;(2)C;(3)14000人.
【解析】试题分析:(1)根据题意和统计图可以得到A组的人数;
(2)根据(1)中补全的统计图可以得到这组数据的中位数落在哪一组;
(3)根据统计图中的数据可以估计该地区达到国家规定的每天在校体育锻炼时间的人数.
试题解析:(1)由统计图可得,
A组人数为:60÷24%﹣60﹣120﹣20=50,
补全的条形统计图如右图所示,
(2)由补全的条形统计图可得,中位数落在C组,
(3)由题意可得,该地区25000名中学生中,达到国家规定的每天在校体育锻炼时间的人数约有:25000×(48%+8%)=14000(人),
【点睛】本题考查中位数、用样本估计总体、扇形统计图、条形统计图,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.
(1)4双;(2)6双;(3)2900元.
【解析】试题分析:(1)由统计图可知第4天A款运动鞋销量是6双且B款运动鞋的销售量是A款的可得;
(2)根据平均数与中位数定义求解可得;
(3)设A款运动鞋的销售单价为x元/双,B款运动鞋的销售单价为x元/双,根据第1天和第5天的总销售额列方程组求出A.B款运动鞋单价,即可得解.
试题解析:(1)解:6×(双 )
∴第4天B款运动鞋的销售量是4双;
(2)解:B款运动鞋每天销售量的平均数为(双 ),
中位数为6 (双 )
(3)解:设A款运动鞋的销售单价为x元/双,B款运动鞋的销售单价为y元/双.
由题意得: ,解得 ,
∴第3天的总销售额为(元)
【分析】(1)根据表格确定出m与n的值即可;
(2)补全条形统计图即可;
(3)确定出20名“健步走运动”团队成员一天行走的步数的中位数的范围即可;
(4)根据样本中的步数少于8500步的百分比,乘以200即可得到结果.
解:(1)根据表格得:5500≤x<6500的有:5640与6430,即m=2,
8500≤x<9500的有:8648,8753,9450,即n=3;
故答案为:2;3;
(2)补全条形统计图,如图所示:
(3)这20名“健步走运动”团队成员一天行走的步数的中位数落在B组;
故答案为:B;
(4)根据题意得:200×=160(人),
则估计一天行走的步数少于8500步的人数约为160人.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
6.1.2 中位数同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.把一组数据按从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,那么位于中间的数称为这组数据的中位数;如果数据的个数是偶数,那么位于中间的两个数的平均数称为这组数据的中位数.
2.中位数把一组数据分成相同数目的两部分,其中一部分都小于或等于中位数,而另一部分都大于或等于中位数,因此,中位数常用来描述“中间位置”或“中等水平”,但中位数没有利用数据组中所有的信息.
基础知识和能力拓展精练
1 、选择题
一组数据1,8,4,2,2,5的中位数是( )
A. 2 B. 3 C. 4 D. 5
假设五个相异正整数的平均数是15,中位数是18,则这五个相异正整数中的最大数的最大值为( )
A. 24 B. 32 C. 35 D. 40
根据下表中的信息解决问题:
若该组数据的中位数不大于38,则符合条件的正数的取值共有( )
A. 3个 B. 4个 C. 5个 D. 6个
已知八年级(4)班全班35人身高的平均数与中位数都是150cm,但后来发现其中有一位同学的身高登记错误,误将160cm写成166cm,正确的平均数为a cm,中位数为b cm,关于平均数a的叙述,下列正确的是( )
A.大于158 B.小于158 C.等于158 D.无法确定
贵阳市“阳光小区”开展“节约用水,从我做起”的活动,一个月后,社区居委会从小区住户中抽取10个家庭与他们上个月的用水量进行比较,统计出节水情况如表:
节水量(m3) 0.3 0.4 0.5 0.6 0.7
家庭数(个) 2 2 4 1 1
那么这10个家庭的节水量(m3)的平均数和中位数分别是( )
A.0.47和0.5 B.0.5和0.5 C.0.47和4 D.0.5和4
如表为初三(1)班全部43名同学某次数学测验成绩的统计结果,则下列说法正确的是( )
成绩(分) 70 80 90
男生(人) 5 10 7
女生(人) 4 13 4
A.男生的平均成绩大于女生的平均成绩
B.男生的平均成绩小于女生的平均成绩
C.男生成绩的中位数大于女生成绩的中位数
D.男生成绩的中位数小于女生成绩的中位数
某班组织了一次读书活动,统计了10名同学在一周内的读书时间,他们一周内的读书时间累计如表,则这10名同学一周内累计读书时间的中位数是( )
一周内累计的读书时间(小时) 5 8 10 14
人数(个) 1 4 3 2
A.8 B. 7 C. 9 D. 10
某班50名学生期末考试数学成绩(单位:分)的频率分布直方图如图所示,其中
数据不在分点上,对图中提供的信息作出如下的判断:
(1)成绩在49.5分~59.5分段的人数与89.5分~100分段的人数相等;
(2)成绩在79.5~89.5分段的人数占30%;
(3)成绩在79.5分以上的学生有20人;
(4)本次考试成绩的中位数落在69.5~79.5分段内.
其中正确的判断有( )
A.4个 B.3个 C.2个 D.1个
如图是根据我市某天七个整点时的气温绘制成的统计图,则这七个整点时气温的中位数和平均数分别是( )
A.30,28 B.26,26 C.31,30 D.26,22
2 、填空题
某校九年级(1)班40名同学中,14岁的有1人,15岁的有21人,16岁的有16人,17岁的有2人,则这个班同学年龄的中位数是 岁.
一组数据2,3,x,5,7的平均数是5,则这组数据的中位数是 .
聚奎中学“元旦艺术节”的校园十佳歌手比赛决赛中,参加比赛的 10 名选手成绩统计如图所示,则这 10 名学生成绩的中位数是_____.
某射击俱乐部将11名成员在某次射击训练中取得的成绩绘制成如图所示的条形统计图.由图可知,11名成员射击成绩的中位数是 环.
某班体育委员对本班学生一周锻炼时间(单位:小时)进行了统计,绘制了如图所示的折线统计图,则该班这些学生一周锻炼时间的中位数是 小时.
3 、解答题
为了解中学生的体能情况,某校抽取了50名八年级学生进行一分钟跳绳次数测试,将所得数据整理后,画出了频数分布直方图如下图所示已知图中从左到右前第一、第二、第三、第五小组的频率分别为0.04 , 0.12 ,0.4 ,O.28 ,根据已知条件解答下列问题:
(1)第四个小组的频率是多少 你是怎样得到的
(2)这五小组的频数各是多少
(3)在这次跳绳中,跳绳次数的中位数落在第几小组内
(4)将频数分布直方图补全,并分别写出各个小组的频数,并画出频数分布折线图.
有100名学生参加两次科技知识测试,条形图显示两次测试的分数分布情况.
请你根据条形图提供的信息,回答下列问题(把答案填在题中横线上):
(1)两次测试最低分在第 次测试中;
(2)第 次测试成绩较好;
(3)第一次测试中,中位数在 分数段,第二次测试中,中位数在 分数段.
国家规定,“中小学生每天在校体育锻炼时间不小于1小时”,某地区就“每天在校体育锻炼时间”的问题随机调查了若干名中学生,根据调查结果制作如下统计图(不完整).其中分组情况:A组:时间小于0.5小时;B组:时间大于等于0.5小时且小于1小时;C组:时间大于等于1小时且小于1.5小时;D组:时间大于等于1.5小时.
根据以上信息,回答下列问题:
(1)A组的人数是 人,并补全条形统计图;
(2)本次调查数据的中位数落在组 ;
(3)根据统计数据估计该地区25000名中学生中,达到国家规定的每天在校体育锻炼时间的人数约有多少人.
某商场对A.B两款运动鞋的销售情况进行了为期5天的统计,得到了这两款运动鞋每天的销售量及总销售额统计图(如图所示).已知第4天B款运动鞋的销售量是A款的.
(1)求第4天B款运动鞋的销售量.
(2)这5天期间,B款运动鞋每天销售量的平均数和中位数分别是多少?
(3)若在这5天期间两款运动鞋的销售单价保持不变,求第3天的总销售额(销售额=销售单价×销售量).
在一次社会调查活动中,小李收集到某“健步走运动”团队20名成员一天行走的步数,记录如下:
5640 6430 6520 6798 7325
8430 8215 7453 7446 6754
7638 6834 7326 6830 8648
8753 9450 9865 7290 7850
对这20个数据按组距1000进行分组,并统计整理,绘制了如下不完整的统计图表,步数分布统计图.
组别 步数分组 频数
A 5500≤x<6500 m
B 6500≤x<7500 10
C 7500≤x<8500 4
D 8500≤x<9500 n
E 9500≤x<10500 1
根据以上信息解答下列问题:
(1)填空:m= ,n= ;
(2)请补全条形统计图;
(3)这20名“健步走运动”团队成员一天行走的步数的中位数落在 组;
(4)若该团队共有200人,请估计其中一天行走步数少于8500步的人数.
答案解析
1 、选择题
B
【解析】将数据重新排列得:1、2、2、4、5、8,
则其中位数为 =3,
故选:B.
C
【解析】要使最大值最大,就要使其他的4个数尽量小,
设最大值为x,
∵五个相异正整数的平均数是15,中位数是18,
∴五个相异正整数的和是75,有两个比18小,两个比18大,
∴满足条件的五个数为:1, 2 ,18, 19, x,
∴x=75-19-1-2-18=35,
故选C.
C
【解析】解:当a=1时,有19个数据,最中间是:第10个数据,则中位数是38;
当a=2时,有20个数据,最中间是:第10和11个数据,则中位数是38;
当a=3时,有21个数据,最中间是:第11个数据,则中位数是38;
当a=4时,有22个数据,最中间是:第11和12个数据,则中位数是38;
当a=5时,有23个数据,最中间是:第12个数据,则中位数是38;
当a=6时,有24个数据,最中间是:第12和13个数据,则中位数是38.5;
故该组数据的中位数不大于38,则符合条件的正整数a的取值共有:5个.
故选C.
B
【解析】已知在错误登记中全班35人身高的平均数是150cm,则总身高总和为35×150=5250;修改后,减少了6厘米,为5244厘米,则正确的平均数为a=厘米,小于158cm.故选B.
【分析】找中位数要把数据按从小到大的顺序排列,位于最中间的一个数或两个数的平均数为中位数;平均数是指在一组数据中所有数据之和再除以数据的个数.
解:这10个数据的平均数为=0.47,
中位数为=0.5,
故选:A
【分析】根据平均数的定义分别求出男生与女生的平均成绩,再根据中位数的定义分别求出男生与女生成绩的中位数即可求解.
解:∵男生的平均成绩是:(70×5+80×10+90×7)÷22=1780÷22=80,
女生的平均成绩是:(70×4+80×13+90×4)÷21=1680÷21=80,
∴男生的平均成绩大于女生的平均成绩.
∵男生一共22人,位于中间的两个数都是80,所以中位数是(80+80)÷2=80,
女生一共21人,位于最中间的一个数是80,所以中位数是80,
∴男生成绩的中位数等于女生成绩的中位数.
故选A.
分析:根据中位数的概念求解.
解答: 解:∵共有10名同学,
∴第5名和第6名同学的读书时间的平均数为中位数,
则中位数为:=9.
故选C.
点评:本题考查了中位数的知识,将一组数据按照从小到大(或从大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果这组数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数.
分析:根据频数分布直方图的特点,以及中位数的定义进行解答.
解:(1)从频率分布直方图上看成绩在49.5分~59.5分段的人数与89.5分~100分段的人数相等,故选项正确;
(2)从频率分布直方图上看出:成绩在79.5~89.5分段的人数30%,故选项正确;
(3)成绩在79.5分以上的学生有50×(30%+10%)=20人,故选项正确;
(4)将该组数据按从小到大(或按从大到小)的顺序排列,本次考试成绩的中位数落在69.5~79.5分段内,故选项正确.
故选A.
【分析】此题根据中位数,平均数的定义解答.
解:由图可知,把7个数据从小到大排列为22,22,23,26,28,30,31,中位数是第4位数,第4位是26,所以中位数是26.
平均数是(22×2+23+26+28+30+31)÷7=26,所以平均数是26.
故选:B.
2 、填空题
分析: 根据中位数的定义找出第20和21个数的平均数,即可得出答案.
解答: 解:∵该班有40名同学,
∴这个班同学年龄的中位数是第20和21个数的平均数,
∵15岁的有21人,
∴这个班同学年龄的中位数是15岁;
故答案为:15.
点评: 此题考查了中位数,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),熟练掌握中位数的定义是本题的关键.
【分析】求出x的值,然后将数据按照从小到大依次排列即可求出中位数.
解:x=5×5﹣2﹣3﹣5﹣7=8,
这组数据为2,3,5,7,8,
故中位数为5.
8.5
【解析】分析:根据中位数的定义找出最中间的两个数,再求出它们的平均数即可.
详解:∵共有10名学生,
∴这10名学生成绩的中位数是第5和6个数的平均数,
∵第5和6个数分别是:8.5,8.5,
∴10名学生成绩的中位数是(8.5+8.5)÷2=8.5;
故答案为:8.5.
点睛:此题考查了中位数,中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.
【分析】11名成员射击成绩处在第6位的是8,则中位数为8.
解:∵按大小排列在中间的射击成绩为8环,则中位数为8.
故答案为:8.
【分析】根据统计图中的数据可以得到一共多少人,然后根据中位数的定义即可求得这组数据的中位数.
解:由统计图可知,
一共有:6+9+10+8+7=40(人),
∴该班这些学生一周锻炼时间的中位数是第20个和21个学生对应的数据的平均数,
∴该班这些学生一周锻炼时间的中位数是11,
故答案为:11.
3 、解答题
答案见解析
【解析】试题分析:(1)用1减去其余四组的频率即可;
(2)利用频数=频率乘总数得到;
(3)中位数是第25个同学、第26个同学跳绳次数之和的一半;
(4)依数画图即可.
试题解析:解:(1)由1减去已知4个小组的频率之和得到结果,第四个小组的频率=1﹣(0.04+0.12+0.4+0.28)=0.16;
(2)由频率=,且知各小组的频率分别为0.04,0.12,0.4,0.16,0.28及总人数为50,故有50×0.04=2,50×0.12=6,50×0.4=20,50×0.16=8,50×0.28=14,从而可知前5个小组的频数分别为2,6,20,8,14;
(3)由中位数应是第25个同学、第26个同学跳绳次数之和的一半.
由频数分布直方图可知,第25个同学、第26个同学跳绳次数均落在第三个小组内.
故而可知在这次测试中,跳绳次数的中位数落在第三小组内;
(4)由于第四小组的频数为8,第一小组频数为2,故第四小组的小长方形的高应是第一小组小长方形的高的4倍.
点睛:本题考查了读频数分布直方图的能力和利用统计图获取信息的能力.也考查了频率和中位数的概念.
(1)一;(2)二;(3)20﹣39;40﹣59.
【解析】试题分析:(1)由统计图直接得到;
(2)看统计图判断;
(3)中位数是将数据从小到大排列,取中间两个数的平均数.
试题解析:解:(1)两次测试最低分在第一次测试中;
(2)第一次测试的低分较多,高分较少,所以第二次的测试成绩较好;
(3)取第50名与51名同学成绩的平均数,所以第一次测试中,中位数落在20﹣39分数段;第二次测试中,中位数落在40﹣59分数段.
(1)50,补图见解析;(2)C;(3)14000人.
【解析】试题分析:(1)根据题意和统计图可以得到A组的人数;
(2)根据(1)中补全的统计图可以得到这组数据的中位数落在哪一组;
(3)根据统计图中的数据可以估计该地区达到国家规定的每天在校体育锻炼时间的人数.
试题解析:(1)由统计图可得,
A组人数为:60÷24%﹣60﹣120﹣20=50,
补全的条形统计图如右图所示,
(2)由补全的条形统计图可得,中位数落在C组,
(3)由题意可得,该地区25000名中学生中,达到国家规定的每天在校体育锻炼时间的人数约有:25000×(48%+8%)=14000(人),
【点睛】本题考查中位数、用样本估计总体、扇形统计图、条形统计图,解题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答问题.
(1)4双;(2)6双;(3)2900元.
【解析】试题分析:(1)由统计图可知第4天A款运动鞋销量是6双且B款运动鞋的销售量是A款的可得;
(2)根据平均数与中位数定义求解可得;
(3)设A款运动鞋的销售单价为x元/双,B款运动鞋的销售单价为x元/双,根据第1天和第5天的总销售额列方程组求出A.B款运动鞋单价,即可得解.
试题解析:(1)解:6×(双 )
∴第4天B款运动鞋的销售量是4双;
(2)解:B款运动鞋每天销售量的平均数为(双 ),
中位数为6 (双 )
(3)解:设A款运动鞋的销售单价为x元/双,B款运动鞋的销售单价为y元/双.
由题意得: ,解得 ,
∴第3天的总销售额为(元)
【分析】(1)根据表格确定出m与n的值即可;
(2)补全条形统计图即可;
(3)确定出20名“健步走运动”团队成员一天行走的步数的中位数的范围即可;
(4)根据样本中的步数少于8500步的百分比,乘以200即可得到结果.
解:(1)根据表格得:5500≤x<6500的有:5640与6430,即m=2,
8500≤x<9500的有:8648,8753,9450,即n=3;
故答案为:2;3;
(2)补全条形统计图,如图所示:
(3)这20名“健步走运动”团队成员一天行走的步数的中位数落在B组;
故答案为:B;
(4)根据题意得:200×=160(人),
则估计一天行走的步数少于8500步的人数约为160人.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
