人教版初中数学八年级下册19.1变量与函数同步练习题(含答案)
文档属性
| 名称 | 人教版初中数学八年级下册19.1变量与函数同步练习题(含答案) | 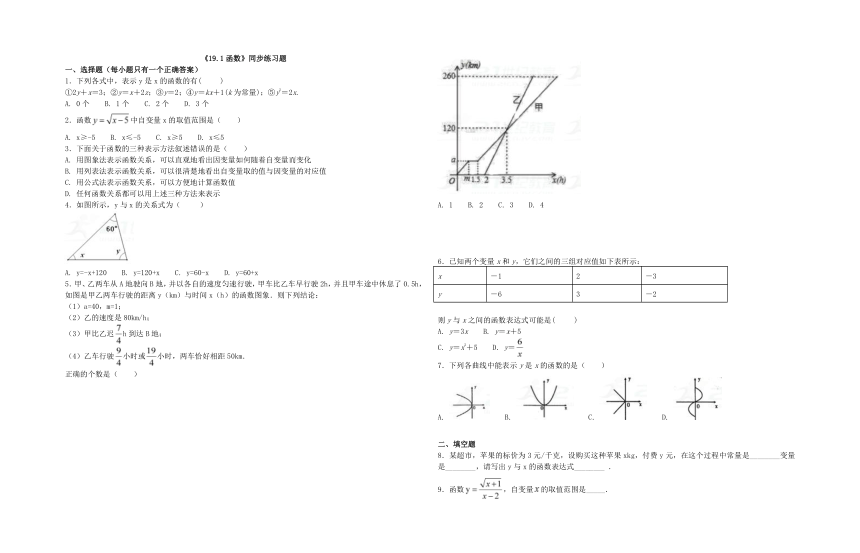 | |
| 格式 | zip | ||
| 文件大小 | 197.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-11 20:14:16 | ||
图片预览


文档简介
《19.1函数》同步练习题
一、选择题(每小题只有一个正确答案)
1.下列各式中,表示y是x的函数的有( )
①2y+x=3;②y=x+2z;③y=2;④y=kx+1(k为常量);⑤y2=2x.
A. 0个 B. 1个 C. 2个 D. 3个
2.函数中自变量x的取值范围是( )
A. x≥-5 B. x≤-5 C. x≥5 D. x≤5
3.下面关于函数的三种表示方法叙述错误的是( )
A. 用图象法表示函数关系,可以直观地看出因变量如何随着自变量而变化
B. 用列表法表示函数关系,可以很清楚地看出自变量取的值与因变量的对应值
C. 用公式法表示函数关系,可以方便地计算函数值
D. 任何函数关系都可以用上述三种方法来表示
4.如图所示,y与x的关系式为( )
A. y=-x+120 B. y=120+x C. y=60-x D. y=60+x
5.甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则下列结论:
(1)a=40,m=1;
(2)乙的速度是80km/h;
(3)甲比乙迟h到达B地;
(4)乙车行驶小时或小时,两车恰好相距50km.
正确的个数是( )
A. 1 B. 2 C. 3 D. 4
6.已知两个变量x和y,它们之间的三组对应值如下表所示:
x
-1
2
-3
y
-6
3
-2
则y与x之间的函数表达式可能是( )
A. y=3x B. y=x+5
C. y=x2+5 D. y=
7.下列各曲线中能表示y是x的函数的是( )
A. B. C. D.
二、填空题
8.某超市,苹果的标价为3元/千克,设购买这种苹果xkg,付费y元,在这个过程中常量是________变量是________,请写出y与x的函数表达式________ .
9.函数,自变量的取值范围是_____.
10.汽车的速度随时间变化的情况如图:
(1)这辆汽车的最高时速是_____;
(2)汽车在行驶了_____min后停了下来,停了_____min;
(3)汽车在第一次匀速行驶时共行驶了_____min,速度是_____,在这一段时间内,它走了_____km.
11.函数的三种表示方法是_________、_________、___________.
12.一空水池现需注满水,水池深 4.9m,现以不变的流量注水,数据如下表所示:
注水时间 t(h)
0.5
1
1.5
2
水的深度 h(m)
0.7
1.4
2.1
2.8
(1)上表反映的变量关系中,注水时间 t 是_____,水的深度 h 是_____.
(2)注满水池需要的时间是_____h.
三、解答题
13.求下列函数中自变量的取值范围.
;
;
;
;
.
14.写出下列问题中的关系式,并指出其中的变量和常量.
(1)直角三角形中一个锐角a与另一个锐角β之间的关系;
(2)一盛满30吨水的水箱,每小时流出0.5吨水,试用流水时间t(小时)表示水箱中的剩水量y(吨).
15.为了解某种车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来, 制成如表:
汽车行驶时间 t(小时)
0
1
2
3
…
油箱剩余油量 Q(升)
100
94
88
82
…
(1)上表反映的两个变量中,自变量是 ,因变量是 ;
(2)根据上表可知,该车油箱的大小为 升,每小时耗油 升;
(3)请求出两个变量之间的关系式(用 t 来表示 Q).
参考答案
1.B
【解析】①中表示y是x的,其它都不是。 ②还有变量z,③没有变量x, ④时,就不是了。 ⑤时,,有两个数值与之对应,y不是x的函数。股选B.
2.C
【解析】分析: 根据被开方数大于等于0列式计算即可得解.
详解: 由题意得,x?5?0,
解得x?5.
故选:C.
点睛: 本题考查了函数自变量的范围,一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.
3.D
【解析】分析:根据函数的表示方法的优缺点分析解答即可.
详解:A.用图象法表示函数关系,可以直观地看出因变量如何随着自变量而变化,正确;
B.用列表法表示函数关系,可以很清楚地看出自变量取的值与因变量的对应值,正确;
C.用公式法表示函数关系,可以方便地计算函数值,正确;
D.并不是任何函数关系都可以用上述三种方法来表示,错误.
故选D.
点睛:本题考查了函数的表示方法问题,关键是根据函数的表示方法的优缺点分析解答.
4.A
【解析】分析:根据三角形内角和为180°得出关系式.
详解:根据三角形内角和定理可知:x+y+60=180,则y=-x+120,故选A.
点睛:本题主要考查的就是三角形的内角和定理,属于基础题型.解答这个问题的关键就是明确三角形内角和定理.
5.C
【解析】(1)由题意,得m=1.5﹣0.5=1.
120÷(3.5﹣0.5)=40(km/h),则a=40,故(1)正确;
(2)120÷(3.5﹣2)=80km/h(千米/小时),故(2)正确;
(3)设甲车休息之后行驶路程y(km)与时间x(h)的函数关系式为y=kx+b,由题意,得
解得:
∴y=40x﹣20,
根据图形得知:甲、乙两车中先到达B地的是乙车,
把y=260代入y=40x﹣20得,x=7,
∵乙车的行驶速度:80km/h,
∴乙车的行驶260km需要260÷80=3.25h,
∴7﹣(2+3.25)=h,
∴甲比乙迟h到达B地,故(3)正确;
(4)当1.5<x≤7时,y=40x﹣20.
设乙车行驶的路程y与时间x之间的解析式为y=k'x+b',由题意得
解得:
∴y=80x﹣160.
当40x﹣20﹣50=80x﹣160时,
解得:x=.
当40x﹣20+50=80x﹣160时,
解得:x=.
∴﹣2=, ﹣2=.
所以乙车行驶小时或小时,两车恰好相距50km,故(4)错误.
故选C.
6.D
【解析】试题解析:A. 将表格对应数据代入,不符合方程 故错误;
B. 将表格对应数据代入,不符合方程 故错误.
C. 将表格对应数据代入,不符合方程 故错误;
D. 将表格对应数据代入,符合方程,正确.
故选D.
7.B
【解析】因为对于函数中自变量x的取值,y有唯一一个值与之对应,故选B.
8. 3 x、y y=3x
【解析】分析:根据常量与变量定义即可得知,题中的关系式为:总花费=单价×数量,把相关数值代入即可得函数表达式.
详解:
∵在购买苹果的过程中,苹果的单价3元/千克不变,所付费用y随购买数量xkg的变化而变化, ∴这个过程中,常量是3,变量是x、y,且y=3x, 故答案为:3,x、y,y=3x.
点睛:考查了函数的定义和列函数关系式.函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量.
9..
【解析】试题分析:根据题意可知:二次根式的被开方数为非负数,分式的分母不为零,则x+1≥0且x-2≠0,解得:x≥-1且x≠2.
10. 120 10 1 4 90 6
【解析】(1)这辆汽车的最高时速是120km/h;
(2)汽车在行驶了10min后停了下来,停了1min;
(3)汽车在第一次匀速行驶时共行驶了4min,速度是90km/h,在这一段时间内,它走了6km.
故答案为:(1)120;(2)10,1;(3)4,90,6
11. 图象法 列表法 解析式法
【解析】函数有三种表示方法——图象法、列表法、解析式法,
故答案为:图象法、列表法、解析式法.
【点睛】本题考查了函数的表达方式,是概念性问题,熟知课本中的概念是解题的关键.
12. 自变量 因变量 3.5
【解析】(1)由题意可知,上表反映的变量关系中,注水时间t是:自变量;水的深度h是:因变量;
(2)观察、分析表中数据可知,每0.5小时,水的深度增加0.7m,
∴注满水池需要的时间为:4.9÷0.7×0.5=3.5(小时).
故答案为:(1)自变量;(2)因变量;(3)3.5.
13.(1)全体实数;(2);(3);(4);(5)
【解析】分析:根据当函数表达式是整式时,自变量可取全体实数,当函数表达式是分式时,考虑分式的分母不能为0,当函数表达式是二次根式时,被开方数非负进行解答.
本题解析: 的取值范围为全体实数;
解不等式,得,故x的取值范围为;
解不等式,得,故x的取值范围为;
解不等式,得,故x的取值范围为;
解不等式组得,故x的取值范围为.
点睛:本题考查的是函数自变量的取值范围的确定,函数自变量的范围一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数为非负数.
14.(1)α=90°﹣β;常量是90,变量是α,β;(2)y=30﹣0.5t.常量是30,0.5,变量是y、t
【解析】试题分析:(1)根据直角三角形的性质:直角三角形中,两锐角互余可得根据变量和常量的定义:在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量可得答案. (2)根据题意可得剩余水量=原有水量-流出水量可的函数关系式.
试题解析:(1)由题意得: ,即;常量是90,变量是.
(2)依题意得:y=30﹣0.5t.常量是30,0.5,变量是y、t.
15.(1)t,Q;(2)100,6;(3)
【解析】试题分析:(1)根据变量的定义即可判断.
(2)当t=0时,此时油箱剩余油量即为油箱大小,根据表格可知,1小时共耗油6升.
(3)根据(2)即可求出Q的关系式.
试题解析:解:(1)t;Q.
(2)100;6.
(3)由(2)可知:Q=100﹣6t.
一、选择题(每小题只有一个正确答案)
1.下列各式中,表示y是x的函数的有( )
①2y+x=3;②y=x+2z;③y=2;④y=kx+1(k为常量);⑤y2=2x.
A. 0个 B. 1个 C. 2个 D. 3个
2.函数中自变量x的取值范围是( )
A. x≥-5 B. x≤-5 C. x≥5 D. x≤5
3.下面关于函数的三种表示方法叙述错误的是( )
A. 用图象法表示函数关系,可以直观地看出因变量如何随着自变量而变化
B. 用列表法表示函数关系,可以很清楚地看出自变量取的值与因变量的对应值
C. 用公式法表示函数关系,可以方便地计算函数值
D. 任何函数关系都可以用上述三种方法来表示
4.如图所示,y与x的关系式为( )
A. y=-x+120 B. y=120+x C. y=60-x D. y=60+x
5.甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2h,并且甲车途中休息了0.5h,如图是甲乙两车行驶的距离y(km)与时间x(h)的函数图象.则下列结论:
(1)a=40,m=1;
(2)乙的速度是80km/h;
(3)甲比乙迟h到达B地;
(4)乙车行驶小时或小时,两车恰好相距50km.
正确的个数是( )
A. 1 B. 2 C. 3 D. 4
6.已知两个变量x和y,它们之间的三组对应值如下表所示:
x
-1
2
-3
y
-6
3
-2
则y与x之间的函数表达式可能是( )
A. y=3x B. y=x+5
C. y=x2+5 D. y=
7.下列各曲线中能表示y是x的函数的是( )
A. B. C. D.
二、填空题
8.某超市,苹果的标价为3元/千克,设购买这种苹果xkg,付费y元,在这个过程中常量是________变量是________,请写出y与x的函数表达式________ .
9.函数,自变量的取值范围是_____.
10.汽车的速度随时间变化的情况如图:
(1)这辆汽车的最高时速是_____;
(2)汽车在行驶了_____min后停了下来,停了_____min;
(3)汽车在第一次匀速行驶时共行驶了_____min,速度是_____,在这一段时间内,它走了_____km.
11.函数的三种表示方法是_________、_________、___________.
12.一空水池现需注满水,水池深 4.9m,现以不变的流量注水,数据如下表所示:
注水时间 t(h)
0.5
1
1.5
2
水的深度 h(m)
0.7
1.4
2.1
2.8
(1)上表反映的变量关系中,注水时间 t 是_____,水的深度 h 是_____.
(2)注满水池需要的时间是_____h.
三、解答题
13.求下列函数中自变量的取值范围.
;
;
;
;
.
14.写出下列问题中的关系式,并指出其中的变量和常量.
(1)直角三角形中一个锐角a与另一个锐角β之间的关系;
(2)一盛满30吨水的水箱,每小时流出0.5吨水,试用流水时间t(小时)表示水箱中的剩水量y(吨).
15.为了解某种车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来, 制成如表:
汽车行驶时间 t(小时)
0
1
2
3
…
油箱剩余油量 Q(升)
100
94
88
82
…
(1)上表反映的两个变量中,自变量是 ,因变量是 ;
(2)根据上表可知,该车油箱的大小为 升,每小时耗油 升;
(3)请求出两个变量之间的关系式(用 t 来表示 Q).
参考答案
1.B
【解析】①中表示y是x的,其它都不是。 ②还有变量z,③没有变量x, ④时,就不是了。 ⑤时,,有两个数值与之对应,y不是x的函数。股选B.
2.C
【解析】分析: 根据被开方数大于等于0列式计算即可得解.
详解: 由题意得,x?5?0,
解得x?5.
故选:C.
点睛: 本题考查了函数自变量的范围,一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.
3.D
【解析】分析:根据函数的表示方法的优缺点分析解答即可.
详解:A.用图象法表示函数关系,可以直观地看出因变量如何随着自变量而变化,正确;
B.用列表法表示函数关系,可以很清楚地看出自变量取的值与因变量的对应值,正确;
C.用公式法表示函数关系,可以方便地计算函数值,正确;
D.并不是任何函数关系都可以用上述三种方法来表示,错误.
故选D.
点睛:本题考查了函数的表示方法问题,关键是根据函数的表示方法的优缺点分析解答.
4.A
【解析】分析:根据三角形内角和为180°得出关系式.
详解:根据三角形内角和定理可知:x+y+60=180,则y=-x+120,故选A.
点睛:本题主要考查的就是三角形的内角和定理,属于基础题型.解答这个问题的关键就是明确三角形内角和定理.
5.C
【解析】(1)由题意,得m=1.5﹣0.5=1.
120÷(3.5﹣0.5)=40(km/h),则a=40,故(1)正确;
(2)120÷(3.5﹣2)=80km/h(千米/小时),故(2)正确;
(3)设甲车休息之后行驶路程y(km)与时间x(h)的函数关系式为y=kx+b,由题意,得
解得:
∴y=40x﹣20,
根据图形得知:甲、乙两车中先到达B地的是乙车,
把y=260代入y=40x﹣20得,x=7,
∵乙车的行驶速度:80km/h,
∴乙车的行驶260km需要260÷80=3.25h,
∴7﹣(2+3.25)=h,
∴甲比乙迟h到达B地,故(3)正确;
(4)当1.5<x≤7时,y=40x﹣20.
设乙车行驶的路程y与时间x之间的解析式为y=k'x+b',由题意得
解得:
∴y=80x﹣160.
当40x﹣20﹣50=80x﹣160时,
解得:x=.
当40x﹣20+50=80x﹣160时,
解得:x=.
∴﹣2=, ﹣2=.
所以乙车行驶小时或小时,两车恰好相距50km,故(4)错误.
故选C.
6.D
【解析】试题解析:A. 将表格对应数据代入,不符合方程 故错误;
B. 将表格对应数据代入,不符合方程 故错误.
C. 将表格对应数据代入,不符合方程 故错误;
D. 将表格对应数据代入,符合方程,正确.
故选D.
7.B
【解析】因为对于函数中自变量x的取值,y有唯一一个值与之对应,故选B.
8. 3 x、y y=3x
【解析】分析:根据常量与变量定义即可得知,题中的关系式为:总花费=单价×数量,把相关数值代入即可得函数表达式.
详解:
∵在购买苹果的过程中,苹果的单价3元/千克不变,所付费用y随购买数量xkg的变化而变化, ∴这个过程中,常量是3,变量是x、y,且y=3x, 故答案为:3,x、y,y=3x.
点睛:考查了函数的定义和列函数关系式.函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量.
9..
【解析】试题分析:根据题意可知:二次根式的被开方数为非负数,分式的分母不为零,则x+1≥0且x-2≠0,解得:x≥-1且x≠2.
10. 120 10 1 4 90 6
【解析】(1)这辆汽车的最高时速是120km/h;
(2)汽车在行驶了10min后停了下来,停了1min;
(3)汽车在第一次匀速行驶时共行驶了4min,速度是90km/h,在这一段时间内,它走了6km.
故答案为:(1)120;(2)10,1;(3)4,90,6
11. 图象法 列表法 解析式法
【解析】函数有三种表示方法——图象法、列表法、解析式法,
故答案为:图象法、列表法、解析式法.
【点睛】本题考查了函数的表达方式,是概念性问题,熟知课本中的概念是解题的关键.
12. 自变量 因变量 3.5
【解析】(1)由题意可知,上表反映的变量关系中,注水时间t是:自变量;水的深度h是:因变量;
(2)观察、分析表中数据可知,每0.5小时,水的深度增加0.7m,
∴注满水池需要的时间为:4.9÷0.7×0.5=3.5(小时).
故答案为:(1)自变量;(2)因变量;(3)3.5.
13.(1)全体实数;(2);(3);(4);(5)
【解析】分析:根据当函数表达式是整式时,自变量可取全体实数,当函数表达式是分式时,考虑分式的分母不能为0,当函数表达式是二次根式时,被开方数非负进行解答.
本题解析: 的取值范围为全体实数;
解不等式,得,故x的取值范围为;
解不等式,得,故x的取值范围为;
解不等式,得,故x的取值范围为;
解不等式组得,故x的取值范围为.
点睛:本题考查的是函数自变量的取值范围的确定,函数自变量的范围一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数为非负数.
14.(1)α=90°﹣β;常量是90,变量是α,β;(2)y=30﹣0.5t.常量是30,0.5,变量是y、t
【解析】试题分析:(1)根据直角三角形的性质:直角三角形中,两锐角互余可得根据变量和常量的定义:在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量可得答案. (2)根据题意可得剩余水量=原有水量-流出水量可的函数关系式.
试题解析:(1)由题意得: ,即;常量是90,变量是.
(2)依题意得:y=30﹣0.5t.常量是30,0.5,变量是y、t.
15.(1)t,Q;(2)100,6;(3)
【解析】试题分析:(1)根据变量的定义即可判断.
(2)当t=0时,此时油箱剩余油量即为油箱大小,根据表格可知,1小时共耗油6升.
(3)根据(2)即可求出Q的关系式.
试题解析:解:(1)t;Q.
(2)100;6.
(3)由(2)可知:Q=100﹣6t.
