数学六年级下人教版第4单元 正比例 和反比例“练习九”(含解析)
文档属性
| 名称 | 数学六年级下人教版第4单元 正比例 和反比例“练习九”(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 995.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-12 05:45:08 | ||
图片预览


文档简介
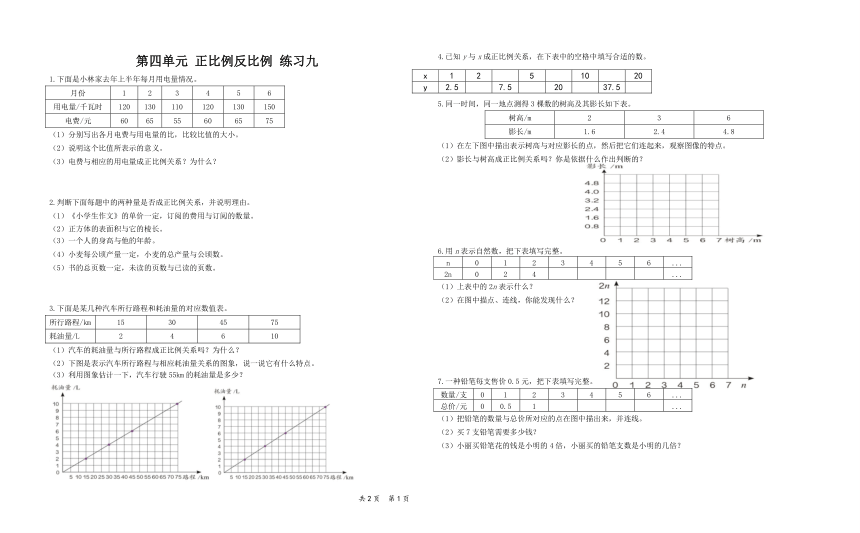
第四单元 正比例反比例 练习九
1.下面是小林家去年上半年每月用电量情况。
月份
1
2
3
4
5
6
用电量/千瓦时
120
130
110
120
130
150
电费/元
60
65
55
60
65
75
(1)分别写出各月电费与用电量的比,比较比值的大小。
(2)说明这个比值所表示的意义。
(3)电费与相应的用电量成正比例关系?为什么?
2.判断下面每题中的两种量是否成正比例关系,并说明理由。
(1)《小学生作文》的单价一定,订阅的费用与订阅的数量。
(2)正方体的表面积与它的棱长。
(3)一个人的身高与他的年龄。 (4)小麦每公顷产量一定,小麦的总产量与公顷数。
(5)书的总页数一定,未读的页数与已读的页数。
3.下面是某几种汽车所行路程和耗油量的对应数值表。
所行路程/km
15
30
45
75
耗油量/L
2
4
6
10
(1)汽车的耗油量与所行路程成正比例关系吗?为什么?
(2)下图是表示汽车所行路程与相应耗油量关系的图象,说一说它有什么特点。
(3)利用图象估计一下,汽车行驶55km的耗油量是多少?
4.已知y与x成正比例关系,在下表中的空格中填写合适的数。
x
1
2
5
10
20
y
2.5
7.5
20
37.5
5.同一时间,同一地点测得3棵数的树高及其影长如下表。
树高/m
2
3
6
影长/m
1.6
2.4
4.8
(1)在左下图中描出表示树高与对应影长的点,然后把它们连起来,观察图像的特点。
(2)影长与树高成正比例关系吗?你是依据什么作出判断的?
6.用n表示自然数,把下表填写完整。
n
0
1
2
3
4
5
6
...
2n
0
2
4
...
(1)上表中的2n表示什么?
(2)在图中描点、连线,你能发现什么?
7.一种铅笔每支售价0.5元,把下表填写完整。
数量/支
0
1
2
3
4
5
6
...
总价/元
0
0.5
1
...
(1)把铅笔的数量与总价所对应的点在图中描出来,并连线。
(2)买7支铅笔需要多少钱?
(3)小丽买铅笔花的钱是小明的4倍,小丽买的铅笔支数是小明的几倍?
8.给一间长9m、宽6m的教室铺地砖,每块地砖的面积与所需地砖数量如下表。
每块地砖的面积/cm
900
1800
3600
所需地砖数量/块
600
300
150
所需地砖数量与每块地砖的面积是否成反比例关系?为什么?
9.食品加工厂准备把一批新酿的醋装瓶运往商店。
每瓶容量/mL
250
500
750
1500
所装瓶数/瓶
1200
600
400
200
所装瓶数与每瓶容量是否成反比例关系?为什么?
10.下表中x和y两个量成反比例关系,请把表格填写完整。
x
2
40
y
5
0.1
11.判断下面各题中的两种量是否成反比例关系,并说明理由。
(1)煤的数量一定,使用天数与每天的平均用煤量。
(2)全班的人数一定,按各组人数相等的要求分组,组数与每组的人数。
(3)圆柱体积一定,圆柱的底面积与高。
(4)在一块菜地上种的黄瓜与西红柿的面积。
(5)书的总册数一定,按各包册数相等的规定包壮书,包数与每包的册数。
12.一个手机组装车间要完成一批任务,每天组装手机的数量与需要的天数如下表。
每天组装的数量/部
500
600
800
1000
1200
时间/天
24
20
15
12
10
(1)每天组装的数量用p表示,需要的天数用t表示。你能用式子表示出p、t和组装的手机总数之间的关系吗?
(2)p与t成什么比例关系?
(3)如果这批组装任务需要8天完成。每天组装多少部手机?
13.京沪高铁的火车平均行驶速度与行驶完全程所需时间如下表。
速度/(km/h)
270
260
250
200
180
150
...
时间/h
5
5.2
6.5
...
(1)京沪高铁全长多少千米?
(2)如果用v表示火车的平均速度,t表示驶完全程所需时间。t与v成什么比例关系?你能写出这个关系式吗?
(3)如果火车的平均速度为325千米/时,驶完全程需要多长时间?
14.下面的图象表示斑马和长颈鹿的奔跑情况。
(1)斑马的奔跑路程与奔跑时间是否成正比例
关系?长颈鹿呢?
(2)估计一下,两种动物18分钟各跑多少千米?
(3)从图象上看,斑马跑的快还是长颈鹿跑的快?
15.*有x、y、z三个相关联的量,并有xy=z。
(1)当z一定时,x与y成______比例关系。
(2)当x一定时,z与y成______比例关系。
(3)当y一定时,z与x成______比例关系。
16.*一个长方形的面积是36cm2,用x和y表示它的长和宽。y与x成什么比例关系?如果把它们的关系用图象表示出来,图象是一条直线吗?
第四单元 正比例和反比例练习九(答案)
1.下面是小林家去年上半年每月用电量情况。
月份
1
2
3
4
5
6
用电量/千瓦时
120
130
110
120
130
150
电费/元
60
65
55
60
65
75
(1)分别写出各月电费与用电量的比,比较比值的大小。
(2)说明这个比值所表示的意义。
(3)电费与相应的用电量成正比例关系?为什么?
解:(1)60:120=65:130=55:110=60:120=65:130=75:150=0.5
(2)比值表示用电单价。
(3)成正比例关系,因为电费:用电量=单价(一定),比值一定。
2.判断下面每题中的两种量是否成正比例关系,并说明理由。
(1)《小学生作文》的单价一定,订阅的费用与订阅的数量。
(2)正方体的表面积与它的棱长。
(3)一个人的身高与他的年龄。 (4)小麦每公顷产量一定,小麦的总产量与公顷数。
(5)书的总页数一定,未读的页数与已读的页数。
解:(1)订阅的费用:订阅数量=单价(一定),所以订阅的费用与订阅的数量成正比例关系。
(2)正方体的表面积=棱长的平方×6,正方体的表面积与棱长的平方的比值一定,但与棱长的比值不一定,所以正方体的表面积与它的棱长不成比例关系。
(3)一个人的身高与他的年龄没有直接关系,所以一个人的身高与他的年龄不成比例关系。
(4)小麦的总产量:公顷数=每公顷产量,每公顷产量一定,所以小麦的总产量与公顷数成正比例关系。
(5)总页数=已读页数+未读页数,所以未读页数与已读的页数不成正比例关系。
3.下面是某几种汽车所行路程和耗油量的对应数值表。
所行路程/km
15
30
45
75
耗油量/L
2
4
6
10
(1)汽车的耗油量与所行路程成正比例关系吗?为什么?
(2)下图是表示汽车所行路程与相应耗油量关系的图象,说一说它有什么特点。
(3)利用图象估计一下,汽车行驶55km的耗油量是多少?
解:(1)成正比例关系,因为耗油量:所行路程=行驶1km的耗油量,而行驶1km的耗油量一定。
(2)图像是一条经过原点的直线。
(3)汽车行驶55km的耗油量大约是7.3L。
4.已知y与x成正比例关系,在下表中的空格中填写合适的数。
x
1
2
5
10
20
y
2.5
7.5
20
37.5
5.同一时间,同一地点测得3棵数的树高及其影长如下表。
树高/m
2
3
6
影长/m
1.6
2.4
4.8
(1)在左下图中描出表示树高与对应影长的点,然后把它们连起来,观察图像的特点。
(2)影长与树高成正比例关系吗?你是依据什么作出判断的?
解:(1)图像是一条经过原点的直线。
(2)成正比例关系,因为
6.用n表示自然数,把下表填写完整。
n
0
1
2
3
4
5
6
...
2n
0
2
4
6
8
10
12
...
(1)上表中的2n表示什么?
(2)在图中描点、连线,你能发现什么?
解:(1)2n表示自然数中的偶数。
(2)图像是一条经过原点的直线。
7.一种铅笔每支售价0.5元,把下表填写完整。
数量/支
0
1
2
3
4
5
6
...
总价/元
0
0.5
1
1.5
2
2.5
3
...
(1)把铅笔的数量与总价所对应的点在图中描出来,并连线。
(2)买7支铅笔需要多少钱?
(3)小丽买铅笔花的钱是小明的4倍,小丽买的铅笔支数
是小明的几倍?
解:(1)如右图:
(2)7×0.5=3.5(元)
答:买7支铅笔需要3.5元钱。
(3)小丽买的铅笔支数是小明的4倍。
8.给一间长9m、宽6m的教室铺地砖,每块地砖的面积与所需地砖数量如下表。
每块地砖的面积/cm
900
1800
3600
所需地砖数量/块
600
300
150
所需地砖数量与每块地砖的面积是否成反比例关系?为什么?
解:9×6=54(m) 900×600=540000(cm)=54(m)
1800×300=540000(cm)=54(m) 3600×150=540000(cm)=54(m)
答:所需地砖数量与每块地砖的面积成反比例,因为每块地砖的面积与所需地砖数量的乘积都等于教室的面积,教室的面积一定。
9.食品加工厂准备把一批新酿的醋装瓶运往商店。
每瓶容量/mL
250
500
750
1500
所装瓶数/瓶
1200
600
400
200
所装瓶数与每瓶容量是否成反比例关系?为什么?
解:250×1200=300000(mL)=300(L) 500×600=300000(mL)=300(L)
750×400=300000(mL)=300(L) 1500×200=300000(mL)=300(L)
答:所装瓶数与每瓶容量成反比例,因为每瓶容量与所装瓶数的乘积是这批醋的体积(一定)。
10.下表中x和y两个量成反比例关系,请把表格填写完整。
x
2
100
40
12
y
5
50
0.1
11.判断下面各题中的两种量是否成反比例关系,并说明理由。
(1)煤的数量一定,使用天数与每天的平均用煤量。
(2)全班的人数一定,按各组人数相等的要求分组,组数与每组的人数。
(3)圆柱体积一定,圆柱的底面积与高。
(4)在一块菜地上种的黄瓜与西红柿的面积。
(5)书的总册数一定,按各包册数相等的规定包壮书,包数与每包的册数。
解:(1)因为每天的平均用煤量×使用天数=煤的数量(一定),所以使用天数与每天的平均用煤量成反比例关系。
(2)因为每组人数×组数=全班的人数(一定),所以组数与每组的人数成反比例关系。
(3)因为圆柱的底面积×高=圆柱的体积(一定),所以圆柱的底面积与高成反比例关系。
(4)因为种黄瓜的面积与种西红柿的面积的和一定,而他们的乘积不一定,所以种黄瓜的面积与种西红柿的面积不成反比例关系。
(5)因为每包的册数×包数=书的总册数(一定),所以包数与每包的册数成反比例关系。
12.一个手机组装车间要完成一批任务,每天组装手机的数量与需要的天数如下表。
每天组装的数量/部
500
600
800
1000
1200
时间/天
24
20
15
12
10
(1)每天组装的数量用p表示,需要的天数用t表示。你能用式子表示出p、t和组装的手机总数之间的关系吗?
(2)p与t成什么比例关系?
(3)如果这批组装任务需要8天完成。每天组装多少部手机?
解:(1)pt=500×24=600×20=12000
(2)p与t成成反比例关系
(3)12000÷8=1500(部)
答:每天组装1500部手机。
13.京沪高铁的火车平均行驶速度与行驶完全程所需时间如下表。
速度/(km/h)
270
260
250
200
180
150
...
时间/h
5
5.2
6.5
...
(1)京沪高铁全长多少千米?
(2)如果用v表示火车的平均速度,t表示驶完全程所需时间。t与v成什么比例关系?你能写出这个关系式吗?
(3)如果火车的平均速度为325千米/时,驶完全程需要多长时间?
解:(1)260×5=1300(km)
答:京沪高铁全长1300千米。
(2)t与v成反比例关系; vt=1300
(3)1300÷325=4(小时)
答:驶完全程需要4小时。
14.下面的图象表示斑马和长颈鹿的奔跑情况。
(1)斑马的奔跑路程与奔跑时间是否成正比例关系?长颈鹿呢?
(2)估计一下,两种动物18分钟各跑多少千米?
(3)从图象上看,斑马跑的快还是长颈鹿跑的快?
解:(1)斑马的奔跑路程与奔跑时间成正比例关系,长颈鹿的奔跑路程与奔跑时间也成正比例关系。
(2)斑马和长颈鹿18分钟分别跑21.6千米14.4千米。
(3)斑马跑的快。
15.*有x、y、z三个相关联的量,并有xy=z。
(1)当z一定时,x与y成_ 反_比例关系。
(2)当x一定时,z与y成__正____比例关系。
(3)当y一定时,z与x成___正___比例关系。
16.*一个长方形的面积是36cm,用x和y表示它的长和宽。y与x成什么比例关系?如果把它们的关系用图象表示出来,图象是一条直线吗?
解:y与x成反比例关系,图象不是一条直线。
1.下面是小林家去年上半年每月用电量情况。
月份
1
2
3
4
5
6
用电量/千瓦时
120
130
110
120
130
150
电费/元
60
65
55
60
65
75
(1)分别写出各月电费与用电量的比,比较比值的大小。
(2)说明这个比值所表示的意义。
(3)电费与相应的用电量成正比例关系?为什么?
2.判断下面每题中的两种量是否成正比例关系,并说明理由。
(1)《小学生作文》的单价一定,订阅的费用与订阅的数量。
(2)正方体的表面积与它的棱长。
(3)一个人的身高与他的年龄。 (4)小麦每公顷产量一定,小麦的总产量与公顷数。
(5)书的总页数一定,未读的页数与已读的页数。
3.下面是某几种汽车所行路程和耗油量的对应数值表。
所行路程/km
15
30
45
75
耗油量/L
2
4
6
10
(1)汽车的耗油量与所行路程成正比例关系吗?为什么?
(2)下图是表示汽车所行路程与相应耗油量关系的图象,说一说它有什么特点。
(3)利用图象估计一下,汽车行驶55km的耗油量是多少?
4.已知y与x成正比例关系,在下表中的空格中填写合适的数。
x
1
2
5
10
20
y
2.5
7.5
20
37.5
5.同一时间,同一地点测得3棵数的树高及其影长如下表。
树高/m
2
3
6
影长/m
1.6
2.4
4.8
(1)在左下图中描出表示树高与对应影长的点,然后把它们连起来,观察图像的特点。
(2)影长与树高成正比例关系吗?你是依据什么作出判断的?
6.用n表示自然数,把下表填写完整。
n
0
1
2
3
4
5
6
...
2n
0
2
4
...
(1)上表中的2n表示什么?
(2)在图中描点、连线,你能发现什么?
7.一种铅笔每支售价0.5元,把下表填写完整。
数量/支
0
1
2
3
4
5
6
...
总价/元
0
0.5
1
...
(1)把铅笔的数量与总价所对应的点在图中描出来,并连线。
(2)买7支铅笔需要多少钱?
(3)小丽买铅笔花的钱是小明的4倍,小丽买的铅笔支数是小明的几倍?
8.给一间长9m、宽6m的教室铺地砖,每块地砖的面积与所需地砖数量如下表。
每块地砖的面积/cm
900
1800
3600
所需地砖数量/块
600
300
150
所需地砖数量与每块地砖的面积是否成反比例关系?为什么?
9.食品加工厂准备把一批新酿的醋装瓶运往商店。
每瓶容量/mL
250
500
750
1500
所装瓶数/瓶
1200
600
400
200
所装瓶数与每瓶容量是否成反比例关系?为什么?
10.下表中x和y两个量成反比例关系,请把表格填写完整。
x
2
40
y
5
0.1
11.判断下面各题中的两种量是否成反比例关系,并说明理由。
(1)煤的数量一定,使用天数与每天的平均用煤量。
(2)全班的人数一定,按各组人数相等的要求分组,组数与每组的人数。
(3)圆柱体积一定,圆柱的底面积与高。
(4)在一块菜地上种的黄瓜与西红柿的面积。
(5)书的总册数一定,按各包册数相等的规定包壮书,包数与每包的册数。
12.一个手机组装车间要完成一批任务,每天组装手机的数量与需要的天数如下表。
每天组装的数量/部
500
600
800
1000
1200
时间/天
24
20
15
12
10
(1)每天组装的数量用p表示,需要的天数用t表示。你能用式子表示出p、t和组装的手机总数之间的关系吗?
(2)p与t成什么比例关系?
(3)如果这批组装任务需要8天完成。每天组装多少部手机?
13.京沪高铁的火车平均行驶速度与行驶完全程所需时间如下表。
速度/(km/h)
270
260
250
200
180
150
...
时间/h
5
5.2
6.5
...
(1)京沪高铁全长多少千米?
(2)如果用v表示火车的平均速度,t表示驶完全程所需时间。t与v成什么比例关系?你能写出这个关系式吗?
(3)如果火车的平均速度为325千米/时,驶完全程需要多长时间?
14.下面的图象表示斑马和长颈鹿的奔跑情况。
(1)斑马的奔跑路程与奔跑时间是否成正比例
关系?长颈鹿呢?
(2)估计一下,两种动物18分钟各跑多少千米?
(3)从图象上看,斑马跑的快还是长颈鹿跑的快?
15.*有x、y、z三个相关联的量,并有xy=z。
(1)当z一定时,x与y成______比例关系。
(2)当x一定时,z与y成______比例关系。
(3)当y一定时,z与x成______比例关系。
16.*一个长方形的面积是36cm2,用x和y表示它的长和宽。y与x成什么比例关系?如果把它们的关系用图象表示出来,图象是一条直线吗?
第四单元 正比例和反比例练习九(答案)
1.下面是小林家去年上半年每月用电量情况。
月份
1
2
3
4
5
6
用电量/千瓦时
120
130
110
120
130
150
电费/元
60
65
55
60
65
75
(1)分别写出各月电费与用电量的比,比较比值的大小。
(2)说明这个比值所表示的意义。
(3)电费与相应的用电量成正比例关系?为什么?
解:(1)60:120=65:130=55:110=60:120=65:130=75:150=0.5
(2)比值表示用电单价。
(3)成正比例关系,因为电费:用电量=单价(一定),比值一定。
2.判断下面每题中的两种量是否成正比例关系,并说明理由。
(1)《小学生作文》的单价一定,订阅的费用与订阅的数量。
(2)正方体的表面积与它的棱长。
(3)一个人的身高与他的年龄。 (4)小麦每公顷产量一定,小麦的总产量与公顷数。
(5)书的总页数一定,未读的页数与已读的页数。
解:(1)订阅的费用:订阅数量=单价(一定),所以订阅的费用与订阅的数量成正比例关系。
(2)正方体的表面积=棱长的平方×6,正方体的表面积与棱长的平方的比值一定,但与棱长的比值不一定,所以正方体的表面积与它的棱长不成比例关系。
(3)一个人的身高与他的年龄没有直接关系,所以一个人的身高与他的年龄不成比例关系。
(4)小麦的总产量:公顷数=每公顷产量,每公顷产量一定,所以小麦的总产量与公顷数成正比例关系。
(5)总页数=已读页数+未读页数,所以未读页数与已读的页数不成正比例关系。
3.下面是某几种汽车所行路程和耗油量的对应数值表。
所行路程/km
15
30
45
75
耗油量/L
2
4
6
10
(1)汽车的耗油量与所行路程成正比例关系吗?为什么?
(2)下图是表示汽车所行路程与相应耗油量关系的图象,说一说它有什么特点。
(3)利用图象估计一下,汽车行驶55km的耗油量是多少?
解:(1)成正比例关系,因为耗油量:所行路程=行驶1km的耗油量,而行驶1km的耗油量一定。
(2)图像是一条经过原点的直线。
(3)汽车行驶55km的耗油量大约是7.3L。
4.已知y与x成正比例关系,在下表中的空格中填写合适的数。
x
1
2
5
10
20
y
2.5
7.5
20
37.5
5.同一时间,同一地点测得3棵数的树高及其影长如下表。
树高/m
2
3
6
影长/m
1.6
2.4
4.8
(1)在左下图中描出表示树高与对应影长的点,然后把它们连起来,观察图像的特点。
(2)影长与树高成正比例关系吗?你是依据什么作出判断的?
解:(1)图像是一条经过原点的直线。
(2)成正比例关系,因为
6.用n表示自然数,把下表填写完整。
n
0
1
2
3
4
5
6
...
2n
0
2
4
6
8
10
12
...
(1)上表中的2n表示什么?
(2)在图中描点、连线,你能发现什么?
解:(1)2n表示自然数中的偶数。
(2)图像是一条经过原点的直线。
7.一种铅笔每支售价0.5元,把下表填写完整。
数量/支
0
1
2
3
4
5
6
...
总价/元
0
0.5
1
1.5
2
2.5
3
...
(1)把铅笔的数量与总价所对应的点在图中描出来,并连线。
(2)买7支铅笔需要多少钱?
(3)小丽买铅笔花的钱是小明的4倍,小丽买的铅笔支数
是小明的几倍?
解:(1)如右图:
(2)7×0.5=3.5(元)
答:买7支铅笔需要3.5元钱。
(3)小丽买的铅笔支数是小明的4倍。
8.给一间长9m、宽6m的教室铺地砖,每块地砖的面积与所需地砖数量如下表。
每块地砖的面积/cm
900
1800
3600
所需地砖数量/块
600
300
150
所需地砖数量与每块地砖的面积是否成反比例关系?为什么?
解:9×6=54(m) 900×600=540000(cm)=54(m)
1800×300=540000(cm)=54(m) 3600×150=540000(cm)=54(m)
答:所需地砖数量与每块地砖的面积成反比例,因为每块地砖的面积与所需地砖数量的乘积都等于教室的面积,教室的面积一定。
9.食品加工厂准备把一批新酿的醋装瓶运往商店。
每瓶容量/mL
250
500
750
1500
所装瓶数/瓶
1200
600
400
200
所装瓶数与每瓶容量是否成反比例关系?为什么?
解:250×1200=300000(mL)=300(L) 500×600=300000(mL)=300(L)
750×400=300000(mL)=300(L) 1500×200=300000(mL)=300(L)
答:所装瓶数与每瓶容量成反比例,因为每瓶容量与所装瓶数的乘积是这批醋的体积(一定)。
10.下表中x和y两个量成反比例关系,请把表格填写完整。
x
2
100
40
12
y
5
50
0.1
11.判断下面各题中的两种量是否成反比例关系,并说明理由。
(1)煤的数量一定,使用天数与每天的平均用煤量。
(2)全班的人数一定,按各组人数相等的要求分组,组数与每组的人数。
(3)圆柱体积一定,圆柱的底面积与高。
(4)在一块菜地上种的黄瓜与西红柿的面积。
(5)书的总册数一定,按各包册数相等的规定包壮书,包数与每包的册数。
解:(1)因为每天的平均用煤量×使用天数=煤的数量(一定),所以使用天数与每天的平均用煤量成反比例关系。
(2)因为每组人数×组数=全班的人数(一定),所以组数与每组的人数成反比例关系。
(3)因为圆柱的底面积×高=圆柱的体积(一定),所以圆柱的底面积与高成反比例关系。
(4)因为种黄瓜的面积与种西红柿的面积的和一定,而他们的乘积不一定,所以种黄瓜的面积与种西红柿的面积不成反比例关系。
(5)因为每包的册数×包数=书的总册数(一定),所以包数与每包的册数成反比例关系。
12.一个手机组装车间要完成一批任务,每天组装手机的数量与需要的天数如下表。
每天组装的数量/部
500
600
800
1000
1200
时间/天
24
20
15
12
10
(1)每天组装的数量用p表示,需要的天数用t表示。你能用式子表示出p、t和组装的手机总数之间的关系吗?
(2)p与t成什么比例关系?
(3)如果这批组装任务需要8天完成。每天组装多少部手机?
解:(1)pt=500×24=600×20=12000
(2)p与t成成反比例关系
(3)12000÷8=1500(部)
答:每天组装1500部手机。
13.京沪高铁的火车平均行驶速度与行驶完全程所需时间如下表。
速度/(km/h)
270
260
250
200
180
150
...
时间/h
5
5.2
6.5
...
(1)京沪高铁全长多少千米?
(2)如果用v表示火车的平均速度,t表示驶完全程所需时间。t与v成什么比例关系?你能写出这个关系式吗?
(3)如果火车的平均速度为325千米/时,驶完全程需要多长时间?
解:(1)260×5=1300(km)
答:京沪高铁全长1300千米。
(2)t与v成反比例关系; vt=1300
(3)1300÷325=4(小时)
答:驶完全程需要4小时。
14.下面的图象表示斑马和长颈鹿的奔跑情况。
(1)斑马的奔跑路程与奔跑时间是否成正比例关系?长颈鹿呢?
(2)估计一下,两种动物18分钟各跑多少千米?
(3)从图象上看,斑马跑的快还是长颈鹿跑的快?
解:(1)斑马的奔跑路程与奔跑时间成正比例关系,长颈鹿的奔跑路程与奔跑时间也成正比例关系。
(2)斑马和长颈鹿18分钟分别跑21.6千米14.4千米。
(3)斑马跑的快。
15.*有x、y、z三个相关联的量,并有xy=z。
(1)当z一定时,x与y成_ 反_比例关系。
(2)当x一定时,z与y成__正____比例关系。
(3)当y一定时,z与x成___正___比例关系。
16.*一个长方形的面积是36cm,用x和y表示它的长和宽。y与x成什么比例关系?如果把它们的关系用图象表示出来,图象是一条直线吗?
解:y与x成反比例关系,图象不是一条直线。
