第6章 数据的分析单元检测A卷(含解析)
文档属性
| 名称 | 第6章 数据的分析单元检测A卷(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 513.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-12 00:00:00 | ||
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
第6章数据的分析单元检测A卷
班级__________姓名____________总分___________
一、选择题
1.X,X,…X的平均数为4,X,X…X的平均数为6,则X,X,…X,X…X的平均数为( )
A. 5 B. 4 C.3 D. 8
2.从鱼塘捕获同时放养的鲤鱼120条,从 ( http: / / www.21cnjy.com )中任选8条称得每条鱼的质量分别是:1.4,1.7,1.5,1.4,1.4,1.2,1.7,1.7(单位:千克),那么估计这120条鱼的总质量大约为( )
A. 180 B. 200 C. 18 D. 20
3.已知一组数据-2,-1,0, 6, 6, 20, 35,那么这组数据的中位数和众数分别是( )
A. 6和6 B. 3和6 C. 6和0 D. 9.5和6
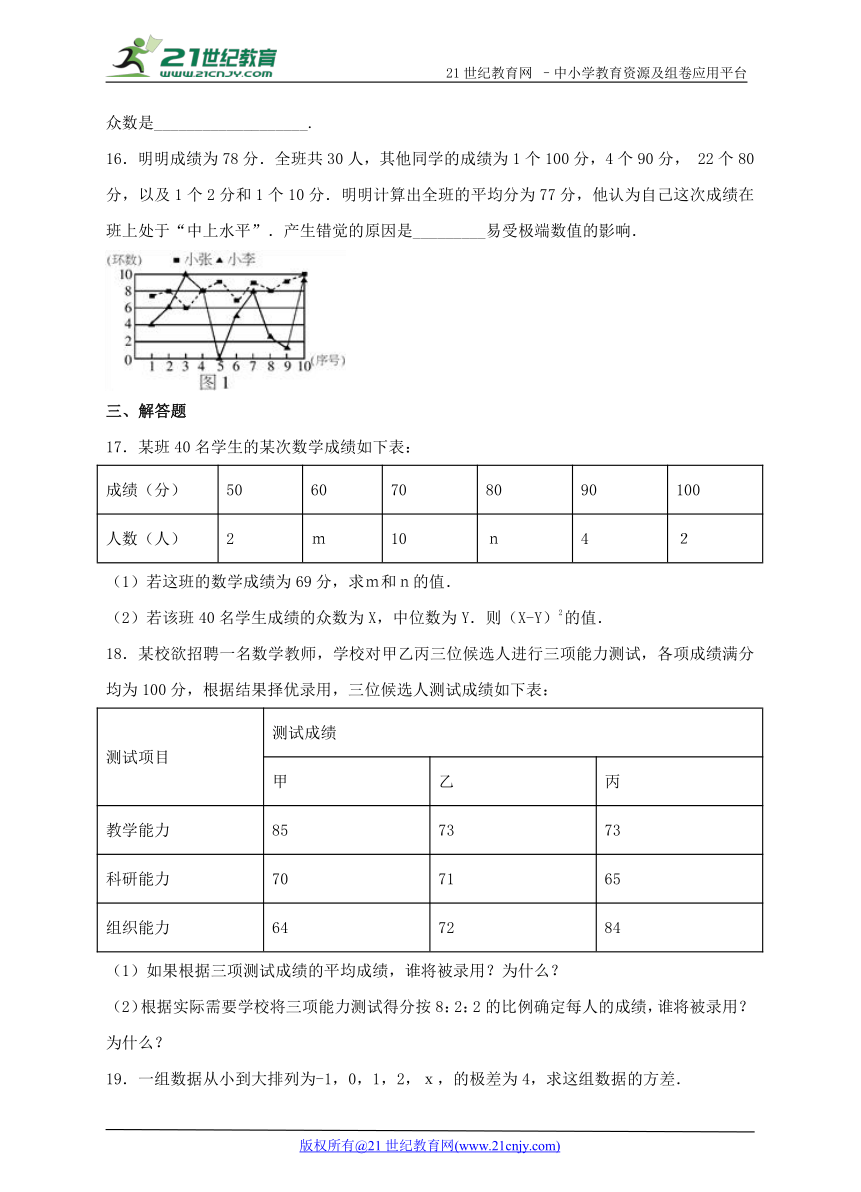
4.如图是甲、乙两组数据的折线统计图,下列结论中正确的是( )
( http: / / www.21cnjy.com )
A. 甲组数据比乙组数据稳定 B. 乙组数据比甲组数据稳定
C. 甲、乙两组数据一样稳定 D. 不能比较两组数据的稳定性
5.如果一组数据的方差是2,那么这一组数据都扩大2倍后所构成的新的数据的的方差为( )
A. 16 B. 8 C. 4 D. 2
6.某鞋商在进行市场占有率的调查时,他最关注的是( )
A. 鞋型号的平均数 B. 鞋型号的众数
C. 鞋型号的中位数 D. 最小的鞋型号
7.8名学生的平均成绩是x,如果另外2名学生每人得84分,那么整个组的平均成绩是( )
A. B. C. D.
8.某工厂为了选拔1名车工参加加工直径为10mm的精密零件的技术比赛,随机分别抽取甲、乙两名车工加工的5个零件,现测得的结果如下表,请你用计算器比较、的大小( )
甲 10.05 10.02 9.97 9.96 10
乙 10 10.01 10.02 9.97 10
A. B. C. D.
9.国家实行一系列“三农”优惠政策后,农民收入大幅度增加.某乡所辖村庄去年的年人均收入(单位:元)情况如下表:www-2-1-cnjy-com
年人均收入 3 500 3 700 3 800 3 900 4 500
村庄个数 1 1 3 3 1
该乡去年各村庄年人均收入的中位数是( )
A. 3 700元 B. 3 800元 C. 3 850元 D. 3 900元
10.衡量样本和总体的波动大小的特征数是( )
A. 平均数 B. 方差 C. 众数 D. 中位数
二、填空题
11.样本数据为3,6,a,4,2的平均数为5,则这个样本的方差为___________
12.一组数据,5,6,6,X的中位数与平均数相等,则X的值_________________.
13.一个样本的方差是,则这个样本的容量为___________,平均数为___________.【出处:21教育名师】
14.某日天气预报说今天 最高气温为8℃,气温的极差为9℃,则该日最低气温为_____________℃.【版权所有:21教育】
15.一组数据,-2 ,-2,3,-2,x ( http: / / www.21cnjy.com ),-1,它门的平均数为0.5,则它们的中位数是 _______________,众数是___________________.21教育名师原创作品
16.明明成绩为78分.全班共30人,其他 ( http: / / www.21cnjy.com )同学的成绩为1个100分,4个90分, 22个80分,以及1个2分和1个10分.明明计算出全班的平均分为77分,他认为自己这次成绩在班上处于“中上水平”.产生错觉的原因是_________易受极端数值的影响.
( http: / / www.21cnjy.com )
三、解答题
17.某班40名学生的某次数学成绩如下表:
成绩(分) 50 60 70 80 90 100
人数(人) 2 m 10 n 4 2
(1)若这班的数学成绩为69分,求m和n的值.
(2)若该班40名学生成绩的众数为X,中位数为Y.则(X-Y)2的值.
18.某校欲招聘一名数学教 ( http: / / www.21cnjy.com )师,学校对甲乙丙三位候选人进行三项能力测试,各项成绩满分均为100分,根据结果择优录用,三位候选人测试成绩如下表:www.21-cn-jy.com
测试项目 测试成绩
甲 乙 丙
教学能力 85 73 73
科研能力 70 71 65
组织能力 64 72 84
(1)如果根据三项测试成绩的平均成绩,谁将被录用?为什么?
(2)根据实际需要学校将三项能力测试得分按8:2:2的比例确定每人的成绩,谁将被录用?为什么?
19.一组数据从小到大排列为-1,0,1,2,x,的极差为4,求这组数据的方差.
20.阅读对学生的成长有着深远的影响, ( http: / / www.21cnjy.com )某中学为了解学生每周课余阅读的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表.
组别 时间(小时) 频数(人数) 频率
A 0≤t≤0.5 9 0.18
B 0.5≤t≤1 a 0.3
C 1≤t≤1.5 12 0.24
D 1.5≤t≤2 10 b
E 2≤t≤2.5 4 0.08
合计 1
( http: / / www.21cnjy.com )
请根据图表中的信息,解答下列问题:
(1)表中的a= ,b= ,中位数落在 组,将频数分布直方图补全;
(2)估计该校2000名学生中,每周课余阅读时间不足0.5小时的学生大约有多少名?
(3)E组的4人中,有1名男生和3 ( http: / / www.21cnjy.com )名女生,该校计划在E组学生中随机选出两人向全校同学作读书心得报告,请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率.21世纪教育网版权所有
21.某商贸公司有10名销售员,去年完成的销售情况如下表:
销售额(万元/单位) 3 4 5 6 7 8 10
销售人员(人/单位) 1 3 2 1 1 1 1
(1)求销售额的平均数,众数,中位数.
(2)今年公司为了调动员工的积极性 ( http: / / www.21cnjy.com )提高销售额 ,准备采取超额有将的措施,请你根据(1)得计算结果,通过比较,帮组公司领导确定今年每个销售人员统一的销售标准应是多少?为什么?21cnjy.com
22.甲乙两人在相同条件下射击,每人打5发子弹,命中环数如下:
甲:6,8,9,9,8
乙:10,7,7,7,9
问谁的射击成绩比较稳定?
23.某中学抽样调查后得到n名学生年龄情况,将结果绘制成如图的扇形统计图.
(1)被调查学生年龄的中位数是_______,众数是________;
(2)被调查的学生中12岁学生比16岁学生多30人,通过计算求14岁学生的人数;
(3)通过计算求该学校学生年龄的平均数(精确到1岁).
( http: / / www.21cnjy.com )
24.某校为选拨参加2005年全国初中数学竞 ( http: / / www.21cnjy.com )赛选手,进行了集体培训.在集训期间进行了10次测试,假设其中两位同学的测试成绩如下面的图表(如图)所示:
( http: / / www.21cnjy.com )
根据图表中的信息填写下表:
( http: / / www.21cnjy.com )
(2)这两位同学的测试成绩各有什么特点(从不同的角度分别说出一条即可)?
(3)为了使参赛选手取得好成绩,应该选谁参加比赛?为什么?
25.今年五一旅游黄金周期 ( http: / / www.21cnjy.com )间,某旅游区的开放时间为每天10小时,并每小时对进入旅游区的游客人数进行一次统计,下表是5月2日对进入旅游区人数的7次抽样统计数据.
记数的次数 第1次 第2次 第3次 第4次 第5次 第6次 第7次
每小时进入旅游区的人数 318 310 310 286 280 312 284
(1)旅游区平均每小时接纳游客多少人?
(2)若旅游区的门票为60元/张,则5月2日这一天门票收入是多少?
(3)据统计,5月1日至 ( http: / / www.21cnjy.com )5月5日,每天进入旅游区的人数相同,5月6日和5月7日这两天进入旅游区的人数分别比前一天减少10%和20%,那么从5月1日至5月7日旅游区门票收入是多少?21*cnjy*com
参考答案
1.A
【解析】根据题意可知:,,可求得=20,=30,因此可得.
故选:A.
2.A
【解析】根据8条鲤鱼的重量求得它们的平均重量为:=1. 5千克,所以估计这120条鱼的总质量为120×1. 5=180千克.21·cn·jy·com
故选:A.
3.A
【解析】要求一组数据的中位数,把这组数 ( http: / / www.21cnjy.com )据按照从小到大的顺序排列0,1,2,6,6,13,20,35,第4、5个两个数的平均数是(6+6)÷2=6,所以中位数是6,在这组数据中出现次数最多的是6,即众数是6.
故选:A.2·1·c·n·j·y
4.B
【解析】从图中可以看出:甲组数据的折线统计图起伏较大,所以甲组的数据不如乙组的数据稳定,故选B.
5.B
【解析】根据方差的公式S2= [(x1-)2+(x2-)2+…+(xn-)2],可知当每个数都扩大2倍后,平均数也扩大2倍,因此其方差变为2×2×2=8.【来源:21cnj*y.co*m】
故选:B.
点睛:此题主要考查了方差的计算,利用方差公式S2= [(x1-)2+(x2-)2+…+(xn-)2]代入计算即可判断.21*cnjy*com
6.B
【解析】由于众数是数据中出现最多的数,故鞋厂最关注的是销售量最多的鞋号即众数.
故选:B.
点评:本题考查学生对统计量的意义的理解与运用.要求学生对统计量进行合理的选择和恰当的运用.
7.D
【解析】先求这10个人的总成绩8x+2×84=8x+168,再除以10可求得平均值为:.
故选D.
8.A
【解析】甲的平均数=(10.05+10.02+9.97+9.96+10)÷5=10,
乙的平均数=(10+10.01+10.02+9.97+10)÷5=10;
S2甲=[(10.05-10)2+(10.02-10)2+(9.97-10)2+(9.96-10)2+(10-10)2]= ,
S2乙=[(10-10)2+(10.01-10)2+(10.02-10)2+(9.97-10)2+(10-10)2]= ;
故有S2甲>S2乙.
故选A.
9.B
【解析】根据图表可知题目中数据共有10个,
故中位数是按从小到大排列后第5,第6两个数的平均数作为中位数,
故这组数据的中位数是(3800+3800)=3800元.
故选B.
【点睛】主要运用了求中位数的方法,一些 ( http: / / www.21cnjy.com )学生往往对这个图表分析的不准确,没有考虑到共有8个数据而不是4个而错解.注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数.如果数据有奇数个,则正中间的数字即为所求;如果是偶数个,则找中间两位数的平均数.
10.B
【解析】根据方差的概念知,方差反映了一组数据的波动大小.
故选:B.
点睛:本题考查方差的定义与意义:一般地设n个数据,x1,x2,…xn的平均数为,则方差S2= [(x1-)2+(x2-)2+…+(xn-)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.2-1-c-n-j-y
11.8
【解析】根据平均数的意义,可知(3+6+a+4+2)=5,解得a=10,则根据方差公式可得这个样本的方差为:S2=[(3-5)2+(6-5)2+(10-5)2+(4-5)2+(2-5)2]=8.
故答案为:8.
12.5或7
【解析】根据平均数和中位数的概念,可知:
当x≥6时,中位数为6,平均数为,根据中位数和平均数相等,可得=6,解得x=7;
当5<x<6时,排列为5,x,6,6,中位数为(x+6),平均数为,根据中位数和平均数相等,可得(x+6)=,解得x=5,不在范围内,不正确;
当x≤5时,排列为5,5,6,6,中位数为(5+6)=5.5,平均数为,即=5.5,解得x=5.21教育网
故答案为为:5或7.
点睛:本题考查平均数和中位数.求一 ( http: / / www.21cnjy.com )组数据的中位数时,先将该组数据按从小到大(或按从大到小)的顺序排列,然后根据数据的个数确定中位数:当数据个数为奇数时,则中间的一个数即为这组数据的中位数;当数据个数为偶数时,则最中间的两个数的算术平均数即为这组数据的中位数.同时运用分类讨论的思想解决问题.
13.20;10
【解析】根据方差公式S2= [(x1-)2+(x2-)2+…+(xn-)2]中n表示样本容量,表示数据的平均数,故可知数据样本容量为20,平均数为10.
故答案为:20;10.
14.-1
【解析】根据极差的概念,最大值减去最小值,可知最低气温为:8-9=-1℃.
故答案为:-1.
15.-1.5, -2
【解析】据题意得(-2-2+3-2-x- ( http: / / www.21cnjy.com )1)÷6=-0.5,可得-x=1,所以将一组数据从小到大重新排列-2,-2,-2,-1,1,3,所以这组数据的最中间两个数是-2、-1,则这组数据的中位数是 -2-1 2 =-1.5;这组数据是(-2,-2,3,-2,1,-1),这组数据中出现次数最多的数是-2,所以这组数据的众数是-2.
故答案为:-1.5;-2.
16.平均数
【解析】共30人,将这组数据从小到大的顺序排列,处于中间位置的两个数都是80,
则这组数据的中位数是80.
故不是处在‘中上’水平.
她的这种想法是错误的,她的成绩在中位数以下, 他认为自己这次成绩在班上处于“中上水平”.产生错觉的原因是平均数易受极端数值的影响.21·世纪*教育网
【点睛】考查了确定一组数据的中位数的 ( http: / / www.21cnjy.com )能力.一些学生往往对这个概念掌握不清楚,计算方法不明确而误选其它选项,注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求,如果是偶数个则找中间两位数的平均数.
17.(1)m=18 n= 4;(2)x=60,y=65,=25.
【解析】试题分析:(1)根据题意可得两 ( http: / / www.21cnjy.com )个方程①50×2+60m+70×10+80n+90×4+100×2=69×40;②x+y+2+10+4+2=40,解方程组可得x、y的值;
(2)根据中位数以及众数的定义分别得出即可.
试题解析:(1)依题意:
解得 ,
(2)因为60出现次数最多,故 ( http: / / www.21cnjy.com )众数是:60分;
40个数据中最中间的是第20,21个数据,第20个数据为60,第21个数据为:70,
故中位数是:(60+70)÷2=65(分).
所以(x-y)2=25.
点睛:此题主要考查了二元一次方程组的应用以及中位数和众数的定义,学生要学会运用方程的思想解决问题.
18.详见解析.
【解析】试题分析:(1)运用求平均数公式即可求出三人的平均成绩,比较得出结果;
(2)将三人的总成绩按比例求出测试成绩,比较得出结果.
试题解析:(1)甲的平均成绩为:(85 ( http: / / www.21cnjy.com )+70+64)÷3=73,
乙的平均成绩为:(73+71+72)÷3=72,
丙的平均成绩为:(73+65+84)÷3=74,
∴丙的平均成绩最好,候选人丙将被录用;
(2)甲的测试成绩为:(85×5+70×3 ( http: / / www.21cnjy.com )+64×2)÷(5+3+2)=76.3,
乙的测试成绩为:(73×5+71×3+72×2)÷(5+3+2)=72.2,
丙的测试成绩为:(73×5+65×3+84×2)÷(5+3+2)=72.8,
∴甲的综合成绩最好,候选人甲将被录用.
点睛:本题是平均数的综合运用题.解题的关键是熟记平均数的概念.
19.详见解析.
【解析】试题分析:已知这组数据从小到大排列,根据极差的概念求出x,然后根据平均数公式和方差公式求出方差即可。
试题解析:已知这组数据从小到大排列,极差为4,所以x-(-1)=4,解得x=3,
求得平均数为:
所以方差为:S2= [(-1-1)2+(0-1)2+(1-1)2+(2-1)2+(3-1)2]=2.
20.(1)15,0.2(2)360(3)见解析
【解析】试题分析:(1)先求得抽取的学生数,再根据频率计算频数,根据频数计算频率;
(2)根据每周课余阅读时间不足0.5小时的学生的频率,估计该校2000名学生中,每周课余阅读时间不足0.5小时的学生数即可;
(3)通过画树状图,根据概率的计算公式,即可得到抽取的两名学生刚好是1名男生和1名女生的概率.
试题解析:(1)∵抽取的学生数为6÷0.15=40人,
∴a=0.3×40=12人,b=8÷40=0.2,
频数分布直方图如下:
( http: / / www.21cnjy.com )
(2)该校2000名学生中,每周课余阅读时间不足0.5小时的学生大约有:0.15×2000=300人;
(3)树状图如图所示:
( http: / / www.21cnjy.com )
总共有12种等可能的结果,其中刚好是1名男生和1名女生的结果有6种,
∴抽取的两名学生刚好是1名男生和1名女生的概率= ( http: / / www.21cnjy.com ).
考点:列表法与树状图法;用样本估计总体;频数(率)分布表;频数(率)分布直方图;中位数.
21.(1) 平均数5.6 ,众数4,中位数5;(2)详见解析.
【解析】试题分析:(1)根据 ( http: / / www.21cnjy.com )平均数、众数、中位数的意义与求法,易求得平均数、众数、中位数的值.
(2)确定今年每个销售人员统一的销售标准应是中位数.
试题解析:(1) 平均数5.6 众数4 中位数5
(2)今年每名销售人员统一标准是5万 ( http: / / www.21cnjy.com )元,理由如下:若规定平均数5.6万元为标准,则多数人(6名)无法或很难超额完成而得不到奖励,这样会挫伤员工的积极性,若规定众数4万元为标准,则绝大多数不需努力就可超额完成这不利于提高公司的年销售额,若定为5万元,大多数人可以完成或超额完成,少数人经过努力也能够完成这样就比较合理.
点睛:本题考查平均数、众数与中位数的意 ( http: / / www.21cnjy.com )义.
平均数是指在一组数据中所有数据之和再除以数据的个数.它是反映数据集中趋势的一项指标.
中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.
众数是数据中出现最多的一个数.
22.甲稳定,理由见解析.
【解析】试题分析:根据题意,分别计算甲乙两个人的方差可得,甲的方差小于乙的方差;结合方差的意义,可得甲比乙稳定.
试题解析:甲的平均数=(6+8+9+9+8)÷5=8
乙的平均数=(10+7+7+7+9)÷5=8
S甲2= [(6-8)2+(8-8)2+(9-8)2+(9-8)2+(8-8)2]=1.2
S乙2=[(10-8)2+(7-8)2+(7-8)2+(7-8)2+(9-8)2]=1.6
∵S甲2<S乙2
∴甲比乙稳定.
点睛:本题考查方差的定义与意义,明确方差的意义:一般地设n个数据,x1,x2,…xn的平均数为 ,则方差S2= [(x1-)2+(x2-)2+…+(xn-)2],先求出平均数及方差,再由方差反映一组数据的波动大小,方差越大,波动性越大,反之也成立,判断即可.
23. 14, 14;(2)240人;(3)14
【解析】试题分析:(1)根据中位数、众数 ( http: / / www.21cnjy.com )的定义解答;
(2)根据12岁学生比16岁学生多30人,列方程求解;
(3)利用加权平均数公式即可求解.
试题解析:
(1)中位数是14岁,众数是14岁;
(2)根据题意得10%n﹣(1﹣40%﹣20%﹣25%﹣10%)n=30,
解得:n=600,
则14岁学生的人数是240人;
(3)该校学生年龄的平均数是:5×20%+14×40%+13×25%+12×10%+16×5%≈14(岁).
24.(1)甲的中位数是94.5,乙的众数是99;
(2)答案不惟一,如,甲的成绩比乙的成绩稳定等;
(3)答案不惟一,如,应该选乙.
【解析】试题分析:(1)对甲的数据由小到大进 ( http: / / www.21cnjy.com )行整理,可得甲的中位数;可直接得到乙的众数;
(2)此题是开放题目,因此学生的回答是多样的,例如:甲考试成绩较稳定,因为方差,极差较小(或甲的平均数比乙的平均数高);乙有潜力,因为乙的最好成绩比甲的最好成绩高等;
(3)此题的选择也是不一的,例如:选甲,因为10次测验,甲有8次不少于90分,而乙仅有6次;选乙,因为乙有4次在99分以上.【来源:21·世纪·教育·网】
试题解析:
(1)甲的中位数=,乙的众数是99;
(2)从稳定性看:甲考试成绩较稳定, ( http: / / www.21cnjy.com )因为方差,极差较小;从平均数看:甲的平均数比乙的平均数高;乙有潜力,因为乙的最好成绩比甲的最好成绩高.从众数看:乙的成绩比甲好.从中位数看:甲比乙的成绩好.
(3)10次测验,甲有8次不少于90分,而乙仅有6次,若想获奖可能性较大,可选甲参赛;
若想拿到更好的名次可选乙,因为乙有4次在99分以上.
【点睛】本题考查的是条形统计图和表格的 ( http: / / www.21cnjy.com )综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键;除此之外,本题重点考查了运用平均数、中位数、众数和方差的意义解决问题的能力.
25.(1)300(人);(2)180 ( http: / / www.21cnjy.com )000(元);(3)5月1日至5月5日每天进入旅游区的人数为3000(人);5月6日进入旅游区的人数为2700(人);5月7日进入旅游区的人数为2160(人);5月1日至5月7日进入旅游区的人数共为19860(人);门票收入为1191600(元)
【解析】试题分析:(1)从表格中的 ( http: / / www.21cnjy.com )数据求出旅游区平均每小时接纳游客数;
(2)计算出5月2日这一天的接纳游客数,则5月2日这一天门票收入=游客数×门票价格
(3)分别计算出:5月1日至5月5日的收入,5月6日的收入,5月7日的收入,即可求得总收入.
试题解析:
(1)旅游区平均每小时接纳游客数= =300(人);
(2)5月2日这一天的接纳游客数=300×10=3000(人),
5月2日这一天门票收入=3000×60=180000(元);
(3)5月1日至5月5日的收入=180000×5=900000(元),
5月6日接纳游客数=3000×(1-10%)=2700(人),
5月6日的收入=2700×60=162000(元),
5月7日接纳游客数=2700×(1-20%)=2160(人),
5月7日的收入=2160×60=129600(元),
∴5月1日至5月7日的收入=900000+162000+129600=1191600(元).
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
第6章数据的分析单元检测A卷
班级__________姓名____________总分___________
一、选择题
1.X,X,…X的平均数为4,X,X…X的平均数为6,则X,X,…X,X…X的平均数为( )
A. 5 B. 4 C.3 D. 8
2.从鱼塘捕获同时放养的鲤鱼120条,从 ( http: / / www.21cnjy.com )中任选8条称得每条鱼的质量分别是:1.4,1.7,1.5,1.4,1.4,1.2,1.7,1.7(单位:千克),那么估计这120条鱼的总质量大约为( )
A. 180 B. 200 C. 18 D. 20
3.已知一组数据-2,-1,0, 6, 6, 20, 35,那么这组数据的中位数和众数分别是( )
A. 6和6 B. 3和6 C. 6和0 D. 9.5和6
4.如图是甲、乙两组数据的折线统计图,下列结论中正确的是( )
( http: / / www.21cnjy.com )
A. 甲组数据比乙组数据稳定 B. 乙组数据比甲组数据稳定
C. 甲、乙两组数据一样稳定 D. 不能比较两组数据的稳定性
5.如果一组数据的方差是2,那么这一组数据都扩大2倍后所构成的新的数据的的方差为( )
A. 16 B. 8 C. 4 D. 2
6.某鞋商在进行市场占有率的调查时,他最关注的是( )
A. 鞋型号的平均数 B. 鞋型号的众数
C. 鞋型号的中位数 D. 最小的鞋型号
7.8名学生的平均成绩是x,如果另外2名学生每人得84分,那么整个组的平均成绩是( )
A. B. C. D.
8.某工厂为了选拔1名车工参加加工直径为10mm的精密零件的技术比赛,随机分别抽取甲、乙两名车工加工的5个零件,现测得的结果如下表,请你用计算器比较、的大小( )
甲 10.05 10.02 9.97 9.96 10
乙 10 10.01 10.02 9.97 10
A. B. C. D.
9.国家实行一系列“三农”优惠政策后,农民收入大幅度增加.某乡所辖村庄去年的年人均收入(单位:元)情况如下表:www-2-1-cnjy-com
年人均收入 3 500 3 700 3 800 3 900 4 500
村庄个数 1 1 3 3 1
该乡去年各村庄年人均收入的中位数是( )
A. 3 700元 B. 3 800元 C. 3 850元 D. 3 900元
10.衡量样本和总体的波动大小的特征数是( )
A. 平均数 B. 方差 C. 众数 D. 中位数
二、填空题
11.样本数据为3,6,a,4,2的平均数为5,则这个样本的方差为___________
12.一组数据,5,6,6,X的中位数与平均数相等,则X的值_________________.
13.一个样本的方差是,则这个样本的容量为___________,平均数为___________.【出处:21教育名师】
14.某日天气预报说今天 最高气温为8℃,气温的极差为9℃,则该日最低气温为_____________℃.【版权所有:21教育】
15.一组数据,-2 ,-2,3,-2,x ( http: / / www.21cnjy.com ),-1,它门的平均数为0.5,则它们的中位数是 _______________,众数是___________________.21教育名师原创作品
16.明明成绩为78分.全班共30人,其他 ( http: / / www.21cnjy.com )同学的成绩为1个100分,4个90分, 22个80分,以及1个2分和1个10分.明明计算出全班的平均分为77分,他认为自己这次成绩在班上处于“中上水平”.产生错觉的原因是_________易受极端数值的影响.
( http: / / www.21cnjy.com )
三、解答题
17.某班40名学生的某次数学成绩如下表:
成绩(分) 50 60 70 80 90 100
人数(人) 2 m 10 n 4 2
(1)若这班的数学成绩为69分,求m和n的值.
(2)若该班40名学生成绩的众数为X,中位数为Y.则(X-Y)2的值.
18.某校欲招聘一名数学教 ( http: / / www.21cnjy.com )师,学校对甲乙丙三位候选人进行三项能力测试,各项成绩满分均为100分,根据结果择优录用,三位候选人测试成绩如下表:www.21-cn-jy.com
测试项目 测试成绩
甲 乙 丙
教学能力 85 73 73
科研能力 70 71 65
组织能力 64 72 84
(1)如果根据三项测试成绩的平均成绩,谁将被录用?为什么?
(2)根据实际需要学校将三项能力测试得分按8:2:2的比例确定每人的成绩,谁将被录用?为什么?
19.一组数据从小到大排列为-1,0,1,2,x,的极差为4,求这组数据的方差.
20.阅读对学生的成长有着深远的影响, ( http: / / www.21cnjy.com )某中学为了解学生每周课余阅读的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表.
组别 时间(小时) 频数(人数) 频率
A 0≤t≤0.5 9 0.18
B 0.5≤t≤1 a 0.3
C 1≤t≤1.5 12 0.24
D 1.5≤t≤2 10 b
E 2≤t≤2.5 4 0.08
合计 1
( http: / / www.21cnjy.com )
请根据图表中的信息,解答下列问题:
(1)表中的a= ,b= ,中位数落在 组,将频数分布直方图补全;
(2)估计该校2000名学生中,每周课余阅读时间不足0.5小时的学生大约有多少名?
(3)E组的4人中,有1名男生和3 ( http: / / www.21cnjy.com )名女生,该校计划在E组学生中随机选出两人向全校同学作读书心得报告,请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率.21世纪教育网版权所有
21.某商贸公司有10名销售员,去年完成的销售情况如下表:
销售额(万元/单位) 3 4 5 6 7 8 10
销售人员(人/单位) 1 3 2 1 1 1 1
(1)求销售额的平均数,众数,中位数.
(2)今年公司为了调动员工的积极性 ( http: / / www.21cnjy.com )提高销售额 ,准备采取超额有将的措施,请你根据(1)得计算结果,通过比较,帮组公司领导确定今年每个销售人员统一的销售标准应是多少?为什么?21cnjy.com
22.甲乙两人在相同条件下射击,每人打5发子弹,命中环数如下:
甲:6,8,9,9,8
乙:10,7,7,7,9
问谁的射击成绩比较稳定?
23.某中学抽样调查后得到n名学生年龄情况,将结果绘制成如图的扇形统计图.
(1)被调查学生年龄的中位数是_______,众数是________;
(2)被调查的学生中12岁学生比16岁学生多30人,通过计算求14岁学生的人数;
(3)通过计算求该学校学生年龄的平均数(精确到1岁).
( http: / / www.21cnjy.com )
24.某校为选拨参加2005年全国初中数学竞 ( http: / / www.21cnjy.com )赛选手,进行了集体培训.在集训期间进行了10次测试,假设其中两位同学的测试成绩如下面的图表(如图)所示:
( http: / / www.21cnjy.com )
根据图表中的信息填写下表:
( http: / / www.21cnjy.com )
(2)这两位同学的测试成绩各有什么特点(从不同的角度分别说出一条即可)?
(3)为了使参赛选手取得好成绩,应该选谁参加比赛?为什么?
25.今年五一旅游黄金周期 ( http: / / www.21cnjy.com )间,某旅游区的开放时间为每天10小时,并每小时对进入旅游区的游客人数进行一次统计,下表是5月2日对进入旅游区人数的7次抽样统计数据.
记数的次数 第1次 第2次 第3次 第4次 第5次 第6次 第7次
每小时进入旅游区的人数 318 310 310 286 280 312 284
(1)旅游区平均每小时接纳游客多少人?
(2)若旅游区的门票为60元/张,则5月2日这一天门票收入是多少?
(3)据统计,5月1日至 ( http: / / www.21cnjy.com )5月5日,每天进入旅游区的人数相同,5月6日和5月7日这两天进入旅游区的人数分别比前一天减少10%和20%,那么从5月1日至5月7日旅游区门票收入是多少?21*cnjy*com
参考答案
1.A
【解析】根据题意可知:,,可求得=20,=30,因此可得.
故选:A.
2.A
【解析】根据8条鲤鱼的重量求得它们的平均重量为:=1. 5千克,所以估计这120条鱼的总质量为120×1. 5=180千克.21·cn·jy·com
故选:A.
3.A
【解析】要求一组数据的中位数,把这组数 ( http: / / www.21cnjy.com )据按照从小到大的顺序排列0,1,2,6,6,13,20,35,第4、5个两个数的平均数是(6+6)÷2=6,所以中位数是6,在这组数据中出现次数最多的是6,即众数是6.
故选:A.2·1·c·n·j·y
4.B
【解析】从图中可以看出:甲组数据的折线统计图起伏较大,所以甲组的数据不如乙组的数据稳定,故选B.
5.B
【解析】根据方差的公式S2= [(x1-)2+(x2-)2+…+(xn-)2],可知当每个数都扩大2倍后,平均数也扩大2倍,因此其方差变为2×2×2=8.【来源:21cnj*y.co*m】
故选:B.
点睛:此题主要考查了方差的计算,利用方差公式S2= [(x1-)2+(x2-)2+…+(xn-)2]代入计算即可判断.21*cnjy*com
6.B
【解析】由于众数是数据中出现最多的数,故鞋厂最关注的是销售量最多的鞋号即众数.
故选:B.
点评:本题考查学生对统计量的意义的理解与运用.要求学生对统计量进行合理的选择和恰当的运用.
7.D
【解析】先求这10个人的总成绩8x+2×84=8x+168,再除以10可求得平均值为:.
故选D.
8.A
【解析】甲的平均数=(10.05+10.02+9.97+9.96+10)÷5=10,
乙的平均数=(10+10.01+10.02+9.97+10)÷5=10;
S2甲=[(10.05-10)2+(10.02-10)2+(9.97-10)2+(9.96-10)2+(10-10)2]= ,
S2乙=[(10-10)2+(10.01-10)2+(10.02-10)2+(9.97-10)2+(10-10)2]= ;
故有S2甲>S2乙.
故选A.
9.B
【解析】根据图表可知题目中数据共有10个,
故中位数是按从小到大排列后第5,第6两个数的平均数作为中位数,
故这组数据的中位数是(3800+3800)=3800元.
故选B.
【点睛】主要运用了求中位数的方法,一些 ( http: / / www.21cnjy.com )学生往往对这个图表分析的不准确,没有考虑到共有8个数据而不是4个而错解.注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数.如果数据有奇数个,则正中间的数字即为所求;如果是偶数个,则找中间两位数的平均数.
10.B
【解析】根据方差的概念知,方差反映了一组数据的波动大小.
故选:B.
点睛:本题考查方差的定义与意义:一般地设n个数据,x1,x2,…xn的平均数为,则方差S2= [(x1-)2+(x2-)2+…+(xn-)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.2-1-c-n-j-y
11.8
【解析】根据平均数的意义,可知(3+6+a+4+2)=5,解得a=10,则根据方差公式可得这个样本的方差为:S2=[(3-5)2+(6-5)2+(10-5)2+(4-5)2+(2-5)2]=8.
故答案为:8.
12.5或7
【解析】根据平均数和中位数的概念,可知:
当x≥6时,中位数为6,平均数为,根据中位数和平均数相等,可得=6,解得x=7;
当5<x<6时,排列为5,x,6,6,中位数为(x+6),平均数为,根据中位数和平均数相等,可得(x+6)=,解得x=5,不在范围内,不正确;
当x≤5时,排列为5,5,6,6,中位数为(5+6)=5.5,平均数为,即=5.5,解得x=5.21教育网
故答案为为:5或7.
点睛:本题考查平均数和中位数.求一 ( http: / / www.21cnjy.com )组数据的中位数时,先将该组数据按从小到大(或按从大到小)的顺序排列,然后根据数据的个数确定中位数:当数据个数为奇数时,则中间的一个数即为这组数据的中位数;当数据个数为偶数时,则最中间的两个数的算术平均数即为这组数据的中位数.同时运用分类讨论的思想解决问题.
13.20;10
【解析】根据方差公式S2= [(x1-)2+(x2-)2+…+(xn-)2]中n表示样本容量,表示数据的平均数,故可知数据样本容量为20,平均数为10.
故答案为:20;10.
14.-1
【解析】根据极差的概念,最大值减去最小值,可知最低气温为:8-9=-1℃.
故答案为:-1.
15.-1.5, -2
【解析】据题意得(-2-2+3-2-x- ( http: / / www.21cnjy.com )1)÷6=-0.5,可得-x=1,所以将一组数据从小到大重新排列-2,-2,-2,-1,1,3,所以这组数据的最中间两个数是-2、-1,则这组数据的中位数是 -2-1 2 =-1.5;这组数据是(-2,-2,3,-2,1,-1),这组数据中出现次数最多的数是-2,所以这组数据的众数是-2.
故答案为:-1.5;-2.
16.平均数
【解析】共30人,将这组数据从小到大的顺序排列,处于中间位置的两个数都是80,
则这组数据的中位数是80.
故不是处在‘中上’水平.
她的这种想法是错误的,她的成绩在中位数以下, 他认为自己这次成绩在班上处于“中上水平”.产生错觉的原因是平均数易受极端数值的影响.21·世纪*教育网
【点睛】考查了确定一组数据的中位数的 ( http: / / www.21cnjy.com )能力.一些学生往往对这个概念掌握不清楚,计算方法不明确而误选其它选项,注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数,如果数据有奇数个,则正中间的数字即为所求,如果是偶数个则找中间两位数的平均数.
17.(1)m=18 n= 4;(2)x=60,y=65,=25.
【解析】试题分析:(1)根据题意可得两 ( http: / / www.21cnjy.com )个方程①50×2+60m+70×10+80n+90×4+100×2=69×40;②x+y+2+10+4+2=40,解方程组可得x、y的值;
(2)根据中位数以及众数的定义分别得出即可.
试题解析:(1)依题意:
解得 ,
(2)因为60出现次数最多,故 ( http: / / www.21cnjy.com )众数是:60分;
40个数据中最中间的是第20,21个数据,第20个数据为60,第21个数据为:70,
故中位数是:(60+70)÷2=65(分).
所以(x-y)2=25.
点睛:此题主要考查了二元一次方程组的应用以及中位数和众数的定义,学生要学会运用方程的思想解决问题.
18.详见解析.
【解析】试题分析:(1)运用求平均数公式即可求出三人的平均成绩,比较得出结果;
(2)将三人的总成绩按比例求出测试成绩,比较得出结果.
试题解析:(1)甲的平均成绩为:(85 ( http: / / www.21cnjy.com )+70+64)÷3=73,
乙的平均成绩为:(73+71+72)÷3=72,
丙的平均成绩为:(73+65+84)÷3=74,
∴丙的平均成绩最好,候选人丙将被录用;
(2)甲的测试成绩为:(85×5+70×3 ( http: / / www.21cnjy.com )+64×2)÷(5+3+2)=76.3,
乙的测试成绩为:(73×5+71×3+72×2)÷(5+3+2)=72.2,
丙的测试成绩为:(73×5+65×3+84×2)÷(5+3+2)=72.8,
∴甲的综合成绩最好,候选人甲将被录用.
点睛:本题是平均数的综合运用题.解题的关键是熟记平均数的概念.
19.详见解析.
【解析】试题分析:已知这组数据从小到大排列,根据极差的概念求出x,然后根据平均数公式和方差公式求出方差即可。
试题解析:已知这组数据从小到大排列,极差为4,所以x-(-1)=4,解得x=3,
求得平均数为:
所以方差为:S2= [(-1-1)2+(0-1)2+(1-1)2+(2-1)2+(3-1)2]=2.
20.(1)15,0.2(2)360(3)见解析
【解析】试题分析:(1)先求得抽取的学生数,再根据频率计算频数,根据频数计算频率;
(2)根据每周课余阅读时间不足0.5小时的学生的频率,估计该校2000名学生中,每周课余阅读时间不足0.5小时的学生数即可;
(3)通过画树状图,根据概率的计算公式,即可得到抽取的两名学生刚好是1名男生和1名女生的概率.
试题解析:(1)∵抽取的学生数为6÷0.15=40人,
∴a=0.3×40=12人,b=8÷40=0.2,
频数分布直方图如下:
( http: / / www.21cnjy.com )
(2)该校2000名学生中,每周课余阅读时间不足0.5小时的学生大约有:0.15×2000=300人;
(3)树状图如图所示:
( http: / / www.21cnjy.com )
总共有12种等可能的结果,其中刚好是1名男生和1名女生的结果有6种,
∴抽取的两名学生刚好是1名男生和1名女生的概率= ( http: / / www.21cnjy.com ).
考点:列表法与树状图法;用样本估计总体;频数(率)分布表;频数(率)分布直方图;中位数.
21.(1) 平均数5.6 ,众数4,中位数5;(2)详见解析.
【解析】试题分析:(1)根据 ( http: / / www.21cnjy.com )平均数、众数、中位数的意义与求法,易求得平均数、众数、中位数的值.
(2)确定今年每个销售人员统一的销售标准应是中位数.
试题解析:(1) 平均数5.6 众数4 中位数5
(2)今年每名销售人员统一标准是5万 ( http: / / www.21cnjy.com )元,理由如下:若规定平均数5.6万元为标准,则多数人(6名)无法或很难超额完成而得不到奖励,这样会挫伤员工的积极性,若规定众数4万元为标准,则绝大多数不需努力就可超额完成这不利于提高公司的年销售额,若定为5万元,大多数人可以完成或超额完成,少数人经过努力也能够完成这样就比较合理.
点睛:本题考查平均数、众数与中位数的意 ( http: / / www.21cnjy.com )义.
平均数是指在一组数据中所有数据之和再除以数据的个数.它是反映数据集中趋势的一项指标.
中位数是将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(最中间两个数的平均数),叫做这组数据的中位数.
众数是数据中出现最多的一个数.
22.甲稳定,理由见解析.
【解析】试题分析:根据题意,分别计算甲乙两个人的方差可得,甲的方差小于乙的方差;结合方差的意义,可得甲比乙稳定.
试题解析:甲的平均数=(6+8+9+9+8)÷5=8
乙的平均数=(10+7+7+7+9)÷5=8
S甲2= [(6-8)2+(8-8)2+(9-8)2+(9-8)2+(8-8)2]=1.2
S乙2=[(10-8)2+(7-8)2+(7-8)2+(7-8)2+(9-8)2]=1.6
∵S甲2<S乙2
∴甲比乙稳定.
点睛:本题考查方差的定义与意义,明确方差的意义:一般地设n个数据,x1,x2,…xn的平均数为 ,则方差S2= [(x1-)2+(x2-)2+…+(xn-)2],先求出平均数及方差,再由方差反映一组数据的波动大小,方差越大,波动性越大,反之也成立,判断即可.
23. 14, 14;(2)240人;(3)14
【解析】试题分析:(1)根据中位数、众数 ( http: / / www.21cnjy.com )的定义解答;
(2)根据12岁学生比16岁学生多30人,列方程求解;
(3)利用加权平均数公式即可求解.
试题解析:
(1)中位数是14岁,众数是14岁;
(2)根据题意得10%n﹣(1﹣40%﹣20%﹣25%﹣10%)n=30,
解得:n=600,
则14岁学生的人数是240人;
(3)该校学生年龄的平均数是:5×20%+14×40%+13×25%+12×10%+16×5%≈14(岁).
24.(1)甲的中位数是94.5,乙的众数是99;
(2)答案不惟一,如,甲的成绩比乙的成绩稳定等;
(3)答案不惟一,如,应该选乙.
【解析】试题分析:(1)对甲的数据由小到大进 ( http: / / www.21cnjy.com )行整理,可得甲的中位数;可直接得到乙的众数;
(2)此题是开放题目,因此学生的回答是多样的,例如:甲考试成绩较稳定,因为方差,极差较小(或甲的平均数比乙的平均数高);乙有潜力,因为乙的最好成绩比甲的最好成绩高等;
(3)此题的选择也是不一的,例如:选甲,因为10次测验,甲有8次不少于90分,而乙仅有6次;选乙,因为乙有4次在99分以上.【来源:21·世纪·教育·网】
试题解析:
(1)甲的中位数=,乙的众数是99;
(2)从稳定性看:甲考试成绩较稳定, ( http: / / www.21cnjy.com )因为方差,极差较小;从平均数看:甲的平均数比乙的平均数高;乙有潜力,因为乙的最好成绩比甲的最好成绩高.从众数看:乙的成绩比甲好.从中位数看:甲比乙的成绩好.
(3)10次测验,甲有8次不少于90分,而乙仅有6次,若想获奖可能性较大,可选甲参赛;
若想拿到更好的名次可选乙,因为乙有4次在99分以上.
【点睛】本题考查的是条形统计图和表格的 ( http: / / www.21cnjy.com )综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键;除此之外,本题重点考查了运用平均数、中位数、众数和方差的意义解决问题的能力.
25.(1)300(人);(2)180 ( http: / / www.21cnjy.com )000(元);(3)5月1日至5月5日每天进入旅游区的人数为3000(人);5月6日进入旅游区的人数为2700(人);5月7日进入旅游区的人数为2160(人);5月1日至5月7日进入旅游区的人数共为19860(人);门票收入为1191600(元)
【解析】试题分析:(1)从表格中的 ( http: / / www.21cnjy.com )数据求出旅游区平均每小时接纳游客数;
(2)计算出5月2日这一天的接纳游客数,则5月2日这一天门票收入=游客数×门票价格
(3)分别计算出:5月1日至5月5日的收入,5月6日的收入,5月7日的收入,即可求得总收入.
试题解析:
(1)旅游区平均每小时接纳游客数= =300(人);
(2)5月2日这一天的接纳游客数=300×10=3000(人),
5月2日这一天门票收入=3000×60=180000(元);
(3)5月1日至5月5日的收入=180000×5=900000(元),
5月6日接纳游客数=3000×(1-10%)=2700(人),
5月6日的收入=2700×60=162000(元),
5月7日接纳游客数=2700×(1-20%)=2160(人),
5月7日的收入=2160×60=129600(元),
∴5月1日至5月7日的收入=900000+162000+129600=1191600(元).
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
