第5章 数据的频数分布单元检测卷(含解析)
文档属性
| 名称 | 第5章 数据的频数分布单元检测卷(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 606.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-12 10:14:27 | ||
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
第5章 数据的频数分布单元检测卷
班级__________姓名____________总分___________
一、选择题
1.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其他完全相同小张通过多次摸球试验后发现,其中摸到红色、黑色球的频率稳定在和,则口袋中白色球的个数很可能是( )
A. 6 B. 16 C. 18 D. 24
2.在频数分布直方图中,各小长方形的高等于相应组的( )
A. 组距 B. 组数 C. 频数 D. 频率
3.袋子里有4个黑球,m个白球,它们除颜色外都相同,经过大量实验,从中任取一个球恰好是白球的频率是0.20,则m的值是( )
A. 1 B. 2 C. 4 D. 16
4.某校对 EMBED Equation.DSMT4 名女生的身高进行了测量,身高在 (单位: )这一小组的频率为 ,则该组的人数为 ( )
A. 人 B. 人 C. 人 D. 人
5.调查某班 EMBED Equation.DSMT4 名同学的跳高成绩时,在收集到的数据中,不足 米的数出现的频率是 ,则达到或超过 米的数出现的频率是 ( )
A. B. C. D.
6.一个容量为 EMBED Equation.DSMT4 的样本最大值为 ,最小值 ,取组距为 ,则可以分成 ( )
A. 组 B. 组 C. 组 D. 组
7.在统计中频率分布的主要作用是( )
A. 可以反映一组数据的波动大小 B. 可以反映一组数据的平均水平
C. 可以反映一组数据的分布情况 D. 可以看出一组数据的最大值和最小值
8.为了筹备班级联欢会,班长对全班50名同学喜欢吃哪几种水果作了民意调查,小明将班长的统计结果绘成如图的统计图,并得出四个结论,其中错误的是( )
A. 一个人可以喜欢吃几种水果
B. 喜欢吃葡萄的人最多
C. 喜欢吃苹果的人数是喜欢吃梨的人数的3倍
D. 喜欢吃香蕉的人数占全班人数的20%
9.将50个数据分成3组,其中第一组和第三组的频率之和为0.7,则第二小组的频数是( )
A. 0.3 B. 30 C. 15 D. 35
10.投掷硬币m次,正面向上n次,其频率p= EMBED Equation.DSMT4 ,则下列说法正确的是( )
A. p一定等于 B. p一定不等于
C. 多投一次,p更接近 D. 投掷次数逐步增加,p稳定在附近
11.在一个不透明的口袋里装着只有颜色不同的黑、白两种颜色的球共50只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复以上步骤,下表为实验的一组统计数据:
摸球的次数n 1000 1500 2000 5000 8000 10000
摸到白球的次数m 582 960 1161 2954 4842 6010
摸到白球的频率 0.582 0.64 0.5805 0.5908 0.6053 0.601
请估算口袋中白球的个数约为( )
A. 20 B. 25 C. 30 D. 35
12.某班50名学生期末考试数学成绩(单位:分)的频率分布直方图如图所示,其中数据不在分点上,对图中提供的信息作出如下的判断:
(1)成绩在49.5分~59.5分段的人数与89.5分~100分段的人数相等;
(2)成绩在79.5~89.5分段的人数占30%;
(3)成绩在79.5分以上的学生有20人;
(4)本次考试成绩的中位数落在69.5~79.5分段内.
其中正确的判断有( )
A. 4个 B. 3个 C. 2个 D. 1个
二、填空题
13.小强调查“每人每天的用水量”这一问题时,收集到80个数据,最大数据是70升,最小数据是42升,若取组距为4,则应分为_________组绘制频数分布表.
14.某中学对七年级女生仰卧起坐的测试成绩进行统计分析,将数据整理后,画出频数分布直方图(如图).已知图中从左到右的第一、第二、第三、第四、第六小组的百分比依次是10%,15%,20%,30%,5%,第五小组的频数是36,则参加这次测试的女生人数是____;若次数在24次(含24次)以上为达标,则该校七年级女生的达标率为______.
15.七年级一班共有48名学生,他们身高的频数分布直方图如图,各小长方形的高的比为1∶1∶3∶2∶1,则身高范围在__________________的学生最多,是____人.
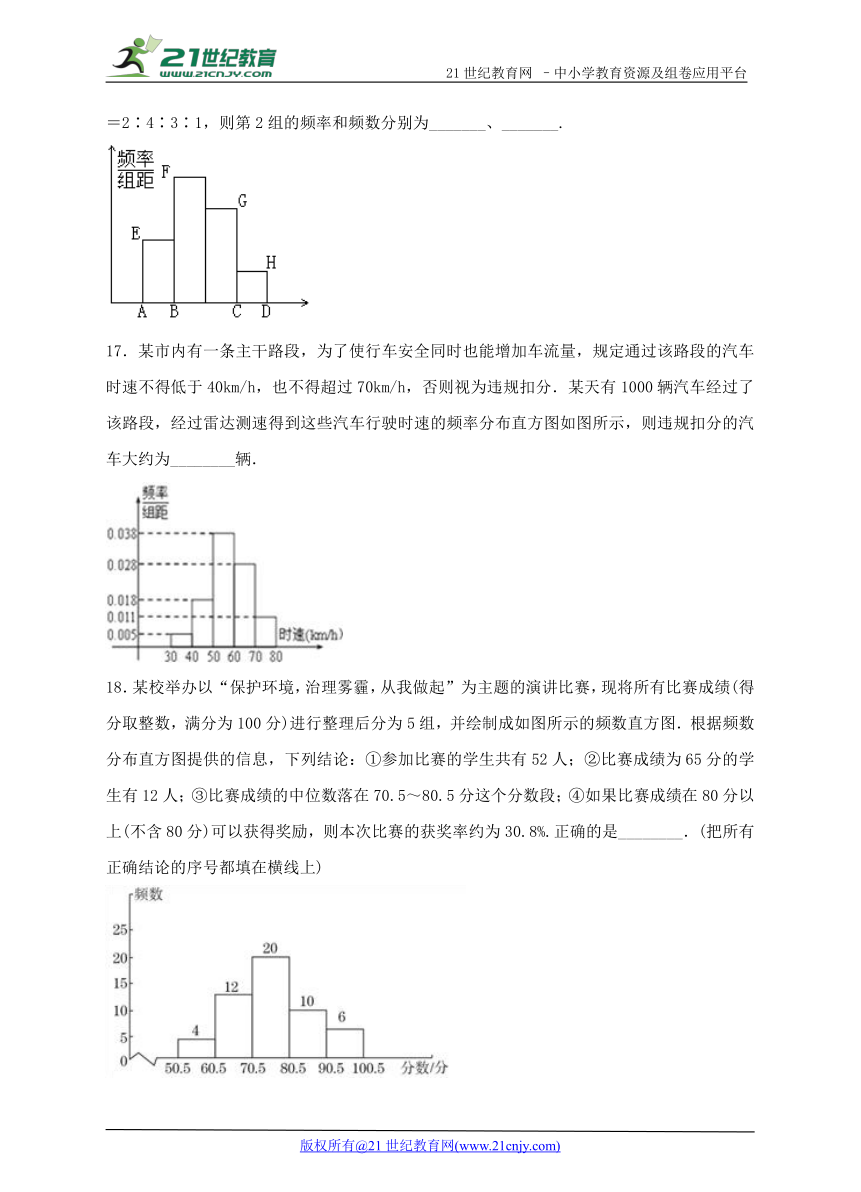
16.已知样本容量为30,在以下样本频率分布直方图中,各小长方形的高之比AE∶BF∶CG∶DH=2∶4∶3∶1,则第2组的频率和频数分别为_______、_______.
17.某市内有一条主干路段,为了使行车安全同时也能增加车流量,规定通过该路段的汽车时速不得低于40km/h,也不得超过70km/h,否则视为违规扣分.某天有1000辆汽车经过了该路段,经过雷达测速得到这些汽车行驶时速的频率分布直方图如图所示,则违规扣分的汽车大约为________辆.
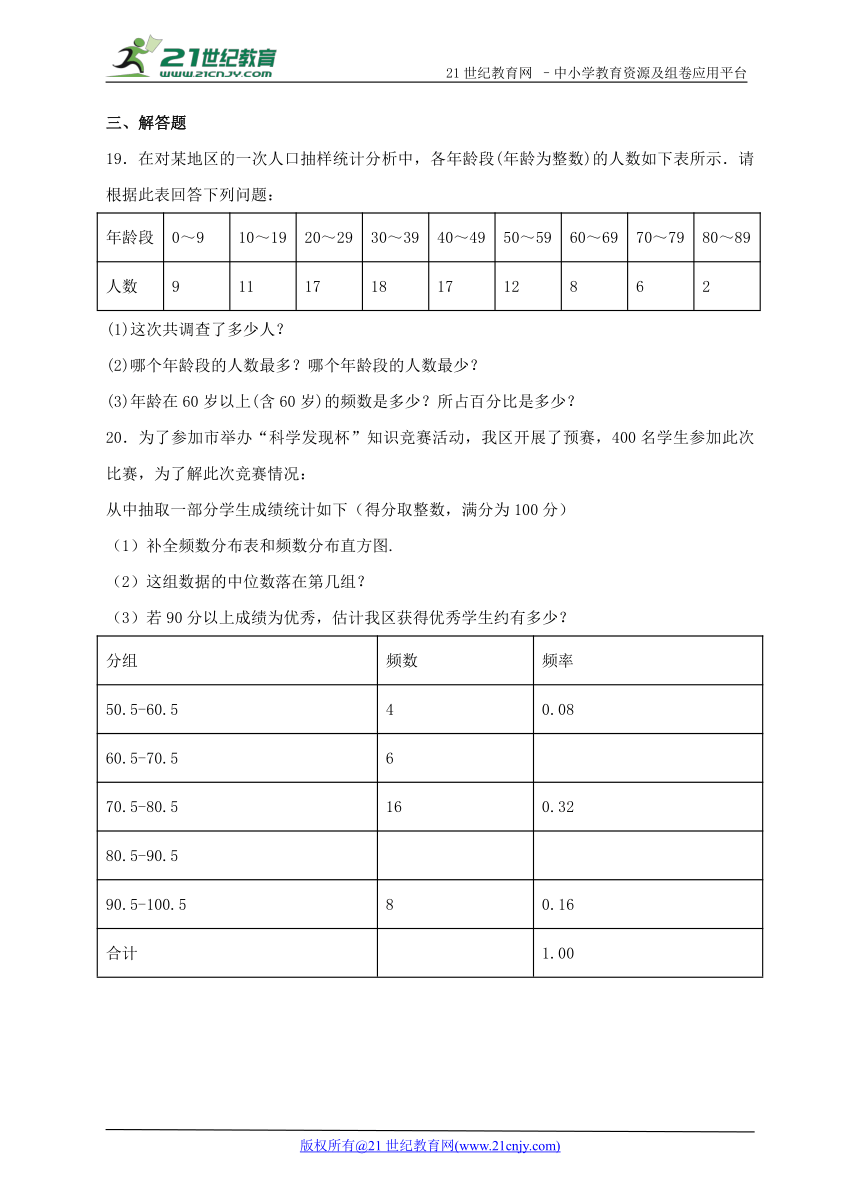
18.某校举办以“保护环境,治理雾霾,从我做起”为主题的演讲比赛,现将所有比赛成绩(得分取整数,满分为100分)进行整理后分为5组,并绘制成如图所示的频数直方图.根据频数分布直方图提供的信息,下列结论:①参加比赛的学生共有52人;②比赛成绩为65分的学生有12人;③比赛成绩的中位数落在70.5~80.5分这个分数段;④如果比赛成绩在80分以上(不含80分)可以获得奖励,则本次比赛的获奖率约为30.8%.正确的是________.(把所有正确结论的序号都填在横线上)
三、解答题
19.在对某地区的一次人口抽样统计分析中,各年龄段(年龄为整数)的人数如下表所示.请根据此表回答下列问题:
年龄段 0~9 10~19 20~29 30~39 40~49 50~59 60~69 70~79 80~89
人数 9 11 17 18 17 12 8 6 2
(1)这次共调查了多少人?
(2)哪个年龄段的人数最多?哪个年龄段的人数最少?
(3)年龄在60岁以上(含60岁)的频数是多少?所占百分比是多少?
20.为了参加市举办“科学发现杯”知识竞赛活动,我区开展了预赛,400名学生参加此次比赛,为了解此次竞赛情况:
从中抽取一部分学生成绩统计如下(得分取整数,满分为100分)
(1)补全频数分布表和频数分布直方图.
(2)这组数据的中位数落在第几组?
(3)若90分以上成绩为优秀,估计我区获得优秀学生约有多少?
分组 频数 频率
50.5-60.5 4 0.08
60.5-70.5 6
70.5-80.5 16 0.32
80.5-90.5
90.5-100.5 8 0.16
合计 1.00
21.4月23日是“世界读书日”,学校开展“让书香溢满校园”读书活动,以提升青少年的阅读兴趣,九年级(1)班数学活动小组对本年级600名学生每天阅读时间进行了统计,根据所得数据绘制了如图所示的两幅不完整的统计图(每组包括最小值不包括最大值)九年级(1)班每天阅读时间在0.5 h以内的学生占全班人数的8%,根据统计图解答下列问题:
(1)九年级(1)班有________名学生.
(2)补全频数分布直方图.
(3)除九年级(1)班外,九年级其他班级每天阅读时间为1~1.5 h的学生有165人,请你补全扇形统计图.
(4)求该年级每天阅读时间不少于1 h的学生有多少人.
22.小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
月均用水量/t 频数 百分比
2≤x<3 2 4%
3≤x<4 12 24%
4≤x<5
5≤x<6 10 20%
6≤x<7 12%
7≤x<8 3 6%
8≤x<9 2 4%
(2)如果家庭月均用水量“大于或等于4 t且小于7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.
23.为弘扬中华传统文化,某校组织八年级1000名学生参加汉字听写大赛,为了解学生整体听写能力,从中抽取部分学生的成绩(得分取正整数,满分为100分)进行统计分析,请根据尚未完成的下列图表,解答问题:
组别 分数段 频数 频率
一 50.5~60.5 16 0.08
二 60.5~70.5 30 0.15
三 70.5~80.5 50 0.25
四 80.5~90.5 m 0.40
五 90.5~100.5 n
(1)本次抽样调查的样本是__________________,样本容量为________,表中m=________,n=________;
(2)补全频数分布直方图;
(3)若抽取的样本具有较好的代表性,且成绩超过80分为优秀,根据样本估计该校八年级学生中汉字听写能力优秀的约有多少人?
24.为了解上一次八年级数学测验成绩情况,随机抽取了40名学生的成绩进行统计分析,这40名学生的成绩数据如下:
55 62 67 53 58 83 87 64 68 85
60 94 81 98 51 83 78 77 66 71
91 72 63 75 88 73 52 71 79 63
74 67 78 61 97 76 72 77 79 71
(1)将样本数据适当分组,制作频数分布表:
分 组
频 数
(2)根据频数分布表,绘制频数直方图:
(3)从图可以看出,这40名学生的成绩都分布在什么范围内?分数在哪个范围的人数最多?
25.为了解某校学生的身高情况,随机抽取该校若干男生、女生进行抽样调查.已知抽取的样本中,男生、女生人数相同,利用所得数据绘制如下统计表和统计图(如图20-3-2所示):
身高情况分组表(单位:cm)
组别 身高
A x<155
B 155≤x<160
C 160≤x<165
D 165≤x<170
E x≥170
根据图表提供的信息,回答下列问题:
(1)样本中,男生身高的众数在___________组,中位数在___________组;
(2)样本中,女生身高在E组的有___________人;
(3)已知该校共有男生400人、女生380人,请估计身高在160≤x<170范围内的学生约有多少人.
26.某年级组织学生参加夏令营,分为甲、乙、丙三组进行活动.下面两幅统计图反映了学生报名参加夏令营的情况.请你根据图中的信息回答下列问题:
报名人数分布直方图 报名人数扇形统计图
(1)求该年级报名参加本次活动的总人数;
(2)求该年级报名参加乙组的人数,并补全频数分布直方图;
(3)根据实际情况,需从甲组抽调部分同学到丙组,使丙组人数是甲组人数的3倍,那么,应从甲组抽调多少名学生到丙组?
参考答案
1.B
【解析】试题解析: 根据红色、黑色球的频率稳定在15%和45%,那么白色玻璃球出现的频率为1-15%-45%=40%,
根据多次实验中,可用一个事件发生的频率作为这个事件的概率的估计值,那么袋中有白色球的概率为
故口袋中白色球的个数为
故选B.
2.C
【解析】试题解析:在频数分布直方图中,每个小长方形的高等于每小组的频数.
故选C.
3.A
【解析】试题解析:袋子里有4个黑球,m个白球,若从中任取一个球恰好是白球的概率是
根据题意可得:
解得m=1.
故选A.
4.B
【解析】试题解析:根据题意,得
该组的人数为1200×0.25=300(人).
故选B.
5.B
【解析】试题解析:在收集到的数据中,不足 米的数出现的频率是 ,
则达到或超过 米的数出现的频率是:
故选B.
6.B
【解析】试题解析:最大值与最小值的差为:
因为
所以分成9组较为恰当.
故选B.
7.C
【解析】由平均数、方差的概念,可知它们分别反映总体的平均水平和波动大小,故A、B不正确;
根据统计中,频率是指每个对象出现的次数与总次数的比值(或百分比),频率反映了个组频数的大小在总数中所占的分量,即可以反映总体的分布情况.
故选:C.
点睛:本题考查了频率的意义,一般称落在不同小组中的数据个数为该组的频数,频数与数据总数的比值为频率.
8.D
【解析】30+10+20+40=100>50,所以一个人可以喜欢吃几种水果,故A选项正确;
喜欢吃葡萄的最多,为40人,故B选项正确;
喜欢吃苹果的有30人,喜欢吃梨的有10人,喜欢吃苹果的人数是喜欢吃梨的人数的3倍,故C选项正确;
喜欢吃香蕉的有20人,占全班总人数的:20÷50=40%,故D选项错误.
故选D.
点睛:掌握条形统计图.
9.C
【解析】根据频率的性质,各组的频率之和为1,得第二小组的频率等于1-0.7=0.3,则根据频率=频数÷总数,可得第二小组的频数是50×0.3=15.
故选:C.
10.D
【解析】∵硬币只有正反两面,
∴投掷时正面朝上的概率为,
根据频率的概念可知投掷次数逐渐增加,P稳定在附近,
故选D.
11.C
【解析】频率的平均数为:(0.582+0.64+0.5805+0.5908+0.6053+0.601)÷6≈0.6,
50×0.6=30,
故选C.
12.A
【解析】根据频数分布直方图的特点,以及中位数的定义,可知:
(1)从频率分布直方图上看成绩在49.5分~59.5分段的人数与89.5分~100分段的人数相等,故正确;
(2)从频率分布直方图上看出:成绩在79.5~89.5分段的人数占30%,故正确;
(3)成绩在79.5分以上的学生有50×(30%+10%)=20人,故正确;
(4)将该组数据按从大到小的顺序排列,本次考试成绩的中位数落在69.5~79.5分段内,故正确.
故选:A.
13.8
【解析】试题解析:应分(70-42)÷4=7,
∵第一组的下限应低于最小变量值,最后一组的上限应高于最大变量值,
∴应分8组.
故答案为:8.
14. 180 55%
【解析】试题解析:第五小组的频率为1 0.1 0.15 0.2 0.3 0.05=0.20;
总女生人数=36÷0.2=180人,
24次以上的频率为0.3+0.2+0.05=0.55,
即达标率为0.55÷1=0.55;
故答案为:
15. 165cm~170cm 18
【解析】试题解析:八年级一班共有48名学生,他们身高的频数分布直方图如图,各小长方形的高的比为1:1:3:2:1,
∴最高的即表示在这个身高范围内的学生最多,
∴165cm 170cm这个身高范围内的学生最多,
这个身高范围内的学生有:人.
故答案为:165cm 170cm,18.
16. 0.4 12
【解析】试题解析:读图可知:各小长方形的高之比AE:BF:CG:DH=2:4:3:1,即各组频数之比2:4:3:1,
则第2组的频数为×30=12,其频率为=0.4.
故本题答案为:0.4;12.
17.160
【解析】如图,低于40km/h的频率为0.05,超过70km/h的车辆的频率为0.11,
又某天,有1000辆汽车经过了该路段,
故违规扣分的车辆大约为1000×(0.05+0.11)=160辆,
故答案为:160.
【点睛】本题考查了用样本的频率分布估计总体分布、频率分布直方图等,解题时要注意直方图中纵轴的单位与横轴的单位.
18.①③④
【解析】试题解析:参赛学生共有 人,所以①正确;根据频数直方图,比赛成绩在60.5-70.5分段的学生有12人,故②错误;因为参赛人数为52人,那么中位数应为第26、27名成绩的平均数,由频数分布图,第26、27名的成绩在70.5-80.5分段内,所以中位数落在70.5-80.5分段,故③正确;比赛成绩在80分以上的人数为16人,则获奖率为 ,故④正确.
所以本题的正确答案为①③④.
19.(1) 100人;(2)人数最多的年龄段是30岁~39岁,人数最少的年龄段是80岁~89岁;(3)频数是16,所占百分比为16%.
【解析】试题分析:(1)将所有年龄段的人数相加求和即可求解;
(2)找出表格人数一栏的最大、最小值,即可求解;
(3)计算出抽样统计中60岁以上(含60岁)的人数,即可求出所占的百分比,
试题解析:(1)共调查:9+11+17+18+17+12+8+6+2=100(人),
因此,这次共抽查了100人;
(2)观察发现30-39岁年龄段人数最多,80-89岁年龄段人数最少;
(3)观察发现60岁以上的频数是8+6+2=16,频率是
20.(1)详见解析;(2)这组数据的中位数落在第3组;(3)24人.
【解析】试题分析:(1)由分组50.5-60.5的频数和频率得到总数,即可得到60.5-70.5的频率,由所有频率之和等于1,得到80.5-90.5的频率,进而得到对应的频数;
(2)由这组数据共有50个,中位数是第25和26两个数的平均数,这两个数都在第三组内
故它们的平均数也在这组内,从而得到结论;
(3)用总人数×优秀人数百分比即可得到结论.
试题解析:解:(1)0.08÷4=0.02 6×0.02=0.12;
4÷0.08=50 50-(4+6+16+8)=16 16×0.02=0.32;
补全频数分布表和频数分布直方图;
分组 频数 频率
50.5-60.5 4 0.08
60.5-70.5 6 0.12
70.5-80.5 16 0.32
80.5-90.5 16 0.32
90.5-100.5 8 0.16
合计 50 1.00
(2)∵这组数据共有50个,中位数是第25和26两个数的平均数,这两个数都在第三组内
∴它们的平均数也在这组内,∴这组数据的中位数落在第3组;
(3)∵90分以上成绩为优秀,优秀人数百分比是8÷50=16%
∴ 16%×400=24(人);
答:若90分以上成绩为优秀,估计我区获得优秀学生约有24人.
21.(1)50(2)见解析(3)见解析(4)246
【解析】试题分析:(1)根据统计图可知0~0.5小时的人数和百分比,用除法可求解;
(2)根据总人数和已知各时间段的人数,求出九年级(1)班学生每天阅读时间在0.5~1 h的人数,画图即可;
(3)根据除九年级(1)班外,九年级其他班级每天阅读时间为1~1.5 h的学生有165人,除以总人数得到百分比,即可画扇形图;
(4)根据扇形统计图求出其它班符合条件的人数,再加上九年级(1)班符合条件的人数即可.
试题解析:(1)4÷8%=50
(2)九年级(1)班学生每天阅读时间在0.5~1 h的有
50-4-18-8=20(人),
补全频数分布直方图如图所示.
(3)因为除九年级(1)班外,九年级其他班级每天阅读时间在1~1.5 h的学生有165人,
所以1~1.5 h在扇形统计图中所占的百分比为165÷(600-50)×100%=30%,
故0.5~1 h在扇形统计图中所占的百分比为1-30%-10%-12%=48%,
补全扇形统计图如图所示.
(4)该年级每天阅读时间不少于1 h的学生有(600-50)×(30%+10%)+18+8=246(人).
22.(1)见解析(2) 279
【解析】试题分析:(1)由已知信息,根据频数、频率和总量的关系,求出月均用水量4≤x<5所占百分比和频数,月均用水量6≤x<7的频数,从而补全频数分布表和频数分布直方图.
(2)求出样本中家庭月均用水量“大于或等于4t且小于7t” 所占百分比,即可用样本估计总体.
试题解析:(1)调查的总数是50户,
则6≤x<7的户数是50×12%=6(户),
则4≤x<5的户数是50-2-12-10-6-3-2=15(户),
所占的百分比是×100%=30%.
补全频数分布表如下:
月均用水量/t 频数 百分比
2≤x<3 2 4%
3≤x<4 12 24%
4≤x<5 15 30%
5≤x<6 10 20%
6≤x<7 6 12%
7≤x<8 3 6%
8≤x<9 2 4%
补全频数分布直方图如图.
(2)中等用水量家庭大约有450×(30%+20%+12%)=279(户).
23. (1)抽取的200名学生的汉字听写成绩,200,80,0.12.(2)(3)见试题解析
【解析】试题分析:(1)根据第一组的频数是16,频率是0.08,即可求得总数,即样本容量;
(2)根据(1)的计算结果即可作出直方图;
(3)利用总数1000乘以优秀的所占的频率即可.
试题解析:(1) 本次抽样调查的样本是抽取的200名学生的汉字听写成绩,
样本容量是:16÷0.08=200;
m=200×0.40=80,
故答案为:抽取的200名学生的汉字听写成绩,200,80,0.12.
(2)补全频数分布直方图,如下:
(3) ∵样本中成绩在80.5~90.5内的频率是0.4,成绩在90.5~100.5内的频率是0.12,
∴该校八年级学生中汉字听写能力优秀的人数为:1000 (0.4+0.12)=520(人).
答:该校八年级学生中汉字听写能力优秀的约有520人.
24.答案见解析
【解析】试题分析:(1)根据题意制作频数分布表即可;
(2)根据题意绘制频数直方图即可;
(3)根据题意即可得到结论.
试题解析:
(1)将样本数据适当分组,制作频数分布表:
分 组 [50,59] [60,69] [70,79] [80,89] [90,100]
频 数 5 10 15 6 4
故答案为:[50,59],[60,69],[70,79],[80,89],[90,100],5,10,15,6,4;
(2)根据频数分布表,绘制频数直方图:
(3)从图可以看出,这40名学生的成绩都分布在50∽100分范围内,分数在70﹣80之间的人数最多.
25.(1)B,C;(2)2;(3)332.
【解析】试题分析:(1)根据众数的定义,以及中位数的定义解答即可;
(2)先求出女生身高在E组所占的百分比,再求出总人数然后计算即可得解;
(3)分别用男、女生的人数乘以C、D两组的频率的和,计算即可得解.
试题解析:
∵B组人数最多,
∴众数在B组,
男生总人数为4+12+10+8+6=40,
按照从低到高的顺序,第20、21两人都在C组,
∴中位数在C组,
故答案为:B、C;
(2)女生身高在E组的频率为:1-17.5%-37.5%-25%-15%=5%,
∵抽取的样本中,男生、女生的人数相同,
∴样本中,女生身高在E组的人数有40×5%=2人,
故答案为:2;
(3)400× +380×(25%+15%)=180+152=332(人).
答:估计该校身高在160≤x<170之间的学生约有332人.
【点睛】读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
26.(1)50;(2)10;(3)5
【解析】试题分析:(1)直接根据条形统计图获得数据;
(2)根据丙组的25人占总体的50%,即可计算总体人数,然后计算乙组的人数,补全统计图;
(3)设需从甲组抽调x名同学到丙组,根据丙组人数是甲组人数的3倍列方程求解.
试题解析:(1)参加丙组的人数为25人;
(2)25÷50%=50人,则乙组人数=50-25-15=10人,
如图:
(3)设需从甲组抽调x名同学到丙组,
根据题意得:3(15-x)=25+x
解得x=5.
答:应从甲抽调5名学生到丙组.
点睛:读懂统计图,能够从统计图中获得正确信息.第(3)小题中,注意调人的时候,甲组少了x人,则丙组多了x人.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
第5章 数据的频数分布单元检测卷
班级__________姓名____________总分___________
一、选择题
1.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其他完全相同小张通过多次摸球试验后发现,其中摸到红色、黑色球的频率稳定在和,则口袋中白色球的个数很可能是( )
A. 6 B. 16 C. 18 D. 24
2.在频数分布直方图中,各小长方形的高等于相应组的( )
A. 组距 B. 组数 C. 频数 D. 频率
3.袋子里有4个黑球,m个白球,它们除颜色外都相同,经过大量实验,从中任取一个球恰好是白球的频率是0.20,则m的值是( )
A. 1 B. 2 C. 4 D. 16
4.某校对 EMBED Equation.DSMT4 名女生的身高进行了测量,身高在 (单位: )这一小组的频率为 ,则该组的人数为 ( )
A. 人 B. 人 C. 人 D. 人
5.调查某班 EMBED Equation.DSMT4 名同学的跳高成绩时,在收集到的数据中,不足 米的数出现的频率是 ,则达到或超过 米的数出现的频率是 ( )
A. B. C. D.
6.一个容量为 EMBED Equation.DSMT4 的样本最大值为 ,最小值 ,取组距为 ,则可以分成 ( )
A. 组 B. 组 C. 组 D. 组
7.在统计中频率分布的主要作用是( )
A. 可以反映一组数据的波动大小 B. 可以反映一组数据的平均水平
C. 可以反映一组数据的分布情况 D. 可以看出一组数据的最大值和最小值
8.为了筹备班级联欢会,班长对全班50名同学喜欢吃哪几种水果作了民意调查,小明将班长的统计结果绘成如图的统计图,并得出四个结论,其中错误的是( )
A. 一个人可以喜欢吃几种水果
B. 喜欢吃葡萄的人最多
C. 喜欢吃苹果的人数是喜欢吃梨的人数的3倍
D. 喜欢吃香蕉的人数占全班人数的20%
9.将50个数据分成3组,其中第一组和第三组的频率之和为0.7,则第二小组的频数是( )
A. 0.3 B. 30 C. 15 D. 35
10.投掷硬币m次,正面向上n次,其频率p= EMBED Equation.DSMT4 ,则下列说法正确的是( )
A. p一定等于 B. p一定不等于
C. 多投一次,p更接近 D. 投掷次数逐步增加,p稳定在附近
11.在一个不透明的口袋里装着只有颜色不同的黑、白两种颜色的球共50只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复以上步骤,下表为实验的一组统计数据:
摸球的次数n 1000 1500 2000 5000 8000 10000
摸到白球的次数m 582 960 1161 2954 4842 6010
摸到白球的频率 0.582 0.64 0.5805 0.5908 0.6053 0.601
请估算口袋中白球的个数约为( )
A. 20 B. 25 C. 30 D. 35
12.某班50名学生期末考试数学成绩(单位:分)的频率分布直方图如图所示,其中数据不在分点上,对图中提供的信息作出如下的判断:
(1)成绩在49.5分~59.5分段的人数与89.5分~100分段的人数相等;
(2)成绩在79.5~89.5分段的人数占30%;
(3)成绩在79.5分以上的学生有20人;
(4)本次考试成绩的中位数落在69.5~79.5分段内.
其中正确的判断有( )
A. 4个 B. 3个 C. 2个 D. 1个
二、填空题
13.小强调查“每人每天的用水量”这一问题时,收集到80个数据,最大数据是70升,最小数据是42升,若取组距为4,则应分为_________组绘制频数分布表.
14.某中学对七年级女生仰卧起坐的测试成绩进行统计分析,将数据整理后,画出频数分布直方图(如图).已知图中从左到右的第一、第二、第三、第四、第六小组的百分比依次是10%,15%,20%,30%,5%,第五小组的频数是36,则参加这次测试的女生人数是____;若次数在24次(含24次)以上为达标,则该校七年级女生的达标率为______.
15.七年级一班共有48名学生,他们身高的频数分布直方图如图,各小长方形的高的比为1∶1∶3∶2∶1,则身高范围在__________________的学生最多,是____人.
16.已知样本容量为30,在以下样本频率分布直方图中,各小长方形的高之比AE∶BF∶CG∶DH=2∶4∶3∶1,则第2组的频率和频数分别为_______、_______.
17.某市内有一条主干路段,为了使行车安全同时也能增加车流量,规定通过该路段的汽车时速不得低于40km/h,也不得超过70km/h,否则视为违规扣分.某天有1000辆汽车经过了该路段,经过雷达测速得到这些汽车行驶时速的频率分布直方图如图所示,则违规扣分的汽车大约为________辆.
18.某校举办以“保护环境,治理雾霾,从我做起”为主题的演讲比赛,现将所有比赛成绩(得分取整数,满分为100分)进行整理后分为5组,并绘制成如图所示的频数直方图.根据频数分布直方图提供的信息,下列结论:①参加比赛的学生共有52人;②比赛成绩为65分的学生有12人;③比赛成绩的中位数落在70.5~80.5分这个分数段;④如果比赛成绩在80分以上(不含80分)可以获得奖励,则本次比赛的获奖率约为30.8%.正确的是________.(把所有正确结论的序号都填在横线上)
三、解答题
19.在对某地区的一次人口抽样统计分析中,各年龄段(年龄为整数)的人数如下表所示.请根据此表回答下列问题:
年龄段 0~9 10~19 20~29 30~39 40~49 50~59 60~69 70~79 80~89
人数 9 11 17 18 17 12 8 6 2
(1)这次共调查了多少人?
(2)哪个年龄段的人数最多?哪个年龄段的人数最少?
(3)年龄在60岁以上(含60岁)的频数是多少?所占百分比是多少?
20.为了参加市举办“科学发现杯”知识竞赛活动,我区开展了预赛,400名学生参加此次比赛,为了解此次竞赛情况:
从中抽取一部分学生成绩统计如下(得分取整数,满分为100分)
(1)补全频数分布表和频数分布直方图.
(2)这组数据的中位数落在第几组?
(3)若90分以上成绩为优秀,估计我区获得优秀学生约有多少?
分组 频数 频率
50.5-60.5 4 0.08
60.5-70.5 6
70.5-80.5 16 0.32
80.5-90.5
90.5-100.5 8 0.16
合计 1.00
21.4月23日是“世界读书日”,学校开展“让书香溢满校园”读书活动,以提升青少年的阅读兴趣,九年级(1)班数学活动小组对本年级600名学生每天阅读时间进行了统计,根据所得数据绘制了如图所示的两幅不完整的统计图(每组包括最小值不包括最大值)九年级(1)班每天阅读时间在0.5 h以内的学生占全班人数的8%,根据统计图解答下列问题:
(1)九年级(1)班有________名学生.
(2)补全频数分布直方图.
(3)除九年级(1)班外,九年级其他班级每天阅读时间为1~1.5 h的学生有165人,请你补全扇形统计图.
(4)求该年级每天阅读时间不少于1 h的学生有多少人.
22.小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况,他从中随机调查了50户居民的月均用水量(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1)请根据题中已有的信息补全频数分布表和频数分布直方图;
月均用水量/t 频数 百分比
2≤x<3 2 4%
3≤x<4 12 24%
4≤x<5
5≤x<6 10 20%
6≤x<7 12%
7≤x<8 3 6%
8≤x<9 2 4%
(2)如果家庭月均用水量“大于或等于4 t且小于7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.
23.为弘扬中华传统文化,某校组织八年级1000名学生参加汉字听写大赛,为了解学生整体听写能力,从中抽取部分学生的成绩(得分取正整数,满分为100分)进行统计分析,请根据尚未完成的下列图表,解答问题:
组别 分数段 频数 频率
一 50.5~60.5 16 0.08
二 60.5~70.5 30 0.15
三 70.5~80.5 50 0.25
四 80.5~90.5 m 0.40
五 90.5~100.5 n
(1)本次抽样调查的样本是__________________,样本容量为________,表中m=________,n=________;
(2)补全频数分布直方图;
(3)若抽取的样本具有较好的代表性,且成绩超过80分为优秀,根据样本估计该校八年级学生中汉字听写能力优秀的约有多少人?
24.为了解上一次八年级数学测验成绩情况,随机抽取了40名学生的成绩进行统计分析,这40名学生的成绩数据如下:
55 62 67 53 58 83 87 64 68 85
60 94 81 98 51 83 78 77 66 71
91 72 63 75 88 73 52 71 79 63
74 67 78 61 97 76 72 77 79 71
(1)将样本数据适当分组,制作频数分布表:
分 组
频 数
(2)根据频数分布表,绘制频数直方图:
(3)从图可以看出,这40名学生的成绩都分布在什么范围内?分数在哪个范围的人数最多?
25.为了解某校学生的身高情况,随机抽取该校若干男生、女生进行抽样调查.已知抽取的样本中,男生、女生人数相同,利用所得数据绘制如下统计表和统计图(如图20-3-2所示):
身高情况分组表(单位:cm)
组别 身高
A x<155
B 155≤x<160
C 160≤x<165
D 165≤x<170
E x≥170
根据图表提供的信息,回答下列问题:
(1)样本中,男生身高的众数在___________组,中位数在___________组;
(2)样本中,女生身高在E组的有___________人;
(3)已知该校共有男生400人、女生380人,请估计身高在160≤x<170范围内的学生约有多少人.
26.某年级组织学生参加夏令营,分为甲、乙、丙三组进行活动.下面两幅统计图反映了学生报名参加夏令营的情况.请你根据图中的信息回答下列问题:
报名人数分布直方图 报名人数扇形统计图
(1)求该年级报名参加本次活动的总人数;
(2)求该年级报名参加乙组的人数,并补全频数分布直方图;
(3)根据实际情况,需从甲组抽调部分同学到丙组,使丙组人数是甲组人数的3倍,那么,应从甲组抽调多少名学生到丙组?
参考答案
1.B
【解析】试题解析: 根据红色、黑色球的频率稳定在15%和45%,那么白色玻璃球出现的频率为1-15%-45%=40%,
根据多次实验中,可用一个事件发生的频率作为这个事件的概率的估计值,那么袋中有白色球的概率为
故口袋中白色球的个数为
故选B.
2.C
【解析】试题解析:在频数分布直方图中,每个小长方形的高等于每小组的频数.
故选C.
3.A
【解析】试题解析:袋子里有4个黑球,m个白球,若从中任取一个球恰好是白球的概率是
根据题意可得:
解得m=1.
故选A.
4.B
【解析】试题解析:根据题意,得
该组的人数为1200×0.25=300(人).
故选B.
5.B
【解析】试题解析:在收集到的数据中,不足 米的数出现的频率是 ,
则达到或超过 米的数出现的频率是:
故选B.
6.B
【解析】试题解析:最大值与最小值的差为:
因为
所以分成9组较为恰当.
故选B.
7.C
【解析】由平均数、方差的概念,可知它们分别反映总体的平均水平和波动大小,故A、B不正确;
根据统计中,频率是指每个对象出现的次数与总次数的比值(或百分比),频率反映了个组频数的大小在总数中所占的分量,即可以反映总体的分布情况.
故选:C.
点睛:本题考查了频率的意义,一般称落在不同小组中的数据个数为该组的频数,频数与数据总数的比值为频率.
8.D
【解析】30+10+20+40=100>50,所以一个人可以喜欢吃几种水果,故A选项正确;
喜欢吃葡萄的最多,为40人,故B选项正确;
喜欢吃苹果的有30人,喜欢吃梨的有10人,喜欢吃苹果的人数是喜欢吃梨的人数的3倍,故C选项正确;
喜欢吃香蕉的有20人,占全班总人数的:20÷50=40%,故D选项错误.
故选D.
点睛:掌握条形统计图.
9.C
【解析】根据频率的性质,各组的频率之和为1,得第二小组的频率等于1-0.7=0.3,则根据频率=频数÷总数,可得第二小组的频数是50×0.3=15.
故选:C.
10.D
【解析】∵硬币只有正反两面,
∴投掷时正面朝上的概率为,
根据频率的概念可知投掷次数逐渐增加,P稳定在附近,
故选D.
11.C
【解析】频率的平均数为:(0.582+0.64+0.5805+0.5908+0.6053+0.601)÷6≈0.6,
50×0.6=30,
故选C.
12.A
【解析】根据频数分布直方图的特点,以及中位数的定义,可知:
(1)从频率分布直方图上看成绩在49.5分~59.5分段的人数与89.5分~100分段的人数相等,故正确;
(2)从频率分布直方图上看出:成绩在79.5~89.5分段的人数占30%,故正确;
(3)成绩在79.5分以上的学生有50×(30%+10%)=20人,故正确;
(4)将该组数据按从大到小的顺序排列,本次考试成绩的中位数落在69.5~79.5分段内,故正确.
故选:A.
13.8
【解析】试题解析:应分(70-42)÷4=7,
∵第一组的下限应低于最小变量值,最后一组的上限应高于最大变量值,
∴应分8组.
故答案为:8.
14. 180 55%
【解析】试题解析:第五小组的频率为1 0.1 0.15 0.2 0.3 0.05=0.20;
总女生人数=36÷0.2=180人,
24次以上的频率为0.3+0.2+0.05=0.55,
即达标率为0.55÷1=0.55;
故答案为:
15. 165cm~170cm 18
【解析】试题解析:八年级一班共有48名学生,他们身高的频数分布直方图如图,各小长方形的高的比为1:1:3:2:1,
∴最高的即表示在这个身高范围内的学生最多,
∴165cm 170cm这个身高范围内的学生最多,
这个身高范围内的学生有:人.
故答案为:165cm 170cm,18.
16. 0.4 12
【解析】试题解析:读图可知:各小长方形的高之比AE:BF:CG:DH=2:4:3:1,即各组频数之比2:4:3:1,
则第2组的频数为×30=12,其频率为=0.4.
故本题答案为:0.4;12.
17.160
【解析】如图,低于40km/h的频率为0.05,超过70km/h的车辆的频率为0.11,
又某天,有1000辆汽车经过了该路段,
故违规扣分的车辆大约为1000×(0.05+0.11)=160辆,
故答案为:160.
【点睛】本题考查了用样本的频率分布估计总体分布、频率分布直方图等,解题时要注意直方图中纵轴的单位与横轴的单位.
18.①③④
【解析】试题解析:参赛学生共有 人,所以①正确;根据频数直方图,比赛成绩在60.5-70.5分段的学生有12人,故②错误;因为参赛人数为52人,那么中位数应为第26、27名成绩的平均数,由频数分布图,第26、27名的成绩在70.5-80.5分段内,所以中位数落在70.5-80.5分段,故③正确;比赛成绩在80分以上的人数为16人,则获奖率为 ,故④正确.
所以本题的正确答案为①③④.
19.(1) 100人;(2)人数最多的年龄段是30岁~39岁,人数最少的年龄段是80岁~89岁;(3)频数是16,所占百分比为16%.
【解析】试题分析:(1)将所有年龄段的人数相加求和即可求解;
(2)找出表格人数一栏的最大、最小值,即可求解;
(3)计算出抽样统计中60岁以上(含60岁)的人数,即可求出所占的百分比,
试题解析:(1)共调查:9+11+17+18+17+12+8+6+2=100(人),
因此,这次共抽查了100人;
(2)观察发现30-39岁年龄段人数最多,80-89岁年龄段人数最少;
(3)观察发现60岁以上的频数是8+6+2=16,频率是
20.(1)详见解析;(2)这组数据的中位数落在第3组;(3)24人.
【解析】试题分析:(1)由分组50.5-60.5的频数和频率得到总数,即可得到60.5-70.5的频率,由所有频率之和等于1,得到80.5-90.5的频率,进而得到对应的频数;
(2)由这组数据共有50个,中位数是第25和26两个数的平均数,这两个数都在第三组内
故它们的平均数也在这组内,从而得到结论;
(3)用总人数×优秀人数百分比即可得到结论.
试题解析:解:(1)0.08÷4=0.02 6×0.02=0.12;
4÷0.08=50 50-(4+6+16+8)=16 16×0.02=0.32;
补全频数分布表和频数分布直方图;
分组 频数 频率
50.5-60.5 4 0.08
60.5-70.5 6 0.12
70.5-80.5 16 0.32
80.5-90.5 16 0.32
90.5-100.5 8 0.16
合计 50 1.00
(2)∵这组数据共有50个,中位数是第25和26两个数的平均数,这两个数都在第三组内
∴它们的平均数也在这组内,∴这组数据的中位数落在第3组;
(3)∵90分以上成绩为优秀,优秀人数百分比是8÷50=16%
∴ 16%×400=24(人);
答:若90分以上成绩为优秀,估计我区获得优秀学生约有24人.
21.(1)50(2)见解析(3)见解析(4)246
【解析】试题分析:(1)根据统计图可知0~0.5小时的人数和百分比,用除法可求解;
(2)根据总人数和已知各时间段的人数,求出九年级(1)班学生每天阅读时间在0.5~1 h的人数,画图即可;
(3)根据除九年级(1)班外,九年级其他班级每天阅读时间为1~1.5 h的学生有165人,除以总人数得到百分比,即可画扇形图;
(4)根据扇形统计图求出其它班符合条件的人数,再加上九年级(1)班符合条件的人数即可.
试题解析:(1)4÷8%=50
(2)九年级(1)班学生每天阅读时间在0.5~1 h的有
50-4-18-8=20(人),
补全频数分布直方图如图所示.
(3)因为除九年级(1)班外,九年级其他班级每天阅读时间在1~1.5 h的学生有165人,
所以1~1.5 h在扇形统计图中所占的百分比为165÷(600-50)×100%=30%,
故0.5~1 h在扇形统计图中所占的百分比为1-30%-10%-12%=48%,
补全扇形统计图如图所示.
(4)该年级每天阅读时间不少于1 h的学生有(600-50)×(30%+10%)+18+8=246(人).
22.(1)见解析(2) 279
【解析】试题分析:(1)由已知信息,根据频数、频率和总量的关系,求出月均用水量4≤x<5所占百分比和频数,月均用水量6≤x<7的频数,从而补全频数分布表和频数分布直方图.
(2)求出样本中家庭月均用水量“大于或等于4t且小于7t” 所占百分比,即可用样本估计总体.
试题解析:(1)调查的总数是50户,
则6≤x<7的户数是50×12%=6(户),
则4≤x<5的户数是50-2-12-10-6-3-2=15(户),
所占的百分比是×100%=30%.
补全频数分布表如下:
月均用水量/t 频数 百分比
2≤x<3 2 4%
3≤x<4 12 24%
4≤x<5 15 30%
5≤x<6 10 20%
6≤x<7 6 12%
7≤x<8 3 6%
8≤x<9 2 4%
补全频数分布直方图如图.
(2)中等用水量家庭大约有450×(30%+20%+12%)=279(户).
23. (1)抽取的200名学生的汉字听写成绩,200,80,0.12.(2)(3)见试题解析
【解析】试题分析:(1)根据第一组的频数是16,频率是0.08,即可求得总数,即样本容量;
(2)根据(1)的计算结果即可作出直方图;
(3)利用总数1000乘以优秀的所占的频率即可.
试题解析:(1) 本次抽样调查的样本是抽取的200名学生的汉字听写成绩,
样本容量是:16÷0.08=200;
m=200×0.40=80,
故答案为:抽取的200名学生的汉字听写成绩,200,80,0.12.
(2)补全频数分布直方图,如下:
(3) ∵样本中成绩在80.5~90.5内的频率是0.4,成绩在90.5~100.5内的频率是0.12,
∴该校八年级学生中汉字听写能力优秀的人数为:1000 (0.4+0.12)=520(人).
答:该校八年级学生中汉字听写能力优秀的约有520人.
24.答案见解析
【解析】试题分析:(1)根据题意制作频数分布表即可;
(2)根据题意绘制频数直方图即可;
(3)根据题意即可得到结论.
试题解析:
(1)将样本数据适当分组,制作频数分布表:
分 组 [50,59] [60,69] [70,79] [80,89] [90,100]
频 数 5 10 15 6 4
故答案为:[50,59],[60,69],[70,79],[80,89],[90,100],5,10,15,6,4;
(2)根据频数分布表,绘制频数直方图:
(3)从图可以看出,这40名学生的成绩都分布在50∽100分范围内,分数在70﹣80之间的人数最多.
25.(1)B,C;(2)2;(3)332.
【解析】试题分析:(1)根据众数的定义,以及中位数的定义解答即可;
(2)先求出女生身高在E组所占的百分比,再求出总人数然后计算即可得解;
(3)分别用男、女生的人数乘以C、D两组的频率的和,计算即可得解.
试题解析:
∵B组人数最多,
∴众数在B组,
男生总人数为4+12+10+8+6=40,
按照从低到高的顺序,第20、21两人都在C组,
∴中位数在C组,
故答案为:B、C;
(2)女生身高在E组的频率为:1-17.5%-37.5%-25%-15%=5%,
∵抽取的样本中,男生、女生的人数相同,
∴样本中,女生身高在E组的人数有40×5%=2人,
故答案为:2;
(3)400× +380×(25%+15%)=180+152=332(人).
答:估计该校身高在160≤x<170之间的学生约有332人.
【点睛】读频数分布直方图的能力和利用统计图获取信息的能力;利用统计图获取信息时,必须认真观察、分析、研究统计图,才能作出正确的判断和解决问题.
26.(1)50;(2)10;(3)5
【解析】试题分析:(1)直接根据条形统计图获得数据;
(2)根据丙组的25人占总体的50%,即可计算总体人数,然后计算乙组的人数,补全统计图;
(3)设需从甲组抽调x名同学到丙组,根据丙组人数是甲组人数的3倍列方程求解.
试题解析:(1)参加丙组的人数为25人;
(2)25÷50%=50人,则乙组人数=50-25-15=10人,
如图:
(3)设需从甲组抽调x名同学到丙组,
根据题意得:3(15-x)=25+x
解得x=5.
答:应从甲抽调5名学生到丙组.
点睛:读懂统计图,能够从统计图中获得正确信息.第(3)小题中,注意调人的时候,甲组少了x人,则丙组多了x人.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
