2018版题型突破高考数学(文)解答题揭秘专题3.3+压轴大题突破练03(解析几何+函数与导数)(第02期)
文档属性
| 名称 | 2018版题型突破高考数学(文)解答题揭秘专题3.3+压轴大题突破练03(解析几何+函数与导数)(第02期) |  | |
| 格式 | zip | ||
| 文件大小 | 433.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-12 11:22:03 | ||
图片预览

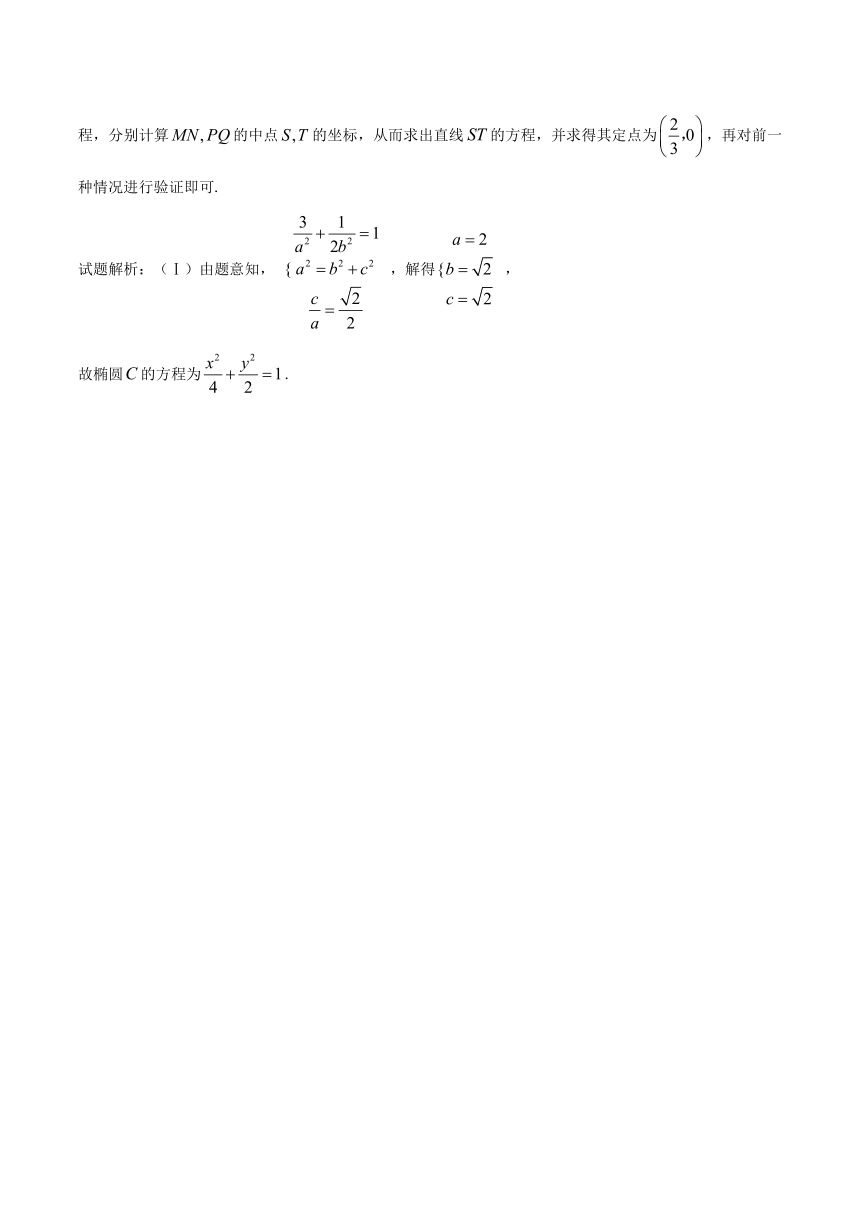
文档简介
类型
试 题 亮 点
解题方法/思想/素养
解析大题
向量与解析几何的综合问题
椭圆中的直线过定点问题
向量问题坐标化的思想
直线过定点的常用方法:
一、设出直线的一般形式,根据题中条件建立方程,从而得定点;
二、通过计算直线上两点坐标得直线方程,从而得定点
导数大题
不等式恒成立问题求参,导函数的零点不可求
设而不求的思想,等量代换,化简函数最值,由零点的额范围恰整数解
1.解析大题
已知椭圆: 的离心率为,且椭圆过点.过点做两条相互垂直的直线、分别与椭圆交于、、、四点.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)若, ,探究:直线是否过定点?若是,请求出定点坐标;若不是,请说明理由.
【答案】(1)(2)
先对后一种情况探究,则可设两直线的方程分别为, ,逐个联立椭圆方程,分别计算的中点的坐标,从而求出直线的方程,并求得其定点为,再对前一种情况进行验证即可.
试题解析:(Ⅰ)由题意知, ,解得,
故椭圆的方程为.
2.导数大题
已知函数在点处的切线过点.
(1)求实数的值,并求出函数单调区间;
(2)若整数使得在上恒成立,求的最大值.
【答案】(1),在单调递减,在单调递增;(2)7.
(2)∵时, ,∴等价于
记 ,∴
记,有 ,∴在单调递增
∴ ,由于,,可得
因此,故
又
由零点存在定理可知,存在,使得,即①
同课章节目录
