传送带问题[下学期]
图片预览
文档简介
物理高考测试题1
传送带问题
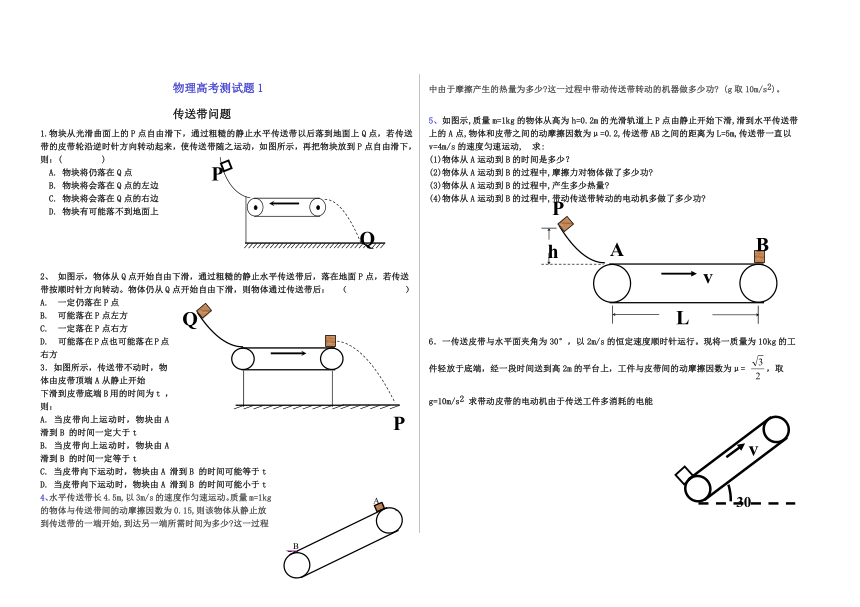
1.物块从光滑曲面上的P点自由滑下,通过粗糙的静止水平传送带以后落到地面上Q点,若传送带的皮带轮沿逆时针方向转动起来,使传送带随之运动,如图所示,再把物块放到P点自由滑下,则:( )
A. 物块将仍落在Q点
B. 物块将会落在Q点的左边
C. 物块将会落在Q点的右边
D. 物块有可能落不到地面上
2、 如图示,物体从Q点开始自由下滑,通过粗糙的静止水平传送带后,落在地面P点,若传送带按顺时针方向转动。物体仍从Q点开始自由下滑,则物体通过传送带后: ( )
A. 一定仍落在P点
B. 可能落在P点左方
C. 一定落在P点右方
D. 可能落在P点也可能落在P点右方
3.如图所示,传送带不动时,物体由皮带顶端A从静止开始
下滑到皮带底端B用的时间为t ,则:
A. 当皮带向上运动时,物块由A 滑到B 的时间一定大于t
B. 当皮带向上运动时,物块由A 滑到B 的时间一定等于t
C. 当皮带向下运动时,物块由A 滑到B 的时间可能等于t
D. 当皮带向下运动时,物块由A 滑到B 的时间可能小于t
4、水平传送带长4.5m,以3m/s的速度作匀速运动。质量m=1kg的物体与传送带间的动摩擦因数为0.15,则该物体从静止放到传送带的一端开始,到达另一端所需时间为多少 这一过程中由于摩擦产生的热量为多少 这一过程中带动传送带转动的机器做多少功 (g取10m/s2)。
5、如图示,质量m=1kg的物体从高为h=0.2m的光滑轨道上P点由静止开始下滑,滑到水平传送带上的A点,物体和皮带之间的动摩擦因数为μ=0.2,传送带AB之间的距离为L=5m,传送带一直以v=4m/s的速度匀速运动, 求:
(1)物体从A运动到B的时间是多少?
(2)物体从A运动到B的过程中,摩擦力对物体做了多少功
(3)物体从A运动到B的过程中,产生多少热量
(4)物体从A运动到B的过程中,带动传送带转动的电动机多做了多少功
6.一传送皮带与水平面夹角为30°,以2m/s的恒定速度顺时针运行。现将一质量为10kg的工件轻放于底端,经一段时间送到高2m的平台上,工件与皮带间的动摩擦因数为μ= ,取g=10m/s2 求带动皮带的电动机由于传送工件多消耗的电能
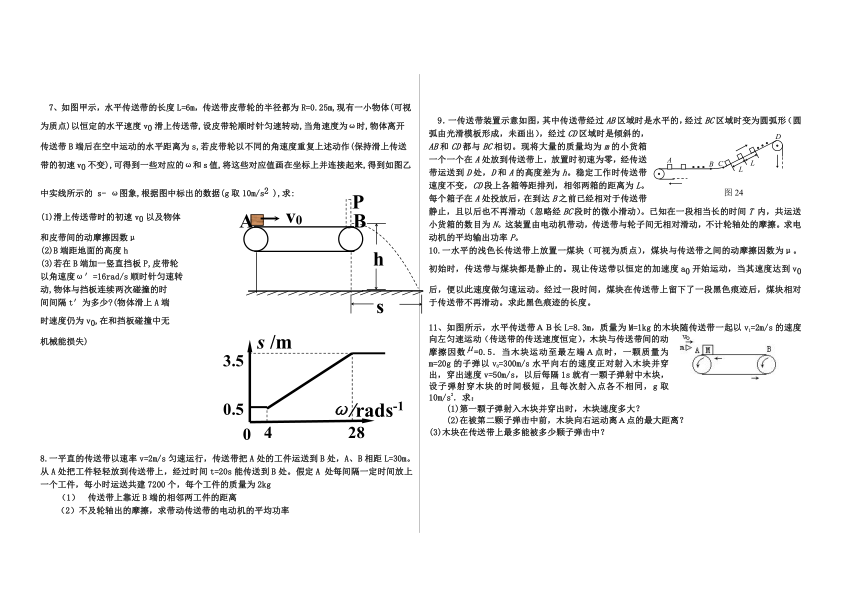
7、如图甲示,水平传送带的长度L=6m,传送带皮带轮的半径都为R=0.25m,现有一小物体(可视为质点)以恒定的水平速度v0滑上传送带,设皮带轮顺时针匀速转动,当角速度为ω时,物体离开传送带B端后在空中运动的水平距离为s,若皮带轮以不同的角速度重复上述动作(保持滑上传送带的初速v0不变),可得到一些对应的ω和s值,将这些对应值画在坐标上并连接起来,得到如图乙中实线所示的 s- ω图象,根据图中标出的数据(g取10m/s2 ),求:
(1)滑上传送带时的初速v0以及物体
和皮带间的动摩擦因数μ
(2)B端距地面的高度h
(3)若在B端加一竖直挡板P,皮带轮
以角速度ω′=16rad/s顺时针匀速转
动,物体与挡板连续两次碰撞的时
间间隔t′为多少 (物体滑上A端
时速度仍为v0,在和挡板碰撞中无
机械能损失)
8.一平直的传送带以速率v=2m/s匀速运行,传送带把A处的工件运送到B处,A、B相距L=30m。从A处把工件轻轻放到传送带上,经过时间t=20s能传送到B处。假定A 处每间隔一定时间放上一个工件,每小时运送共建7200个,每个工件的质量为2kg
传送带上靠近B端的相邻两工件的距离
(2)不及轮轴出的摩擦,求带动传送带的电动机的平均功率
9.一传送带装置示意如图,其中传送带经过AB区域时是水平的,经过BC区域时变为圆弧形(圆弧由光滑模板形成,未画出),经过CD区域时是倾斜的,AB和CD都与BC相切。现将大量的质量均为m的小货箱一个一个在A处放到传送带上,放置时初速为零,经传送带运送到D处,D和A的高度差为h。稳定工作时传送带速度不变,CD段上各箱等距排列,相邻两箱的距离为L。每个箱子在A处投放后,在到达B之前已经相对于传送带静止,且以后也不再滑动(忽略经BC段时的微小滑动)。已知在一段相当长的时间T 内,共运送小货箱的数目为N。这装置由电动机带动,传送带与轮子间无相对滑动,不计轮轴处的摩擦。求电动机的平均输出功率P。
10.一水平的浅色长传送带上放置一煤块(可视为质点),煤块与传送带之间的动摩擦因数为μ。初始时,传送带与煤块都是静止的。现让传送带以恒定的加速度a0开始运动,当其速度达到v0后,便以此速度做匀速运动。经过一段时间,煤块在传送带上留下了一段黑色痕迹后,煤块相对于传送带不再滑动。求此黑色痕迹的长度。
11、如图所示,水平传送带AB长L=8.3m,质量为M=1kg的木块随传送带一起以v1=2m/s的速度向左匀速运动(传送带的传送速度恒定),木块与传送带间的动摩擦因数=0.5.当木块运动至最左端A点时,一颗质量为m=20g的子弹以v0=300m/s水平向右的速度正对射入木块并穿出,穿出速度v=50m/s,以后每隔1s就有一颗子弹射中木块,设子弹射穿木块的时间极短,且每次射入点各不相同,g取10m/s2.求:
(1)第一颗子弹射入木块并穿出时,木块速度多大?
(2)在被第二颗子弹击中前,木块向右运动离A点的最大距离?
(3)木块在传送带上最多能被多少颗子弹击中?
传送带问题参考答案
1.A 2. D 3.BCD
4.解:物体在摩擦力作用下先匀加速运动, 后做匀速运动,
a =μg=1.5m/s2
t1= v / a=2s
S1= 1/2 at12= 3 m
t2=(L-S1)/v=0.5 s
∴t = t1 +t2=2.5 s
木块与传送带的相对位移 ΔS =vt1- S1=3m
Q= μmg ΔS =4.5J
机器做功W= 1/2 mv2 +Q=9J
或W= μmg S皮带= μmg vt1=9J
5.解:(1)物体下滑到A点的速度为v0 ,由机械能守恒定律
1/2 mv02 =mgh v0 =2m/s
物体在摩擦力作用下先匀加速运动, 后做匀速运动,
t1= (v-v0) / μg=1s
S1= (v2-v02 ) / 2μg=3m
t2=(L-S1)/v=0.5s
∴t = t1 +t2=1.5s(2)
Wf=μmg S1= 0.2×10 ×3=6 J 或 Wf= 1/2 mv2 - 1/2 mv02 = 1/2 ×(16-4)= 6 J (3)在t1时间内,皮带做匀速运动 S皮带=v t1 =4m
Q= μmg ΔS = μmg(S皮带- S1)=2J
(4)由能量守恒, W=Q+Wf=8J
或W=μmg S皮带=8J
7.由图象可知:当ω≤ω1=4rad/s时,物体在传送带上一直减速,经过B点时的速度为当ω≥ ω2=28rad/s时,物体在传送带上一直加速,
经过B点时的速度为
由 a=μg, v02 - v12 =2μgL v22 – v02 =2μgL
解得μ=0.2 v0=5m/s
(2)由图象可知:当水平速度为1m/s时,水平距离为0.5m,
t=s/v=0.5s h=1/2 gt2=1.25m
(3) ω′ =16rad/s 物体和板碰撞前后的速度都是v′ =ω′ R =4m/s
第一次碰后速度向左,减速到0, 再向右加速到4m/s时第二次碰板
v0=5m/s v皮=ωR =ω/4 vB=s/t=s/0.5
t' =2 v' /a= 2v'/μg =4s
将s- ω图象转化为vB - v皮图象如图示:
当ω≤4rad/s时, v皮≤1m/s, 物体在传送带上一直减速,
当 4rad/s ≤ω≤20 rad/s时, 1m/s ≤v皮 ≤v0=5m/s,
物体在传送带上先减速,然后以ωR匀速运动
当ω=20rad/s时, v皮=5m/s, 物体在传送带上一直匀速,
当20rad/s ≤ω≤28rad/s时, 5m/s ≤v皮≤7m/s,
物体在传送带上先加速,然后以ωR匀速运动
当ω≥28rad/s时, v皮≥ 7m/s, 物体在传送带上一直加速
9.解析:以地面为参考系(下同),设传送带的运动速度为v0,在水平段运输的过程中,小货箱先在滑动摩擦力作用下做匀加速运动,设这段路程为s,所用时间为t,加速度为a,则对小箱有:
在这段时间内,传送带运动的路程为: S0 =v0 t
由以上可得: S0 =2S
用f 表示小箱与传送带之间的滑动摩擦力,
则传送带对小箱做功为
传送带克服小箱对它的摩擦力做功
A0=f S0=2×1/2·mv02
两者之差就是摩擦力做功发出的热量Q=1/2·mv02
[也可直接根据摩擦生热 Q= f △S= f(S0- S)计算]
可见,在小箱加速运动过程中,小箱获得的动能与发热量相等. Q=1/2·mv02
T时间内,电动机输出的功为:W=PT
此功用于增加小箱的动能、势能以及克服摩擦力发热,即:
W=N· [ 1/2·mv02+mgh+Q ]= N· [ mv02+mgh
已知相邻两小箱的距离为L,所以
v0T=NL v0=NL / T
联立,得:
10.解:根据“传送带上有黑色痕迹”可知,煤块与传送带之间发生了相对滑动,煤块的加速度a小于传送带的加速度a0。根据牛顿定律,可得
a=μg
设经历时间t,传送带由静止开始加速到速度等于v0,煤块则由静止加速到v,有
v0=a0t v=at
由于a此后,煤块与传送带运动速度相同,相对于传送带不再滑动,不再产生新的痕迹。
设在煤块的速度从0增加到v0的整个过程中,传送带和煤块移动的距离分别为s0和s,有
s0=a0t2+v0t' s=
传送带上留下的黑色痕迹的长度 l=s0-s
由以上各式得l=
11. 分析和解答:(1)设子弹第一次射穿木块后的速度为v/(方向向右),则在第一次射穿木块的过程中,对木块和子弹整体由动量守恒定律(取向右方向为正)得:mv0-Mv1=mv+Mv/,可解得v/=3m/s,其方向应向右.
(2)木块向右滑动中加速度大小为a=g=5m/s2,以速度v/=3m/s向右滑行速度减为零时,所用时间为,显然这之前第二颗子弹仍未射出,所以木块向右运动离A点的最大距离.
(3)木块向右运动到离A点的最大距离之后,经0.4s木块向左作匀加速直线运动,并获得速度v//,v//=a0.4=2m/s,即恰好在与皮带速度相等时第二颗子弹将要射入.注意到这一过程中(即第一个1秒内)木块离A点s1= sm-=0.5m.第二次射入一颗子弹使得木块运动的情况与第一次运动的情况完全相同,即在每一秒的时间里,有一颗子弹击中木块,使木块向右运动0.9m,又向左移动s/==0.4m,每一次木块向右离开A点的距离是0.5m.显然,第16颗子弹恰击中木块时,木块离A端的距离是s2=150.5m=7.5m,第16颗子弹击中木块后,木块再向右运动L- s2=8.3m-7.5m=0.8m<0.9m,木块就从右端B滑出.
由此推算,则经过16次子弹射击后木块应将从B点滑出.
P
Q
Q
P
A
B
A
B
B
A
P
v
h
L
30°
v
P
h
v0
s
A
B
ω/rads-1
s /m
0
4
28
0.5
3.5
B
L
L
A
C
D
图24
ω/rads-1
s /m
0
4
28
0.5
3.5
v皮/ms-1
vB /ms-1
0
1
7
1
7
5
5
ω/rads-1
s /m
0
4
28
0.5
3.5
2.5
20
1.5
16
8
1.0
传送带问题
1.物块从光滑曲面上的P点自由滑下,通过粗糙的静止水平传送带以后落到地面上Q点,若传送带的皮带轮沿逆时针方向转动起来,使传送带随之运动,如图所示,再把物块放到P点自由滑下,则:( )
A. 物块将仍落在Q点
B. 物块将会落在Q点的左边
C. 物块将会落在Q点的右边
D. 物块有可能落不到地面上
2、 如图示,物体从Q点开始自由下滑,通过粗糙的静止水平传送带后,落在地面P点,若传送带按顺时针方向转动。物体仍从Q点开始自由下滑,则物体通过传送带后: ( )
A. 一定仍落在P点
B. 可能落在P点左方
C. 一定落在P点右方
D. 可能落在P点也可能落在P点右方
3.如图所示,传送带不动时,物体由皮带顶端A从静止开始
下滑到皮带底端B用的时间为t ,则:
A. 当皮带向上运动时,物块由A 滑到B 的时间一定大于t
B. 当皮带向上运动时,物块由A 滑到B 的时间一定等于t
C. 当皮带向下运动时,物块由A 滑到B 的时间可能等于t
D. 当皮带向下运动时,物块由A 滑到B 的时间可能小于t
4、水平传送带长4.5m,以3m/s的速度作匀速运动。质量m=1kg的物体与传送带间的动摩擦因数为0.15,则该物体从静止放到传送带的一端开始,到达另一端所需时间为多少 这一过程中由于摩擦产生的热量为多少 这一过程中带动传送带转动的机器做多少功 (g取10m/s2)。
5、如图示,质量m=1kg的物体从高为h=0.2m的光滑轨道上P点由静止开始下滑,滑到水平传送带上的A点,物体和皮带之间的动摩擦因数为μ=0.2,传送带AB之间的距离为L=5m,传送带一直以v=4m/s的速度匀速运动, 求:
(1)物体从A运动到B的时间是多少?
(2)物体从A运动到B的过程中,摩擦力对物体做了多少功
(3)物体从A运动到B的过程中,产生多少热量
(4)物体从A运动到B的过程中,带动传送带转动的电动机多做了多少功
6.一传送皮带与水平面夹角为30°,以2m/s的恒定速度顺时针运行。现将一质量为10kg的工件轻放于底端,经一段时间送到高2m的平台上,工件与皮带间的动摩擦因数为μ= ,取g=10m/s2 求带动皮带的电动机由于传送工件多消耗的电能
7、如图甲示,水平传送带的长度L=6m,传送带皮带轮的半径都为R=0.25m,现有一小物体(可视为质点)以恒定的水平速度v0滑上传送带,设皮带轮顺时针匀速转动,当角速度为ω时,物体离开传送带B端后在空中运动的水平距离为s,若皮带轮以不同的角速度重复上述动作(保持滑上传送带的初速v0不变),可得到一些对应的ω和s值,将这些对应值画在坐标上并连接起来,得到如图乙中实线所示的 s- ω图象,根据图中标出的数据(g取10m/s2 ),求:
(1)滑上传送带时的初速v0以及物体
和皮带间的动摩擦因数μ
(2)B端距地面的高度h
(3)若在B端加一竖直挡板P,皮带轮
以角速度ω′=16rad/s顺时针匀速转
动,物体与挡板连续两次碰撞的时
间间隔t′为多少 (物体滑上A端
时速度仍为v0,在和挡板碰撞中无
机械能损失)
8.一平直的传送带以速率v=2m/s匀速运行,传送带把A处的工件运送到B处,A、B相距L=30m。从A处把工件轻轻放到传送带上,经过时间t=20s能传送到B处。假定A 处每间隔一定时间放上一个工件,每小时运送共建7200个,每个工件的质量为2kg
传送带上靠近B端的相邻两工件的距离
(2)不及轮轴出的摩擦,求带动传送带的电动机的平均功率
9.一传送带装置示意如图,其中传送带经过AB区域时是水平的,经过BC区域时变为圆弧形(圆弧由光滑模板形成,未画出),经过CD区域时是倾斜的,AB和CD都与BC相切。现将大量的质量均为m的小货箱一个一个在A处放到传送带上,放置时初速为零,经传送带运送到D处,D和A的高度差为h。稳定工作时传送带速度不变,CD段上各箱等距排列,相邻两箱的距离为L。每个箱子在A处投放后,在到达B之前已经相对于传送带静止,且以后也不再滑动(忽略经BC段时的微小滑动)。已知在一段相当长的时间T 内,共运送小货箱的数目为N。这装置由电动机带动,传送带与轮子间无相对滑动,不计轮轴处的摩擦。求电动机的平均输出功率P。
10.一水平的浅色长传送带上放置一煤块(可视为质点),煤块与传送带之间的动摩擦因数为μ。初始时,传送带与煤块都是静止的。现让传送带以恒定的加速度a0开始运动,当其速度达到v0后,便以此速度做匀速运动。经过一段时间,煤块在传送带上留下了一段黑色痕迹后,煤块相对于传送带不再滑动。求此黑色痕迹的长度。
11、如图所示,水平传送带AB长L=8.3m,质量为M=1kg的木块随传送带一起以v1=2m/s的速度向左匀速运动(传送带的传送速度恒定),木块与传送带间的动摩擦因数=0.5.当木块运动至最左端A点时,一颗质量为m=20g的子弹以v0=300m/s水平向右的速度正对射入木块并穿出,穿出速度v=50m/s,以后每隔1s就有一颗子弹射中木块,设子弹射穿木块的时间极短,且每次射入点各不相同,g取10m/s2.求:
(1)第一颗子弹射入木块并穿出时,木块速度多大?
(2)在被第二颗子弹击中前,木块向右运动离A点的最大距离?
(3)木块在传送带上最多能被多少颗子弹击中?
传送带问题参考答案
1.A 2. D 3.BCD
4.解:物体在摩擦力作用下先匀加速运动, 后做匀速运动,
a =μg=1.5m/s2
t1= v / a=2s
S1= 1/2 at12= 3 m
t2=(L-S1)/v=0.5 s
∴t = t1 +t2=2.5 s
木块与传送带的相对位移 ΔS =vt1- S1=3m
Q= μmg ΔS =4.5J
机器做功W= 1/2 mv2 +Q=9J
或W= μmg S皮带= μmg vt1=9J
5.解:(1)物体下滑到A点的速度为v0 ,由机械能守恒定律
1/2 mv02 =mgh v0 =2m/s
物体在摩擦力作用下先匀加速运动, 后做匀速运动,
t1= (v-v0) / μg=1s
S1= (v2-v02 ) / 2μg=3m
t2=(L-S1)/v=0.5s
∴t = t1 +t2=1.5s(2)
Wf=μmg S1= 0.2×10 ×3=6 J 或 Wf= 1/2 mv2 - 1/2 mv02 = 1/2 ×(16-4)= 6 J (3)在t1时间内,皮带做匀速运动 S皮带=v t1 =4m
Q= μmg ΔS = μmg(S皮带- S1)=2J
(4)由能量守恒, W=Q+Wf=8J
或W=μmg S皮带=8J
7.由图象可知:当ω≤ω1=4rad/s时,物体在传送带上一直减速,经过B点时的速度为当ω≥ ω2=28rad/s时,物体在传送带上一直加速,
经过B点时的速度为
由 a=μg, v02 - v12 =2μgL v22 – v02 =2μgL
解得μ=0.2 v0=5m/s
(2)由图象可知:当水平速度为1m/s时,水平距离为0.5m,
t=s/v=0.5s h=1/2 gt2=1.25m
(3) ω′ =16rad/s 物体和板碰撞前后的速度都是v′ =ω′ R =4m/s
第一次碰后速度向左,减速到0, 再向右加速到4m/s时第二次碰板
v0=5m/s v皮=ωR =ω/4 vB=s/t=s/0.5
t' =2 v' /a= 2v'/μg =4s
将s- ω图象转化为vB - v皮图象如图示:
当ω≤4rad/s时, v皮≤1m/s, 物体在传送带上一直减速,
当 4rad/s ≤ω≤20 rad/s时, 1m/s ≤v皮 ≤v0=5m/s,
物体在传送带上先减速,然后以ωR匀速运动
当ω=20rad/s时, v皮=5m/s, 物体在传送带上一直匀速,
当20rad/s ≤ω≤28rad/s时, 5m/s ≤v皮≤7m/s,
物体在传送带上先加速,然后以ωR匀速运动
当ω≥28rad/s时, v皮≥ 7m/s, 物体在传送带上一直加速
9.解析:以地面为参考系(下同),设传送带的运动速度为v0,在水平段运输的过程中,小货箱先在滑动摩擦力作用下做匀加速运动,设这段路程为s,所用时间为t,加速度为a,则对小箱有:
在这段时间内,传送带运动的路程为: S0 =v0 t
由以上可得: S0 =2S
用f 表示小箱与传送带之间的滑动摩擦力,
则传送带对小箱做功为
传送带克服小箱对它的摩擦力做功
A0=f S0=2×1/2·mv02
两者之差就是摩擦力做功发出的热量Q=1/2·mv02
[也可直接根据摩擦生热 Q= f △S= f(S0- S)计算]
可见,在小箱加速运动过程中,小箱获得的动能与发热量相等. Q=1/2·mv02
T时间内,电动机输出的功为:W=PT
此功用于增加小箱的动能、势能以及克服摩擦力发热,即:
W=N· [ 1/2·mv02+mgh+Q ]= N· [ mv02+mgh
已知相邻两小箱的距离为L,所以
v0T=NL v0=NL / T
联立,得:
10.解:根据“传送带上有黑色痕迹”可知,煤块与传送带之间发生了相对滑动,煤块的加速度a小于传送带的加速度a0。根据牛顿定律,可得
a=μg
设经历时间t,传送带由静止开始加速到速度等于v0,煤块则由静止加速到v,有
v0=a0t v=at
由于a
设在煤块的速度从0增加到v0的整个过程中,传送带和煤块移动的距离分别为s0和s,有
s0=a0t2+v0t' s=
传送带上留下的黑色痕迹的长度 l=s0-s
由以上各式得l=
11. 分析和解答:(1)设子弹第一次射穿木块后的速度为v/(方向向右),则在第一次射穿木块的过程中,对木块和子弹整体由动量守恒定律(取向右方向为正)得:mv0-Mv1=mv+Mv/,可解得v/=3m/s,其方向应向右.
(2)木块向右滑动中加速度大小为a=g=5m/s2,以速度v/=3m/s向右滑行速度减为零时,所用时间为,显然这之前第二颗子弹仍未射出,所以木块向右运动离A点的最大距离.
(3)木块向右运动到离A点的最大距离之后,经0.4s木块向左作匀加速直线运动,并获得速度v//,v//=a0.4=2m/s,即恰好在与皮带速度相等时第二颗子弹将要射入.注意到这一过程中(即第一个1秒内)木块离A点s1= sm-=0.5m.第二次射入一颗子弹使得木块运动的情况与第一次运动的情况完全相同,即在每一秒的时间里,有一颗子弹击中木块,使木块向右运动0.9m,又向左移动s/==0.4m,每一次木块向右离开A点的距离是0.5m.显然,第16颗子弹恰击中木块时,木块离A端的距离是s2=150.5m=7.5m,第16颗子弹击中木块后,木块再向右运动L- s2=8.3m-7.5m=0.8m<0.9m,木块就从右端B滑出.
由此推算,则经过16次子弹射击后木块应将从B点滑出.
P
Q
Q
P
A
B
A
B
B
A
P
v
h
L
30°
v
P
h
v0
s
A
B
ω/rads-1
s /m
0
4
28
0.5
3.5
B
L
L
A
C
D
图24
ω/rads-1
s /m
0
4
28
0.5
3.5
v皮/ms-1
vB /ms-1
0
1
7
1
7
5
5
ω/rads-1
s /m
0
4
28
0.5
3.5
2.5
20
1.5
16
8
1.0
同课章节目录
