2018高考数学“棘手”问题大归纳与大通透专题2.2+平面向量中的最值问题通关
文档属性
| 名称 | 2018高考数学“棘手”问题大归纳与大通透专题2.2+平面向量中的最值问题通关 |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-16 11:15:58 | ||
图片预览




文档简介
( http: / / www.21cnjy.com )
第一类 与数量积有关的最值
1.在 ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com )是边 ( http: / / www.21cnjy.com )上的两个动点,且 ( http: / / www.21cnjy.com ),则 ( http: / / www.21cnjy.com )的取值范围为( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【答案】A
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
2.在边长为 ( http: / / www.21cnjy.com )的正方形 ( http: / / www.21cnjy.com )中, ( http: / / www.21cnjy.com )为 ( http: / / www.21cnjy.com )的中点,点 ( http: / / www.21cnjy.com )在线段 ( http: / / www.21cnjy.com )上运动,则 ( http: / / www.21cnjy.com )的取值范围是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【答案】C
【解析】将正方形放入如图所示的平面直角坐标系中,设E(x,0),0≤x≤1.又 ( http: / / www.21cnjy.com ),C(1,1),所以 ( http: / / www.21cnjy.com ),
所以 ( http: / / www.21cnjy.com ),
因为0≤x≤1,所以 ( http: / / www.21cnjy.com ),即 ( http: / / www.21cnjy.com )的取值范围是 ( http: / / www.21cnjy.com ).
本题选择C选项.
( http: / / www.21cnjy.com )
3.已知、是函数(其中常数)图象上的两个动点,点,若的最小值为0,则函数的最大值为( )
A. B. C. D.
【答案】B
( http: / / www.21cnjy.com )
4.如图,在直角梯形中, ,点在阴影区域(含边界)中运动,则有的取值范围是( )
( http: / / www.21cnjy.com )
A. B. C. D.
【答案】A
( http: / / www.21cnjy.com )
5.在中, ,点满足,则的最大值为( )
A. B. C. D.
【答案】B
【解析】取AB的中点D,连接CD.
,
所以当时, 的最大值为16.故选B.
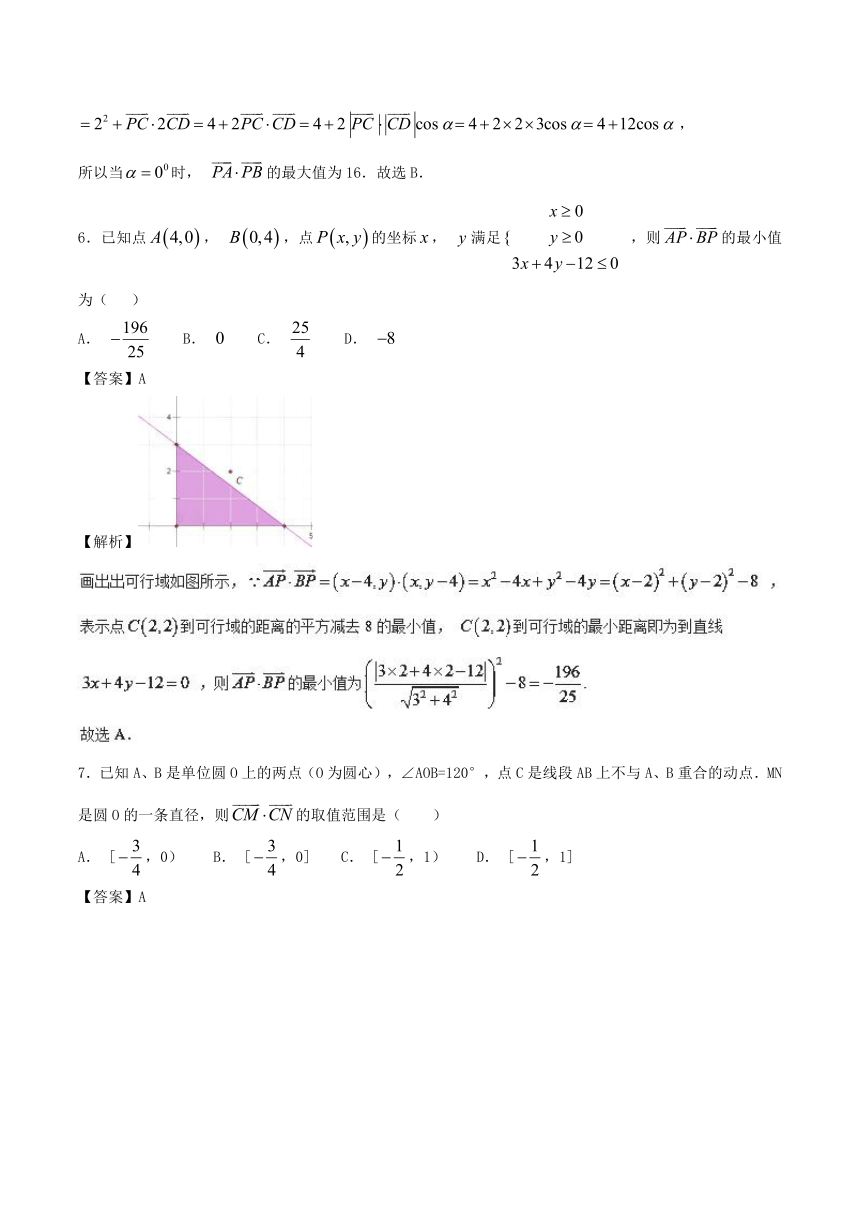
6.已知点, ,点的坐标, 满足,则的最小值为( )
A. B. C. D.
【答案】A
【解析】 ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
7.已知A、B是单位圆O上的两点(O为圆心),∠AOB=120°,点C是线段AB上不与A、B重合的动点.MN是圆O的一条直径,则的取值范围是( )
A. [,0) B. [,0] C. [,1) D. [,1]
【答案】A
【解析】 ( http: / / www.21cnjy.com )
建立如图所示的坐标系, 到直线的距离,则
, 的取值范围是,故选A.
8.在中, ,其面积,则夹角的取值范围为( )
A. B. C. D.
【答案】B
( http: / / www.21cnjy.com )
9.已知是边长为2的等边三角形,P为平面ABC内一点,则的最小值是 ( )
A. B. C. D.
【答案】B
【解析】要取得最小值,则与共线且反向
即位于的中线上,中线长为
设,则
则
当时, 取最小值,
( http: / / www.21cnjy.com )
故选
10.已知则当最小时的值时( )
A. ﹣3 B. 3 C. ﹣1 D. 1
【答案】B
( http: / / www.21cnjy.com )
11.在等腰直角△ABC中,∠ABC=90°,AB=BC=2,M,N(不与A,C重合)为AC边上的两个动点,且满足||=,则的取值范围为( )
A. B. C. D.
【答案】C
【解析】以等腰直角三角形的直角边BC为x轴,BA为y轴,建立平面直角坐标系,如图,则B(0,0),直线AC的方程为x+y=2.
( http: / / www.21cnjy.com )
设M(a,2-a),则0∵0答案:C
12.已知平面向量满足,若,则的最小值为 ( )
A. -2 B. - C. -1 D. 0
【答案】B
( http: / / www.21cnjy.com )
13.在中,边上的中线的长为2,点是所在平面上的任意一点,则的最小值为( )
A. 1 B. 2 C. -2 D. -1
【答案】C
【解析】建立如图所示的平面直角坐标系,使得点D在原点处,点A在y轴上,则.
( http: / / www.21cnjy.com )
设点P的坐标为,则,
故
,当且仅当时等号成立.
所以的最小值为.选C.
14.已知是圆的直径, 是圆的弦上一动点, , ,则的最小值为( )
A. B. C. D.
【答案】D
( http: / / www.21cnjy.com )
15.已知抛物线 ( http: / / www.21cnjy.com )为 ( http: / / www.21cnjy.com )轴负半轴上的动点, ( http: / / www.21cnjy.com )为抛物线的切线, ( http: / / www.21cnjy.com )分别为切点,则 ( http: / / www.21cnjy.com )的最小值为 ( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【答案】C
【解析】设切线 ( http: / / www.21cnjy.com )的方程为 ( http: / / www.21cnjy.com ).
由 ( http: / / www.21cnjy.com ) 消去x整理得 ( http: / / www.21cnjy.com )(*),
∵直线与抛物线相切,
∴ ( http: / / www.21cnjy.com ),故 ( http: / / www.21cnjy.com ).
∴方程 ( http: / / www.21cnjy.com )(*)为 ( http: / / www.21cnjy.com ),解得 ( http: / / www.21cnjy.com ).
∴点 ( http: / / www.21cnjy.com )的坐标分别为 ( http: / / www.21cnjy.com ).
在方程 ( http: / / www.21cnjy.com )中,令 ( http: / / www.21cnjy.com ),可得 ( http: / / www.21cnjy.com ),
∴点 ( http: / / www.21cnjy.com )的坐标为 ( http: / / www.21cnjy.com ).
∴ ( http: / / www.21cnjy.com ),
∴当 ( http: / / www.21cnjy.com )时, ( http: / / www.21cnjy.com )取得最小值 ( http: / / www.21cnjy.com ).选C.
16.已知在直角三角形 ( http: / / www.21cnjy.com )中, ( http: / / www.21cnjy.com )为直角, ( http: / / www.21cnjy.com ),若 ( http: / / www.21cnjy.com )是 ( http: / / www.21cnjy.com )边上的高,点 ( http: / / www.21cnjy.com )在 ( http: / / www.21cnjy.com )内部或边界上运动,则 ( http: / / www.21cnjy.com )的取值范围是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【答案】D
【解析】 ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
17.已知正三角形ABC的边长为2 ( http: / / www.21cnjy.com ),圆O是该三角形的内切圆,P是圆O上的任意一点,则 ( http: / / www.21cnjy.com )的最大值为________.
【答案】1
【解析】在正三角形 ( http: / / www.21cnjy.com )中,内切圆半径 ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ),∴ ( http: / / www.21cnjy.com ),故答案为1.
18.在直角坐标坐标系中,曲线的参数方程为(为参数),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,曲线的极坐标方程.
(1)当时, 交于两点,求;
(2)已知点,点为曲线上任意一点,求的最大值.
【答案】(1);(2).
【解析】试题分析:(1)第(1)问,先把直线的参数方程化为普通方程,再解圆里的三角形得到弦长得到|AB|的值.(2)先写出的三角函数表达式,再利用三角函数求它的最大值.
( http: / / www.21cnjy.com )
(2)设点,则, ,
,又
,
∴的最大值为.
19.已知向量的夹角为锐角,且满足,,若对任意的,都有成立,则的最小值为_______.
【答案】
20.如图,在三角形中, 、分别是边、的中点,点在直线上,且 ,则代数式的最小值为__________.
( http: / / www.21cnjy.com )
【答案】
( http: / / www.21cnjy.com )
结合二次函数的性质可知,当 时,取得最小值为
故答案为.
21.如图,在平行四边形ABCD中, ( http: / / www.21cnjy.com ),边AB,AD的长分别为2,1.若M,N分别是边BC,CD上的点,且满足 ( http: / / www.21cnjy.com ),则 ( http: / / www.21cnjy.com )的取值范围是__________.
( http: / / www.21cnjy.com )
【答案】[2,5]
【解析】 ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
22.已知腰长为2的等腰直角 ( http: / / www.21cnjy.com )中, ( http: / / www.21cnjy.com )为斜边 ( http: / / www.21cnjy.com )的中点,点 ( http: / / www.21cnjy.com )为该平面内一动点,若 ( http: / / www.21cnjy.com ),则 ( http: / / www.21cnjy.com )的最小值为__________.
【答案】 ( http: / / www.21cnjy.com )
【解析】 ( http: / / www.21cnjy.com )
如图建立平面直角坐标系, ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com )
∴ ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ),
当sin ( http: / / www.21cnjy.com )时,得到最小值为 ( http: / / www.21cnjy.com )
故答案为: ( http: / / www.21cnjy.com )
23.已知菱形的边长为2, ,点、分别在边上, , ,若, 则的最小值___________.
【答案】
( http: / / www.21cnjy.com )
24.在等腰梯形 ( http: / / www.21cnjy.com )中,已知 ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ),动点 ( http: / / www.21cnjy.com )分别在线段 ( http: / / www.21cnjy.com )和 ( http: / / www.21cnjy.com )上,且 ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ),则 ( http: / / www.21cnjy.com )的取值范围为______.
【答案】 ( http: / / www.21cnjy.com )
【解析】在等腰梯形 ( http: / / www.21cnjy.com )中,已知 ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ),动点 ( http: / / www.21cnjy.com )分别在线段 ( http: / / www.21cnjy.com )和 ( http: / / www.21cnjy.com )上,且 ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ),则 ( http: / / www.21cnjy.com )的取值范围为
以 ( http: / / www.21cnjy.com )为原点, ( http: / / www.21cnjy.com )为 ( http: / / www.21cnjy.com )轴,建立直角坐标系,过点 ( http: / / www.21cnjy.com )作 ( http: / / www.21cnjy.com ),垂足为 ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ),函数 ( http: / / www.21cnjy.com ) 在 ( http: / / www.21cnjy.com ) 上递减,所 ( http: / / www.21cnjy.com )最大值为 ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com )最小值为 ( http: / / www.21cnjy.com ),即 ( http: / / www.21cnjy.com )的取值范围为 ( http: / / www.21cnjy.com ),故答案为 ( http: / / www.21cnjy.com ).
25.如图,边长为的正三角形放置在平面直角坐标系中, 在轴上,顶点与轴上的定点重合.将正三角形沿轴正方向滚动,即先以顶点为旋转中心顺时针旋转,当顶点落在轴上,再以顶点为旋转中心顺时针旋转,如此继续.当滚动到时,顶点运动轨迹的长度为__________;在滚动过程中, 的最大值为__________.
( http: / / www.21cnjy.com )
【答案】
( http: / / www.21cnjy.com )
26.已知正三角形 ( http: / / www.21cnjy.com )的边长为4, ( http: / / www.21cnjy.com )是平面 ( http: / / www.21cnjy.com )上的动点,且 ( http: / / www.21cnjy.com ),则 ( http: / / www.21cnjy.com )的最大值为_______.
【答案】 ( http: / / www.21cnjy.com )
【解析】如图所示,
( http: / / www.21cnjy.com )
建立直角坐标系,设 ( http: / / www.21cnjy.com ).
由题得, ( http: / / www.21cnjy.com )
所以动点O的轨迹是圆 ( http: / / www.21cnjy.com ),所以 ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ),所以-4x的最大值为 ( http: / / www.21cnjy.com ).
故填 ( http: / / www.21cnjy.com )
27.在平面直角坐标系 ( http: / / www.21cnjy.com )中, ( http: / / www.21cnjy.com ),点 ( http: / / www.21cnjy.com )在圆 ( http: / / www.21cnjy.com )上,若 ( http: / / www.21cnjy.com ),则点 ( http: / / www.21cnjy.com )的横坐标的取值范围是_________.
【答案】 ( http: / / www.21cnjy.com )
【解析】 ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
第二类 与线性分解有关的最值
1.平行四边形中, , , , 是平行四边形内一点,且,如,则的最大值为( )
A. 1 B. 2 C. 3 D. 4
【答案】B
( http: / / www.21cnjy.com )
2.在矩形ABCD中,AB=1,AD=2,动点P在以点C为圆心且与BD相切的圆上.若=λ+μ,则λ+μ的最大值为( )
A. 3 B. 2 C. D. 2
【答案】A
【解析】建立如图所示的直角坐标系,则C点坐标为(2,1).
( http: / / www.21cnjy.com )
设BD与圆C切于点E,连接CE,则CE⊥BD.
∵ CD=1,BC=2,
∴ BD=,
EC,
即圆C的半径为,
( http: / / www.21cnjy.com )
3.已知 ( http: / / www.21cnjy.com )是 ( http: / / www.21cnjy.com )的重心,过点 ( http: / / www.21cnjy.com )作直线 ( http: / / www.21cnjy.com )与 ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com )交于点 ( http: / / www.21cnjy.com ),且 ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ),则 ( http: / / www.21cnjy.com )的最小值是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【答案】D
【解析】 ( http: / / www.21cnjy.com )
如图 ( http: / / www.21cnjy.com ) 三点共线, ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ) ∵ ( http: / / www.21cnjy.com )是 ( http: / / www.21cnjy.com )的重心,
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )解得, ( http: / / www.21cnjy.com ) 结合图象可知 ( http: / / www.21cnjy.com )
令 ( http: / / www.21cnjy.com )
故 ( http: / / www.21cnjy.com )
故 ( http: / / www.21cnjy.com )
当且仅当 ( http: / / www.21cnjy.com )等号成立
故选D
第三类 与向量模长或投影有关的最值
1.设 ( http: / / www.21cnjy.com ),已知两个向量 ( http: / / www.21cnjy.com ),则 ( http: / / www.21cnjy.com )长度的最大值是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【答案】C
( http: / / www.21cnjy.com )
2.定义域为 ( http: / / www.21cnjy.com )的函数 ( http: / / www.21cnjy.com )的图象的两个端点分别为 ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com )是 ( http: / / www.21cnjy.com )图象上任意一点,其中 ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ),向量 ( http: / / www.21cnjy.com ).若不等式 ( http: / / www.21cnjy.com )恒成立,则称函数 ( http: / / www.21cnjy.com )在 ( http: / / www.21cnjy.com )上为“ ( http: / / www.21cnjy.com )函数”.已知函数 ( http: / / www.21cnjy.com )在 ( http: / / www.21cnjy.com )上为“ ( http: / / www.21cnjy.com )函数”,则实数 ( http: / / www.21cnjy.com )的最小值是( )
A. 1 B. 2 C. 3 D. 4
【答案】D
【解析】当x=0时,y=-5,当x=3时,y=1.所以A(0,-5),B(3,1).
所以 ( http: / / www.21cnjy.com ). ( http: / / www.21cnjy.com ).
因为向量 ( http: / / www.21cnjy.com ),所以 ( http: / / www.21cnjy.com ),
所以 ( http: / / www.21cnjy.com ),
所以 ( http: / / www.21cnjy.com )
设 ( http: / / www.21cnjy.com )
所以函数 ( http: / / www.21cnjy.com )在 ( http: / / www.21cnjy.com )单调递增,在( ( http: / / www.21cnjy.com ))上单调递减,所以 ( http: / / www.21cnjy.com )
所以k≥4.故选D.
3.已知 是平面内两个互相垂直的单位向量,若向量满足,则的最大值是( )
A. B. C. D. 2
【答案】A
【解析】 ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
4.在中, , , ,若向量满足,则的最大值与最小值的和为( )
A. 7 B. 8 C. 9 D. 10
【答案】D
【解析】由, , 得,即为直角,以点为原点, 为轴, 为轴建立直角坐标系,则, , ,设的终点坐标为,∵,∴,故的最大值与最小值分别为圆上的点到原点距离的最大值和最小值,故最大值为,最小值为,即之和为10,故选D.
5.已知 ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com )是两个单位向量,则 ( http: / / www.21cnjy.com )的最大值为( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【答案】A
( http: / / www.21cnjy.com )
6.在直角坐标系 ( http: / / www.21cnjy.com )中,已知三点 ( http: / / www.21cnjy.com )若向量 ( http: / / www.21cnjy.com )与 ( http: / / www.21cnjy.com )在向量 ( http: / / www.21cnjy.com )方向上的投影相同,则 ( http: / / www.21cnjy.com )的最小值为( )
A. 2 B. 4 C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【答案】D
【解析】向量 ( http: / / www.21cnjy.com )在向量 ( http: / / www.21cnjy.com )方向上的投影相同, ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com )在直线 ( http: / / www.21cnjy.com )上, ( http: / / www.21cnjy.com )的最小值为原点到直线 ( http: / / www.21cnjy.com )距离的平方,因为 ( http: / / www.21cnjy.com ) ,所以 ( http: / / www.21cnjy.com )的最小值为 ( http: / / www.21cnjy.com ),故选D.
7.已知点在椭圆上,点满足()(是坐标原点),且,则线段在轴上的投影长度的最大值为__________.
【答案】15
( http: / / www.21cnjy.com )
8.点, 分别是椭圆的左、右两焦点,点为椭圆的上顶点,若动点满足:,则的最大值为__________.
【答案】
【解析】设,由,得,则由,可得,化为,可设, , , ,即的最大值为,故答案为.
9.已知 ( http: / / www.21cnjy.com )为圆 ( http: / / www.21cnjy.com )的直径,点 ( http: / / www.21cnjy.com )为直线 ( http: / / www.21cnjy.com )上任意一点,则 ( http: / / www.21cnjy.com )的最小值为__________.
【答案】6
【解析】由圆 ( http: / / www.21cnjy.com )可得,圆的半径为 ( http: / / www.21cnjy.com ) , ( http: / / www.21cnjy.com ),圆心 ( http: / / www.21cnjy.com )到直线 ( http: / / www.21cnjy.com )的距离 ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com )的最小值为 ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ),故答案为 ( http: / / www.21cnjy.com ).
10.已知是平面上一点, , .
①若,则____;
②若,则的最大值为____.
【答案】
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(2)中,因为,
所以,
如图所示,当点是线段的中点时,此时取得最大值,
此时最大值为,所以的最大值为.
( http: / / www.21cnjy.com )
11.已知是平面内两个相互垂直的单位向量,若向量满足,则对于任意的最小值为________.
【答案】
( http: / / www.21cnjy.com )
12.在平面上, ,且, .若,则的取值范围是____________________.
【答案】.
【解析】分别以、为、轴建立直角坐标系,
设,由得.
设,由得, ,
两式相加得,
即,于是,
又 ,故 ,即的取值范围是.
13.在平面上, ,且, , .若,则的取值范围是____________________.
【答案】.
( http: / / www.21cnjy.com )
14.如图,在三角形中, 、分别是边、的中点,点在直线上,且 ,则代数式的最小值为__________.
( http: / / www.21cnjy.com )
【答案】
【解析】不妨设为直角,且,以分别为轴,此时为点的坐标, 表示到原点的距离,最短时为点到直线的距离,由于是中位线,故最短的等于点到距离的一半,即.
15.已知向量,则的最小值为_________
【答案】4
【解析】已知向量,, 当时最小值为4.
故答案为:4.
16.已知为单位向量,且,则的最大值为__________.
【答案】
( http: / / www.21cnjy.com )
17.在△AOB中,G为△AOB的重心,且∠AOB=60°,若=6,则||的最小值是________.
【答案】2
【解析】如图,在△AOB中,
( http: / / www.21cnjy.com )
= =× (+)= (+),
又·=|||·cos60°=6,
∴||||=12,
∴||2= (+)2
= (||2+|2+2·)
= (||2+||2+12)≥×2(||·||+12)=×36=4(当且仅当||=||时取等号).
∴||≥2,故||的最小值是2.
故答案为:2
18.若平面向量, 满足,则在方向上投影的最大值是________.
【答案】
【解析】由可得:
∴
在方向上投影为
故最大值为:
19.已知A,B是圆C1:x2+y2=1上的动点,AB=,P是圆C2:(x-3)2+(y-4)2=1上的动点,则|+|的取值范围为________.
【答案】[7,13]
( http: / / www.21cnjy.com )
故答案为:[7,13]
20.直径的圆上有长度为的动弦,则的最大值为______.
【答案】
【解析】 ( http: / / www.21cnjy.com )
建立如图所示平面直角坐标系,设,则, ,且, ,
,所以当时, 取最大值,故答案为.
21.已知平面向量 ( http: / / www.21cnjy.com )均为单位向量,若 ( http: / / www.21cnjy.com ),则 ( http: / / www.21cnjy.com )的取值范围为__________.
【答案】 ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
22.已知向量a=(sin θ,1),b=(1,cos θ),- <θ<.
(1)若a⊥b,求θ;
(2)求|a+b|的最大值.
【答案】(1)(2)
( http: / / www.21cnjy.com )
第一类 与数量积有关的最值
1.在 ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com )是边 ( http: / / www.21cnjy.com )上的两个动点,且 ( http: / / www.21cnjy.com ),则 ( http: / / www.21cnjy.com )的取值范围为( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【答案】A
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
2.在边长为 ( http: / / www.21cnjy.com )的正方形 ( http: / / www.21cnjy.com )中, ( http: / / www.21cnjy.com )为 ( http: / / www.21cnjy.com )的中点,点 ( http: / / www.21cnjy.com )在线段 ( http: / / www.21cnjy.com )上运动,则 ( http: / / www.21cnjy.com )的取值范围是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【答案】C
【解析】将正方形放入如图所示的平面直角坐标系中,设E(x,0),0≤x≤1.又 ( http: / / www.21cnjy.com ),C(1,1),所以 ( http: / / www.21cnjy.com ),
所以 ( http: / / www.21cnjy.com ),
因为0≤x≤1,所以 ( http: / / www.21cnjy.com ),即 ( http: / / www.21cnjy.com )的取值范围是 ( http: / / www.21cnjy.com ).
本题选择C选项.
( http: / / www.21cnjy.com )
3.已知、是函数(其中常数)图象上的两个动点,点,若的最小值为0,则函数的最大值为( )
A. B. C. D.
【答案】B
( http: / / www.21cnjy.com )
4.如图,在直角梯形中, ,点在阴影区域(含边界)中运动,则有的取值范围是( )
( http: / / www.21cnjy.com )
A. B. C. D.
【答案】A
( http: / / www.21cnjy.com )
5.在中, ,点满足,则的最大值为( )
A. B. C. D.
【答案】B
【解析】取AB的中点D,连接CD.
,
所以当时, 的最大值为16.故选B.
6.已知点, ,点的坐标, 满足,则的最小值为( )
A. B. C. D.
【答案】A
【解析】 ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
7.已知A、B是单位圆O上的两点(O为圆心),∠AOB=120°,点C是线段AB上不与A、B重合的动点.MN是圆O的一条直径,则的取值范围是( )
A. [,0) B. [,0] C. [,1) D. [,1]
【答案】A
【解析】 ( http: / / www.21cnjy.com )
建立如图所示的坐标系, 到直线的距离,则
, 的取值范围是,故选A.
8.在中, ,其面积,则夹角的取值范围为( )
A. B. C. D.
【答案】B
( http: / / www.21cnjy.com )
9.已知是边长为2的等边三角形,P为平面ABC内一点,则的最小值是 ( )
A. B. C. D.
【答案】B
【解析】要取得最小值,则与共线且反向
即位于的中线上,中线长为
设,则
则
当时, 取最小值,
( http: / / www.21cnjy.com )
故选
10.已知则当最小时的值时( )
A. ﹣3 B. 3 C. ﹣1 D. 1
【答案】B
( http: / / www.21cnjy.com )
11.在等腰直角△ABC中,∠ABC=90°,AB=BC=2,M,N(不与A,C重合)为AC边上的两个动点,且满足||=,则的取值范围为( )
A. B. C. D.
【答案】C
【解析】以等腰直角三角形的直角边BC为x轴,BA为y轴,建立平面直角坐标系,如图,则B(0,0),直线AC的方程为x+y=2.
( http: / / www.21cnjy.com )
设M(a,2-a),则0
12.已知平面向量满足,若,则的最小值为 ( )
A. -2 B. - C. -1 D. 0
【答案】B
( http: / / www.21cnjy.com )
13.在中,边上的中线的长为2,点是所在平面上的任意一点,则的最小值为( )
A. 1 B. 2 C. -2 D. -1
【答案】C
【解析】建立如图所示的平面直角坐标系,使得点D在原点处,点A在y轴上,则.
( http: / / www.21cnjy.com )
设点P的坐标为,则,
故
,当且仅当时等号成立.
所以的最小值为.选C.
14.已知是圆的直径, 是圆的弦上一动点, , ,则的最小值为( )
A. B. C. D.
【答案】D
( http: / / www.21cnjy.com )
15.已知抛物线 ( http: / / www.21cnjy.com )为 ( http: / / www.21cnjy.com )轴负半轴上的动点, ( http: / / www.21cnjy.com )为抛物线的切线, ( http: / / www.21cnjy.com )分别为切点,则 ( http: / / www.21cnjy.com )的最小值为 ( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【答案】C
【解析】设切线 ( http: / / www.21cnjy.com )的方程为 ( http: / / www.21cnjy.com ).
由 ( http: / / www.21cnjy.com ) 消去x整理得 ( http: / / www.21cnjy.com )(*),
∵直线与抛物线相切,
∴ ( http: / / www.21cnjy.com ),故 ( http: / / www.21cnjy.com ).
∴方程 ( http: / / www.21cnjy.com )(*)为 ( http: / / www.21cnjy.com ),解得 ( http: / / www.21cnjy.com ).
∴点 ( http: / / www.21cnjy.com )的坐标分别为 ( http: / / www.21cnjy.com ).
在方程 ( http: / / www.21cnjy.com )中,令 ( http: / / www.21cnjy.com ),可得 ( http: / / www.21cnjy.com ),
∴点 ( http: / / www.21cnjy.com )的坐标为 ( http: / / www.21cnjy.com ).
∴ ( http: / / www.21cnjy.com ),
∴当 ( http: / / www.21cnjy.com )时, ( http: / / www.21cnjy.com )取得最小值 ( http: / / www.21cnjy.com ).选C.
16.已知在直角三角形 ( http: / / www.21cnjy.com )中, ( http: / / www.21cnjy.com )为直角, ( http: / / www.21cnjy.com ),若 ( http: / / www.21cnjy.com )是 ( http: / / www.21cnjy.com )边上的高,点 ( http: / / www.21cnjy.com )在 ( http: / / www.21cnjy.com )内部或边界上运动,则 ( http: / / www.21cnjy.com )的取值范围是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【答案】D
【解析】 ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
17.已知正三角形ABC的边长为2 ( http: / / www.21cnjy.com ),圆O是该三角形的内切圆,P是圆O上的任意一点,则 ( http: / / www.21cnjy.com )的最大值为________.
【答案】1
【解析】在正三角形 ( http: / / www.21cnjy.com )中,内切圆半径 ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ),∴ ( http: / / www.21cnjy.com ),故答案为1.
18.在直角坐标坐标系中,曲线的参数方程为(为参数),以坐标原点为极点, 轴的正半轴为极轴建立极坐标系,曲线的极坐标方程.
(1)当时, 交于两点,求;
(2)已知点,点为曲线上任意一点,求的最大值.
【答案】(1);(2).
【解析】试题分析:(1)第(1)问,先把直线的参数方程化为普通方程,再解圆里的三角形得到弦长得到|AB|的值.(2)先写出的三角函数表达式,再利用三角函数求它的最大值.
( http: / / www.21cnjy.com )
(2)设点,则, ,
,又
,
∴的最大值为.
19.已知向量的夹角为锐角,且满足,,若对任意的,都有成立,则的最小值为_______.
【答案】
20.如图,在三角形中, 、分别是边、的中点,点在直线上,且 ,则代数式的最小值为__________.
( http: / / www.21cnjy.com )
【答案】
( http: / / www.21cnjy.com )
结合二次函数的性质可知,当 时,取得最小值为
故答案为.
21.如图,在平行四边形ABCD中, ( http: / / www.21cnjy.com ),边AB,AD的长分别为2,1.若M,N分别是边BC,CD上的点,且满足 ( http: / / www.21cnjy.com ),则 ( http: / / www.21cnjy.com )的取值范围是__________.
( http: / / www.21cnjy.com )
【答案】[2,5]
【解析】 ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
22.已知腰长为2的等腰直角 ( http: / / www.21cnjy.com )中, ( http: / / www.21cnjy.com )为斜边 ( http: / / www.21cnjy.com )的中点,点 ( http: / / www.21cnjy.com )为该平面内一动点,若 ( http: / / www.21cnjy.com ),则 ( http: / / www.21cnjy.com )的最小值为__________.
【答案】 ( http: / / www.21cnjy.com )
【解析】 ( http: / / www.21cnjy.com )
如图建立平面直角坐标系, ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com )
∴ ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ),
当sin ( http: / / www.21cnjy.com )时,得到最小值为 ( http: / / www.21cnjy.com )
故答案为: ( http: / / www.21cnjy.com )
23.已知菱形的边长为2, ,点、分别在边上, , ,若, 则的最小值___________.
【答案】
( http: / / www.21cnjy.com )
24.在等腰梯形 ( http: / / www.21cnjy.com )中,已知 ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ),动点 ( http: / / www.21cnjy.com )分别在线段 ( http: / / www.21cnjy.com )和 ( http: / / www.21cnjy.com )上,且 ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ),则 ( http: / / www.21cnjy.com )的取值范围为______.
【答案】 ( http: / / www.21cnjy.com )
【解析】在等腰梯形 ( http: / / www.21cnjy.com )中,已知 ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ),动点 ( http: / / www.21cnjy.com )分别在线段 ( http: / / www.21cnjy.com )和 ( http: / / www.21cnjy.com )上,且 ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ),则 ( http: / / www.21cnjy.com )的取值范围为
以 ( http: / / www.21cnjy.com )为原点, ( http: / / www.21cnjy.com )为 ( http: / / www.21cnjy.com )轴,建立直角坐标系,过点 ( http: / / www.21cnjy.com )作 ( http: / / www.21cnjy.com ),垂足为 ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ),函数 ( http: / / www.21cnjy.com ) 在 ( http: / / www.21cnjy.com ) 上递减,所 ( http: / / www.21cnjy.com )最大值为 ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com )最小值为 ( http: / / www.21cnjy.com ),即 ( http: / / www.21cnjy.com )的取值范围为 ( http: / / www.21cnjy.com ),故答案为 ( http: / / www.21cnjy.com ).
25.如图,边长为的正三角形放置在平面直角坐标系中, 在轴上,顶点与轴上的定点重合.将正三角形沿轴正方向滚动,即先以顶点为旋转中心顺时针旋转,当顶点落在轴上,再以顶点为旋转中心顺时针旋转,如此继续.当滚动到时,顶点运动轨迹的长度为__________;在滚动过程中, 的最大值为__________.
( http: / / www.21cnjy.com )
【答案】
( http: / / www.21cnjy.com )
26.已知正三角形 ( http: / / www.21cnjy.com )的边长为4, ( http: / / www.21cnjy.com )是平面 ( http: / / www.21cnjy.com )上的动点,且 ( http: / / www.21cnjy.com ),则 ( http: / / www.21cnjy.com )的最大值为_______.
【答案】 ( http: / / www.21cnjy.com )
【解析】如图所示,
( http: / / www.21cnjy.com )
建立直角坐标系,设 ( http: / / www.21cnjy.com ).
由题得, ( http: / / www.21cnjy.com )
所以动点O的轨迹是圆 ( http: / / www.21cnjy.com ),所以 ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ),所以-4x的最大值为 ( http: / / www.21cnjy.com ).
故填 ( http: / / www.21cnjy.com )
27.在平面直角坐标系 ( http: / / www.21cnjy.com )中, ( http: / / www.21cnjy.com ),点 ( http: / / www.21cnjy.com )在圆 ( http: / / www.21cnjy.com )上,若 ( http: / / www.21cnjy.com ),则点 ( http: / / www.21cnjy.com )的横坐标的取值范围是_________.
【答案】 ( http: / / www.21cnjy.com )
【解析】 ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
第二类 与线性分解有关的最值
1.平行四边形中, , , , 是平行四边形内一点,且,如,则的最大值为( )
A. 1 B. 2 C. 3 D. 4
【答案】B
( http: / / www.21cnjy.com )
2.在矩形ABCD中,AB=1,AD=2,动点P在以点C为圆心且与BD相切的圆上.若=λ+μ,则λ+μ的最大值为( )
A. 3 B. 2 C. D. 2
【答案】A
【解析】建立如图所示的直角坐标系,则C点坐标为(2,1).
( http: / / www.21cnjy.com )
设BD与圆C切于点E,连接CE,则CE⊥BD.
∵ CD=1,BC=2,
∴ BD=,
EC,
即圆C的半径为,
( http: / / www.21cnjy.com )
3.已知 ( http: / / www.21cnjy.com )是 ( http: / / www.21cnjy.com )的重心,过点 ( http: / / www.21cnjy.com )作直线 ( http: / / www.21cnjy.com )与 ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com )交于点 ( http: / / www.21cnjy.com ),且 ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ),则 ( http: / / www.21cnjy.com )的最小值是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【答案】D
【解析】 ( http: / / www.21cnjy.com )
如图 ( http: / / www.21cnjy.com ) 三点共线, ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ) ∵ ( http: / / www.21cnjy.com )是 ( http: / / www.21cnjy.com )的重心,
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )解得, ( http: / / www.21cnjy.com ) 结合图象可知 ( http: / / www.21cnjy.com )
令 ( http: / / www.21cnjy.com )
故 ( http: / / www.21cnjy.com )
故 ( http: / / www.21cnjy.com )
当且仅当 ( http: / / www.21cnjy.com )等号成立
故选D
第三类 与向量模长或投影有关的最值
1.设 ( http: / / www.21cnjy.com ),已知两个向量 ( http: / / www.21cnjy.com ),则 ( http: / / www.21cnjy.com )长度的最大值是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【答案】C
( http: / / www.21cnjy.com )
2.定义域为 ( http: / / www.21cnjy.com )的函数 ( http: / / www.21cnjy.com )的图象的两个端点分别为 ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com )是 ( http: / / www.21cnjy.com )图象上任意一点,其中 ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ),向量 ( http: / / www.21cnjy.com ).若不等式 ( http: / / www.21cnjy.com )恒成立,则称函数 ( http: / / www.21cnjy.com )在 ( http: / / www.21cnjy.com )上为“ ( http: / / www.21cnjy.com )函数”.已知函数 ( http: / / www.21cnjy.com )在 ( http: / / www.21cnjy.com )上为“ ( http: / / www.21cnjy.com )函数”,则实数 ( http: / / www.21cnjy.com )的最小值是( )
A. 1 B. 2 C. 3 D. 4
【答案】D
【解析】当x=0时,y=-5,当x=3时,y=1.所以A(0,-5),B(3,1).
所以 ( http: / / www.21cnjy.com ). ( http: / / www.21cnjy.com ).
因为向量 ( http: / / www.21cnjy.com ),所以 ( http: / / www.21cnjy.com ),
所以 ( http: / / www.21cnjy.com ),
所以 ( http: / / www.21cnjy.com )
设 ( http: / / www.21cnjy.com )
所以函数 ( http: / / www.21cnjy.com )在 ( http: / / www.21cnjy.com )单调递增,在( ( http: / / www.21cnjy.com ))上单调递减,所以 ( http: / / www.21cnjy.com )
所以k≥4.故选D.
3.已知 是平面内两个互相垂直的单位向量,若向量满足,则的最大值是( )
A. B. C. D. 2
【答案】A
【解析】 ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
4.在中, , , ,若向量满足,则的最大值与最小值的和为( )
A. 7 B. 8 C. 9 D. 10
【答案】D
【解析】由, , 得,即为直角,以点为原点, 为轴, 为轴建立直角坐标系,则, , ,设的终点坐标为,∵,∴,故的最大值与最小值分别为圆上的点到原点距离的最大值和最小值,故最大值为,最小值为,即之和为10,故选D.
5.已知 ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com )是两个单位向量,则 ( http: / / www.21cnjy.com )的最大值为( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【答案】A
( http: / / www.21cnjy.com )
6.在直角坐标系 ( http: / / www.21cnjy.com )中,已知三点 ( http: / / www.21cnjy.com )若向量 ( http: / / www.21cnjy.com )与 ( http: / / www.21cnjy.com )在向量 ( http: / / www.21cnjy.com )方向上的投影相同,则 ( http: / / www.21cnjy.com )的最小值为( )
A. 2 B. 4 C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
【答案】D
【解析】向量 ( http: / / www.21cnjy.com )在向量 ( http: / / www.21cnjy.com )方向上的投影相同, ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com )在直线 ( http: / / www.21cnjy.com )上, ( http: / / www.21cnjy.com )的最小值为原点到直线 ( http: / / www.21cnjy.com )距离的平方,因为 ( http: / / www.21cnjy.com ) ,所以 ( http: / / www.21cnjy.com )的最小值为 ( http: / / www.21cnjy.com ),故选D.
7.已知点在椭圆上,点满足()(是坐标原点),且,则线段在轴上的投影长度的最大值为__________.
【答案】15
( http: / / www.21cnjy.com )
8.点, 分别是椭圆的左、右两焦点,点为椭圆的上顶点,若动点满足:,则的最大值为__________.
【答案】
【解析】设,由,得,则由,可得,化为,可设, , , ,即的最大值为,故答案为.
9.已知 ( http: / / www.21cnjy.com )为圆 ( http: / / www.21cnjy.com )的直径,点 ( http: / / www.21cnjy.com )为直线 ( http: / / www.21cnjy.com )上任意一点,则 ( http: / / www.21cnjy.com )的最小值为__________.
【答案】6
【解析】由圆 ( http: / / www.21cnjy.com )可得,圆的半径为 ( http: / / www.21cnjy.com ) , ( http: / / www.21cnjy.com ),圆心 ( http: / / www.21cnjy.com )到直线 ( http: / / www.21cnjy.com )的距离 ( http: / / www.21cnjy.com ), ( http: / / www.21cnjy.com )的最小值为 ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com ),故答案为 ( http: / / www.21cnjy.com ).
10.已知是平面上一点, , .
①若,则____;
②若,则的最大值为____.
【答案】
( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com )
(2)中,因为,
所以,
如图所示,当点是线段的中点时,此时取得最大值,
此时最大值为,所以的最大值为.
( http: / / www.21cnjy.com )
11.已知是平面内两个相互垂直的单位向量,若向量满足,则对于任意的最小值为________.
【答案】
( http: / / www.21cnjy.com )
12.在平面上, ,且, .若,则的取值范围是____________________.
【答案】.
【解析】分别以、为、轴建立直角坐标系,
设,由得.
设,由得, ,
两式相加得,
即,于是,
又 ,故 ,即的取值范围是.
13.在平面上, ,且, , .若,则的取值范围是____________________.
【答案】.
( http: / / www.21cnjy.com )
14.如图,在三角形中, 、分别是边、的中点,点在直线上,且 ,则代数式的最小值为__________.
( http: / / www.21cnjy.com )
【答案】
【解析】不妨设为直角,且,以分别为轴,此时为点的坐标, 表示到原点的距离,最短时为点到直线的距离,由于是中位线,故最短的等于点到距离的一半,即.
15.已知向量,则的最小值为_________
【答案】4
【解析】已知向量,, 当时最小值为4.
故答案为:4.
16.已知为单位向量,且,则的最大值为__________.
【答案】
( http: / / www.21cnjy.com )
17.在△AOB中,G为△AOB的重心,且∠AOB=60°,若=6,则||的最小值是________.
【答案】2
【解析】如图,在△AOB中,
( http: / / www.21cnjy.com )
= =× (+)= (+),
又·=|||·cos60°=6,
∴||||=12,
∴||2= (+)2
= (||2+|2+2·)
= (||2+||2+12)≥×2(||·||+12)=×36=4(当且仅当||=||时取等号).
∴||≥2,故||的最小值是2.
故答案为:2
18.若平面向量, 满足,则在方向上投影的最大值是________.
【答案】
【解析】由可得:
∴
在方向上投影为
故最大值为:
19.已知A,B是圆C1:x2+y2=1上的动点,AB=,P是圆C2:(x-3)2+(y-4)2=1上的动点,则|+|的取值范围为________.
【答案】[7,13]
( http: / / www.21cnjy.com )
故答案为:[7,13]
20.直径的圆上有长度为的动弦,则的最大值为______.
【答案】
【解析】 ( http: / / www.21cnjy.com )
建立如图所示平面直角坐标系,设,则, ,且, ,
,所以当时, 取最大值,故答案为.
21.已知平面向量 ( http: / / www.21cnjy.com )均为单位向量,若 ( http: / / www.21cnjy.com ),则 ( http: / / www.21cnjy.com )的取值范围为__________.
【答案】 ( http: / / www.21cnjy.com )
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
22.已知向量a=(sin θ,1),b=(1,cos θ),- <θ<.
(1)若a⊥b,求θ;
(2)求|a+b|的最大值.
【答案】(1)(2)
( http: / / www.21cnjy.com )
同课章节目录
