陕西省黄陵中学2017-2018学年高二(重点班)下学期期中考试数学(文)试题Word版
文档属性
| 名称 | 陕西省黄陵中学2017-2018学年高二(重点班)下学期期中考试数学(文)试题Word版 |

|
|
| 格式 | zip | ||
| 文件大小 | 545.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-17 00:00:00 | ||
图片预览



文档简介
高二重点班数学(文)中期考试试卷
【参考公式或数据】
0.10
0.05
0.010
2.706
3.841
6.635
一、选择题(本大题共12小题,每小题5分,共60分)
1.复数z=i(i+1)(i为虚数单位)的共轭复数是( )
A.-1-i B.-1+i C.1-i D.1+i
2.已知i是虚数单位,若(m+i)2=3-4i,则实数m的值为( )
A.-2 B.±2 C.± D.2
3.若a>b>0,c<d<0,则一定有( )
A.> B.< C.> D.<
4.设x,y∈R,且x+y=5,则3x+3y的最小值为( )
A.10 B.6 C.4 D.18
5.若不等式|x-4|+|x-3|>a对一切实数x恒成立,则实数a的取值范围是( )
A.(-∞,1) B.(1,+∞)
C.(3,4) D.[3,+∞)
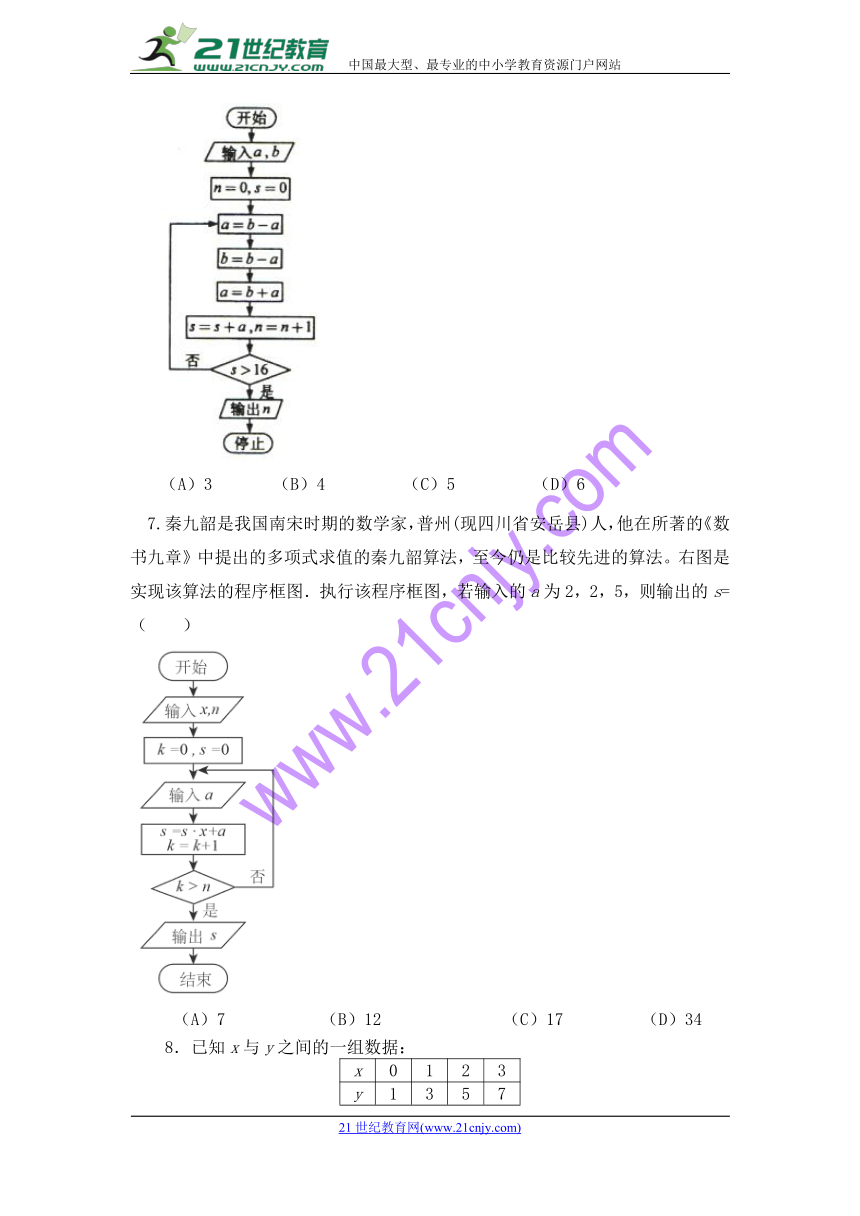
6.执行下图的程序框图,如果输入的a=4,b=6,那么输出的n=
(A)3 (B)4 (C)5 (D)6
7.秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法。右图是实现该算法的程序框图.执行该程序框图,若输入的a为2,2,5,则输出的s=( )21cnjy.com
(A)7 (B)12 (C)17 (D)34
8.已知x与y之间的一组数据:
x
0
1
2
3
y
1
3
5
7
则y与x的线性回归方程=x+必过( )
A.点(2,2) B.点(1.5,0) C.点(1,2) D.点(1.5,4)
9.为了判断高中三年级学生是否选修文科与性别的关系,现随机抽取50名学生,得到如下2×2列联表:
理科
文科
男
13
10
女
7
20
[已知P(K2≥3.841)=0.05,P(K2≥5.024)=0.025]
根据表中数据,得到K2=≈4.844,则认为选修文科与性别有关系出错的可能性为( )
A.5% B.95% C.25% D.97.5%
10.甲、乙两人下棋,两人下成和棋的概率是,甲获胜的概率是,则甲不输的概率为( )
(A) (B) (C) (D)
11.已知 =2, =3, =4,…, =6(a,b均为实数),则推测a,b的值分别是( )
A.a=6,b=18 B.a=6,b=25
C.a=6,b=30 D.a=6,b=35
12.某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40秒.若一名行人来到该路口遇到红灯,则至少需要等待15秒才出现绿灯的概率为( )21·cn·jy·com
(A) (B) (C) (D)
二、填空题(本大题共4小题,每小题5分,共20分)
13.回归直线方程为y=0.575x-14.9,则x=100时,y的估计值为____________.www.21-cn-jy.com
14.i是虚数单位,复数满足,则的实部为_______.
15.用火柴棒摆“金鱼”,如下图所示:
按照上面的规律,第n个“金鱼”图需要火柴棒的根数为________.
16.有三张卡片,分别写有1和2,1和3,2和3. 甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后2·1·c·n·j·y
说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,
丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________________
三、解答题(本大题共6小题,70分)
17.(本小题满分10分)求的值.
18.(本小题满分12分)为考察性别与是否喜欢喝酒之间的关系,在某地随机地抽取160人,其中男性80人,女性80人,女性中有20人喜欢喝酒,另外60人不喜欢喝酒,男性中有50人喜欢喝酒,另外30人不喜欢喝酒.
(1)根据以上数据建立一个2×2的列联表;
(2)判断性别与喝酒是否有关系.
19.(本小题满分12分)若a,b,c∈R+,且a+b+c=1,试用分析法或综合法证明:≥8.【来源:21·世纪·教育·网】
20.(本小题满分12分)已知函数,为不等式的解集.
(Ⅰ)求;
(Ⅱ)证明:当时,.
21.(本小题满分12分)某儿童乐园在“六一”儿童节退出了一项趣味活动.参加活动的儿童需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.设两次记录的数分别为x,y.奖励规则如下:
①若,则奖励玩具一个;
②若,则奖励水杯一个;
③其余情况奖励饮料一瓶.
假设转盘质地均匀,四个区域划分均匀.小亮准备参加此项活动.
(I)求小亮获得玩具的概率;
(II)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.
22.(本小题满分12分)下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图21·世纪*教育网
(Ⅰ)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(Ⅱ)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据:,,,≈2.646.
参考公式:相关系数
回归方程 中斜率和截距的最小二乘估计公式分别为:
参考答案
一 选择题(共12小题,每题5分,总计60分)
1
2
3
4
5
6
7
8
9
10
11
12
B
B
B
B
C
C
C
D
C
C
A
C
二 填空题(共4小题,每题5分,总计20分)
(13 ) (14) > (15) 4,12,36 (16) (0,1]
三.解答与证明题(请写出必要的演算步骤、证明过程。)
17(本小题满分14分)
【解析】在△ABC中,∠CAB=30°,∠CBA=75°,
∴∠ACB=75°,∠ACB=∠ABC.
∴AC=AB=120 m.
∴宽h=AC·sin30°=60(m).
18(本小题满分14分)
【解析】如下图,阴影部分为不等式组所表示的可行域.
设l0:2x+y=0,l:2x+y=z,则z的几何意义是直线y=-2x+z在y轴上的截距,显然,当直线越往上移动,对应在y轴上的截距越大,即z越大;当直线越往下移动,对应在y轴上的截距越小,即z越小.21世纪教育网版权所有
作一族与l0平等的直线系l,经上下平移,可得:当l移动到l1,即过点A(5,2)时,zmax=2×5+2=12;当l移动到l2,即过点B(1,1)时,zmin=2×1+1=3.
19(本小题满分14分)
【解析】当n=1时,a1=S1=3+2=5.
当n≥2时,Sn-1=3+2n-1,
又Sn=3+2n,∴an=Sn-Sn-1=2n-2n-1=2n-1.
又当n=1时,a1=5≠21-1=1,
∴an=
20(本小题满分14分)
【解析】(1)∵m=(2cos,sin),
n=(cos,-2sin),m·n=-1,
∴2cos2-2sin2=-1,∴2cosA=-1,cosA=-
由(1)知cosA=-,结合余弦定理知:
12=4+c2+4c,解得c=2.
21(本小题满分14分)
【解析】(1) 依题意,a1+(a1+a1q)=2(a1+a1q+a1q2),
∵a1≠0, ∴ 2q2+q=0. 解得q=-或q=0(舍)
(2) 由已知可得a1-a1(-)2=3,解得a1=4.
∴Sn==[1-(-)n].
22.(12分)【答案】(Ⅰ),说明与的线性相关程度相当高,从而可以用线性回归模型拟合与的关系;(Ⅱ)1.82亿吨21教育网
【参考公式或数据】
0.10
0.05
0.010
2.706
3.841
6.635
一、选择题(本大题共12小题,每小题5分,共60分)
1.复数z=i(i+1)(i为虚数单位)的共轭复数是( )
A.-1-i B.-1+i C.1-i D.1+i
2.已知i是虚数单位,若(m+i)2=3-4i,则实数m的值为( )
A.-2 B.±2 C.± D.2
3.若a>b>0,c<d<0,则一定有( )
A.> B.< C.> D.<
4.设x,y∈R,且x+y=5,则3x+3y的最小值为( )
A.10 B.6 C.4 D.18
5.若不等式|x-4|+|x-3|>a对一切实数x恒成立,则实数a的取值范围是( )
A.(-∞,1) B.(1,+∞)
C.(3,4) D.[3,+∞)
6.执行下图的程序框图,如果输入的a=4,b=6,那么输出的n=
(A)3 (B)4 (C)5 (D)6
7.秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法。右图是实现该算法的程序框图.执行该程序框图,若输入的a为2,2,5,则输出的s=( )21cnjy.com
(A)7 (B)12 (C)17 (D)34
8.已知x与y之间的一组数据:
x
0
1
2
3
y
1
3
5
7
则y与x的线性回归方程=x+必过( )
A.点(2,2) B.点(1.5,0) C.点(1,2) D.点(1.5,4)
9.为了判断高中三年级学生是否选修文科与性别的关系,现随机抽取50名学生,得到如下2×2列联表:
理科
文科
男
13
10
女
7
20
[已知P(K2≥3.841)=0.05,P(K2≥5.024)=0.025]
根据表中数据,得到K2=≈4.844,则认为选修文科与性别有关系出错的可能性为( )
A.5% B.95% C.25% D.97.5%
10.甲、乙两人下棋,两人下成和棋的概率是,甲获胜的概率是,则甲不输的概率为( )
(A) (B) (C) (D)
11.已知 =2, =3, =4,…, =6(a,b均为实数),则推测a,b的值分别是( )
A.a=6,b=18 B.a=6,b=25
C.a=6,b=30 D.a=6,b=35
12.某路口人行横道的信号灯为红灯和绿灯交替出现,红灯持续时间为40秒.若一名行人来到该路口遇到红灯,则至少需要等待15秒才出现绿灯的概率为( )21·cn·jy·com
(A) (B) (C) (D)
二、填空题(本大题共4小题,每小题5分,共20分)
13.回归直线方程为y=0.575x-14.9,则x=100时,y的估计值为____________.www.21-cn-jy.com
14.i是虚数单位,复数满足,则的实部为_______.
15.用火柴棒摆“金鱼”,如下图所示:
按照上面的规律,第n个“金鱼”图需要火柴棒的根数为________.
16.有三张卡片,分别写有1和2,1和3,2和3. 甲,乙,丙三人各取走一张卡片,甲看了乙的卡片后2·1·c·n·j·y
说:“我与乙的卡片上相同的数字不是2”,乙看了丙的卡片后说:“我与丙的卡片上相同的数字不是1”,
丙说:“我的卡片上的数字之和不是5”,则甲的卡片上的数字是________________
三、解答题(本大题共6小题,70分)
17.(本小题满分10分)求的值.
18.(本小题满分12分)为考察性别与是否喜欢喝酒之间的关系,在某地随机地抽取160人,其中男性80人,女性80人,女性中有20人喜欢喝酒,另外60人不喜欢喝酒,男性中有50人喜欢喝酒,另外30人不喜欢喝酒.
(1)根据以上数据建立一个2×2的列联表;
(2)判断性别与喝酒是否有关系.
19.(本小题满分12分)若a,b,c∈R+,且a+b+c=1,试用分析法或综合法证明:≥8.【来源:21·世纪·教育·网】
20.(本小题满分12分)已知函数,为不等式的解集.
(Ⅰ)求;
(Ⅱ)证明:当时,.
21.(本小题满分12分)某儿童乐园在“六一”儿童节退出了一项趣味活动.参加活动的儿童需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.设两次记录的数分别为x,y.奖励规则如下:
①若,则奖励玩具一个;
②若,则奖励水杯一个;
③其余情况奖励饮料一瓶.
假设转盘质地均匀,四个区域划分均匀.小亮准备参加此项活动.
(I)求小亮获得玩具的概率;
(II)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.
22.(本小题满分12分)下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图21·世纪*教育网
(Ⅰ)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(Ⅱ)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据:,,,≈2.646.
参考公式:相关系数
回归方程 中斜率和截距的最小二乘估计公式分别为:
参考答案
一 选择题(共12小题,每题5分,总计60分)
1
2
3
4
5
6
7
8
9
10
11
12
B
B
B
B
C
C
C
D
C
C
A
C
二 填空题(共4小题,每题5分,总计20分)
(13 ) (14) > (15) 4,12,36 (16) (0,1]
三.解答与证明题(请写出必要的演算步骤、证明过程。)
17(本小题满分14分)
【解析】在△ABC中,∠CAB=30°,∠CBA=75°,
∴∠ACB=75°,∠ACB=∠ABC.
∴AC=AB=120 m.
∴宽h=AC·sin30°=60(m).
18(本小题满分14分)
【解析】如下图,阴影部分为不等式组所表示的可行域.
设l0:2x+y=0,l:2x+y=z,则z的几何意义是直线y=-2x+z在y轴上的截距,显然,当直线越往上移动,对应在y轴上的截距越大,即z越大;当直线越往下移动,对应在y轴上的截距越小,即z越小.21世纪教育网版权所有
作一族与l0平等的直线系l,经上下平移,可得:当l移动到l1,即过点A(5,2)时,zmax=2×5+2=12;当l移动到l2,即过点B(1,1)时,zmin=2×1+1=3.
19(本小题满分14分)
【解析】当n=1时,a1=S1=3+2=5.
当n≥2时,Sn-1=3+2n-1,
又Sn=3+2n,∴an=Sn-Sn-1=2n-2n-1=2n-1.
又当n=1时,a1=5≠21-1=1,
∴an=
20(本小题满分14分)
【解析】(1)∵m=(2cos,sin),
n=(cos,-2sin),m·n=-1,
∴2cos2-2sin2=-1,∴2cosA=-1,cosA=-
由(1)知cosA=-,结合余弦定理知:
12=4+c2+4c,解得c=2.
21(本小题满分14分)
【解析】(1) 依题意,a1+(a1+a1q)=2(a1+a1q+a1q2),
∵a1≠0, ∴ 2q2+q=0. 解得q=-或q=0(舍)
(2) 由已知可得a1-a1(-)2=3,解得a1=4.
∴Sn==[1-(-)n].
22.(12分)【答案】(Ⅰ),说明与的线性相关程度相当高,从而可以用线性回归模型拟合与的关系;(Ⅱ)1.82亿吨21教育网
同课章节目录
