陕西省黄陵中学2017-2018学年高一(普通班)下学期期中考试数学试题Word版
文档属性
| 名称 | 陕西省黄陵中学2017-2018学年高一(普通班)下学期期中考试数学试题Word版 |

|
|
| 格式 | zip | ||
| 文件大小 | 235.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-17 00:00:00 | ||
图片预览



文档简介
高一年级普通班期中考试数学试题
一、选择题:(本大题共12小题,每小题5分,共60分)
1.关于下列几何体,说法正确的是( )
图①是圆柱 B.图②和图③是圆锥
C.图④和图⑤是圆台 D.图⑤是圆台
2. 如图所示,在三棱台A′B′C′-ABC中,截去三棱锥A′-ABC,则剩余部分是( )
A.三棱锥 B.四棱锥 C.三棱柱 D.四棱柱
3.如图所示的直观图是将正方体模型放置在你的水平视线的左下角而绘制的,其中正确的是( )
4.三个平面可把空间分成( )
A.4部分 B.4或6部分
C.4或6或8部分 D.4或6或7或8部分
5.已知不同的直线a,b,c,下列说法正确的是( )
A.a∥b,b∥c,则a∥c
B.a与b异面,b与c异面,则a与c异面
C.a与b相交,b与c相交,则a与c相交
D.a与b所成的角与b与c所成的角相等,则a∥c
6.下列三个命题,其中真命题的个数是( )
①两条直线没有公共点,那么这两条直线平行;
②两个平面如果没有公共点,那么这两个平面平行;
③两个平面都平行于同一条直线,那么这两个平面平行.
A.1 B.2 C.3 D.0
7.正方体ABCD-A1B1C1D1中,P、Q分别是棱AA1与CC1的中点,则经过P、B、Q三点的截面是( )【来源:21·世纪·教育·网】
A.邻边不相等的平行四边形 B.菱形但不是正方形
C.矩形 D.正方形
8.把球的表面积扩大到原来的2倍,那么球的体积扩大到原来的( )
A.2倍 B.倍
C.2倍 D.倍
9.下列说法正确的是( )
A.甲、乙两班期末考试数学平均成绩相同,这表明这两个班数学学习情况一样。
B.期末考试数学成绩的方差甲班比乙班小,这表明甲班的数学学习情况比乙班好。
C.期末考试数学平均成绩甲、乙两班相同,方差甲班比乙班大,则数学学习甲班比乙班好。
D.期末考试数学平均成绩甲、乙两班相同,方差甲班比乙班小,则数学学习甲班比乙班好。
10.下列的流程图示中表示选择结构的是( )
11.对于三种常用的统计图:扇形统计图、折线统计图、条形统计图,下列说法正确的是( )
A.经常可互相转换
B.条形统计图能清楚地反映事物的变化情况
C.扇形统计图能清楚地表示出各部分在总体中所占的百分比
D.折线统计图能清楚地表示出每个项目的具体数目
12. 在算法框图中,表示判断框的图形符号是( )
二、填空题:(本大题共4小题,每小题5分,共20分)
13.一个圆锥的左视图是等腰直角三角形,如图,则圆锥底面的面积为________.
14. 已知PA垂直于平行四边形ABCD所在平面,若PC⊥BD,则平行四边形ABCD的形状是________.www.21-cn-jy.com
15.已知一个表面积为24的正方体,设有一个与每条棱都相切的球,则此球的体积为________.
16..已知样本方差s2= (xi-5)2,则x1+x2+…+x10=__________.
三、解答题: 解答应写出文字说明、证明过程及演算步骤(本大题共6小题,共70分)
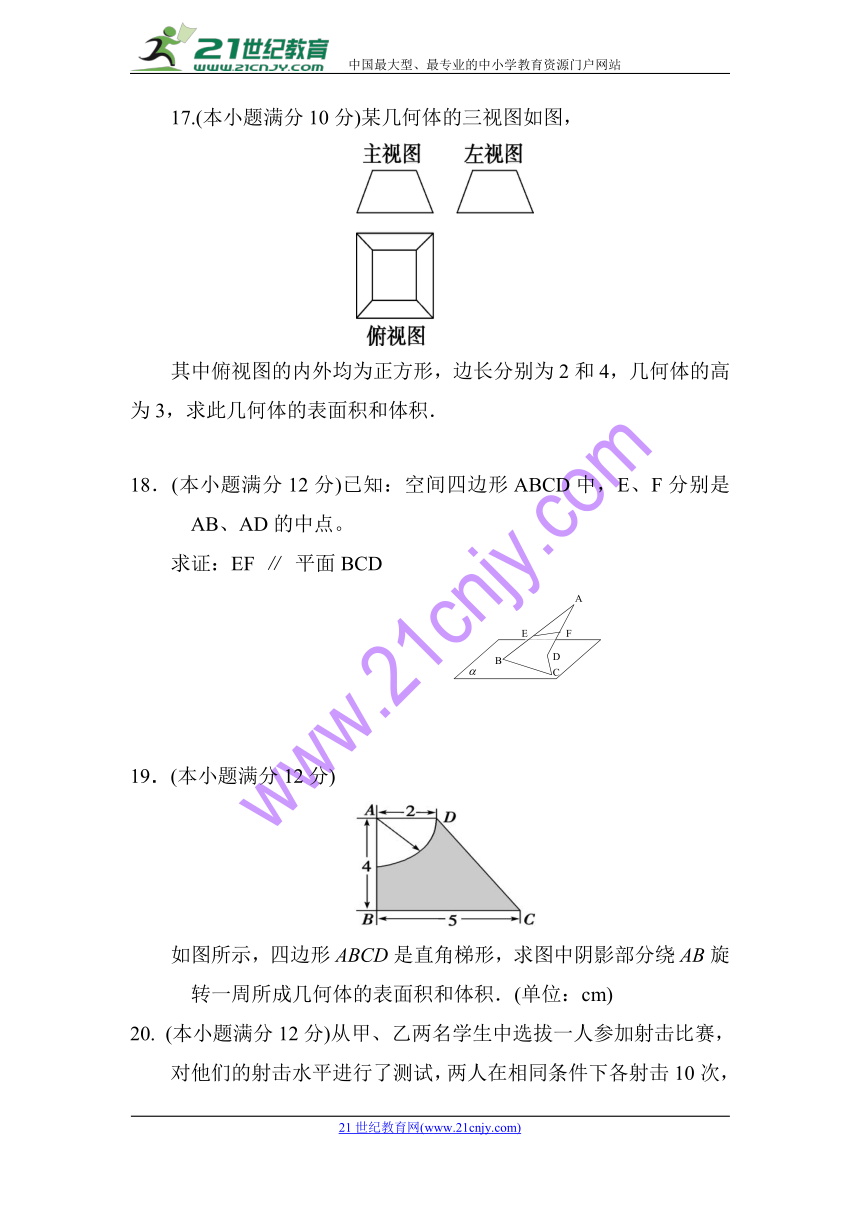
17.(本小题满分10分)某几何体的三视图如图,
其中俯视图的内外均为正方形,边长分别为2和4,几何体的高为3,求此几何体的表面积和体积.
18.(本小题满分12分)已知:空间四边形ABCD中,E、F分别是AB、AD的中点。
求证:EF ∥ 平面BCD
19.(本小题满分12分)
如图所示,四边形ABCD是直角梯形,求图中阴影部分绕AB旋转一周所成几何体的表面积和体积.(单位:cm)
(本小题满分12分)从甲、乙两名学生中选拔一人参加射击比赛,对他们的射击水平进行了测试,两人在相同条件下各射击10次,命中的环数如下:21·cn·jy·com
甲:7,8,6,9,6,5,9,9,7,4.
乙:9,5,7,8,7,6,8,6,7,7.
(1)分别计算甲、乙两人射击命中环数的极差、众数和中位数;
(2)分别计算甲、乙两人射击命中环数的平均数、方差、标准差;
(3)比较两人的成绩,然后决定选择哪一个人参赛.
21.(本小题满分12分)甲、乙两个小组各10名学生的英语口语测试成绩如下(单位:分)
甲组:76 90 84 86 81 87 86 82 85 83
乙组:82 84 85 89 79 80 91 89 79 74
用茎叶图表示两个小组的成绩,并判断哪个小组的成绩更稳定一些.
22 .(本小题满分12分)下列语句运行后,a,b,c的值各等于什么?
a=3; (2) a=3;
b=-5; b=-6;
c=8; c=3;
a=b; a=b;
b=c; b=c;
输出a,b,c.
1-5.DBADA 6-10.ABCDA 11-12.CC
13.2π
14. 菱形.
15.π
16..50
17.
解:依题意得侧面的高
h′= =,
S=S上底+S下底+S侧面
=22+42+4××(2+4)×
=20+12,
所以几何体的表面积为20+12.
体积V=(42+22+2×4)×3=28.
18.
证明:连接BD.
因为AE=EB,AF=FD,所以EF//BD
EF//平面BCD
19.
解:由题意知该几何体的表面积等于圆台下底面积、圆台的侧面积与半球面面积的和.
又S半球面=×4π×22=8π(cm2),
S圆台侧=π(2+5)=35π(cm2),
S圆台下底=π×52=25π(cm2),
所以所成几何体的表面积为
8π+35π+25π=68π(cm2).
由题意知该几何体的体积等于圆台的体积减去半球的体积.
又V圆台=×(22+2×5+52)×4=52π(cm3),
V半球=××23=(cm3),
所以该几何体的体积为
V圆台-V半球=52π-=(cm 已知等差数列{an}满足a2=0,a6+a8=-10.
20.解:(1)对于甲:极差是9-4=5,众数是9,中位数是7;
对于乙:极差是9-5=4,众数是7,中位数是7.
(2)甲==7,
s=[(7-7)2+(8-7)2+(6-7)2+(9-7)2+(6-7)2+(5-7)2+(9-7)2+(9-7)2+(7-7)2+(4-7)2]=2.8,21cnjy.com
s甲==≈1.673;
乙==7,
s=[(9-7)2+(5-7)2+(7-7)2+(8-7)2+(7-7)2+(6-7)2+(8-7)2+(6-7)2+(7-7)2+(7-7)2]=1.2,2·1·c·n·j·y
s乙==≈1.095.
(3)∵甲=乙,s甲>s乙,
∴甲、乙两人的平均成绩相等,乙的成绩比甲的成绩稳定一些,从成绩的稳定性考虑,可以选择乙参赛.
21.解:茎叶图如图所示:
从茎叶图可以看出甲组的数据较为集中,所以甲组的成绩更为稳定一些.
22.解:(1)把b的值-5赋予a(取代a原来的值),把c的值8赋予b(取代b原来的值),c的值不变.所以最后结果为a=-5,b=8,c=8.21世纪教育网版权所有
(2)把b的值-6赋予a,c的值3赋予b,又把a的新值-6赋予c.所以最后结果为a=-5,b=3,c=3.21教育网
一、选择题:(本大题共12小题,每小题5分,共60分)
1.关于下列几何体,说法正确的是( )
图①是圆柱 B.图②和图③是圆锥
C.图④和图⑤是圆台 D.图⑤是圆台
2. 如图所示,在三棱台A′B′C′-ABC中,截去三棱锥A′-ABC,则剩余部分是( )
A.三棱锥 B.四棱锥 C.三棱柱 D.四棱柱
3.如图所示的直观图是将正方体模型放置在你的水平视线的左下角而绘制的,其中正确的是( )
4.三个平面可把空间分成( )
A.4部分 B.4或6部分
C.4或6或8部分 D.4或6或7或8部分
5.已知不同的直线a,b,c,下列说法正确的是( )
A.a∥b,b∥c,则a∥c
B.a与b异面,b与c异面,则a与c异面
C.a与b相交,b与c相交,则a与c相交
D.a与b所成的角与b与c所成的角相等,则a∥c
6.下列三个命题,其中真命题的个数是( )
①两条直线没有公共点,那么这两条直线平行;
②两个平面如果没有公共点,那么这两个平面平行;
③两个平面都平行于同一条直线,那么这两个平面平行.
A.1 B.2 C.3 D.0
7.正方体ABCD-A1B1C1D1中,P、Q分别是棱AA1与CC1的中点,则经过P、B、Q三点的截面是( )【来源:21·世纪·教育·网】
A.邻边不相等的平行四边形 B.菱形但不是正方形
C.矩形 D.正方形
8.把球的表面积扩大到原来的2倍,那么球的体积扩大到原来的( )
A.2倍 B.倍
C.2倍 D.倍
9.下列说法正确的是( )
A.甲、乙两班期末考试数学平均成绩相同,这表明这两个班数学学习情况一样。
B.期末考试数学成绩的方差甲班比乙班小,这表明甲班的数学学习情况比乙班好。
C.期末考试数学平均成绩甲、乙两班相同,方差甲班比乙班大,则数学学习甲班比乙班好。
D.期末考试数学平均成绩甲、乙两班相同,方差甲班比乙班小,则数学学习甲班比乙班好。
10.下列的流程图示中表示选择结构的是( )
11.对于三种常用的统计图:扇形统计图、折线统计图、条形统计图,下列说法正确的是( )
A.经常可互相转换
B.条形统计图能清楚地反映事物的变化情况
C.扇形统计图能清楚地表示出各部分在总体中所占的百分比
D.折线统计图能清楚地表示出每个项目的具体数目
12. 在算法框图中,表示判断框的图形符号是( )
二、填空题:(本大题共4小题,每小题5分,共20分)
13.一个圆锥的左视图是等腰直角三角形,如图,则圆锥底面的面积为________.
14. 已知PA垂直于平行四边形ABCD所在平面,若PC⊥BD,则平行四边形ABCD的形状是________.www.21-cn-jy.com
15.已知一个表面积为24的正方体,设有一个与每条棱都相切的球,则此球的体积为________.
16..已知样本方差s2= (xi-5)2,则x1+x2+…+x10=__________.
三、解答题: 解答应写出文字说明、证明过程及演算步骤(本大题共6小题,共70分)
17.(本小题满分10分)某几何体的三视图如图,
其中俯视图的内外均为正方形,边长分别为2和4,几何体的高为3,求此几何体的表面积和体积.
18.(本小题满分12分)已知:空间四边形ABCD中,E、F分别是AB、AD的中点。
求证:EF ∥ 平面BCD
19.(本小题满分12分)
如图所示,四边形ABCD是直角梯形,求图中阴影部分绕AB旋转一周所成几何体的表面积和体积.(单位:cm)
(本小题满分12分)从甲、乙两名学生中选拔一人参加射击比赛,对他们的射击水平进行了测试,两人在相同条件下各射击10次,命中的环数如下:21·cn·jy·com
甲:7,8,6,9,6,5,9,9,7,4.
乙:9,5,7,8,7,6,8,6,7,7.
(1)分别计算甲、乙两人射击命中环数的极差、众数和中位数;
(2)分别计算甲、乙两人射击命中环数的平均数、方差、标准差;
(3)比较两人的成绩,然后决定选择哪一个人参赛.
21.(本小题满分12分)甲、乙两个小组各10名学生的英语口语测试成绩如下(单位:分)
甲组:76 90 84 86 81 87 86 82 85 83
乙组:82 84 85 89 79 80 91 89 79 74
用茎叶图表示两个小组的成绩,并判断哪个小组的成绩更稳定一些.
22 .(本小题满分12分)下列语句运行后,a,b,c的值各等于什么?
a=3; (2) a=3;
b=-5; b=-6;
c=8; c=3;
a=b; a=b;
b=c; b=c;
输出a,b,c.
1-5.DBADA 6-10.ABCDA 11-12.CC
13.2π
14. 菱形.
15.π
16..50
17.
解:依题意得侧面的高
h′= =,
S=S上底+S下底+S侧面
=22+42+4××(2+4)×
=20+12,
所以几何体的表面积为20+12.
体积V=(42+22+2×4)×3=28.
18.
证明:连接BD.
因为AE=EB,AF=FD,所以EF//BD
EF//平面BCD
19.
解:由题意知该几何体的表面积等于圆台下底面积、圆台的侧面积与半球面面积的和.
又S半球面=×4π×22=8π(cm2),
S圆台侧=π(2+5)=35π(cm2),
S圆台下底=π×52=25π(cm2),
所以所成几何体的表面积为
8π+35π+25π=68π(cm2).
由题意知该几何体的体积等于圆台的体积减去半球的体积.
又V圆台=×(22+2×5+52)×4=52π(cm3),
V半球=××23=(cm3),
所以该几何体的体积为
V圆台-V半球=52π-=(cm 已知等差数列{an}满足a2=0,a6+a8=-10.
20.解:(1)对于甲:极差是9-4=5,众数是9,中位数是7;
对于乙:极差是9-5=4,众数是7,中位数是7.
(2)甲==7,
s=[(7-7)2+(8-7)2+(6-7)2+(9-7)2+(6-7)2+(5-7)2+(9-7)2+(9-7)2+(7-7)2+(4-7)2]=2.8,21cnjy.com
s甲==≈1.673;
乙==7,
s=[(9-7)2+(5-7)2+(7-7)2+(8-7)2+(7-7)2+(6-7)2+(8-7)2+(6-7)2+(7-7)2+(7-7)2]=1.2,2·1·c·n·j·y
s乙==≈1.095.
(3)∵甲=乙,s甲>s乙,
∴甲、乙两人的平均成绩相等,乙的成绩比甲的成绩稳定一些,从成绩的稳定性考虑,可以选择乙参赛.
21.解:茎叶图如图所示:
从茎叶图可以看出甲组的数据较为集中,所以甲组的成绩更为稳定一些.
22.解:(1)把b的值-5赋予a(取代a原来的值),把c的值8赋予b(取代b原来的值),c的值不变.所以最后结果为a=-5,b=8,c=8.21世纪教育网版权所有
(2)把b的值-6赋予a,c的值3赋予b,又把a的新值-6赋予c.所以最后结果为a=-5,b=3,c=3.21教育网
同课章节目录
