4.3 平行线的性质-试卷
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
4.3 平行线的性质
班级:___________姓名:___________得分:__________
(满分:100分,考试时间:40分钟)
一.选择题(共5小题,每题6分,)
1.下列四个图形中,不能推出∠2与∠1相等的是( )
A. B.
C. D.
2.如图,直线a将三角板的直角分为相等的两个角,a∥b,则∠1的度数为( )
A.70° B.105° C.60° D.75°
3.如图,a∥b,含30°角的三角板的直角顶点在直线b上,一个锐角的顶点在直线a上,若∠1=20°,则∠2的度数是( )21世纪教育网版权所有
A.20° B.40° C.50° D.60°
4.如图,AB∥CD,点E在线段BC上,若∠2=70°,∠3=30°,则∠1的度数是( )
A.30° B.40° C.50° D.60°
5.如图,已知AB∥CD,∠1=115°,∠2=65°,则∠C等于( )
A.40° B.45° C.50° D.60°
二.填空题(共5小题,每题6分)
6.如图,AB∥CD,若∠1=60°,则∠2= °.
7.如图,直线EF分别交AB、CD于点E,F,且AB∥CD,若∠1=60°,则∠2= °.
8.如图,两张矩形纸条交叉重叠在一起,若∠1=50°,则∠2的度数为 .
9.将对边平行的纸带折叠成如图所示,已知∠1=52°,则∠α= .
10.如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,则∠AED= .
三.解答题(共5小题,每题8分)
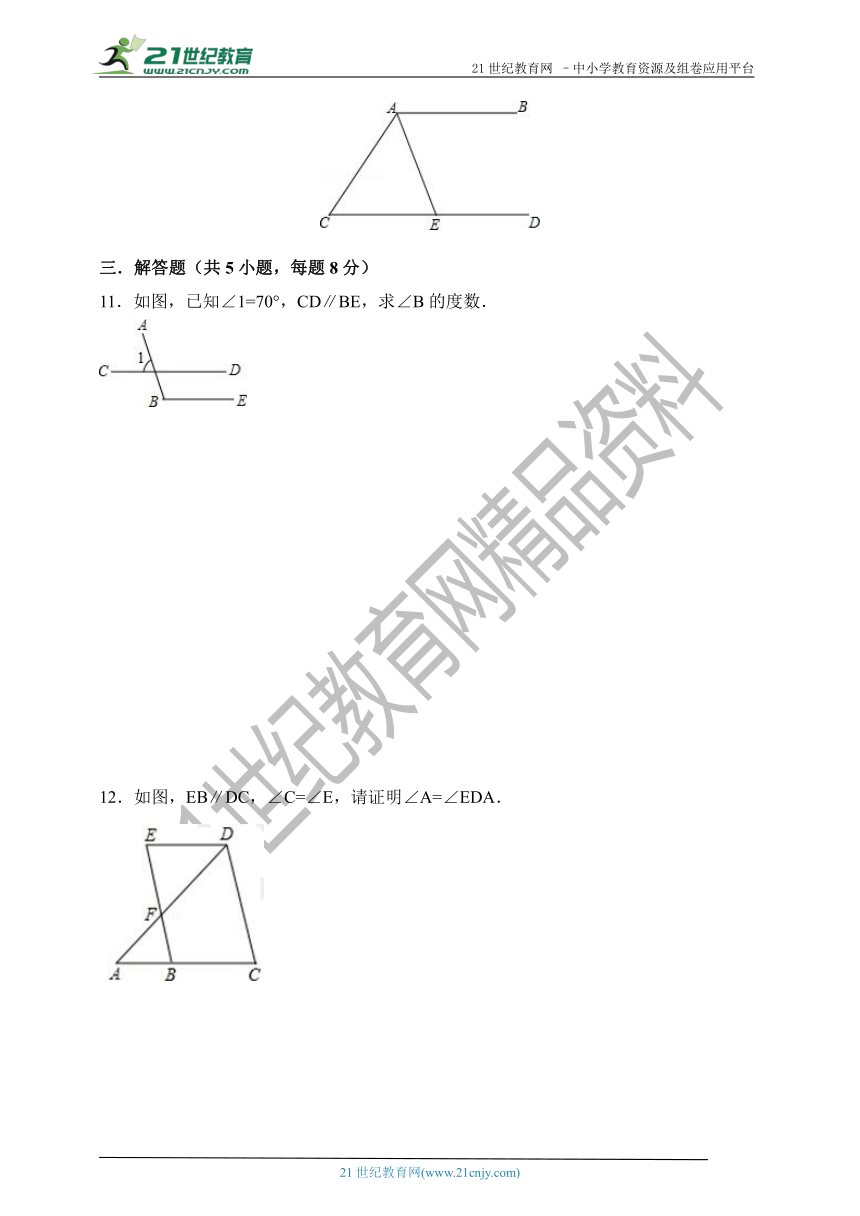
11.如图,已知∠1=70°,CD∥BE,求∠B的度数.
12.如图,EB∥DC,∠C=∠E,请证明∠A=∠EDA.
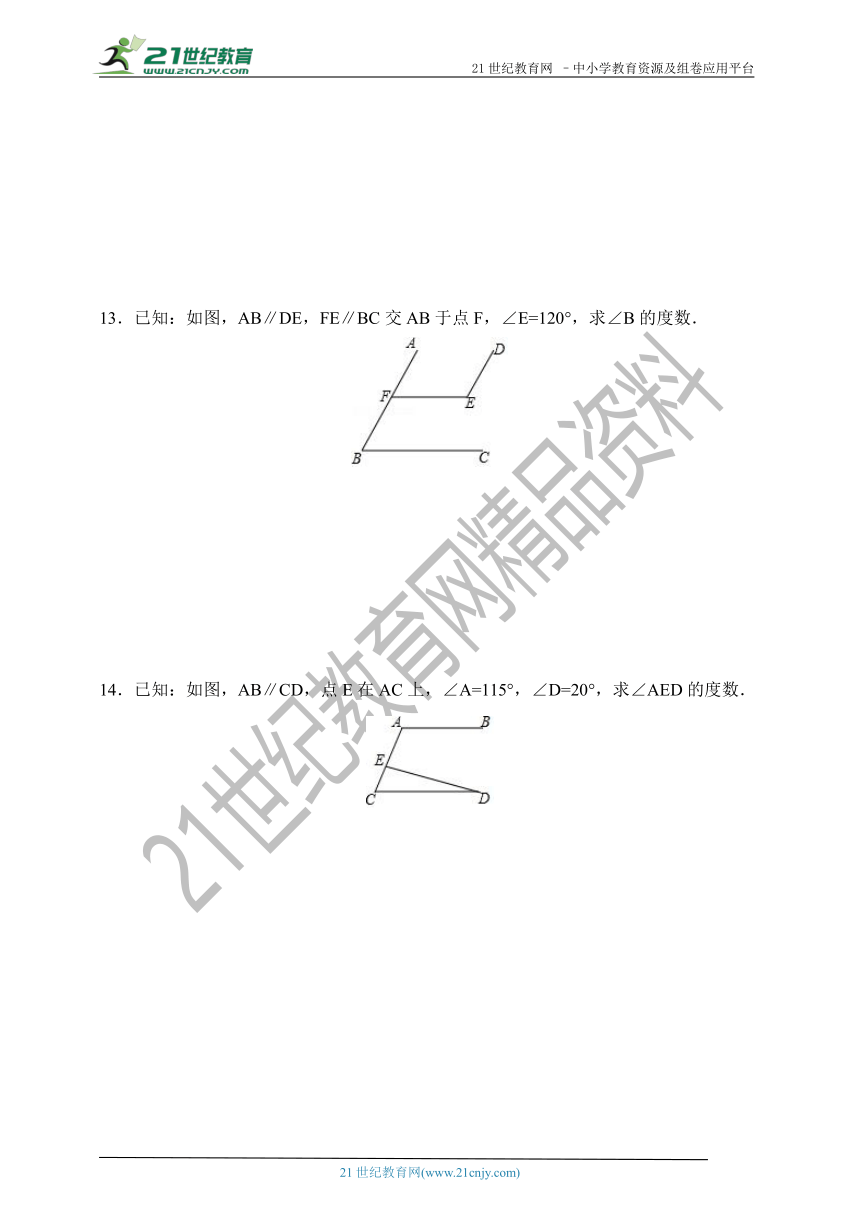
13.已知:如图,AB∥DE,FE∥BC交AB于点F,∠E=120°,求∠B的度数.
14.已知:如图,AB∥CD,点E在AC上,∠A=115°,∠D=20°,求∠AED的度数.
试题解析
一.选择题
1.B
【分析】根据平行线的性质以及对顶角相等的性质进行判断.
【解答】解:A、∵∠1和∠2互为对顶角,∴∠1=∠2,故本选项错误;
B、∵a∥b,∴∠1+∠2=180°(两直线平行,同旁内角互补),不能判断∠1=∠2,故本选项正确;21cnjy.com
C、∵a∥b,∴∠1=∠2(两直线平行,内错角相等),故本选项错误;
D、如图,∵a∥b,∴∠1=∠3(两直线平行,同位角相等),∵∠2=∠3(对顶角相等),∴∠1=∠2,故本选项错误;21·cn·jy·com
故选:B.
【点评】本题考查了平行线的性质,解答本题的关键是掌握平行线的性质:两直线平行,同位角相等,内错角相等,同旁内角互补. www.21-cn-jy.com
2.D
【分析】先根据角平分线的定义以及三角形外角性质,即可得到∠3的度数,再根据平行线的性质,即可得到∠1的度数.2·1·c·n·j·y
【解答】解:∵直线a将三角板的直角分为相等的两个角,
∴∠2=45°,
∵∠3是三角形额外角,
∴∠3=45°+30°=75°,
又∵a∥b,
∴∠1=∠3=75°,
故选:D.
【点评】本题主要考查了平行线的性质的运用,解题时注意:两直线平行,同位角相等.
3.C
【分析】根据a∥b,即可得到∠3=∠2,由三角形外角性质,可得∠3=∠1+30°=20°+30°=50°,进而得到∠2的度数.【来源:21·世纪·教育·网】
【解答】解:如图,∵a∥b,
∴∠3=∠2,
由三角形外角性质,可得∠3=∠1+30°=20°+30°=50°,
∴∠2=50°,
故选:C.
【点评】本题主要考查了平行线的性质,解题时注意:两直线平行,同位角相等.
4.B
【分析】先根据三角形外角的性质求出∠C的度数,再由平行线的性质即可得出∠1的度数.
【解答】解:∵∠2是△CDE的外角,
∴∠C=∠2﹣∠3=70°﹣30°=40°.
∵AB∥CD,
∴∠1=∠C=40°.
故选:B.
【点评】本题考查的是平行线的性质以及三角形外角性质的运用,用到的知识点为:两直线平行,内错角相等.
5.C
【分析】根据两直线平行,同位角相等可得∠1=∠EGD=115°,再根据三角形内角与外角的性质可得∠C的度数.21·世纪*教育网
【解答】解:∵AB∥CD,
∴∠1=∠EGD=115°,
∵∠2=65°,
∴∠C=115°﹣65°=50°,
故选:C.
【点评】此题主要考查了平行线的性质,以及三角形内角与外角的性质,关键是掌握两直线平行,同位角相等.
二.填空题
6. 60 °.
【分析】由平行线的性质可得到∠2=∠1,可求得答案.
【解答】解:∵AB∥CD,
∴∠2=∠1=60°,
故答案为:60.
【点评】本题主要考查平行线的性质,掌握平行线的性质和判定是解题的关键,即两直线平行,同位角相等.
7. 120 °.
【分析】两直线平行,同位角相等,据此可得到∠EFD,然后根据邻补角概念即可求出∠2.
【解答】解:∵AB∥CD,
∴∠DFE=∠1=60°,
∴∠2=180°﹣∠DFE=120°.
故答案为:120.
【点评】本题主要考查了平行线的性质,解题时注意:两直线平行,同位角相等.
8. 130° .
【分析】依据平行线的性质,即可得到∠ABC以及∠2的度数.
【解答】解:∵AD∥BC,AB∥CD,
∴∠1=∠ABC=50°,
∴∠2=180°﹣∠ABC=180°﹣50°=130°,
故答案为:130°.
【点评】本题主要考查了平行线的性质,解题时注意:两直线平行,同位角相等;两直线平行,同旁内角互补.
9. 64° .
【分析】依据∠α=∠3,以及∠1=∠4=52°,即可得到∠α=(180°﹣52°)=64°.
【解答】解:∵对边平行,
∴∠2=∠α,
由折叠可得,∠2=∠3,
∴∠α=∠3,
又∵∠1=∠4=52°,
∴∠α=(180°﹣52°)=64°,
故答案为:64°.
【点评】本题主要考查了平行线的性质,解题时注意:两直线平行,内错角相等.
10. 115° .
【分析】根据平行线性质求出∠CAB的度数,根据角平分线求出∠EAB的度数,根据平行线性质求出∠AED的度数即可.www-2-1-cnjy-com
【解答】解:∵AB∥CD,
∴∠C+∠CAB=180°,
∵∠C=50°,
∴∠CAB=180°﹣50°=130°,
∵AE平分∠CAB,
∴∠EAB=65°,
∵AB∥CD,
∴∠EAB+∠AED=180°,
∴∠AED=180°﹣65°=115°,
故答案为:115°.
【点评】本题考查了角平分线定义和平行线性质的应用,注意:平行线的性质有:①两条平行线被第三条直线所截,同位角相等,②两条平行线被第三条直线所截,内错角相等,③两条平行线被第三条直线所截,同旁内角互补.2-1-c-n-j-y
三.解答题
11.【分析】先根据邻补角的定义求出∠AGD的度数,再由平行线的性质即可得出结论.
【解答】解:如图,∵∠1=70°,
∴∠AGD=180°﹣70°=110°.
∵CD∥BE,
∴∠B=∠AGD=110°.
【点评】本题考查的是平行线的性质以及邻补角定义.用到的知识点为:两直线平行,同位角相等.
12.【分析】先根据两直线平行,同位角相等求出∠C=∠ABE,从而求出∠ABE=∠E,然后根据内错角相等,两直线平行求出AC∥DE,再根据两直线平行,内错角相等即可证明.21*cnjy*com
【解答】证明:∵EB∥DC,
∴∠C=∠ABE(两直线平行,同位角相等),
∵∠C=∠E,
∴∠ABE=∠E,
∴AC∥DE(内错角相等,两直线平行),
∴∠A=∠ADE.
【点评】本题考查了平行线的判定与性质,根据图形准确找出两直线平行的条件是解题的关键.
13.【分析】先根据平行线的性质,得出∠AFE的度数,再根据平行线的性质,即可得到∠B的度数.
【解答】解:∵AB∥DE,∠E=120°,
∴∠AFE=180°﹣∠E=60°,
又∵FE∥BC,
∴∠B=∠AFE=60°.
【点评】本题主要考查了平行线的性质的运用,解题时注意:两直线平行,同旁内角互补,两直线平行,同位角相等.21教育网
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
4.3 平行线的性质
班级:___________姓名:___________得分:__________
(满分:100分,考试时间:40分钟)
一.选择题(共5小题,每题6分,)
1.下列四个图形中,不能推出∠2与∠1相等的是( )
A. B.
C. D.
2.如图,直线a将三角板的直角分为相等的两个角,a∥b,则∠1的度数为( )
A.70° B.105° C.60° D.75°
3.如图,a∥b,含30°角的三角板的直角顶点在直线b上,一个锐角的顶点在直线a上,若∠1=20°,则∠2的度数是( )21世纪教育网版权所有
A.20° B.40° C.50° D.60°
4.如图,AB∥CD,点E在线段BC上,若∠2=70°,∠3=30°,则∠1的度数是( )
A.30° B.40° C.50° D.60°
5.如图,已知AB∥CD,∠1=115°,∠2=65°,则∠C等于( )
A.40° B.45° C.50° D.60°
二.填空题(共5小题,每题6分)
6.如图,AB∥CD,若∠1=60°,则∠2= °.
7.如图,直线EF分别交AB、CD于点E,F,且AB∥CD,若∠1=60°,则∠2= °.
8.如图,两张矩形纸条交叉重叠在一起,若∠1=50°,则∠2的度数为 .
9.将对边平行的纸带折叠成如图所示,已知∠1=52°,则∠α= .
10.如图,AB∥CD,AE平分∠CAB交CD于点E,若∠C=50°,则∠AED= .
三.解答题(共5小题,每题8分)
11.如图,已知∠1=70°,CD∥BE,求∠B的度数.
12.如图,EB∥DC,∠C=∠E,请证明∠A=∠EDA.
13.已知:如图,AB∥DE,FE∥BC交AB于点F,∠E=120°,求∠B的度数.
14.已知:如图,AB∥CD,点E在AC上,∠A=115°,∠D=20°,求∠AED的度数.
试题解析
一.选择题
1.B
【分析】根据平行线的性质以及对顶角相等的性质进行判断.
【解答】解:A、∵∠1和∠2互为对顶角,∴∠1=∠2,故本选项错误;
B、∵a∥b,∴∠1+∠2=180°(两直线平行,同旁内角互补),不能判断∠1=∠2,故本选项正确;21cnjy.com
C、∵a∥b,∴∠1=∠2(两直线平行,内错角相等),故本选项错误;
D、如图,∵a∥b,∴∠1=∠3(两直线平行,同位角相等),∵∠2=∠3(对顶角相等),∴∠1=∠2,故本选项错误;21·cn·jy·com
故选:B.
【点评】本题考查了平行线的性质,解答本题的关键是掌握平行线的性质:两直线平行,同位角相等,内错角相等,同旁内角互补. www.21-cn-jy.com
2.D
【分析】先根据角平分线的定义以及三角形外角性质,即可得到∠3的度数,再根据平行线的性质,即可得到∠1的度数.2·1·c·n·j·y
【解答】解:∵直线a将三角板的直角分为相等的两个角,
∴∠2=45°,
∵∠3是三角形额外角,
∴∠3=45°+30°=75°,
又∵a∥b,
∴∠1=∠3=75°,
故选:D.
【点评】本题主要考查了平行线的性质的运用,解题时注意:两直线平行,同位角相等.
3.C
【分析】根据a∥b,即可得到∠3=∠2,由三角形外角性质,可得∠3=∠1+30°=20°+30°=50°,进而得到∠2的度数.【来源:21·世纪·教育·网】
【解答】解:如图,∵a∥b,
∴∠3=∠2,
由三角形外角性质,可得∠3=∠1+30°=20°+30°=50°,
∴∠2=50°,
故选:C.
【点评】本题主要考查了平行线的性质,解题时注意:两直线平行,同位角相等.
4.B
【分析】先根据三角形外角的性质求出∠C的度数,再由平行线的性质即可得出∠1的度数.
【解答】解:∵∠2是△CDE的外角,
∴∠C=∠2﹣∠3=70°﹣30°=40°.
∵AB∥CD,
∴∠1=∠C=40°.
故选:B.
【点评】本题考查的是平行线的性质以及三角形外角性质的运用,用到的知识点为:两直线平行,内错角相等.
5.C
【分析】根据两直线平行,同位角相等可得∠1=∠EGD=115°,再根据三角形内角与外角的性质可得∠C的度数.21·世纪*教育网
【解答】解:∵AB∥CD,
∴∠1=∠EGD=115°,
∵∠2=65°,
∴∠C=115°﹣65°=50°,
故选:C.
【点评】此题主要考查了平行线的性质,以及三角形内角与外角的性质,关键是掌握两直线平行,同位角相等.
二.填空题
6. 60 °.
【分析】由平行线的性质可得到∠2=∠1,可求得答案.
【解答】解:∵AB∥CD,
∴∠2=∠1=60°,
故答案为:60.
【点评】本题主要考查平行线的性质,掌握平行线的性质和判定是解题的关键,即两直线平行,同位角相等.
7. 120 °.
【分析】两直线平行,同位角相等,据此可得到∠EFD,然后根据邻补角概念即可求出∠2.
【解答】解:∵AB∥CD,
∴∠DFE=∠1=60°,
∴∠2=180°﹣∠DFE=120°.
故答案为:120.
【点评】本题主要考查了平行线的性质,解题时注意:两直线平行,同位角相等.
8. 130° .
【分析】依据平行线的性质,即可得到∠ABC以及∠2的度数.
【解答】解:∵AD∥BC,AB∥CD,
∴∠1=∠ABC=50°,
∴∠2=180°﹣∠ABC=180°﹣50°=130°,
故答案为:130°.
【点评】本题主要考查了平行线的性质,解题时注意:两直线平行,同位角相等;两直线平行,同旁内角互补.
9. 64° .
【分析】依据∠α=∠3,以及∠1=∠4=52°,即可得到∠α=(180°﹣52°)=64°.
【解答】解:∵对边平行,
∴∠2=∠α,
由折叠可得,∠2=∠3,
∴∠α=∠3,
又∵∠1=∠4=52°,
∴∠α=(180°﹣52°)=64°,
故答案为:64°.
【点评】本题主要考查了平行线的性质,解题时注意:两直线平行,内错角相等.
10. 115° .
【分析】根据平行线性质求出∠CAB的度数,根据角平分线求出∠EAB的度数,根据平行线性质求出∠AED的度数即可.www-2-1-cnjy-com
【解答】解:∵AB∥CD,
∴∠C+∠CAB=180°,
∵∠C=50°,
∴∠CAB=180°﹣50°=130°,
∵AE平分∠CAB,
∴∠EAB=65°,
∵AB∥CD,
∴∠EAB+∠AED=180°,
∴∠AED=180°﹣65°=115°,
故答案为:115°.
【点评】本题考查了角平分线定义和平行线性质的应用,注意:平行线的性质有:①两条平行线被第三条直线所截,同位角相等,②两条平行线被第三条直线所截,内错角相等,③两条平行线被第三条直线所截,同旁内角互补.2-1-c-n-j-y
三.解答题
11.【分析】先根据邻补角的定义求出∠AGD的度数,再由平行线的性质即可得出结论.
【解答】解:如图,∵∠1=70°,
∴∠AGD=180°﹣70°=110°.
∵CD∥BE,
∴∠B=∠AGD=110°.
【点评】本题考查的是平行线的性质以及邻补角定义.用到的知识点为:两直线平行,同位角相等.
12.【分析】先根据两直线平行,同位角相等求出∠C=∠ABE,从而求出∠ABE=∠E,然后根据内错角相等,两直线平行求出AC∥DE,再根据两直线平行,内错角相等即可证明.21*cnjy*com
【解答】证明:∵EB∥DC,
∴∠C=∠ABE(两直线平行,同位角相等),
∵∠C=∠E,
∴∠ABE=∠E,
∴AC∥DE(内错角相等,两直线平行),
∴∠A=∠ADE.
【点评】本题考查了平行线的判定与性质,根据图形准确找出两直线平行的条件是解题的关键.
13.【分析】先根据平行线的性质,得出∠AFE的度数,再根据平行线的性质,即可得到∠B的度数.
【解答】解:∵AB∥DE,∠E=120°,
∴∠AFE=180°﹣∠E=60°,
又∵FE∥BC,
∴∠B=∠AFE=60°.
【点评】本题主要考查了平行线的性质的运用,解题时注意:两直线平行,同旁内角互补,两直线平行,同位角相等.21教育网
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
