第二章 匀变速直线运动的研究[上学期]
文档属性
| 名称 | 第二章 匀变速直线运动的研究[上学期] |
|
|
| 格式 | rar | ||
| 文件大小 | 143.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2006-09-28 00:00:00 | ||
图片预览




文档简介
课件中心精品资料 www. 找精品资料 到课件中心
第二章 匀变速直线运动的研究
第1课时 实验:探究小车速度随时间变化的规律
自主知识梳理
1.“探究小车速度随时间变化的规律”的实验器材有____________________________
__________________________________________________________________________.
2.测量各计数点的瞬时速度的方法是:______________________________________。
3.本实验中小车运动的速度图象是__________________________________________。
小车运动速度随时间变化的规律是_______________________________________________。
典型例题解析
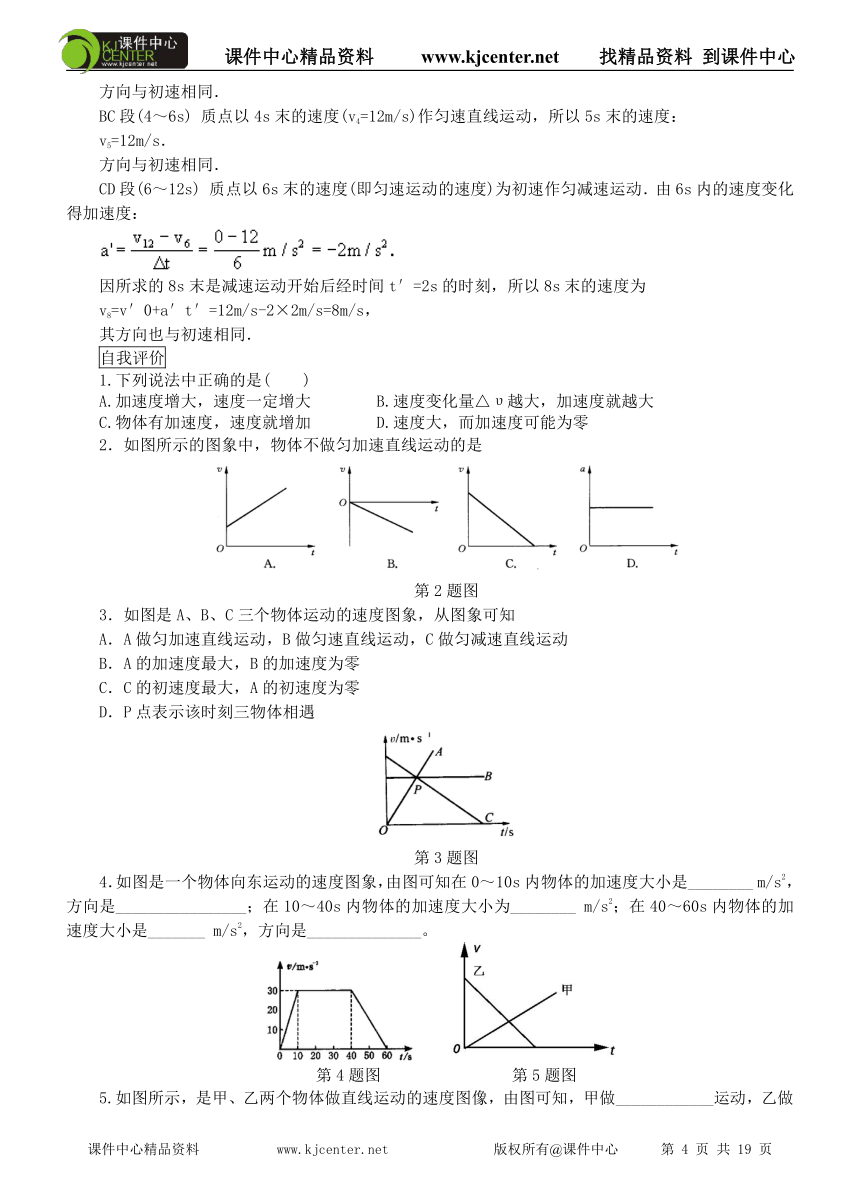
例1:在测定匀变速直线运动的加速度实验中,电火花计时器使用的交流电源频率为50Hz,记录小车做匀速运动的纸带如图所示,在纸带上选择标为0-6的7个记数点,相邻的两个计数点之间还有4个点未画出,纸带旁并排放着带有毫米的刻度尺,零点跟零计数点对齐,由图可读出1、3、5、6四个计数点跟“0”点的距离,请将数值填入表格中,根据所给予数据算出υ1、υ2、υ3、υ4、υ5的值,作出速度—时间图象,并由图象求出小车的平均加速度和小车在0点的速度。
距离 d1 d3 d5 d6
测量值/cm
例1图
解析:根据题目的条件,分别读出计数点1、3、5、6到“0”点的距离,再运用平均速度公式求出第2、3、4点的速度,可进一步根据加速度的定义求出其余各点的速度及加速度。另外也可以根据实验得出的速度作出速度—时间图象,并由图象求出小车的平均加速度和小车在0点的速度。
认真读出1、3、5、6放大图中的读数,填入表中d1=1.20cm,d3=5.40cm,d5=12.00cm,d6=16.20cm,
由中间时刻的速度等于这段位移内的平均速度的定义,先求出:=0.20m/s,
=0.33m/s,
=0.27m/s,
0.15m/s,
0.39m/s,0.45m/s,0.09m/s。将以上6点速度点入速度—时间图象中,连成一条直线(如图所示),要将偏离直线的点对称的均匀分布在直线两侧,由图可读出=0.09m/s,加速度即为直线的斜率:
0.60m/s2。
自我评价
1.在“探究小车速度随时间变化的规律”实验中,对于减小实验误差来说,下列方法中有益的是( )
A.选取测量点,把每打五个点的时间间隔作为一个时间单位
B.使小车运动的加速度尽量小些
C.舍去纸带上密集的点,只利用点迹清晰、点间间隔适当的那一部分进行测量、计算
D.选用各处平整程度、光滑程度相同的长木板做实验
2.利用电火花计时器,研究通过计时器打出的纸带可以分析物体运动的速度和加速度,这一实验能够分析的运动可以是
A.加速直线运动 B.减速直线运动
C.速度方向由负变正,加速度方向恒为正的直线运动
D.速度方向恒为正,加速度方向由负变正的直线运动
3.关于“探究小车速度随时间变化的规律”实验的操作,下列说法中错误的是 ( )
A.长木板不能侧向倾斜,也不能一端高一端低
B.在释放小车前,小车应紧靠在长木板带滑轮的一端
C. 应先接通电源,待打点计时器开始打点后再释放小车
D.要在小车到达定滑轮前使小车停止运动
4.两木块自左向右运动,现用高速摄影机在同一底片上多次曝光,记录下木块每次曝光时的位置,如图所示,连续曝光的时间间隔是相等的,由图可知( )?
第4题图
A.在时刻t2以及时刻t5两木块速度相同?
B.在时刻t3两木块速度相同?
C.在时刻t3和时刻t4之间某瞬时两木块速度相同?
D.在时间t4和时刻t5之间某瞬时两木块速度相同?
5.某同学在测定匀变速运动的加速度时,得到了几条较为理想的纸带,已在每条纸带上每5个打点取好一个计数点,即两计数之间的时间间隔为0.1s,依打点先后编为0,1,2,3,4,5。由于不小心,纸带被撕断了,如图所示,请根据给出的A、B、C、D四段纸带回答(填字母)
第5题图
(1)在B、C、D三段纸带中选出纸带A上撕下的那段应该是 。
(2)打A纸带点1时,物体的速度大小是 cm/s2.
6.某同学做“探究小车速度随时间变化的规律”的实验中得到一条纸带,由每5个连续的点选一个测量点,相邻的两个连续测量点间的距离依次为s1=1.00cm,s2=2.80 Cm,s3=4.70 Cm,s4=6.50 cm,s5=8.40 cm,s6=10.30cm,已知交流电的频率为50Hz,则小车运动的加速度为_________m/s2,打最后一个测量点时物体速度为__________m/s.
7.在“探究小车速度随时间变化的规律”的实验中,某同学操作中有以下实验步骤,其中有错误或遗漏的步骤.(遗漏步骤可编上序号G、H、…)
A.拉住纸带,将小车移至靠近打点计时器处先接通电源,再放开小车;
B.将打点计时器固定在平板上,并接好电路;
C. 把一条细绳拴在小车上,细绳跨过定滑轮,下面吊着适当重的钩码;
D.断开电源,取下纸带;
E.换上新纸带,重复操作三次;
F.将纸带固定在小车尾部,并穿过打点计时器的限位孔.
将以上步骤完善并按合理顺序填写在横线上:
__________________________________.
第2课时 匀变速直线运动速度与时间的关系
自主知识梳理
1. ________________________________________________________________叫匀变速直线运动:
2. 匀变速直线运动的速度公式为_________________________________。
3.匀变速直线运动的速度—时间的图象是_________________________________。
4.加速度与速度图象中的斜率之间的关系如何
典型例题解析
例1:火车沿平直铁轨匀加速前进,通过某一路标时的速度为10.8km/h,1min后变成54km/h,又需经多少时间,火车的速度才能达到64.8km/h?
解析:题中给出了火车在三个不同时刻的瞬时速度,分别设为v1、v2、v3,火车的运动示意图如图所示.由v1、v2和时间t1可以算出火车的加速度a,再用速度公式就可算出.
由:v1=10.8km/h=3m/s,v2=54km/h=15m/s,v3=64.8km/h=18m/s,t1=1min=60s
题后反思:因为在匀变速运动中,速度的变化是均匀的(即加速度恒定),也就是速度的变化量与时间成正比,所以也可以不必求出加速度而直接用比例法求出时间t2.
例2:下图表示一个质点运动的v-t图,试求出该质点在3s末、5s末和8s末的速度.
解析:利用v-t图求速度有两种方法:(1)直接从图上找出所求时刻对应的纵坐标,即得对应的速度值,再根据速度的正负可知此刻的方向;(2)根据图线求出加速度,利用速度公式算出所求时刻的速度.下面用计算法求解.
质点的运动分为三个阶段:
AB段(0~4s )质点作初速v0=6m/s的匀加速运动,由4s内的速度变化得加速度:
所以3s末的速度为
v3=v0+at=6m/s+(1.5×3)m/s=10.5m/s,
方向与初速相同.
BC段(4~6s) 质点以4s末的速度(v4=12m/s)作匀速直线运动,所以5s末的速度:
v5=12m/s.
方向与初速相同.
CD段(6~12s) 质点以6s末的速度(即匀速运动的速度)为初速作匀减速运动.由6s内的速度变化得加速度:
因所求的8s末是减速运动开始后经时间t′=2s的时刻,所以8s末的速度为
v8=v′0+a′t′=12m/s-2×2m/s=8m/s,
其方向也与初速相同.
自我评价
1.下列说法中正确的是( )?
A.加速度增大,速度一定增大 B.速度变化量△υ越大,加速度就越大?
C.物体有加速度,速度就增加 D.速度大,而加速度可能为零?
2.如图所示的图象中,物体不做匀加速直线运动的是
第2题图
3.如图是A、B、C三个物体运动的速度图象,从图象可知
A.A做匀加速直线运动,B做匀速直线运动,C做匀减速直线运动
B.A的加速度最大,B的加速度为零
C.C的初速度最大,A的初速度为零
D.P点表示该时刻三物体相遇
第3题图
4.如图是一个物体向东运动的速度图象,由图可知在0~10s内物体的加速度大小是________ m/s2,方向是________________;在10~40s内物体的加速度大小为________ m/s2;在40~60s内物体的加速度大小是_______ m/s2,方向是______________。
第4题图 第5题图
5.如图所示,是甲、乙两个物体做直线运动的速度图像,由图可知,甲做____________运动,乙做____________运动,它们的加速度大小关系是a甲____________a乙,二者的加速度方向____________.
6.一小球竖直下落,触地时速度为10m/s,触地后又以8m/s的速度竖直弹起,若触地时间是0.05s,小球触地过程中的平均加速度为 .
7. 某汽车以初速度从甲地开出做匀加速直线运动,经过乙地到达丙地的速度为汽车从甲地到乙地的行驶时间等于从乙地到丙地的行驶时间,则汽车经过乙地时的速度多大?
8.某矿井中的升降机,在开始3秒内以1m/s2的加速度,由井底从静止匀加速上升,接着以3秒末的速度匀速上升6秒,最后匀减速上升,又经2秒刚好停在井口,试画出升降机的速度—时间图像,并求井深.?
第3课时 匀变速直线运动位移与时间的关系(一)
自主知识梳理
1.匀速直线运动的位移公式为________________________.
2.匀变速直线运动位移公式______________________________.
3.匀变速直线运动平均速度公式_________________________.
典型例题解析
例1:一辆沿平直公路匀速行驶的汽车,过桥后以1.0m/s2的加速度加速行驶,经12s已离开桥头180m,汽车原来匀速行驶的速度多大?
解析:过桥后,汽车以原来匀速行驶的速度为初速度,作匀加速运动,其运动示意图如图所示.已知a=1.0m/s2,t=12s,s=180m,要求初速.
根据匀加速运动位移公式
说明 解题时,应通过对题意的分析画出示意图,并标注有关物理量,这样会有助于发现其间的相互关系,迅速找到解题的入口.
例2:一辆沿平直路面行驶的汽车,速度为36km/h.刹车后获得加速度的大小是4m/s2,求:(1)刹车后3s末的速度;
(2)从开始刹车至停止,滑行一半距离时的速度.
解析:汽车刹车后作匀减速滑行,其初速度v0=36km/h=10m/s,末速度vt=0,加速度a=-4m/s2.设刹车后滑行ts停止,滑行距离为s,其运动示意图如图2-33所示.
解答 (1)由速度公式vt=v0+at得滑行时间:
即刹车后经2.5s车停止,所以3s末的速度为零.
(2)由位移公式得滑行距离,即
设滑行一半距离至B点时的速度为vB,由推论
说明 (1)不能直接把t=3s代入速度公式计算速度,因为实际滑行时间只有2.5s.求解刹车滑行一类问题,必须先确定实际的滑行时间(或位移);(2)滑行一半距离时的速度不等于滑行过程中的平均速度.
自我评价
1.作初速度为零的匀加速直线运动的物体,将其运动时间顺次分成1∶2∶3的三段,则每段时间内的位移之比为 ( )?
A.1∶3∶5 B.1∶4∶9 C.1∶8∶27 D.1∶16∶81?
2.有一个作匀加速直线运动的物体通过A点和B点时的速度分别为υA和υB.?
(1)通过AB中点C时的速度是 ( )?
A. B.
C. D.以上答案都不对?
(2)设通过AB的时间为t,则在时刻的速度为 ( )?
A. B.
C. D.以上答案都不对?
3.如图所示,完全相同的三块木块并排固定在水平面上,一颗子弹以速度υ水平射入,若子弹在木块中做匀减速直线运动,且穿过第三块木块后速度恰好为零,则子弹依次射入每块木块时的速度之比和穿过每块木块所用时间之比为 ( )?
第3题图
A.υ1∶υ2∶υ3=3∶2∶1 B.υ1∶υ2∶υ3=∶∶1?
C.t1∶t2∶t3=1∶(-1)∶(-) D.t1∶t2∶t3=(-)∶(-1)∶1
4.火车以速度υ1向前行驶,司机突然发现,在其前方同一轨道上距车为s处有另一辆火车,它正沿相同方向以较小的速度υ2做匀速运动,于是他立即使车做匀减速运动,要使两车不致相撞,后面火车的加速度应满足的条件是 .
5.某质点做匀变速直线运动,通过A点时的速度为3m/s。若从A点开始计时,第4s末的速度为11m/s,则该质点的加速度为_______m/s2,在这4s内的位移为________m,第6s初的速度为________m/s。
6.沿平直公路做匀加速直线运动的汽车经过连续三根电线杆的时间间隔分别为3s和2s,已知相邻两电线杆的距离是60m,则汽车的加速度为____________.?
7.一物体做匀变速直线运动,前4s内通过的位移为16m,第6s末的瞬时速度为8m/s,则⑴该物体的初速度和加速度各多大?⑵该物体在第7s内的位移多大?
8.一物体在与初速度相反的恒力作用下做匀变速直线运动,υ0=20m/s,加速度大小a=5m/s2.求?(1)物体经多少时间回到出发点 ?(2)物体回到出发点的速度为多大 ?(3)由开始运动算起,6s末时物体的速度.
第4课时 匀变速直线运动位移与时间的关系(二)
自主知识梳理
1.匀变速直线运动位移和速度的关系式为_________________________.
2.通过进一步的推论可得:(1)在连续相等时间内位移之差为一个___________。
(2)某段时间内中间时刻的瞬时速度________这段时间内的平均速度.(填“大于”、“等于”或“小于”)
典型例题解析
例1:矿井里的升降机,由静止开始匀加速上升,经5s速度达到4m/s后,又以这个速度匀速上升20s,然后匀减速上升,经过4s停在井口,求矿井的深度?
解析:因为升降机从井底到井口的运动分为三段,一般要分别根据匀加速、匀速、匀减速运动的规律进行计算.
1.匀加速上升时:
2.匀速上升时:h2=vt2=4×20=80(m)
3.匀减速上升时:
∴ 矿井的深度h=h1+h2+h3=10+80+8=98(m).
本题如用平均速度来解,就不用求a1、a2,而只要根据平均速度求出、,然后用来进行计算即可。
例2:一列火车进站前先关闭汽阀,让车滑行.滑行了300m时,速度恰减为关闭汽阀时的速度的一半.此后,又继续滑行了20s而停止在车站中.设火车在滑行过程中加速度始终保持不变.试求:(1)火车从关闭汽阀到停止滑行时,滑行的总路程.(2)火车滑行的加速度.(3)火车关闭汽阀时的速度.
解析:画火车运动过程的示意图,本题可把火车的匀减速运动分成二段来考查.
1.以vA的方向为正方向,设加速度为a.
由AB段的条件得:
由BC段的条件得
再把条件vA=2vB代入上式,可解得:
则火车滑行的总路程为:s=s1+s2=300+100=400(m)
2.由BC段得
故火车滑行时的加速度为
负号表示加速度方向与初速度方向相反.
3.由AC段得
故火车关闭汽阀时速度为
自我评价
1.物体做匀变速直线运动,在t时间内通过的路程为s,它在中间位置的速度为υ1,在中间时刻时的速度为υ2,则υ1和υ2的关系正确的是 ( )
A.当物体做匀加速直线运动时,υ1>υ2
B.当物体做匀减速直线运动时,υ1>υ2?
C.当物体做匀速直线运动时,υ1=υ2
D.当物体做匀减速直线运动时,υ1<υ2?
2.物体的初速度为υ0,以不变的加速度a做直线运动,如果要使速度增加到初速度的n倍,则经过的位移是( )?
A.(n2-1) B. (n-1) C.n2 D.(n-1)2?
3.物体做匀变速直线运动,它的位移与时间的关系式为s=4t+4t2,s与t的单位分别是m和s,则物体的初速度与加速度分别为 ( )
A.4m/s,4m/s2 B.4m/s,8m/s2 C.8m/s,4m/s2 D.8m/s,8m/s2
4.机车原来的速度是36km/h,在一段下坡路上得到0.2m/s2的加速度,行驶到坡底的速度为54km/h,则机车下坡所用时间为_______,这段下坡路的长度为__________m。
5.甲、乙两物体在一直线上相距为d,从某一刻起甲做速度为υ的匀速运动,乙做初速度为零,加速度为a的匀加速直线运动,乙在前,甲在后,则甲、乙能相遇一次的条件是____________,甲、乙能相遇两次的条件是____________,甲、乙不能相遇的条件是____________.?
6.火车以15m/s的速度匀速前进,现需在某站临时停车,如果在该站停留时间为1min,火车进站时的加速度大小为a1=0.3m/s2.出站时的加速度大小为a2=0.5m/s2,则火车由于在该站临时停车所延误的时间为 .
7.一辆汽车从静止开始做匀加速直线运动,已知在2s内经过相距27m的A、B两点,汽车经过B点时的速度为15m/s.求:(1)汽车经过A点时的速度大小;(2)A点与出发点间的距离;(3)汽车从出发点到A点的平均速度大小.
???
8.一辆摩托车行驶时能达到的最大速度是30米/秒.现从静止出发,并要求三分钟内追上前面100米处以20米/秒速度匀速前进的汽车,则摩托车的加速度至少为多少 ??
第5课时 自由落体运动
自主知识梳理
1._____________________________________________________________________________________________________________________________叫自由落体运动。
2.自由落体加速度的大小为____________________,方向为______________________。
3.自由落体运动的规律的速度公式为______________,位移公式为_______________。
典型例题解析
例1:从离地500m的空中自由落下一个小球,不计空气阻力,取g=10m/s2,求
(1)经过多少时间落到地面;
(2)从开始落下的时刻起,在第1s内的位移、最后1s内的位移;
(3)落下一半时间的位移.
解析:由h=500m和自由落体加速度,根据位移公式可直接算出落地时间.根据运动时间,可算出第1s内位移和落下一半时间的位移.最后1s内的位移是下落总位移和前(n-1)s下落位移之差.
(1)由,得落地时间
(2)第1s内的位移;
因为从开始运动起前9s内的位移为
所以最后1s内的位移为
h10=h-h9=500m-405m=95m.
(3)落下一半时间即t′=5s,其位移为
例2:一个物体从塔顶上下落,在到达地面前最后1s内通过的位移是整个位移的9/25,求塔高.(g取10m/s2)
解析:设物体下落总时间为t,塔高为h,则
由方程①、②解得
t=5(s)
自我评价
1.下列的那种运动可看成是自由落体运动 ( )?
A.冬季下雪时,雪花的下落
B.从桌边落下的钢笔的运动?
C.从水面自由落到水底的石子的运动
D.跳伞运动员下落的运动?
2.从某建筑物顶自由下落的物体,在落地前的1s内下落的高度为建筑物高的,则物体落到地面的瞬间速度为(g取10m/s2) ( )?
A.10m/s B.15m/s C.20m/s D.25m/s?
3.甲物体从高处自由下落一段时间后,乙物体从同一位置自由下落.若以甲为参考系,则乙物体的运动状态是(甲、乙均未着地) ( )?
A.相对静止 B.向上做匀速直线运动?
C.向下做匀速直线运动 D.向上做匀变速直线运动?
4.物体从高180m处自由下落,把它运动的总时间分成相等的三段,则这三段时间内下落的高度分别为_______m、______m和______m,物体落地时的速度为________m/s。
5.一宇航员在某星球上从高3.2m处自由释放一重物,测得在最初下落1s内所通过的距离为0.8m,则重物下落的总时间是____________,该星球的重力加速度为____________.
6.一矿井深为125m,在井口每隔一定时间自由下落一个小球.当第11个小球刚从井口开始下落,第1个小球刚好到达井底,则相邻小球开始下落的时间间隔为 s;这时第3个小球和第5个小球相距 m.(g取10m/s2)?
7.一条铁链AB长0.49米,系于A端使它竖直下垂,然后让它自由落下,求整条铁链通过悬点下2.45米处的小孔O点时需要的时间.?
8.一座高16m的建筑物屋檐处,每隔一定时间有一滴水落下,当第五滴水离开屋檐时,第一滴水正好落到地面,则此时第三滴水离开地面的高度是多少?(g取10m/s2)
第6课时 伽利略对自由落体运动的研究
自主知识梳理
1.伽利略运用了哪些方法说明了重物与轻物下落得同样快?
2.伽利略得出自由落体运动速度随时间变化的规律是怎样的
3.伽利略科学思想方法的核心是什么
典型例题解析
例1:从一定高度的气球上自由落下两个物体,第一物体下落1s后,第二物体开始下落,两物体用长93.1m的绳连接在一起.问:第二个物体下落多长时间绳被拉紧.
解析:设第二个物体下落ts后绳被拉紧,此时两物体位移差Δh=93.1m
解得 t=9(s)
例2:长5米的铁链,悬其上端。若从悬挂点放开铁链。求铁链经过悬挂点以下25米处所需的时间。
解析:铁链经过悬挂点下面25米处所需的时间,即铁链下落至A1B1到A2B2时所经历的时间(如图)。
设铁链上端A落到A1的时间为t1,落到A2的时间为t2,铁链经过悬挂点以下25米处所需时间为
秒
秒≈0.24秒。
自我评价
1.石块自高为h处的楼房顶自由落下,落地前的速度为v,当石块下落h/4距离时的速度为 ( )
A. B. C. D.
2.做自由落体运动的物体,当它落到全程的一半和全程所用的时间的比是( )?
A. B. C. D.
3.自由下落的物体,自起点开始依次下落三段相等位移所用的时间的比是( )?
A.1∶3∶5 B.1∶4∶9?
C.1∶∶ D.1∶(-1)∶(-)?
4.从塔顶释放一个小球A,1s后从同一个地点再释放一个小球B.设两球都作自由落体运动,则落地前,A、B两球之间的距离 [ ]
A.保持不变. B.不断增大.
C.不断减小. D.有时增大,有时减小.
5.利用水滴下落可以测出重力加速度g:调节水龙头,让水一滴一滴地流出.在水龙头的正下方放一个盘子,调整盘子的高度,使一个水滴碰到盘子时,恰好有一水滴从水龙头开始下落,而空中还有一个正在下落中的水滴.测出水龙头到盘子间距离h.再用秒表测时间,从第一个水滴离开水龙头开始计时,到第N个水滴落至盘中,共用时间为T.第一个水滴到盘子时,第二个水滴离开水龙头的距离是____________,重力加速度g=____________.?
6.在一条软绳两端各结一石块,拿着上端的石块使它与桥面相平,下端石块距桥面3m,放手让石块自由下落,测得两石块落水声相隔0.1s,则桥面距水面 m.(g取10m/s2
7.甲、乙两物体分别从不同高度自由落下,同时落地。已知甲物体自由落下的时间为3s,乙物体自由下落的时间为1s,那么当乙物体开始下落时甲物体距离地面的高度是多少?(g取10m/s2)
8.从离地500m的空中自由落下一个小球,不计空气阻力,取g=10m/s2,求
(1)经过多少时间落到地面;
(2)从开始落下的时刻起,在第1s内的位移、最后1s内的位移;
(3)落下一半时间的位移.
A卷 单元评估
1.一物体从斜面上某点由静止开始作匀加速直线运动,经过3s后到达斜面底端并开始在水平地面上作匀减速直线运动,又经9s停止,则物体在斜面上的位移与水平地面上的位移之比是( )?
A.1∶1 B.1∶2 C.1∶3 D.3∶1?
2.质点作直线运动的v-t图线如图所示,初速度为v0,末速度为v1,则时间t1内的平均速度为
A.
B.
C.
D.无法比较
3.作匀加速直线运动的列车出站时,车头经过站台时的速度为1m/s,车尾经过站台时的速度为7m/s,则列车中部经过站台时的速度为
A.3.5m/s B.4.0m/s C.5.0m/s D.5.5m/s
4.一辆汽车以72km/h的速度沿平直公路匀速前进,司机发现前方有障碍物,立即紧急制动,汽车以5m/s2加速度做匀减速运动,则汽车在制动以后2s内与制动以后6s内的内移之比是( )?
A.1∶1 B.3∶4 C.3∶1 D.4∶3?
5.对做匀加速直线运动的物体,下列说法中正确的是( )?
A.在第1s内、第2s内、第3s内的位移之比一定等于1∶3∶5
B.它的加速度是均匀增加的
C.在相同时间间隔内,它的速度变化量相同
D.在任意两个连续相等时间间隔内通过的位移之差相等
6.甲、乙两车沿平直公路从同一地点同时同向驶向同一目的地,甲车在前一半时间内以速度υ1作匀速运动,后一半时间内以速度υ2作匀速运动,乙车在前一半路程中以υ2作匀速运动,后一半路程中以速度υ1作匀速运动,下面判断中正确的是( )?
A.如果υ1大于υ2,甲车先到达目的地?
B.如果υ1大于υ2,乙车先到达目的地?
C.如果υ1小于υ2,甲车先到达目的地?
D.如果υ1小于υ2,乙车先到达目的地?
7.物体自楼顶处自由落下(不计空气阻力),落到地面的速度为υ.在此过程中,物体从楼顶落到楼高一半处所经历的时间为( )?
A.υ/2 B.υ/(2g) C.υ/(2g) D.2-υ/(2g)
8.足够长的平直的公路上,一辆汽车以a起动时,有一辆匀速行驶的自行车以速度v0从旁驶过,则 ( )
A.汽车追不上自行车,因为汽车起动时速度小
B.以汽车为参考系,自行车是向前作匀减速直线运动
C.汽车与自行车之间的距离开始是不断增加的,直至两者速度相等,然后两者间的距离逐渐减小,直至两车相遇
D.汽车追上自行车的时间是2 v0/a
9.一根木棍保持竖直状态静止不动,在木棍正下方距木棍上端0.8m处有一点A,当木棍由静止释放后,木棍通过A点所用时间是0.2s,不计空气阻力,g取10m/s2,则可知木棍的长度是_______m。
10.在“测定匀变速直线运动的加速度”的实验中,用打点计时器记录纸带运动的时间.计时器所用电源的频率为50Hz,图Ⅱ-4为一次实验得到的一条纸带,纸带上每相邻的两计数点间都有四个点未画出,按时间顺序取0、1、2、3、4、5六个计数点,用米尺量出1、2、3、4、5点到O点的距离如图所示(单位:cm)。由纸带数据计算可得计数点4所代表时刻的瞬时速度大小υ4=__________m/s,小车的加速度大小a=__________m/s2.
第13题图
11.火车正以108km/h的正常速度行驶着,因前方出现意外而临时停车。停车前火车作加速度大小为1m/s2的匀减速运动,1min30s后停止,停止1min后,又以0.5m/s2的加速度起动,作匀加速直线运动,直至速度恢复正常为止。求因临时停车而延误的时间。
12.甲、乙两个物体同时经过某路口向同方向做直线运动,甲以4米/秒的速度做匀速运动,乙从此路口由静止开始以2米/秒2的加速度做匀加速直线运动,问从他们经过路口开始计时多长时间后,他们第一次又相遇,相遇时距路口多远 在相遇前两物体何时距离最大 最大距离是多少 ???????
B卷 单元评估
1.关于质点的位移和路程,下列说法中正确的是( )
A.位移是矢量,位移的方向即质点运动的方向
B.位移的大小不会比路程大
C.路程是标量,即位移的大小
D.当质点作直线运动时,路程等于位移的大小
2.质点以2m/s2的加速度作匀加速运动,下列说法中正确的是( )
A.质点的加速度越来越大
B.质点的速度每经1s增加2m/s
C.质点在任1s内位移比前1s内大2m
D.质点在任1s内的平均速度比前1s内的平均速度大2m/s
3.一物体从斜面顶端由静止开始下滑,经过ts到达斜面中点,此时的速度为υ,则该物体到达斜面底部的时间和速度分别是( )?
A.t, υ B.2t,2υ C. t,2t D.2t, υ?
4.下列运动形式可能的是( )
A.物体的速度很大,但加速度为零
B.物体的速度为零,但加速度很大
C.物体的加速度减小,速度一定减小
D.物体的加速度增大,但速度减小
5.一枚火箭由地面竖直向上发射,其速度如下图所示,则 ( )?
第6题图
A.在B时刻火箭达到最大高度?
B.在C时刻火箭落回地面?
C.在BC段火箭加速度最大
D.在AB段火箭加速度最大?
6.甲、乙、丙三辆汽车以相同的速度v经过同一位置A,随后,甲一直做匀速运动,乙先加速后减速,丙先减速后加速,当它们经过下一个相同位置B时,又具有了相同的速度且仍为v,则( )
A.甲车先通过B点 B.乙车先通过B点
C.甲车最后通过B点 D.丙车最后通过B点
7.如图所示为某郊区部分道路图,一歹徒在A地作案后乘车沿AD道路逃窜,警方同时接到报警信息,并立即由B地乘警车沿道路BE拦截,歹徒到达D点后沿DE道路逃窜,警车恰好在E点追上了歹徒,已知警方与歹徒车辆行驶的速度均为60km/h,AC=4km,BC=6km,DE=5km,则歹徒从A地逃窜至E点被抓获共用时 ( )?
第8题图
A.12min B.10min C.8min D.6min?
8.从某一高度h1处自由落下一物体A,1s后从另一较低高度h2处自由落下另一物体B。若A自由下落45m时赶上B,并再经1s落地,则B从下落到落地共经历的时间约为(g取10m/s2) ( )
A.3s B.3.3s C.3.5s D.4s
9.以12m/s的速度在平直公路上匀速行驶的公共汽车,在距某站牌32m处开始制动,作匀减速直线运动,若加速度大小为2m/s2,行车的方向末变,则它由开始制动到通过站牌所用的时间为________s。(不计汽车的长度)
10.用打点计时器研究匀变速直线运动的规律的实验中,得到一段纸带如图2-42所示,O点为起始点,取A为第一个计数点,以后每5个连续点取为一计数点。则
①打点计时器的连续打两个点的时间间隔为______s,相邻两个计数点的时间间隔为________s;
②若量得OA=4.82cm,OB=6.74cm,OC=8.04cm,OD=9.80cm,OE=12.02cm,则这个运动可能是_________运动,其加速度大小为_____m/s2,B点的速度大小为________m/s,C点的速度大小为_________m/s。
11.某飞机起飞滑行时,从静止开始做匀加速直线运动,加速度大小为4.0m/s2,飞机速度达到80m/s时将离开地面升空。如果在飞机达到起飞速度时,突然接到命令停止起飞,飞行员立即使飞机紧急制动,作匀减速直线运动,加速度的大小为5m/s2。则该飞机场起飞跑道的长度至少多长?
12.一物体从固定斜面的顶端由静止开始匀加速沿斜面下滑,已知物体在斜面上滑行的最初3s通过的路程为s1,物体在斜面上滑行的最后3s,通过的路程为s2,且s2-s1=6m,已知s1∶s2=3∶7,求斜面的长度?
第二章 匀变速直线运动的研究
参考答案与提示
第1课时 实验:探究小车速度随时间变化的规律
自主知识梳理
1.打点计时器;纸带,复写纸片;低压交流电源;小车;细绳;一端附有滑轮的长木板;刻度尺;钩码;两根导线。
2.运用平均速度公式,当较小时即可代表瞬时速度。
3.一条倾斜的直线:速度随时间均匀地增加。
自我评价
1. ACD.
2.ABD
3.B
4.C
5. (1)C (2)33
6.1.86 0.972
7.BFCADE
第2课时 匀变速直线运动速度与时间的关系
自主知识梳理
1.沿着一条直线,且加速度保持不变的运动叫做匀变速直线运动.
2.
3.一条倾斜的直线.
4.对应关系,斜率越大加速度越大.
自我评价
1.D
2.C
3.ABC
4.3m/s2;向东;0;1.5m/s2;向西;
5.初速度为零的匀加速直线运动匀减速直线运动;小于;相反?
6.360m/s2,方向竖直向上?
7. 。
8. 速度—时间图像;井深为25.5米。
第3课时 匀变速直线运动位移与时间的关系(一)
自主知识梳理
1. .
2.
3.
自我评价
1.C
2.(1)C;(2)A
3.D
4.a≥
5.2;28;13
6.4m/s2
7.(1)v0=2m/s a=1m/s2 ⑵
8.(1)8s;(2)20m/s;(3)10m/s与υ0方向相反
第4课时 匀变速直线运动位移与时间的关系(二)
自主知识梳理
1.
2.(1)恒量(2)等于
自我评价
1. ABC
2.A
3.B
4.25s;312.5
5.υ2=2ad;υ2>2ad;υ2<2ad
6.100s?
7.(1)12m/s;(2)48m;(3)6m/s?
8. m/s2??
第6课时 伽利略对自由落体运动的研究
自主知识梳理
1.逻辑推理和实验验证
2.自由落体运动速度随时间是均匀变化的。
3.把实验与逻辑推理和谐地结合起来。
自我评价
1.C
2.C
3.D
4.B
5.;
6.46.51m?
7.(m)
8.(1)10s (2)5m 95m. (3) 125m
A卷 单元评估
1.C
2.B
3.C
4.B
5.CD
6.AC
7.C?
8.BCD
9. 0.6
10.0.405m/s;0.76m/s2?
11.195s
12.4s,16m;2s,4m
B卷 单元评估
1.B
2.BCD
3.A
4.ABD
5.C
6.BD
7.B
8.B
9.4s
10.①0.02;0.1;②匀加速直线;0.46;0.107;0.153
11.1440m
12.12.5m
第3题图
第14题图
课件中心精品资料 www. 版权所有@课件中心 第 19 页 共 19 页
第二章 匀变速直线运动的研究
第1课时 实验:探究小车速度随时间变化的规律
自主知识梳理
1.“探究小车速度随时间变化的规律”的实验器材有____________________________
__________________________________________________________________________.
2.测量各计数点的瞬时速度的方法是:______________________________________。
3.本实验中小车运动的速度图象是__________________________________________。
小车运动速度随时间变化的规律是_______________________________________________。
典型例题解析
例1:在测定匀变速直线运动的加速度实验中,电火花计时器使用的交流电源频率为50Hz,记录小车做匀速运动的纸带如图所示,在纸带上选择标为0-6的7个记数点,相邻的两个计数点之间还有4个点未画出,纸带旁并排放着带有毫米的刻度尺,零点跟零计数点对齐,由图可读出1、3、5、6四个计数点跟“0”点的距离,请将数值填入表格中,根据所给予数据算出υ1、υ2、υ3、υ4、υ5的值,作出速度—时间图象,并由图象求出小车的平均加速度和小车在0点的速度。
距离 d1 d3 d5 d6
测量值/cm
例1图
解析:根据题目的条件,分别读出计数点1、3、5、6到“0”点的距离,再运用平均速度公式求出第2、3、4点的速度,可进一步根据加速度的定义求出其余各点的速度及加速度。另外也可以根据实验得出的速度作出速度—时间图象,并由图象求出小车的平均加速度和小车在0点的速度。
认真读出1、3、5、6放大图中的读数,填入表中d1=1.20cm,d3=5.40cm,d5=12.00cm,d6=16.20cm,
由中间时刻的速度等于这段位移内的平均速度的定义,先求出:=0.20m/s,
=0.33m/s,
=0.27m/s,
0.15m/s,
0.39m/s,0.45m/s,0.09m/s。将以上6点速度点入速度—时间图象中,连成一条直线(如图所示),要将偏离直线的点对称的均匀分布在直线两侧,由图可读出=0.09m/s,加速度即为直线的斜率:
0.60m/s2。
自我评价
1.在“探究小车速度随时间变化的规律”实验中,对于减小实验误差来说,下列方法中有益的是( )
A.选取测量点,把每打五个点的时间间隔作为一个时间单位
B.使小车运动的加速度尽量小些
C.舍去纸带上密集的点,只利用点迹清晰、点间间隔适当的那一部分进行测量、计算
D.选用各处平整程度、光滑程度相同的长木板做实验
2.利用电火花计时器,研究通过计时器打出的纸带可以分析物体运动的速度和加速度,这一实验能够分析的运动可以是
A.加速直线运动 B.减速直线运动
C.速度方向由负变正,加速度方向恒为正的直线运动
D.速度方向恒为正,加速度方向由负变正的直线运动
3.关于“探究小车速度随时间变化的规律”实验的操作,下列说法中错误的是 ( )
A.长木板不能侧向倾斜,也不能一端高一端低
B.在释放小车前,小车应紧靠在长木板带滑轮的一端
C. 应先接通电源,待打点计时器开始打点后再释放小车
D.要在小车到达定滑轮前使小车停止运动
4.两木块自左向右运动,现用高速摄影机在同一底片上多次曝光,记录下木块每次曝光时的位置,如图所示,连续曝光的时间间隔是相等的,由图可知( )?
第4题图
A.在时刻t2以及时刻t5两木块速度相同?
B.在时刻t3两木块速度相同?
C.在时刻t3和时刻t4之间某瞬时两木块速度相同?
D.在时间t4和时刻t5之间某瞬时两木块速度相同?
5.某同学在测定匀变速运动的加速度时,得到了几条较为理想的纸带,已在每条纸带上每5个打点取好一个计数点,即两计数之间的时间间隔为0.1s,依打点先后编为0,1,2,3,4,5。由于不小心,纸带被撕断了,如图所示,请根据给出的A、B、C、D四段纸带回答(填字母)
第5题图
(1)在B、C、D三段纸带中选出纸带A上撕下的那段应该是 。
(2)打A纸带点1时,物体的速度大小是 cm/s2.
6.某同学做“探究小车速度随时间变化的规律”的实验中得到一条纸带,由每5个连续的点选一个测量点,相邻的两个连续测量点间的距离依次为s1=1.00cm,s2=2.80 Cm,s3=4.70 Cm,s4=6.50 cm,s5=8.40 cm,s6=10.30cm,已知交流电的频率为50Hz,则小车运动的加速度为_________m/s2,打最后一个测量点时物体速度为__________m/s.
7.在“探究小车速度随时间变化的规律”的实验中,某同学操作中有以下实验步骤,其中有错误或遗漏的步骤.(遗漏步骤可编上序号G、H、…)
A.拉住纸带,将小车移至靠近打点计时器处先接通电源,再放开小车;
B.将打点计时器固定在平板上,并接好电路;
C. 把一条细绳拴在小车上,细绳跨过定滑轮,下面吊着适当重的钩码;
D.断开电源,取下纸带;
E.换上新纸带,重复操作三次;
F.将纸带固定在小车尾部,并穿过打点计时器的限位孔.
将以上步骤完善并按合理顺序填写在横线上:
__________________________________.
第2课时 匀变速直线运动速度与时间的关系
自主知识梳理
1. ________________________________________________________________叫匀变速直线运动:
2. 匀变速直线运动的速度公式为_________________________________。
3.匀变速直线运动的速度—时间的图象是_________________________________。
4.加速度与速度图象中的斜率之间的关系如何
典型例题解析
例1:火车沿平直铁轨匀加速前进,通过某一路标时的速度为10.8km/h,1min后变成54km/h,又需经多少时间,火车的速度才能达到64.8km/h?
解析:题中给出了火车在三个不同时刻的瞬时速度,分别设为v1、v2、v3,火车的运动示意图如图所示.由v1、v2和时间t1可以算出火车的加速度a,再用速度公式就可算出.
由:v1=10.8km/h=3m/s,v2=54km/h=15m/s,v3=64.8km/h=18m/s,t1=1min=60s
题后反思:因为在匀变速运动中,速度的变化是均匀的(即加速度恒定),也就是速度的变化量与时间成正比,所以也可以不必求出加速度而直接用比例法求出时间t2.
例2:下图表示一个质点运动的v-t图,试求出该质点在3s末、5s末和8s末的速度.
解析:利用v-t图求速度有两种方法:(1)直接从图上找出所求时刻对应的纵坐标,即得对应的速度值,再根据速度的正负可知此刻的方向;(2)根据图线求出加速度,利用速度公式算出所求时刻的速度.下面用计算法求解.
质点的运动分为三个阶段:
AB段(0~4s )质点作初速v0=6m/s的匀加速运动,由4s内的速度变化得加速度:
所以3s末的速度为
v3=v0+at=6m/s+(1.5×3)m/s=10.5m/s,
方向与初速相同.
BC段(4~6s) 质点以4s末的速度(v4=12m/s)作匀速直线运动,所以5s末的速度:
v5=12m/s.
方向与初速相同.
CD段(6~12s) 质点以6s末的速度(即匀速运动的速度)为初速作匀减速运动.由6s内的速度变化得加速度:
因所求的8s末是减速运动开始后经时间t′=2s的时刻,所以8s末的速度为
v8=v′0+a′t′=12m/s-2×2m/s=8m/s,
其方向也与初速相同.
自我评价
1.下列说法中正确的是( )?
A.加速度增大,速度一定增大 B.速度变化量△υ越大,加速度就越大?
C.物体有加速度,速度就增加 D.速度大,而加速度可能为零?
2.如图所示的图象中,物体不做匀加速直线运动的是
第2题图
3.如图是A、B、C三个物体运动的速度图象,从图象可知
A.A做匀加速直线运动,B做匀速直线运动,C做匀减速直线运动
B.A的加速度最大,B的加速度为零
C.C的初速度最大,A的初速度为零
D.P点表示该时刻三物体相遇
第3题图
4.如图是一个物体向东运动的速度图象,由图可知在0~10s内物体的加速度大小是________ m/s2,方向是________________;在10~40s内物体的加速度大小为________ m/s2;在40~60s内物体的加速度大小是_______ m/s2,方向是______________。
第4题图 第5题图
5.如图所示,是甲、乙两个物体做直线运动的速度图像,由图可知,甲做____________运动,乙做____________运动,它们的加速度大小关系是a甲____________a乙,二者的加速度方向____________.
6.一小球竖直下落,触地时速度为10m/s,触地后又以8m/s的速度竖直弹起,若触地时间是0.05s,小球触地过程中的平均加速度为 .
7. 某汽车以初速度从甲地开出做匀加速直线运动,经过乙地到达丙地的速度为汽车从甲地到乙地的行驶时间等于从乙地到丙地的行驶时间,则汽车经过乙地时的速度多大?
8.某矿井中的升降机,在开始3秒内以1m/s2的加速度,由井底从静止匀加速上升,接着以3秒末的速度匀速上升6秒,最后匀减速上升,又经2秒刚好停在井口,试画出升降机的速度—时间图像,并求井深.?
第3课时 匀变速直线运动位移与时间的关系(一)
自主知识梳理
1.匀速直线运动的位移公式为________________________.
2.匀变速直线运动位移公式______________________________.
3.匀变速直线运动平均速度公式_________________________.
典型例题解析
例1:一辆沿平直公路匀速行驶的汽车,过桥后以1.0m/s2的加速度加速行驶,经12s已离开桥头180m,汽车原来匀速行驶的速度多大?
解析:过桥后,汽车以原来匀速行驶的速度为初速度,作匀加速运动,其运动示意图如图所示.已知a=1.0m/s2,t=12s,s=180m,要求初速.
根据匀加速运动位移公式
说明 解题时,应通过对题意的分析画出示意图,并标注有关物理量,这样会有助于发现其间的相互关系,迅速找到解题的入口.
例2:一辆沿平直路面行驶的汽车,速度为36km/h.刹车后获得加速度的大小是4m/s2,求:(1)刹车后3s末的速度;
(2)从开始刹车至停止,滑行一半距离时的速度.
解析:汽车刹车后作匀减速滑行,其初速度v0=36km/h=10m/s,末速度vt=0,加速度a=-4m/s2.设刹车后滑行ts停止,滑行距离为s,其运动示意图如图2-33所示.
解答 (1)由速度公式vt=v0+at得滑行时间:
即刹车后经2.5s车停止,所以3s末的速度为零.
(2)由位移公式得滑行距离,即
设滑行一半距离至B点时的速度为vB,由推论
说明 (1)不能直接把t=3s代入速度公式计算速度,因为实际滑行时间只有2.5s.求解刹车滑行一类问题,必须先确定实际的滑行时间(或位移);(2)滑行一半距离时的速度不等于滑行过程中的平均速度.
自我评价
1.作初速度为零的匀加速直线运动的物体,将其运动时间顺次分成1∶2∶3的三段,则每段时间内的位移之比为 ( )?
A.1∶3∶5 B.1∶4∶9 C.1∶8∶27 D.1∶16∶81?
2.有一个作匀加速直线运动的物体通过A点和B点时的速度分别为υA和υB.?
(1)通过AB中点C时的速度是 ( )?
A. B.
C. D.以上答案都不对?
(2)设通过AB的时间为t,则在时刻的速度为 ( )?
A. B.
C. D.以上答案都不对?
3.如图所示,完全相同的三块木块并排固定在水平面上,一颗子弹以速度υ水平射入,若子弹在木块中做匀减速直线运动,且穿过第三块木块后速度恰好为零,则子弹依次射入每块木块时的速度之比和穿过每块木块所用时间之比为 ( )?
第3题图
A.υ1∶υ2∶υ3=3∶2∶1 B.υ1∶υ2∶υ3=∶∶1?
C.t1∶t2∶t3=1∶(-1)∶(-) D.t1∶t2∶t3=(-)∶(-1)∶1
4.火车以速度υ1向前行驶,司机突然发现,在其前方同一轨道上距车为s处有另一辆火车,它正沿相同方向以较小的速度υ2做匀速运动,于是他立即使车做匀减速运动,要使两车不致相撞,后面火车的加速度应满足的条件是 .
5.某质点做匀变速直线运动,通过A点时的速度为3m/s。若从A点开始计时,第4s末的速度为11m/s,则该质点的加速度为_______m/s2,在这4s内的位移为________m,第6s初的速度为________m/s。
6.沿平直公路做匀加速直线运动的汽车经过连续三根电线杆的时间间隔分别为3s和2s,已知相邻两电线杆的距离是60m,则汽车的加速度为____________.?
7.一物体做匀变速直线运动,前4s内通过的位移为16m,第6s末的瞬时速度为8m/s,则⑴该物体的初速度和加速度各多大?⑵该物体在第7s内的位移多大?
8.一物体在与初速度相反的恒力作用下做匀变速直线运动,υ0=20m/s,加速度大小a=5m/s2.求?(1)物体经多少时间回到出发点 ?(2)物体回到出发点的速度为多大 ?(3)由开始运动算起,6s末时物体的速度.
第4课时 匀变速直线运动位移与时间的关系(二)
自主知识梳理
1.匀变速直线运动位移和速度的关系式为_________________________.
2.通过进一步的推论可得:(1)在连续相等时间内位移之差为一个___________。
(2)某段时间内中间时刻的瞬时速度________这段时间内的平均速度.(填“大于”、“等于”或“小于”)
典型例题解析
例1:矿井里的升降机,由静止开始匀加速上升,经5s速度达到4m/s后,又以这个速度匀速上升20s,然后匀减速上升,经过4s停在井口,求矿井的深度?
解析:因为升降机从井底到井口的运动分为三段,一般要分别根据匀加速、匀速、匀减速运动的规律进行计算.
1.匀加速上升时:
2.匀速上升时:h2=vt2=4×20=80(m)
3.匀减速上升时:
∴ 矿井的深度h=h1+h2+h3=10+80+8=98(m).
本题如用平均速度来解,就不用求a1、a2,而只要根据平均速度求出、,然后用来进行计算即可。
例2:一列火车进站前先关闭汽阀,让车滑行.滑行了300m时,速度恰减为关闭汽阀时的速度的一半.此后,又继续滑行了20s而停止在车站中.设火车在滑行过程中加速度始终保持不变.试求:(1)火车从关闭汽阀到停止滑行时,滑行的总路程.(2)火车滑行的加速度.(3)火车关闭汽阀时的速度.
解析:画火车运动过程的示意图,本题可把火车的匀减速运动分成二段来考查.
1.以vA的方向为正方向,设加速度为a.
由AB段的条件得:
由BC段的条件得
再把条件vA=2vB代入上式,可解得:
则火车滑行的总路程为:s=s1+s2=300+100=400(m)
2.由BC段得
故火车滑行时的加速度为
负号表示加速度方向与初速度方向相反.
3.由AC段得
故火车关闭汽阀时速度为
自我评价
1.物体做匀变速直线运动,在t时间内通过的路程为s,它在中间位置的速度为υ1,在中间时刻时的速度为υ2,则υ1和υ2的关系正确的是 ( )
A.当物体做匀加速直线运动时,υ1>υ2
B.当物体做匀减速直线运动时,υ1>υ2?
C.当物体做匀速直线运动时,υ1=υ2
D.当物体做匀减速直线运动时,υ1<υ2?
2.物体的初速度为υ0,以不变的加速度a做直线运动,如果要使速度增加到初速度的n倍,则经过的位移是( )?
A.(n2-1) B. (n-1) C.n2 D.(n-1)2?
3.物体做匀变速直线运动,它的位移与时间的关系式为s=4t+4t2,s与t的单位分别是m和s,则物体的初速度与加速度分别为 ( )
A.4m/s,4m/s2 B.4m/s,8m/s2 C.8m/s,4m/s2 D.8m/s,8m/s2
4.机车原来的速度是36km/h,在一段下坡路上得到0.2m/s2的加速度,行驶到坡底的速度为54km/h,则机车下坡所用时间为_______,这段下坡路的长度为__________m。
5.甲、乙两物体在一直线上相距为d,从某一刻起甲做速度为υ的匀速运动,乙做初速度为零,加速度为a的匀加速直线运动,乙在前,甲在后,则甲、乙能相遇一次的条件是____________,甲、乙能相遇两次的条件是____________,甲、乙不能相遇的条件是____________.?
6.火车以15m/s的速度匀速前进,现需在某站临时停车,如果在该站停留时间为1min,火车进站时的加速度大小为a1=0.3m/s2.出站时的加速度大小为a2=0.5m/s2,则火车由于在该站临时停车所延误的时间为 .
7.一辆汽车从静止开始做匀加速直线运动,已知在2s内经过相距27m的A、B两点,汽车经过B点时的速度为15m/s.求:(1)汽车经过A点时的速度大小;(2)A点与出发点间的距离;(3)汽车从出发点到A点的平均速度大小.
???
8.一辆摩托车行驶时能达到的最大速度是30米/秒.现从静止出发,并要求三分钟内追上前面100米处以20米/秒速度匀速前进的汽车,则摩托车的加速度至少为多少 ??
第5课时 自由落体运动
自主知识梳理
1._____________________________________________________________________________________________________________________________叫自由落体运动。
2.自由落体加速度的大小为____________________,方向为______________________。
3.自由落体运动的规律的速度公式为______________,位移公式为_______________。
典型例题解析
例1:从离地500m的空中自由落下一个小球,不计空气阻力,取g=10m/s2,求
(1)经过多少时间落到地面;
(2)从开始落下的时刻起,在第1s内的位移、最后1s内的位移;
(3)落下一半时间的位移.
解析:由h=500m和自由落体加速度,根据位移公式可直接算出落地时间.根据运动时间,可算出第1s内位移和落下一半时间的位移.最后1s内的位移是下落总位移和前(n-1)s下落位移之差.
(1)由,得落地时间
(2)第1s内的位移;
因为从开始运动起前9s内的位移为
所以最后1s内的位移为
h10=h-h9=500m-405m=95m.
(3)落下一半时间即t′=5s,其位移为
例2:一个物体从塔顶上下落,在到达地面前最后1s内通过的位移是整个位移的9/25,求塔高.(g取10m/s2)
解析:设物体下落总时间为t,塔高为h,则
由方程①、②解得
t=5(s)
自我评价
1.下列的那种运动可看成是自由落体运动 ( )?
A.冬季下雪时,雪花的下落
B.从桌边落下的钢笔的运动?
C.从水面自由落到水底的石子的运动
D.跳伞运动员下落的运动?
2.从某建筑物顶自由下落的物体,在落地前的1s内下落的高度为建筑物高的,则物体落到地面的瞬间速度为(g取10m/s2) ( )?
A.10m/s B.15m/s C.20m/s D.25m/s?
3.甲物体从高处自由下落一段时间后,乙物体从同一位置自由下落.若以甲为参考系,则乙物体的运动状态是(甲、乙均未着地) ( )?
A.相对静止 B.向上做匀速直线运动?
C.向下做匀速直线运动 D.向上做匀变速直线运动?
4.物体从高180m处自由下落,把它运动的总时间分成相等的三段,则这三段时间内下落的高度分别为_______m、______m和______m,物体落地时的速度为________m/s。
5.一宇航员在某星球上从高3.2m处自由释放一重物,测得在最初下落1s内所通过的距离为0.8m,则重物下落的总时间是____________,该星球的重力加速度为____________.
6.一矿井深为125m,在井口每隔一定时间自由下落一个小球.当第11个小球刚从井口开始下落,第1个小球刚好到达井底,则相邻小球开始下落的时间间隔为 s;这时第3个小球和第5个小球相距 m.(g取10m/s2)?
7.一条铁链AB长0.49米,系于A端使它竖直下垂,然后让它自由落下,求整条铁链通过悬点下2.45米处的小孔O点时需要的时间.?
8.一座高16m的建筑物屋檐处,每隔一定时间有一滴水落下,当第五滴水离开屋檐时,第一滴水正好落到地面,则此时第三滴水离开地面的高度是多少?(g取10m/s2)
第6课时 伽利略对自由落体运动的研究
自主知识梳理
1.伽利略运用了哪些方法说明了重物与轻物下落得同样快?
2.伽利略得出自由落体运动速度随时间变化的规律是怎样的
3.伽利略科学思想方法的核心是什么
典型例题解析
例1:从一定高度的气球上自由落下两个物体,第一物体下落1s后,第二物体开始下落,两物体用长93.1m的绳连接在一起.问:第二个物体下落多长时间绳被拉紧.
解析:设第二个物体下落ts后绳被拉紧,此时两物体位移差Δh=93.1m
解得 t=9(s)
例2:长5米的铁链,悬其上端。若从悬挂点放开铁链。求铁链经过悬挂点以下25米处所需的时间。
解析:铁链经过悬挂点下面25米处所需的时间,即铁链下落至A1B1到A2B2时所经历的时间(如图)。
设铁链上端A落到A1的时间为t1,落到A2的时间为t2,铁链经过悬挂点以下25米处所需时间为
秒
秒≈0.24秒。
自我评价
1.石块自高为h处的楼房顶自由落下,落地前的速度为v,当石块下落h/4距离时的速度为 ( )
A. B. C. D.
2.做自由落体运动的物体,当它落到全程的一半和全程所用的时间的比是( )?
A. B. C. D.
3.自由下落的物体,自起点开始依次下落三段相等位移所用的时间的比是( )?
A.1∶3∶5 B.1∶4∶9?
C.1∶∶ D.1∶(-1)∶(-)?
4.从塔顶释放一个小球A,1s后从同一个地点再释放一个小球B.设两球都作自由落体运动,则落地前,A、B两球之间的距离 [ ]
A.保持不变. B.不断增大.
C.不断减小. D.有时增大,有时减小.
5.利用水滴下落可以测出重力加速度g:调节水龙头,让水一滴一滴地流出.在水龙头的正下方放一个盘子,调整盘子的高度,使一个水滴碰到盘子时,恰好有一水滴从水龙头开始下落,而空中还有一个正在下落中的水滴.测出水龙头到盘子间距离h.再用秒表测时间,从第一个水滴离开水龙头开始计时,到第N个水滴落至盘中,共用时间为T.第一个水滴到盘子时,第二个水滴离开水龙头的距离是____________,重力加速度g=____________.?
6.在一条软绳两端各结一石块,拿着上端的石块使它与桥面相平,下端石块距桥面3m,放手让石块自由下落,测得两石块落水声相隔0.1s,则桥面距水面 m.(g取10m/s2
7.甲、乙两物体分别从不同高度自由落下,同时落地。已知甲物体自由落下的时间为3s,乙物体自由下落的时间为1s,那么当乙物体开始下落时甲物体距离地面的高度是多少?(g取10m/s2)
8.从离地500m的空中自由落下一个小球,不计空气阻力,取g=10m/s2,求
(1)经过多少时间落到地面;
(2)从开始落下的时刻起,在第1s内的位移、最后1s内的位移;
(3)落下一半时间的位移.
A卷 单元评估
1.一物体从斜面上某点由静止开始作匀加速直线运动,经过3s后到达斜面底端并开始在水平地面上作匀减速直线运动,又经9s停止,则物体在斜面上的位移与水平地面上的位移之比是( )?
A.1∶1 B.1∶2 C.1∶3 D.3∶1?
2.质点作直线运动的v-t图线如图所示,初速度为v0,末速度为v1,则时间t1内的平均速度为
A.
B.
C.
D.无法比较
3.作匀加速直线运动的列车出站时,车头经过站台时的速度为1m/s,车尾经过站台时的速度为7m/s,则列车中部经过站台时的速度为
A.3.5m/s B.4.0m/s C.5.0m/s D.5.5m/s
4.一辆汽车以72km/h的速度沿平直公路匀速前进,司机发现前方有障碍物,立即紧急制动,汽车以5m/s2加速度做匀减速运动,则汽车在制动以后2s内与制动以后6s内的内移之比是( )?
A.1∶1 B.3∶4 C.3∶1 D.4∶3?
5.对做匀加速直线运动的物体,下列说法中正确的是( )?
A.在第1s内、第2s内、第3s内的位移之比一定等于1∶3∶5
B.它的加速度是均匀增加的
C.在相同时间间隔内,它的速度变化量相同
D.在任意两个连续相等时间间隔内通过的位移之差相等
6.甲、乙两车沿平直公路从同一地点同时同向驶向同一目的地,甲车在前一半时间内以速度υ1作匀速运动,后一半时间内以速度υ2作匀速运动,乙车在前一半路程中以υ2作匀速运动,后一半路程中以速度υ1作匀速运动,下面判断中正确的是( )?
A.如果υ1大于υ2,甲车先到达目的地?
B.如果υ1大于υ2,乙车先到达目的地?
C.如果υ1小于υ2,甲车先到达目的地?
D.如果υ1小于υ2,乙车先到达目的地?
7.物体自楼顶处自由落下(不计空气阻力),落到地面的速度为υ.在此过程中,物体从楼顶落到楼高一半处所经历的时间为( )?
A.υ/2 B.υ/(2g) C.υ/(2g) D.2-υ/(2g)
8.足够长的平直的公路上,一辆汽车以a起动时,有一辆匀速行驶的自行车以速度v0从旁驶过,则 ( )
A.汽车追不上自行车,因为汽车起动时速度小
B.以汽车为参考系,自行车是向前作匀减速直线运动
C.汽车与自行车之间的距离开始是不断增加的,直至两者速度相等,然后两者间的距离逐渐减小,直至两车相遇
D.汽车追上自行车的时间是2 v0/a
9.一根木棍保持竖直状态静止不动,在木棍正下方距木棍上端0.8m处有一点A,当木棍由静止释放后,木棍通过A点所用时间是0.2s,不计空气阻力,g取10m/s2,则可知木棍的长度是_______m。
10.在“测定匀变速直线运动的加速度”的实验中,用打点计时器记录纸带运动的时间.计时器所用电源的频率为50Hz,图Ⅱ-4为一次实验得到的一条纸带,纸带上每相邻的两计数点间都有四个点未画出,按时间顺序取0、1、2、3、4、5六个计数点,用米尺量出1、2、3、4、5点到O点的距离如图所示(单位:cm)。由纸带数据计算可得计数点4所代表时刻的瞬时速度大小υ4=__________m/s,小车的加速度大小a=__________m/s2.
第13题图
11.火车正以108km/h的正常速度行驶着,因前方出现意外而临时停车。停车前火车作加速度大小为1m/s2的匀减速运动,1min30s后停止,停止1min后,又以0.5m/s2的加速度起动,作匀加速直线运动,直至速度恢复正常为止。求因临时停车而延误的时间。
12.甲、乙两个物体同时经过某路口向同方向做直线运动,甲以4米/秒的速度做匀速运动,乙从此路口由静止开始以2米/秒2的加速度做匀加速直线运动,问从他们经过路口开始计时多长时间后,他们第一次又相遇,相遇时距路口多远 在相遇前两物体何时距离最大 最大距离是多少 ???????
B卷 单元评估
1.关于质点的位移和路程,下列说法中正确的是( )
A.位移是矢量,位移的方向即质点运动的方向
B.位移的大小不会比路程大
C.路程是标量,即位移的大小
D.当质点作直线运动时,路程等于位移的大小
2.质点以2m/s2的加速度作匀加速运动,下列说法中正确的是( )
A.质点的加速度越来越大
B.质点的速度每经1s增加2m/s
C.质点在任1s内位移比前1s内大2m
D.质点在任1s内的平均速度比前1s内的平均速度大2m/s
3.一物体从斜面顶端由静止开始下滑,经过ts到达斜面中点,此时的速度为υ,则该物体到达斜面底部的时间和速度分别是( )?
A.t, υ B.2t,2υ C. t,2t D.2t, υ?
4.下列运动形式可能的是( )
A.物体的速度很大,但加速度为零
B.物体的速度为零,但加速度很大
C.物体的加速度减小,速度一定减小
D.物体的加速度增大,但速度减小
5.一枚火箭由地面竖直向上发射,其速度如下图所示,则 ( )?
第6题图
A.在B时刻火箭达到最大高度?
B.在C时刻火箭落回地面?
C.在BC段火箭加速度最大
D.在AB段火箭加速度最大?
6.甲、乙、丙三辆汽车以相同的速度v经过同一位置A,随后,甲一直做匀速运动,乙先加速后减速,丙先减速后加速,当它们经过下一个相同位置B时,又具有了相同的速度且仍为v,则( )
A.甲车先通过B点 B.乙车先通过B点
C.甲车最后通过B点 D.丙车最后通过B点
7.如图所示为某郊区部分道路图,一歹徒在A地作案后乘车沿AD道路逃窜,警方同时接到报警信息,并立即由B地乘警车沿道路BE拦截,歹徒到达D点后沿DE道路逃窜,警车恰好在E点追上了歹徒,已知警方与歹徒车辆行驶的速度均为60km/h,AC=4km,BC=6km,DE=5km,则歹徒从A地逃窜至E点被抓获共用时 ( )?
第8题图
A.12min B.10min C.8min D.6min?
8.从某一高度h1处自由落下一物体A,1s后从另一较低高度h2处自由落下另一物体B。若A自由下落45m时赶上B,并再经1s落地,则B从下落到落地共经历的时间约为(g取10m/s2) ( )
A.3s B.3.3s C.3.5s D.4s
9.以12m/s的速度在平直公路上匀速行驶的公共汽车,在距某站牌32m处开始制动,作匀减速直线运动,若加速度大小为2m/s2,行车的方向末变,则它由开始制动到通过站牌所用的时间为________s。(不计汽车的长度)
10.用打点计时器研究匀变速直线运动的规律的实验中,得到一段纸带如图2-42所示,O点为起始点,取A为第一个计数点,以后每5个连续点取为一计数点。则
①打点计时器的连续打两个点的时间间隔为______s,相邻两个计数点的时间间隔为________s;
②若量得OA=4.82cm,OB=6.74cm,OC=8.04cm,OD=9.80cm,OE=12.02cm,则这个运动可能是_________运动,其加速度大小为_____m/s2,B点的速度大小为________m/s,C点的速度大小为_________m/s。
11.某飞机起飞滑行时,从静止开始做匀加速直线运动,加速度大小为4.0m/s2,飞机速度达到80m/s时将离开地面升空。如果在飞机达到起飞速度时,突然接到命令停止起飞,飞行员立即使飞机紧急制动,作匀减速直线运动,加速度的大小为5m/s2。则该飞机场起飞跑道的长度至少多长?
12.一物体从固定斜面的顶端由静止开始匀加速沿斜面下滑,已知物体在斜面上滑行的最初3s通过的路程为s1,物体在斜面上滑行的最后3s,通过的路程为s2,且s2-s1=6m,已知s1∶s2=3∶7,求斜面的长度?
第二章 匀变速直线运动的研究
参考答案与提示
第1课时 实验:探究小车速度随时间变化的规律
自主知识梳理
1.打点计时器;纸带,复写纸片;低压交流电源;小车;细绳;一端附有滑轮的长木板;刻度尺;钩码;两根导线。
2.运用平均速度公式,当较小时即可代表瞬时速度。
3.一条倾斜的直线:速度随时间均匀地增加。
自我评价
1. ACD.
2.ABD
3.B
4.C
5. (1)C (2)33
6.1.86 0.972
7.BFCADE
第2课时 匀变速直线运动速度与时间的关系
自主知识梳理
1.沿着一条直线,且加速度保持不变的运动叫做匀变速直线运动.
2.
3.一条倾斜的直线.
4.对应关系,斜率越大加速度越大.
自我评价
1.D
2.C
3.ABC
4.3m/s2;向东;0;1.5m/s2;向西;
5.初速度为零的匀加速直线运动匀减速直线运动;小于;相反?
6.360m/s2,方向竖直向上?
7. 。
8. 速度—时间图像;井深为25.5米。
第3课时 匀变速直线运动位移与时间的关系(一)
自主知识梳理
1. .
2.
3.
自我评价
1.C
2.(1)C;(2)A
3.D
4.a≥
5.2;28;13
6.4m/s2
7.(1)v0=2m/s a=1m/s2 ⑵
8.(1)8s;(2)20m/s;(3)10m/s与υ0方向相反
第4课时 匀变速直线运动位移与时间的关系(二)
自主知识梳理
1.
2.(1)恒量(2)等于
自我评价
1. ABC
2.A
3.B
4.25s;312.5
5.υ2=2ad;υ2>2ad;υ2<2ad
6.100s?
7.(1)12m/s;(2)48m;(3)6m/s?
8. m/s2??
第6课时 伽利略对自由落体运动的研究
自主知识梳理
1.逻辑推理和实验验证
2.自由落体运动速度随时间是均匀变化的。
3.把实验与逻辑推理和谐地结合起来。
自我评价
1.C
2.C
3.D
4.B
5.;
6.46.51m?
7.(m)
8.(1)10s (2)5m 95m. (3) 125m
A卷 单元评估
1.C
2.B
3.C
4.B
5.CD
6.AC
7.C?
8.BCD
9. 0.6
10.0.405m/s;0.76m/s2?
11.195s
12.4s,16m;2s,4m
B卷 单元评估
1.B
2.BCD
3.A
4.ABD
5.C
6.BD
7.B
8.B
9.4s
10.①0.02;0.1;②匀加速直线;0.46;0.107;0.153
11.1440m
12.12.5m
第3题图
第14题图
课件中心精品资料 www. 版权所有@课件中心 第 19 页 共 19 页
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
