高中物理解题方法--隔离法[上下学期通用]
文档属性
| 名称 | 高中物理解题方法--隔离法[上下学期通用] |

|
|
| 格式 | rar | ||
| 文件大小 | 620.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2006-11-11 00:00:00 | ||
图片预览



文档简介
课件中心精品资料 www. 找精品资料 到课件中心
高中物理解题方法——隔离法
方法简介
隔离法就是从整个系统中将某一部分物体隔离出来,然后单独分析被隔离部分的受力情况和运动情况,从而把复杂的问题转化为简单的一个个小问题求解。隔离法在求解物理问题时,是一种非常重要的方法,学好隔离法,对分析物理现象、物理规律大有益处。
例1:两个质量相同的物体1和2紧靠在一起放在光滑水平
桌面上,如图2—1所示,如果它们分别受到水平推
力F1和F2作用,且F1>F2, 则物体1施于物体2的
作用力的大小为 ( )
A.F1 B.F2 C.1/2(F1+F2) D.1/2(F1-F2)
解析:要求物体1和2之间的作用力,必须把其中一个隔离出来分析。
先以整体为研究对象,根据牛顿第二定律:F1-F2=2ma ①
再以物体2为研究对象,有N-F2=ma ②
解①、②两式可得所以应选C
例2:如图2—2在光滑的水平桌面上放一物体A,A上再放一物体B,
A、B间有摩擦。施加一水平力F于B,使它相对于桌面向右运
运,这时物体A相对于桌面 ( )
A.向左动 B.向右动
C.不动 D.运动,但运动方向不能判断
解析:A的运动有两种可能,可根据隔离法分析
设AB一起运动,则
AB之间的最大静摩擦力
以A为研究对象:若一起向右运动.
若则A向右运动,但比B要慢,所以应选B
例3:如图2—3所示,已知物块A、B的质量分别为m1、m2,A、B间的摩擦因数为μ1,A与地面之间的摩擦因数为μ2,在水平力F的推动下,要使A、B一起运动而B不至下滑,力F至少为多大?
解析: B受到A向前的压力N,要想B
不下滑,需满足的临界条件是:μ1N=m2g.
设B不下滑时,A、B的加速度为a,以B为研究对象,用隔离法分析,B受到重力,A对B的摩擦力、A对B向前的压力N,如图2—3甲所示,要想B不下滑,需满足:μ1N≥m2g,即:μ1m2a≥m2g,所以加速度至少为a=g/μ1
再用整体法研究A、B,根据牛顿第二定律,有:F—μ2(m1+m2)g=(m1+m2)g=(m1+m2)a,所以推力至少为.
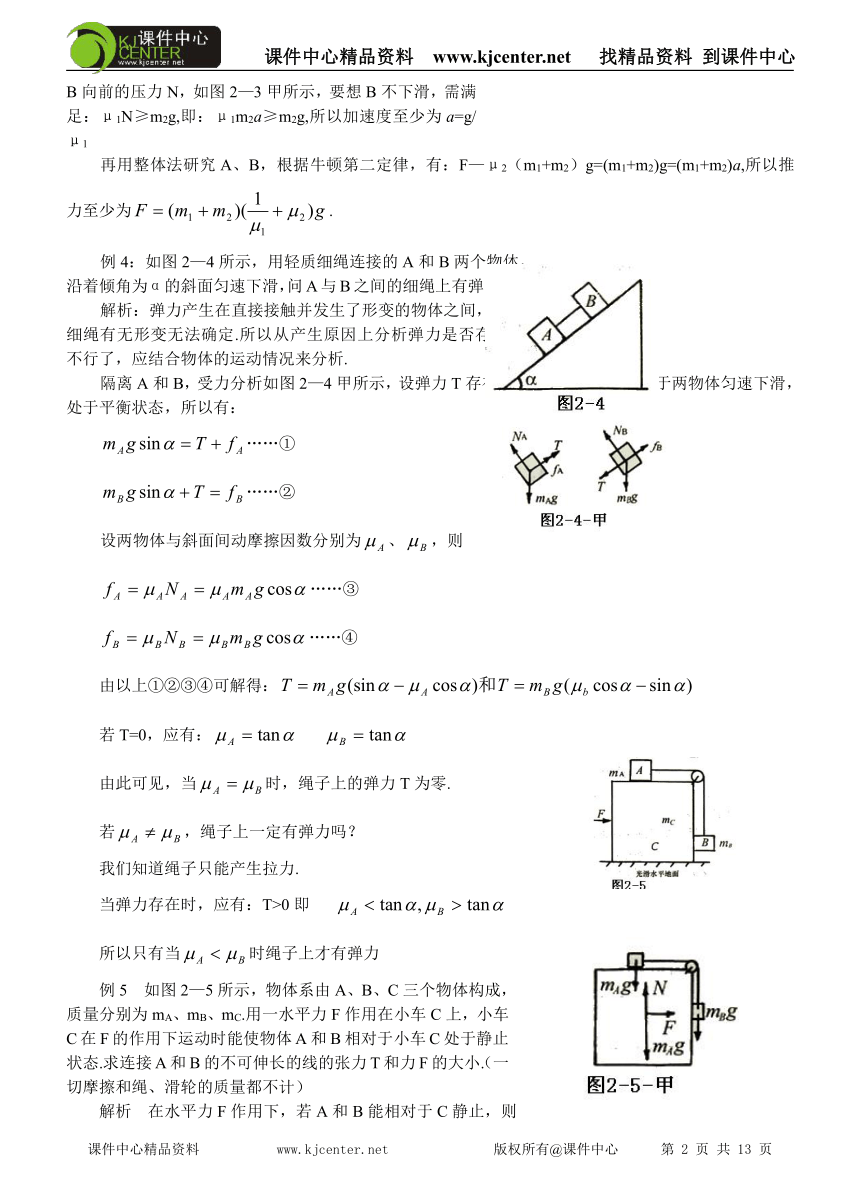
例4:如图2—4所示,用轻质细绳连接的A和B两个物体,沿着倾角为α的斜面匀速下滑,问A与B之间的细绳上有弹力吗?
解析:弹力产生在直接接触并发生了形变的物体之间,现在细绳有无形变无法确定.所以从产生原因上分析弹力是否存在就不行了,应结合物体的运动情况来分析.
隔离A和B,受力分析如图2—4甲所示,设弹力T存在,将各力正交分解,由于两物体匀速下滑,处于平衡状态,所以有:
……①
……②
设两物体与斜面间动摩擦因数分别为、,则
……③
……④
由以上①②③④可解得:
若T=0,应有:
由此可见,当时,绳子上的弹力T为零.
若,绳子上一定有弹力吗?
我们知道绳子只能产生拉力.
当弹力存在时,应有:T>0即
所以只有当时绳子上才有弹力
例5 如图2—5所示,物体系由A、B、C三个物体构成,质量分别为mA、mB、mC.用一水平力F作用在小车C上,小车C在F的作用下运动时能使物体A和B相对于小车C处于静止状态.求连接A和B的不可伸长的线的张力T和力F的大小.(一切摩擦和绳、滑轮的质量都不计)
解析 在水平力F作用下,若A和B能相对于C静止,则它们对地必有相同的水平加速度.而A在绳的张力作用下只能产生水平向右的加速度,这就决定了F只能水平向右,可用整体法来求,而求张力必须用隔离法.
取物体系为研究对象,以地为参考系,受重力(mA+mB+mC)g,推力F和地面的弹力N,如图2—5甲所示,设对地的加速度为a,则有:
…………①
隔离B,以地为参考系,受重力mBg、张力T、C对B的弹力NB,应满足:
…………②
隔离A,以地为参考系,受重力mAg,绳的张力T,C的弹力NA,应满足;
NA=mAg…………③
T=mAa…………④
当绳和滑轮的质量以及摩擦都不计时,由②、④两式解出加速度
代入①式可得:
例6 如图2—6所示,一根轻质弹簧上端固定,下端挂一质量为m0的平盘,盘中有一物体质量为m,当盘静止时,弹簧的长度比其自然长度伸长了L,今向下拉盘,使弹簧再伸长△L后停止.然后松手放开,设弹簧总处在弹性限度以内,则刚松开手时盘对物体的支持力等于( )
A. B.
C. D.
解析 确定物体m的加速度可用整体法,确定盘对物体的支持力需用隔离法.选整体为研究对象,在没有向下拉盘时有
KL=(m+m0)g…………①
在向下拉伸△L又放手时有
K△L=(m+m0)a……②
再选m为研究对象 FN-mg=ma……③
解得:
应选A.此题也可用假设法、极限法求解.
例7 如图2—7所示,AO是质量为m的均匀细杆,可绕O轴在竖直平面内自动转动.细杆上的P点与放在水平桌面上的圆柱体接触,圆柱体靠在竖直的挡板上而保持平衡,已知杆的倾角为θ,AP长度是杆长的1/4,各处的摩擦都不计,则挡板对圆柱体的作用力等于 。
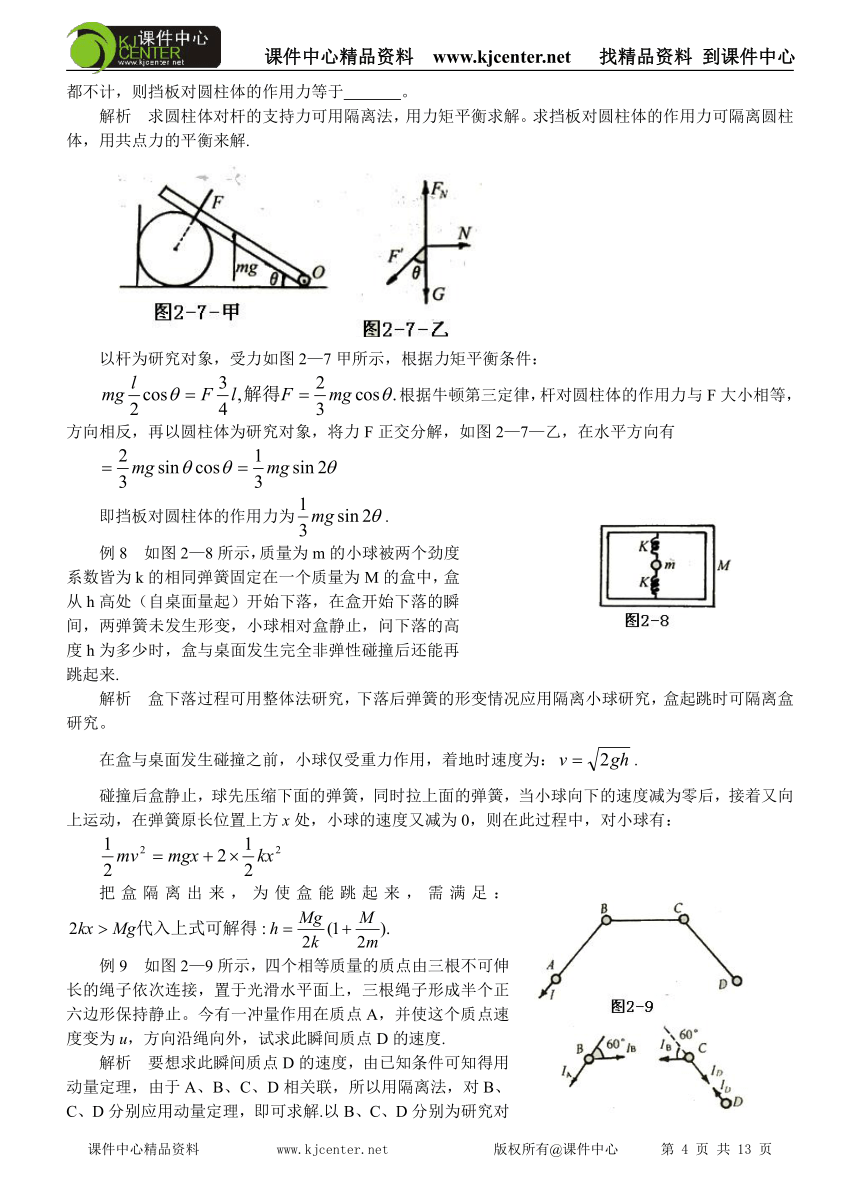
解析 求圆柱体对杆的支持力可用隔离法,用力矩平衡求解。求挡板对圆柱体的作用力可隔离圆柱体,用共点力的平衡来解.
以杆为研究对象,受力如图2—7甲所示,根据力矩平衡条件:
根据牛顿第三定律,杆对圆柱体的作用力与F大小相等,方向相反,再以圆柱体为研究对象,将力F正交分解,如图2—7—乙,在水平方向有
即挡板对圆柱体的作用力为.
例8 如图2—8所示,质量为m的小球被两个劲度系数皆为k的相同弹簧固定在一个质量为M的盒中,盒从h高处(自桌面量起)开始下落,在盒开始下落的瞬间,两弹簧未发生形变,小球相对盒静止,问下落的高度h为多少时,盒与桌面发生完全非弹性碰撞后还能再跳起来.
解析 盒下落过程可用整体法研究,下落后弹簧的形变情况应用隔离小球研究,盒起跳时可隔离盒研究。
在盒与桌面发生碰撞之前,小球仅受重力作用,着地时速度为:.
碰撞后盒静止,球先压缩下面的弹簧,同时拉上面的弹簧,当小球向下的速度减为零后,接着又向上运动,在弹簧原长位置上方x处,小球的速度又减为0,则在此过程中,对小球有:
把盒隔离出来,为使盒能跳起来,需满足:
例9 如图2—9所示,四个相等质量的质点由三根不可伸长的绳子依次连接,置于光滑水平面上,三根绳子形成半个正六边形保持静止。今有一冲量作用在质点A,并使这个质点速度变为u,方向沿绳向外,试求此瞬间质点D的速度.
解析 要想求此瞬间质点D的速度,由已知条件可知得用动量定理,由于A、B、C、D相关联,所以用隔离法,对B、C、D分别应用动量定理,即可求解.以B、C、D分别为研究对象,根据动量定理:
对B有:IA—IBcos60°=mBu…………①
IA cos60°—IB=mBu1…………②
对C有:IB—ID cos60°=mCu1……③
IBcos60°—ID=mcu2…………④
对D有:ID=mDu2……⑤
由①~⑤式解得D的速度
例10 有一个两端开口、粗细均匀的U形玻璃细管,放置在竖直平面内,处在压强为p0的大气中,两个竖直支管的高度均为h,水平管的长度为2h,玻璃细管的半径为r,r<1.如将U形管两个竖直支管的开口分别密封起来,使其管内空气压强均等于大气压强,问当U形管向右做匀加速移动时,加速度应为多大时才能使水平管内水银柱的长度稳定为(5/3)h?
2.如将其中一个竖直支管的开口密封起来,使其管内气体压强为1个大气压.问当U形管绕以另一个竖直支管(开口的)为轴做匀速转动时,转数n应为多大才能使水平管内水银柱的长度稳定为(5/3)h(U形管做以上运动时,均不考虑管内水银液面的倾斜)
解析 如图2—10—甲所示,U形管右加速运动时,管内水银柱也要以同样加速度运动,所以A管内气体体积减小、压强增大,B管内气体体积增大、压强减小,水平管中液体在水平方向受力不平衡即产生加速度.若U形管以A管为轴匀速转动时,水平部分的液体也要受到水平方向的压力差而产生向心加速度.
1.当U形管以加速度a向右运动时,对水平管中水银柱有F1—F2=ma
即……①
……②
……③ 2—10—乙
将②、③式代入①式可得
2.如图2—10—乙,若U形管以A管为轴匀速转动时,对水平管中水银柱有F2—F1=ma.若转轴为n,则有:
……①
对B中气体有解得:……②
将②式代入①式可解得转速
例11 如图2—11所示,一个上下都与大气相通的竖直圆筒,内部横截面的面积S=0.01m2,中间用两个活塞A与B封住一定质量的理想气体,A、B都可沿圆筒无摩擦地上、下滑动,但不漏气,A的质量可不计,B的质量为M,并与一倔强系数k=5×103N/m的较长的弹簧相连.已知大气压强p0=1×105Pa,平衡时,两活塞间的距离l0=0.6m.现用力压A使之缓慢向下移动一定距离后,保持平衡,此时,用于压A的力F=5×102N.求活塞A向下移动的距离.(假定气体温度保持不变.)
解析 活塞A下移的距离应为B下降的距离与气体长度的减小量之和,B下降的距离可用整体法求解.气体长度的变化可隔离气体来求解.
选A、B活塞及气体为研究对象,设用力F向下压A时,活塞B下降的距离为x,
则有:F=kx…………①
选气体为研究对象,据玻意耳定律有…………②
解①②两式可得x=0.1m l=0.4m则活塞A下移的距离为:左=0.1+0.6—0.4=0.3m
例12 一个密闭的气缸,被活塞分成体积相等的左右两室,气缸壁与活塞是不导热的,它们之间没有摩擦,两室中气体的温度相等,如图2—12所示,现利用右室中的电热丝对右室中的气体加热一段时间,达到平衡后,左室的体积变为原来体积的3/4,气体的温度T1=300K.求右室中气体的温度.
解析 可隔离出A、B两部分气体,用理想气体状态方程求解.
设原来两室中气体的压强都为p,温度都为T,体积都为V,
对左边气体有……①对右边气体有②
①、②两式相比,可得右室中气体温度
例13 如图2—13所示,封闭气缸的活塞被很细的弹簧拉着,气缸内密封一定质量的气体,当温度为27℃时,弹簧的长度为30cm,此时缸内气体的压强为缸外大气压的1.2倍,当气温升到123℃时,弹簧的长度为36cm,求弹簧的原长.
解析 本题所研究的对象就是密封在气缸内的一定质量的气体,气体所处的初态为:
T1=300K、V1=SL1、(S为气缸横截面积,L1为弹簧长度)p1=p0+F1/S=1.2P0末态为T2=396K、V2=SL2 p2=p0+F2/S(p0为大气压强,F1、F2为弹簧的弹力).气体从初态过渡到末态时质量恒定,所以可利用状态方程求解:
将上述各状态参量代入状态方程:
解得:由于弹力产生的压强等于气缸内外气体的压强差,
所以: ①
②
联立①、②式得:
解得弹簧的原长为L0=20cm
例14 一个由绝缘细细构成的钢性圆形轨道,其半径为R,此轨道水平放置,圆心在O点,一个金属小珠P穿在此轨道上,可沿轨道无摩擦地滑动,小珠P带电荷Q.已知在轨道平面内A点(OA=r解析 小珠P虽沿轨道做匀速圆周运动,但受力情况并不清楚,因此不能从力的角度来解决,可以从电势的角度来考虑,因为小珠P沿轨道做匀速圆周运动,说明小珠只受法向的电场力.由此可知,电场力对小珠P做功为零,根据W=qU可知,圆轨道上各点电势相等,根据题意作图如图2—14,设A1点距圆形轨道的圆心O为r1,A点放的电荷q距圆心为r
由此得:
解①、②两式可得:A1点的位置距圆心O的距离为,所带电量
例15 如图2—15所示,两个电池组的电动势每节电池的内阻均为0.5Ω,R1=1Ω,R2=2Ω,R3=1.8Ω,求通过R1、R2、R3的电流及两个电池组的端电压各是多少?
解析 解此题时,可采用与力学隔离法相似
的解法,即采用电路隔离法.
气体从初态过渡到末态时质量恒定,所以可利用状态方程求解.
先将整个电路按虚线划分为Ⅰ、Ⅱ、Ⅲ三个部分,则有:
UAB=ε1—I1(R1+2r)……①
UAB=ε2—I2(R2+2r)………………②
UAB=I3R3……………………③
I1+I2=I3………………④
联立①②③④四式解得:I1=0.6A,I2=0.4A,I3=1A,电池组ε的端电压U1=2.4V,电池组ε2的端电压U2=2.6V.
例16 如图2—16所示,两根相互平行的间距L=0.4m的金属导轨水平放在B=0.2T的匀强磁场中,磁场垂直于导轨平面,导轨上的滑杆ab、cd所受摩擦力均为0.2N,两杆电阻均为0.1Ω,导轨电阻不计.当ab受到恒力F作用时,ab以v1做匀速运动,cd以v2做匀速运动,求通过ab杆的电流强度的大小和方向.
解析 要求通过ab杆的电流强度,应通过ab杆受的安培力求解,这就需要隔离出ab杆进行受力分析.
以ab杆为研究对象,因右手定则确定电流的方向为b→a,受力如图2—6—甲所示.因为ab杆匀速运动处于平衡状态,故有
F=f+BIL.
再以滑杆ab、cd整体作为研究对象,受力如图2—16—乙所示,因为ab、cd均做匀速运动,受力平衡,故有
代入上式,解得通过ab杆的电流为
所以通过ab杆的电流的大小为2.5A,方向b→a.
针对训练
1.质量为8kg的木块m放在质量为16kg的木板M上,并通过滑轮用细绳连接,如图2—17所示,M与m间,M与水平地面间的动摩擦因数μ均为0.25,滑轮摩擦不计.欲使M向匀速运动,水平拉力应为多大?(g取10m/s2)
2.在水平面上有两个物体A和B,它们之间用不可伸缩的质量不计的细绳连接起来,其中mA=3kg,mB=2kg,它们与地面间的动摩擦因数μ=0.1.如图2—18所示,今用一与水平方向成37°角、大小为10N的恒力拉B,使AB一起向右做匀加速直线运动,试求A对B的拉力.(g取10m/s2)
3.如图2—19所示,小物体m放在大物体M上,M系在固定于墙上的水平弹簧的另一端,并置于光滑水平面上,若弹簧的劲度系数为k,将M向右拉离平衡位置x后无初速度释放,在以后的运动中M与m保持相对静止,那么m在运动中受到的最大和最小摩擦力分别为多大?
4.电梯内有一个物体,质量为m,用细线挂在电梯的天花板上,当电梯以g/3的加速度竖直加速度竖直加速下降时(g为重力加速度),细线对物体的拉力为( )
A.2/3mg B.1/3mg C.4/3mg D.mg
5.两物体A和B,质量分别为m1和m2,互相接触放在光滑水平面上,如图2—20所示,对物体A施以水平的推力F,则物体A对物体B的作用力等于( )
A.m1F/(m1+m2) B.m2F/(m1+m2)
C.F D.m2/m1F
6.在光滑水平面上有一木板,一木棒A、B可沿水平轴O转动,其下端B搁在木板下,而整个系统处于静止状态(如图2—21所示).现在用水平力F向左推木板,但木板仍未动.由此可以得出结论:施力F后,木板和木棒之间的正压力( )
A.变大 B.不变
C.变小 D.条件不足,不能判断如何改变
7.如图2—22所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面木块压在上面的弹簧上(但不拴接),整个系统处于平衡状态.现缓慢向上提上面的木块,直到它刚离开上面弹簧,在这过程中下面木块移动的距离为( )
A.m1g/k1 B.m2g/k1
C.m1g/k2 D.m2g/k2
8.如图2—23,质量为2m的物块A与水平地面的摩擦可忽略不计,质量为m的物块B与地面的摩擦系数为μ.在已知水平推力F的作用下,AB做加速运动,A对B的作用力为 .
9.如图2—24所示,两块木块A和B,质量分别为mA和mB,紧挨着并排在水平桌面上,AB间的接触面垂直于图中纸面且与水平面成θ角。A、B间的接触面是光滑的,但它们与水平桌面间有摩擦,静摩擦系数和滑动摩擦系数均为μ.开始时A、B都静止,现施一水平推力F于A.要使A、B向右加速运动且A、B之间不发生相对滑动,则
(1)μ的数值应满足什么条件?
(2)推力F的最大值不能超过多少?
(只考虑平动,不考虑转动问题)
10.系统如图2—25所示,滑轮与绳的质量忽略,绳不可伸长。设系统所有部位都没有摩擦,物体B借助导轨(图中未画出来)被限定沿物体C的右侧面运动,试求物体C的运动加速度。
11.质量分别为m1、m2和m3的三个质点A、B、C位于光滑的水平桌面上,用已拉直的不可伸长的柔软的轻绳AB和BC连接,角ABC为为一锐角,如图2—26所示,今有一冲量为I的冲击力沿BC方向作用于质点C,求质点A开始运动时的速度.
12.如图2—27所示,四个质量均为m的质点,用同样长度且不可伸长的轻绳连结成菱形ABCD,静止放在水平光滑的桌面上.若突然给质点A一个力时极短沿CA方向的冲击,当冲击结束的时刻,质点A的速度为V,其他质点也获得一定的速度,.求此质点系统受到冲击后所具有的总动量和总能量.
13.如图2—28所示,一三角木块ABC置于光滑水平面上,两斜边与平面夹角分别为30°、60°.在斜边上有两个物体m1、m2,用不可伸长的细绳连接并跨在顶点A的定滑轮上,m1、m2可在斜面上无摩擦地滑动.已知木块的质量为M,三物体的质量比为m1:m2:M=4:1:16,滑轮光滑且质量可忽略.
(1)求M的加速度a及m1相对于M的加速度a′
(2)若m1从静止开始沿斜面移动20cm,求M沿水平面移动的距离.
14.如图2—29所示,可沿气缸壁自由活动的活塞将密封的圆筒形气缸分隔成A、B两部分.活塞与气缸顶部有一弹簧相连.当活塞位于气缸底部时弹簧恰好无形变,开始时B内充有一定量的气体,A内是真空,B部分高度为l1=0.10米,此时活塞受到的弹簧作用力与重力的大小相等.现将整个装置倒置.达到新的平衡后B部分的高度L2于多少?设温度不变.
15.图2—30中竖直圆筒是固定不动的,粗筒横截面积是细筒的4倍,细筒足够长.粗筒中A、B两轻质活塞间封有空气,气柱长l=20厘米.活塞A上方的水银深H=10厘米,两活塞与筒壁间的摩擦不计.用外力向上托住活塞B,使之处于平衡状态,水银面与粗筒上端相平.现使活塞B缓慢上移,直至水银的一半被推入细筒中,求活塞B上移的距离(设在整个过程中气柱的温度不变,大气压强p0相当于75厘米高的水银柱产生的压强).
16.如图2—31是容器的截面图,它是由A、B两部分构成,两部分都是圆筒形,高度都是h,底面积SB=S,SA=2S,容器下端有一小孔a与大气相通,上端开口,B中有一质量为m厚度不计的活塞,它与B的器壁有摩擦,最大摩擦力为f(f)mg,开始时活塞N位于B的最下端,已知大气压强为p0,当时温度为T0,现把a孔封闭,为保证封闭气体不与外界相通,筒中气体温度允许在多大范围内变化?
17.如图2—32所示,长为2l的圆形筒形气缸可沿摩擦因数为μ的水平面滑动,在气缸中央有一个截面积为S的活塞,气缸内气体的温度为T0,压强为p0(大气压强也为p0).在墙壁与活塞之间装有劲度系数为k的弹簧,当活塞处于如图位置时,弹簧恰好在原长位置.今使气缸内气体体积增加一倍,问气体的温度应达到多少?(气缸内壁光滑,活塞和气缸总质量为m).
18.A、B两带电小球,A固定不动,B的质量为m.在库仑作用下,B由静止开始运动.已知初始时A、B间的距离为d,B的加速度为a。经过一段时间后,B的加速度变为a/4,此时A、B间的距离应为 .已知此时B的速度为v,则在此过程中电势能的减少量为 .
19.如图2—33所示,是电磁流量计的示意图,在非磁性材料做成的圆管道外加一匀强磁场区域,当管中的导电液体流过磁场区域时,测出管壁上、下表面两点a、b间的电动势为ε,从而可求出管中液体在单位时间内的流量Q.已知圆管的内径为D,磁感应强度为B,试推导出Q与ε的关系表达式.
20.如图2—34所示,一矩形管中(管长为l,两侧面为导电面,并有导线在外面与之相连,上下面则为绝缘面)有电阻率为ρ的水银流动,当其一端加上压强p时,水银的流速为v0.现在竖直方向加上磁感应强度为B的匀强磁场.试证明:此时水银的流速为
.(设水银的速度与压强成正比)
答案:
1.F=100N 2.T=5.16N 3. 4.A 5.B 6.C 7.C
8. 9.(1) (2)F
10.
11.方向沿AB方向
12.P= E=
13.(1) (2) 3.78cm
14.0.2m 15.8cm 16.
17.摩擦力足够大时 摩擦力不是足够大时
18. 19. 20.证明略
EMBED Word.Picture.8
课件中心精品资料 www. 版权所有@课件中心 第 1 页 共 13 页
高中物理解题方法——隔离法
方法简介
隔离法就是从整个系统中将某一部分物体隔离出来,然后单独分析被隔离部分的受力情况和运动情况,从而把复杂的问题转化为简单的一个个小问题求解。隔离法在求解物理问题时,是一种非常重要的方法,学好隔离法,对分析物理现象、物理规律大有益处。
例1:两个质量相同的物体1和2紧靠在一起放在光滑水平
桌面上,如图2—1所示,如果它们分别受到水平推
力F1和F2作用,且F1>F2, 则物体1施于物体2的
作用力的大小为 ( )
A.F1 B.F2 C.1/2(F1+F2) D.1/2(F1-F2)
解析:要求物体1和2之间的作用力,必须把其中一个隔离出来分析。
先以整体为研究对象,根据牛顿第二定律:F1-F2=2ma ①
再以物体2为研究对象,有N-F2=ma ②
解①、②两式可得所以应选C
例2:如图2—2在光滑的水平桌面上放一物体A,A上再放一物体B,
A、B间有摩擦。施加一水平力F于B,使它相对于桌面向右运
运,这时物体A相对于桌面 ( )
A.向左动 B.向右动
C.不动 D.运动,但运动方向不能判断
解析:A的运动有两种可能,可根据隔离法分析
设AB一起运动,则
AB之间的最大静摩擦力
以A为研究对象:若一起向右运动.
若则A向右运动,但比B要慢,所以应选B
例3:如图2—3所示,已知物块A、B的质量分别为m1、m2,A、B间的摩擦因数为μ1,A与地面之间的摩擦因数为μ2,在水平力F的推动下,要使A、B一起运动而B不至下滑,力F至少为多大?
解析: B受到A向前的压力N,要想B
不下滑,需满足的临界条件是:μ1N=m2g.
设B不下滑时,A、B的加速度为a,以B为研究对象,用隔离法分析,B受到重力,A对B的摩擦力、A对B向前的压力N,如图2—3甲所示,要想B不下滑,需满足:μ1N≥m2g,即:μ1m2a≥m2g,所以加速度至少为a=g/μ1
再用整体法研究A、B,根据牛顿第二定律,有:F—μ2(m1+m2)g=(m1+m2)g=(m1+m2)a,所以推力至少为.
例4:如图2—4所示,用轻质细绳连接的A和B两个物体,沿着倾角为α的斜面匀速下滑,问A与B之间的细绳上有弹力吗?
解析:弹力产生在直接接触并发生了形变的物体之间,现在细绳有无形变无法确定.所以从产生原因上分析弹力是否存在就不行了,应结合物体的运动情况来分析.
隔离A和B,受力分析如图2—4甲所示,设弹力T存在,将各力正交分解,由于两物体匀速下滑,处于平衡状态,所以有:
……①
……②
设两物体与斜面间动摩擦因数分别为、,则
……③
……④
由以上①②③④可解得:
若T=0,应有:
由此可见,当时,绳子上的弹力T为零.
若,绳子上一定有弹力吗?
我们知道绳子只能产生拉力.
当弹力存在时,应有:T>0即
所以只有当时绳子上才有弹力
例5 如图2—5所示,物体系由A、B、C三个物体构成,质量分别为mA、mB、mC.用一水平力F作用在小车C上,小车C在F的作用下运动时能使物体A和B相对于小车C处于静止状态.求连接A和B的不可伸长的线的张力T和力F的大小.(一切摩擦和绳、滑轮的质量都不计)
解析 在水平力F作用下,若A和B能相对于C静止,则它们对地必有相同的水平加速度.而A在绳的张力作用下只能产生水平向右的加速度,这就决定了F只能水平向右,可用整体法来求,而求张力必须用隔离法.
取物体系为研究对象,以地为参考系,受重力(mA+mB+mC)g,推力F和地面的弹力N,如图2—5甲所示,设对地的加速度为a,则有:
…………①
隔离B,以地为参考系,受重力mBg、张力T、C对B的弹力NB,应满足:
…………②
隔离A,以地为参考系,受重力mAg,绳的张力T,C的弹力NA,应满足;
NA=mAg…………③
T=mAa…………④
当绳和滑轮的质量以及摩擦都不计时,由②、④两式解出加速度
代入①式可得:
例6 如图2—6所示,一根轻质弹簧上端固定,下端挂一质量为m0的平盘,盘中有一物体质量为m,当盘静止时,弹簧的长度比其自然长度伸长了L,今向下拉盘,使弹簧再伸长△L后停止.然后松手放开,设弹簧总处在弹性限度以内,则刚松开手时盘对物体的支持力等于( )
A. B.
C. D.
解析 确定物体m的加速度可用整体法,确定盘对物体的支持力需用隔离法.选整体为研究对象,在没有向下拉盘时有
KL=(m+m0)g…………①
在向下拉伸△L又放手时有
K△L=(m+m0)a……②
再选m为研究对象 FN-mg=ma……③
解得:
应选A.此题也可用假设法、极限法求解.
例7 如图2—7所示,AO是质量为m的均匀细杆,可绕O轴在竖直平面内自动转动.细杆上的P点与放在水平桌面上的圆柱体接触,圆柱体靠在竖直的挡板上而保持平衡,已知杆的倾角为θ,AP长度是杆长的1/4,各处的摩擦都不计,则挡板对圆柱体的作用力等于 。
解析 求圆柱体对杆的支持力可用隔离法,用力矩平衡求解。求挡板对圆柱体的作用力可隔离圆柱体,用共点力的平衡来解.
以杆为研究对象,受力如图2—7甲所示,根据力矩平衡条件:
根据牛顿第三定律,杆对圆柱体的作用力与F大小相等,方向相反,再以圆柱体为研究对象,将力F正交分解,如图2—7—乙,在水平方向有
即挡板对圆柱体的作用力为.
例8 如图2—8所示,质量为m的小球被两个劲度系数皆为k的相同弹簧固定在一个质量为M的盒中,盒从h高处(自桌面量起)开始下落,在盒开始下落的瞬间,两弹簧未发生形变,小球相对盒静止,问下落的高度h为多少时,盒与桌面发生完全非弹性碰撞后还能再跳起来.
解析 盒下落过程可用整体法研究,下落后弹簧的形变情况应用隔离小球研究,盒起跳时可隔离盒研究。
在盒与桌面发生碰撞之前,小球仅受重力作用,着地时速度为:.
碰撞后盒静止,球先压缩下面的弹簧,同时拉上面的弹簧,当小球向下的速度减为零后,接着又向上运动,在弹簧原长位置上方x处,小球的速度又减为0,则在此过程中,对小球有:
把盒隔离出来,为使盒能跳起来,需满足:
例9 如图2—9所示,四个相等质量的质点由三根不可伸长的绳子依次连接,置于光滑水平面上,三根绳子形成半个正六边形保持静止。今有一冲量作用在质点A,并使这个质点速度变为u,方向沿绳向外,试求此瞬间质点D的速度.
解析 要想求此瞬间质点D的速度,由已知条件可知得用动量定理,由于A、B、C、D相关联,所以用隔离法,对B、C、D分别应用动量定理,即可求解.以B、C、D分别为研究对象,根据动量定理:
对B有:IA—IBcos60°=mBu…………①
IA cos60°—IB=mBu1…………②
对C有:IB—ID cos60°=mCu1……③
IBcos60°—ID=mcu2…………④
对D有:ID=mDu2……⑤
由①~⑤式解得D的速度
例10 有一个两端开口、粗细均匀的U形玻璃细管,放置在竖直平面内,处在压强为p0的大气中,两个竖直支管的高度均为h,水平管的长度为2h,玻璃细管的半径为r,r<
2.如将其中一个竖直支管的开口密封起来,使其管内气体压强为1个大气压.问当U形管绕以另一个竖直支管(开口的)为轴做匀速转动时,转数n应为多大才能使水平管内水银柱的长度稳定为(5/3)h(U形管做以上运动时,均不考虑管内水银液面的倾斜)
解析 如图2—10—甲所示,U形管右加速运动时,管内水银柱也要以同样加速度运动,所以A管内气体体积减小、压强增大,B管内气体体积增大、压强减小,水平管中液体在水平方向受力不平衡即产生加速度.若U形管以A管为轴匀速转动时,水平部分的液体也要受到水平方向的压力差而产生向心加速度.
1.当U形管以加速度a向右运动时,对水平管中水银柱有F1—F2=ma
即……①
……②
……③ 2—10—乙
将②、③式代入①式可得
2.如图2—10—乙,若U形管以A管为轴匀速转动时,对水平管中水银柱有F2—F1=ma.若转轴为n,则有:
……①
对B中气体有解得:……②
将②式代入①式可解得转速
例11 如图2—11所示,一个上下都与大气相通的竖直圆筒,内部横截面的面积S=0.01m2,中间用两个活塞A与B封住一定质量的理想气体,A、B都可沿圆筒无摩擦地上、下滑动,但不漏气,A的质量可不计,B的质量为M,并与一倔强系数k=5×103N/m的较长的弹簧相连.已知大气压强p0=1×105Pa,平衡时,两活塞间的距离l0=0.6m.现用力压A使之缓慢向下移动一定距离后,保持平衡,此时,用于压A的力F=5×102N.求活塞A向下移动的距离.(假定气体温度保持不变.)
解析 活塞A下移的距离应为B下降的距离与气体长度的减小量之和,B下降的距离可用整体法求解.气体长度的变化可隔离气体来求解.
选A、B活塞及气体为研究对象,设用力F向下压A时,活塞B下降的距离为x,
则有:F=kx…………①
选气体为研究对象,据玻意耳定律有…………②
解①②两式可得x=0.1m l=0.4m则活塞A下移的距离为:左=0.1+0.6—0.4=0.3m
例12 一个密闭的气缸,被活塞分成体积相等的左右两室,气缸壁与活塞是不导热的,它们之间没有摩擦,两室中气体的温度相等,如图2—12所示,现利用右室中的电热丝对右室中的气体加热一段时间,达到平衡后,左室的体积变为原来体积的3/4,气体的温度T1=300K.求右室中气体的温度.
解析 可隔离出A、B两部分气体,用理想气体状态方程求解.
设原来两室中气体的压强都为p,温度都为T,体积都为V,
对左边气体有……①对右边气体有②
①、②两式相比,可得右室中气体温度
例13 如图2—13所示,封闭气缸的活塞被很细的弹簧拉着,气缸内密封一定质量的气体,当温度为27℃时,弹簧的长度为30cm,此时缸内气体的压强为缸外大气压的1.2倍,当气温升到123℃时,弹簧的长度为36cm,求弹簧的原长.
解析 本题所研究的对象就是密封在气缸内的一定质量的气体,气体所处的初态为:
T1=300K、V1=SL1、(S为气缸横截面积,L1为弹簧长度)p1=p0+F1/S=1.2P0末态为T2=396K、V2=SL2 p2=p0+F2/S(p0为大气压强,F1、F2为弹簧的弹力).气体从初态过渡到末态时质量恒定,所以可利用状态方程求解:
将上述各状态参量代入状态方程:
解得:由于弹力产生的压强等于气缸内外气体的压强差,
所以: ①
②
联立①、②式得:
解得弹簧的原长为L0=20cm
例14 一个由绝缘细细构成的钢性圆形轨道,其半径为R,此轨道水平放置,圆心在O点,一个金属小珠P穿在此轨道上,可沿轨道无摩擦地滑动,小珠P带电荷Q.已知在轨道平面内A点(OA=r
由此得:
解①、②两式可得:A1点的位置距圆心O的距离为,所带电量
例15 如图2—15所示,两个电池组的电动势每节电池的内阻均为0.5Ω,R1=1Ω,R2=2Ω,R3=1.8Ω,求通过R1、R2、R3的电流及两个电池组的端电压各是多少?
解析 解此题时,可采用与力学隔离法相似
的解法,即采用电路隔离法.
气体从初态过渡到末态时质量恒定,所以可利用状态方程求解.
先将整个电路按虚线划分为Ⅰ、Ⅱ、Ⅲ三个部分,则有:
UAB=ε1—I1(R1+2r)……①
UAB=ε2—I2(R2+2r)………………②
UAB=I3R3……………………③
I1+I2=I3………………④
联立①②③④四式解得:I1=0.6A,I2=0.4A,I3=1A,电池组ε的端电压U1=2.4V,电池组ε2的端电压U2=2.6V.
例16 如图2—16所示,两根相互平行的间距L=0.4m的金属导轨水平放在B=0.2T的匀强磁场中,磁场垂直于导轨平面,导轨上的滑杆ab、cd所受摩擦力均为0.2N,两杆电阻均为0.1Ω,导轨电阻不计.当ab受到恒力F作用时,ab以v1做匀速运动,cd以v2做匀速运动,求通过ab杆的电流强度的大小和方向.
解析 要求通过ab杆的电流强度,应通过ab杆受的安培力求解,这就需要隔离出ab杆进行受力分析.
以ab杆为研究对象,因右手定则确定电流的方向为b→a,受力如图2—6—甲所示.因为ab杆匀速运动处于平衡状态,故有
F=f+BIL.
再以滑杆ab、cd整体作为研究对象,受力如图2—16—乙所示,因为ab、cd均做匀速运动,受力平衡,故有
代入上式,解得通过ab杆的电流为
所以通过ab杆的电流的大小为2.5A,方向b→a.
针对训练
1.质量为8kg的木块m放在质量为16kg的木板M上,并通过滑轮用细绳连接,如图2—17所示,M与m间,M与水平地面间的动摩擦因数μ均为0.25,滑轮摩擦不计.欲使M向匀速运动,水平拉力应为多大?(g取10m/s2)
2.在水平面上有两个物体A和B,它们之间用不可伸缩的质量不计的细绳连接起来,其中mA=3kg,mB=2kg,它们与地面间的动摩擦因数μ=0.1.如图2—18所示,今用一与水平方向成37°角、大小为10N的恒力拉B,使AB一起向右做匀加速直线运动,试求A对B的拉力.(g取10m/s2)
3.如图2—19所示,小物体m放在大物体M上,M系在固定于墙上的水平弹簧的另一端,并置于光滑水平面上,若弹簧的劲度系数为k,将M向右拉离平衡位置x后无初速度释放,在以后的运动中M与m保持相对静止,那么m在运动中受到的最大和最小摩擦力分别为多大?
4.电梯内有一个物体,质量为m,用细线挂在电梯的天花板上,当电梯以g/3的加速度竖直加速度竖直加速下降时(g为重力加速度),细线对物体的拉力为( )
A.2/3mg B.1/3mg C.4/3mg D.mg
5.两物体A和B,质量分别为m1和m2,互相接触放在光滑水平面上,如图2—20所示,对物体A施以水平的推力F,则物体A对物体B的作用力等于( )
A.m1F/(m1+m2) B.m2F/(m1+m2)
C.F D.m2/m1F
6.在光滑水平面上有一木板,一木棒A、B可沿水平轴O转动,其下端B搁在木板下,而整个系统处于静止状态(如图2—21所示).现在用水平力F向左推木板,但木板仍未动.由此可以得出结论:施力F后,木板和木棒之间的正压力( )
A.变大 B.不变
C.变小 D.条件不足,不能判断如何改变
7.如图2—22所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面木块压在上面的弹簧上(但不拴接),整个系统处于平衡状态.现缓慢向上提上面的木块,直到它刚离开上面弹簧,在这过程中下面木块移动的距离为( )
A.m1g/k1 B.m2g/k1
C.m1g/k2 D.m2g/k2
8.如图2—23,质量为2m的物块A与水平地面的摩擦可忽略不计,质量为m的物块B与地面的摩擦系数为μ.在已知水平推力F的作用下,AB做加速运动,A对B的作用力为 .
9.如图2—24所示,两块木块A和B,质量分别为mA和mB,紧挨着并排在水平桌面上,AB间的接触面垂直于图中纸面且与水平面成θ角。A、B间的接触面是光滑的,但它们与水平桌面间有摩擦,静摩擦系数和滑动摩擦系数均为μ.开始时A、B都静止,现施一水平推力F于A.要使A、B向右加速运动且A、B之间不发生相对滑动,则
(1)μ的数值应满足什么条件?
(2)推力F的最大值不能超过多少?
(只考虑平动,不考虑转动问题)
10.系统如图2—25所示,滑轮与绳的质量忽略,绳不可伸长。设系统所有部位都没有摩擦,物体B借助导轨(图中未画出来)被限定沿物体C的右侧面运动,试求物体C的运动加速度。
11.质量分别为m1、m2和m3的三个质点A、B、C位于光滑的水平桌面上,用已拉直的不可伸长的柔软的轻绳AB和BC连接,角ABC为为一锐角,如图2—26所示,今有一冲量为I的冲击力沿BC方向作用于质点C,求质点A开始运动时的速度.
12.如图2—27所示,四个质量均为m的质点,用同样长度且不可伸长的轻绳连结成菱形ABCD,静止放在水平光滑的桌面上.若突然给质点A一个力时极短沿CA方向的冲击,当冲击结束的时刻,质点A的速度为V,其他质点也获得一定的速度,.求此质点系统受到冲击后所具有的总动量和总能量.
13.如图2—28所示,一三角木块ABC置于光滑水平面上,两斜边与平面夹角分别为30°、60°.在斜边上有两个物体m1、m2,用不可伸长的细绳连接并跨在顶点A的定滑轮上,m1、m2可在斜面上无摩擦地滑动.已知木块的质量为M,三物体的质量比为m1:m2:M=4:1:16,滑轮光滑且质量可忽略.
(1)求M的加速度a及m1相对于M的加速度a′
(2)若m1从静止开始沿斜面移动20cm,求M沿水平面移动的距离.
14.如图2—29所示,可沿气缸壁自由活动的活塞将密封的圆筒形气缸分隔成A、B两部分.活塞与气缸顶部有一弹簧相连.当活塞位于气缸底部时弹簧恰好无形变,开始时B内充有一定量的气体,A内是真空,B部分高度为l1=0.10米,此时活塞受到的弹簧作用力与重力的大小相等.现将整个装置倒置.达到新的平衡后B部分的高度L2于多少?设温度不变.
15.图2—30中竖直圆筒是固定不动的,粗筒横截面积是细筒的4倍,细筒足够长.粗筒中A、B两轻质活塞间封有空气,气柱长l=20厘米.活塞A上方的水银深H=10厘米,两活塞与筒壁间的摩擦不计.用外力向上托住活塞B,使之处于平衡状态,水银面与粗筒上端相平.现使活塞B缓慢上移,直至水银的一半被推入细筒中,求活塞B上移的距离(设在整个过程中气柱的温度不变,大气压强p0相当于75厘米高的水银柱产生的压强).
16.如图2—31是容器的截面图,它是由A、B两部分构成,两部分都是圆筒形,高度都是h,底面积SB=S,SA=2S,容器下端有一小孔a与大气相通,上端开口,B中有一质量为m厚度不计的活塞,它与B的器壁有摩擦,最大摩擦力为f(f)mg,开始时活塞N位于B的最下端,已知大气压强为p0,当时温度为T0,现把a孔封闭,为保证封闭气体不与外界相通,筒中气体温度允许在多大范围内变化?
17.如图2—32所示,长为2l的圆形筒形气缸可沿摩擦因数为μ的水平面滑动,在气缸中央有一个截面积为S的活塞,气缸内气体的温度为T0,压强为p0(大气压强也为p0).在墙壁与活塞之间装有劲度系数为k的弹簧,当活塞处于如图位置时,弹簧恰好在原长位置.今使气缸内气体体积增加一倍,问气体的温度应达到多少?(气缸内壁光滑,活塞和气缸总质量为m).
18.A、B两带电小球,A固定不动,B的质量为m.在库仑作用下,B由静止开始运动.已知初始时A、B间的距离为d,B的加速度为a。经过一段时间后,B的加速度变为a/4,此时A、B间的距离应为 .已知此时B的速度为v,则在此过程中电势能的减少量为 .
19.如图2—33所示,是电磁流量计的示意图,在非磁性材料做成的圆管道外加一匀强磁场区域,当管中的导电液体流过磁场区域时,测出管壁上、下表面两点a、b间的电动势为ε,从而可求出管中液体在单位时间内的流量Q.已知圆管的内径为D,磁感应强度为B,试推导出Q与ε的关系表达式.
20.如图2—34所示,一矩形管中(管长为l,两侧面为导电面,并有导线在外面与之相连,上下面则为绝缘面)有电阻率为ρ的水银流动,当其一端加上压强p时,水银的流速为v0.现在竖直方向加上磁感应强度为B的匀强磁场.试证明:此时水银的流速为
.(设水银的速度与压强成正比)
答案:
1.F=100N 2.T=5.16N 3. 4.A 5.B 6.C 7.C
8. 9.(1) (2)F
10.
11.方向沿AB方向
12.P= E=
13.(1) (2) 3.78cm
14.0.2m 15.8cm 16.
17.摩擦力足够大时 摩擦力不是足够大时
18. 19. 20.证明略
EMBED Word.Picture.8
课件中心精品资料 www. 版权所有@课件中心 第 1 页 共 13 页
同课章节目录
