陕西省黄陵中学高新部2017-2018学年高二下学期期中考试数学(文)试题
文档属性
| 名称 | 陕西省黄陵中学高新部2017-2018学年高二下学期期中考试数学(文)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 239.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-18 00:00:00 | ||
图片预览


文档简介
高新高二中期考试
文科数学
一、选择题:本大题共12个小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。21教育网
1、已知集合A={1,2,3},B={x|(x+1)·(x-2)<0,x∈Z},则A∪B=( )
A.{1} B.{1,2}
C.{0,1,2,3} D.{-1,0,1,2,3}
2、设集合A={y|y=2x,x∈R},B={x|x2-1<0},则A∪B=( )
A.(-1,1) B.(0,1) C.(-1,+∞) D.(0,+∞)
3、已知a是实数,若复数是纯虚数,则a=( )
A.1 B.-1 C. D.-
4、观察下列各式:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…,则a10+b10等于( ) www.21-cn-jy.com
A.28 B.76 C.123 D.199
5.如右图,正三棱柱的各棱长都为2,分别
为AB、A1C1的中点,则EF的长( )
. . . .
6.一个几何体的三视图如图所示,则该几何体
的表面积为( )
A.20π B.28π C.24π D.32π
已知回归直线的斜率的估计值是1.23,样本点中心为(4,5),则回归直线方程是( )
A. B. C. D.
8.如图,在矩形ABCD中,点E为边CD的中点.若在矩形ABCD内部随机取一个点Q,则点Q取自△ABE内部的概率等于( D )21世纪教育网版权所有
A. B. C. D.
二、填空题:(本题共4小题,每小题5分,共20分)
13.已知向量=(﹣2,3),=(3,m),且,则m= .
14.函数f(x)= x+ex+1 在x =﹣1处的切线方程为 .
15.若x,y满足约束条件,则z= x +y的最大值为 .
16.设函数f(x)=,则满足f(x)+f(x﹣)>1的x的取值范围是 .
三、解答题:本题共6个小题,解答应写出文字说明、证明过程或演算步骤.
17.(本题满分10分) 在中,内角的对边分别为,且
(1)求角的值;
(2)若的面积为,的周长为,求边长
18.(本题满分12分)
在△ABC中,C=2A,a+c=5,cos A=,求b.
19. (本小题满分12分)已知平行四边形的三个顶点对应的复数为
(Ⅰ)求点B所对应的复数;
(Ⅱ)若,求复数所对应的点的轨迹.
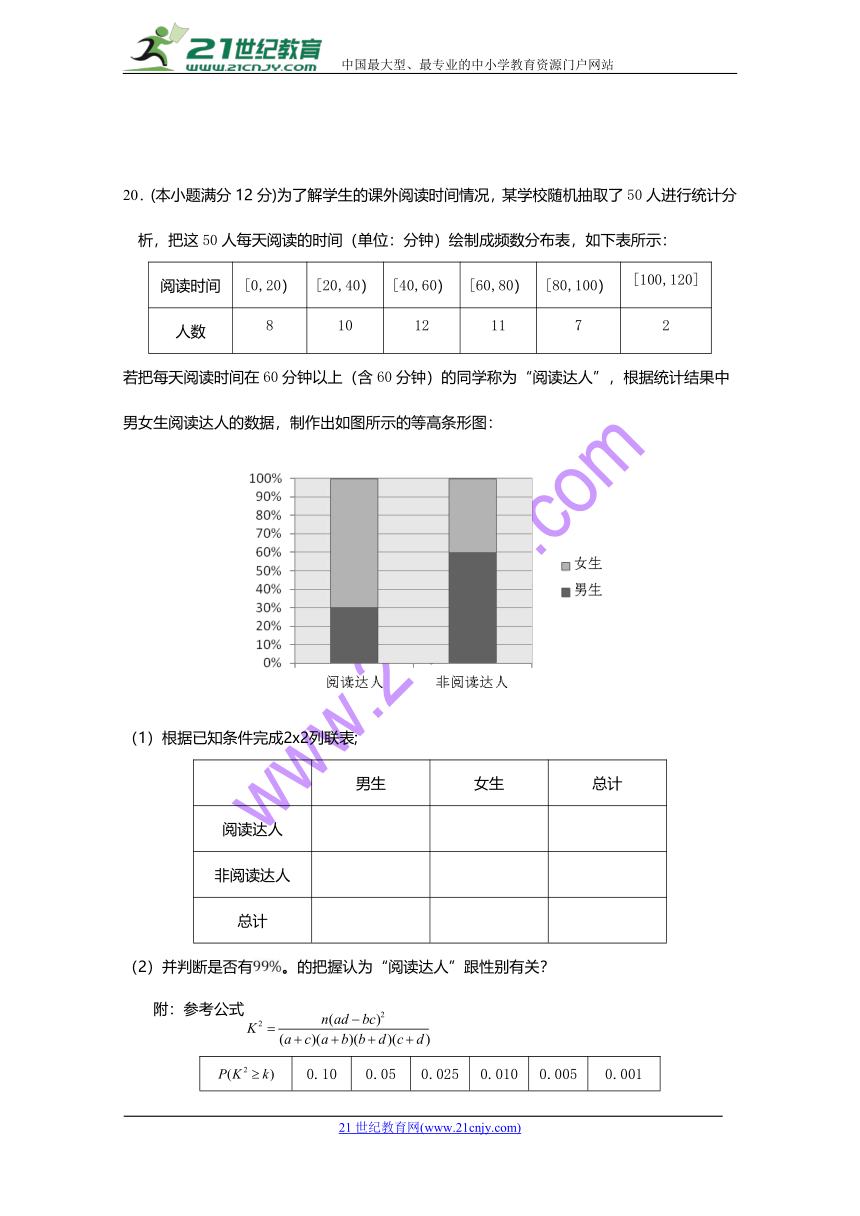
20.(本小题满分12分)为了解学生的课外阅读时间情况,某学校随机抽取了50人进行统计分析,把这50人每天阅读的时间(单位:分钟)绘制成频数分布表,如下表所示:
阅读时间
[0,20)
[20,40)
[40,60)
[60,80)
[80,100)
[100,120]
人数
8
10
12
11
7
2
若把每天阅读时间在60分钟以上(含60分钟)的同学称为“阅读达人”,根据统计结果中男女生阅读达人的数据,制作出如图所示的等高条形图:21cnjy.com
(1)根据已知条件完成2x2列联表;
男生
女生
总计
阅读达人
非阅读达人
总计
(2)并判断是否有。的把握认为“阅读达人”跟性别有关?
附:参考公式
0.10
0.05
0.025
0.010
0.005
0.001
2.706
3.841
5.024
6.635
7.879
10.828
21. (本小题满分12分)已知点P(0,-2),椭圆E:的离心率为,F是椭圆E的右焦点,直线PF的斜率为2,O为坐标原点.21·cn·jy·com
(1)求椭圆E的方程;
(2)直线l被圆O:x2+y2=3截得的弦长为3,且与椭圆E交于A、B两点,求△AOB面积的最大值.2·1·c·n·j·y
22. (本小题满分12分)已知函数f(x)=a--lnx,g(x)=ex-ex+1.
(1)若a=2,求函数f(x)在点(1,f(1))处的切线方程;
(2)若f(x)=0恰有一个解,求a的值;
(3)若g(x)≥f(x)恒成立,求实数a的取值范围.
1-4.CAAC 5-8.CBCD 9-12.DAAD
13.2; 14.2x﹣y+2=0; 15.8; 16.(,+∞);
17. (本小题满分12分)
解,,
,,,
,,.……………………………………………5分
,,
又,
,解得.……………………………………………………10分
18. 【答案】
【解析】由正弦定理,得,∴.
又a+c=5,∴a=2,c=3.
由余弦定理a2=b2+c2-2bccos A,得,∴b=2,或b=.
当b=2时,∵a=2,∴A=B. 又C=2A,且A+B+C=π,
∴,与已知矛盾,不合题意,舍去.
当b=时,满足题意.∴b=.
19.解:(1)由已知可得………………………………………2分
又…………………………………………………………………4分
所以所对应的复数为.………………………………………………………6分
(2)设复数所对应的点,
则表示复数所对应的点到复数所对应的点的距离为1,……9分
所以复数所对应的点的轨迹为以为圆心,1为半径的圆,且轨迹方程为
.…………………………………………………………12分
20.解:(1)由频数分布表得,“阅读达人”的人数是人…………2分
根据等高条形图得列联表
男生
女生
总计
阅读达人
6
14
20
非阅读达人
18
12
30
总计
24
26
50
…………………………………………………………………………………………………6分
(2)……………………………………9分
由于,故没有的把握认为“阅读达人”跟性别有关。………………12分
21.解:(1)因为蓄水池侧面的总成本为元,底面的总成本为元,
所以蓄水池的总成本为元.
又根据题意,
所以,………………………………………………………………3分
从而.……………………………………………………4分
因为,又由可得,
故函数的定义域为.…………………………………………………6分
(2)因为,
所以.
令,解得(舍去).
当时,,故在上为增函数;
当时, ,故在上为减函数.…………………10分
由此可知,在处取得最大值,此时.
即当,时,该蓄水池的体积最大.………………………………12分
22.【答案】(1)1;(2)
【解析】
(1)∵a=2,∴,f'(x)=,∴f'(1)=0,∴切线方程为y=1;
(2)令m(x)=+lnx,∴m'(x)=-+,
∴当x在(0,1)时,m'(x)>0,m(x)递增,
当x在(1,+∞)是,m'(x)<0,m(x)递减,
故m(x)的最大值为m(1)=1,
f(x)=0恰有一个解,即y=a,与m(x)只有一个交点,∴a=1;
(Ⅲ)由(Ⅱ)知函数的最大值为f(1)=a-1,g(x)=ex-ex+1.g'(x)=ex-e,
∴当x在(0,1)时,g'(x)<0,g(x)递减,
当x在(1,+∞)时,g'(x)>0,g(x)递增,
∴函数g(x)的最小值为g(1)=1,g(x)≥f(x)恒成立,∴1≥a-1,∴a≤2.
文科数学
一、选择题:本大题共12个小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。21教育网
1、已知集合A={1,2,3},B={x|(x+1)·(x-2)<0,x∈Z},则A∪B=( )
A.{1} B.{1,2}
C.{0,1,2,3} D.{-1,0,1,2,3}
2、设集合A={y|y=2x,x∈R},B={x|x2-1<0},则A∪B=( )
A.(-1,1) B.(0,1) C.(-1,+∞) D.(0,+∞)
3、已知a是实数,若复数是纯虚数,则a=( )
A.1 B.-1 C. D.-
4、观察下列各式:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11,…,则a10+b10等于( ) www.21-cn-jy.com
A.28 B.76 C.123 D.199
5.如右图,正三棱柱的各棱长都为2,分别
为AB、A1C1的中点,则EF的长( )
. . . .
6.一个几何体的三视图如图所示,则该几何体
的表面积为( )
A.20π B.28π C.24π D.32π
已知回归直线的斜率的估计值是1.23,样本点中心为(4,5),则回归直线方程是( )
A. B. C. D.
8.如图,在矩形ABCD中,点E为边CD的中点.若在矩形ABCD内部随机取一个点Q,则点Q取自△ABE内部的概率等于( D )21世纪教育网版权所有
A. B. C. D.
二、填空题:(本题共4小题,每小题5分,共20分)
13.已知向量=(﹣2,3),=(3,m),且,则m= .
14.函数f(x)= x+ex+1 在x =﹣1处的切线方程为 .
15.若x,y满足约束条件,则z= x +y的最大值为 .
16.设函数f(x)=,则满足f(x)+f(x﹣)>1的x的取值范围是 .
三、解答题:本题共6个小题,解答应写出文字说明、证明过程或演算步骤.
17.(本题满分10分) 在中,内角的对边分别为,且
(1)求角的值;
(2)若的面积为,的周长为,求边长
18.(本题满分12分)
在△ABC中,C=2A,a+c=5,cos A=,求b.
19. (本小题满分12分)已知平行四边形的三个顶点对应的复数为
(Ⅰ)求点B所对应的复数;
(Ⅱ)若,求复数所对应的点的轨迹.
20.(本小题满分12分)为了解学生的课外阅读时间情况,某学校随机抽取了50人进行统计分析,把这50人每天阅读的时间(单位:分钟)绘制成频数分布表,如下表所示:
阅读时间
[0,20)
[20,40)
[40,60)
[60,80)
[80,100)
[100,120]
人数
8
10
12
11
7
2
若把每天阅读时间在60分钟以上(含60分钟)的同学称为“阅读达人”,根据统计结果中男女生阅读达人的数据,制作出如图所示的等高条形图:21cnjy.com
(1)根据已知条件完成2x2列联表;
男生
女生
总计
阅读达人
非阅读达人
总计
(2)并判断是否有。的把握认为“阅读达人”跟性别有关?
附:参考公式
0.10
0.05
0.025
0.010
0.005
0.001
2.706
3.841
5.024
6.635
7.879
10.828
21. (本小题满分12分)已知点P(0,-2),椭圆E:的离心率为,F是椭圆E的右焦点,直线PF的斜率为2,O为坐标原点.21·cn·jy·com
(1)求椭圆E的方程;
(2)直线l被圆O:x2+y2=3截得的弦长为3,且与椭圆E交于A、B两点,求△AOB面积的最大值.2·1·c·n·j·y
22. (本小题满分12分)已知函数f(x)=a--lnx,g(x)=ex-ex+1.
(1)若a=2,求函数f(x)在点(1,f(1))处的切线方程;
(2)若f(x)=0恰有一个解,求a的值;
(3)若g(x)≥f(x)恒成立,求实数a的取值范围.
1-4.CAAC 5-8.CBCD 9-12.DAAD
13.2; 14.2x﹣y+2=0; 15.8; 16.(,+∞);
17. (本小题满分12分)
解,,
,,,
,,.……………………………………………5分
,,
又,
,解得.……………………………………………………10分
18. 【答案】
【解析】由正弦定理,得,∴.
又a+c=5,∴a=2,c=3.
由余弦定理a2=b2+c2-2bccos A,得,∴b=2,或b=.
当b=2时,∵a=2,∴A=B. 又C=2A,且A+B+C=π,
∴,与已知矛盾,不合题意,舍去.
当b=时,满足题意.∴b=.
19.解:(1)由已知可得………………………………………2分
又…………………………………………………………………4分
所以所对应的复数为.………………………………………………………6分
(2)设复数所对应的点,
则表示复数所对应的点到复数所对应的点的距离为1,……9分
所以复数所对应的点的轨迹为以为圆心,1为半径的圆,且轨迹方程为
.…………………………………………………………12分
20.解:(1)由频数分布表得,“阅读达人”的人数是人…………2分
根据等高条形图得列联表
男生
女生
总计
阅读达人
6
14
20
非阅读达人
18
12
30
总计
24
26
50
…………………………………………………………………………………………………6分
(2)……………………………………9分
由于,故没有的把握认为“阅读达人”跟性别有关。………………12分
21.解:(1)因为蓄水池侧面的总成本为元,底面的总成本为元,
所以蓄水池的总成本为元.
又根据题意,
所以,………………………………………………………………3分
从而.……………………………………………………4分
因为,又由可得,
故函数的定义域为.…………………………………………………6分
(2)因为,
所以.
令,解得(舍去).
当时,,故在上为增函数;
当时, ,故在上为减函数.…………………10分
由此可知,在处取得最大值,此时.
即当,时,该蓄水池的体积最大.………………………………12分
22.【答案】(1)1;(2)
【解析】
(1)∵a=2,∴,f'(x)=,∴f'(1)=0,∴切线方程为y=1;
(2)令m(x)=+lnx,∴m'(x)=-+,
∴当x在(0,1)时,m'(x)>0,m(x)递增,
当x在(1,+∞)是,m'(x)<0,m(x)递减,
故m(x)的最大值为m(1)=1,
f(x)=0恰有一个解,即y=a,与m(x)只有一个交点,∴a=1;
(Ⅲ)由(Ⅱ)知函数的最大值为f(1)=a-1,g(x)=ex-ex+1.g'(x)=ex-e,
∴当x在(0,1)时,g'(x)<0,g(x)递减,
当x在(1,+∞)时,g'(x)>0,g(x)递增,
∴函数g(x)的最小值为g(1)=1,g(x)≥f(x)恒成立,∴1≥a-1,∴a≤2.
同课章节目录
