通用版中考三轮冲刺复习动点综合问题(三)—双动点问题
文档属性
| 名称 | 通用版中考三轮冲刺复习动点综合问题(三)—双动点问题 |  | |
| 格式 | pptx | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-21 13:34:16 | ||
图片预览







文档简介
(共26张PPT)
动点综合问题(三)
通用版 中考复习
解读考点
知 识 点 名师点晴
动点问题中的特殊图形 等腰三角形与直角三角形 利用等腰三角形或直角三角形的特殊性质求解动点问题
相似问题 利用相似三角形的对应边成比例、对应角相等求解动点问题
动点问题中的计算问题 动点问题的最值与定值问题 理解最值或定值问题的求法
动点问题的面积问题 结合面积的计算方法来解决动点问题
动点问题的函数图象问题 一次函数或二次函数的图象 结合函数的图象解决动点问题
知识要点
专题三:双动点问题
点动、线动、形动构成的问题称之为动态几何问题. 它主要以几何图形为载体,运动变化为主线,集多个知识点为一体,集多种解题思想于一题. 这类题综合性强,能力要求高,它能全面的考查学生的实践操作能力,空间想象能力以及分析问题和解决问题的能力.
典型例题
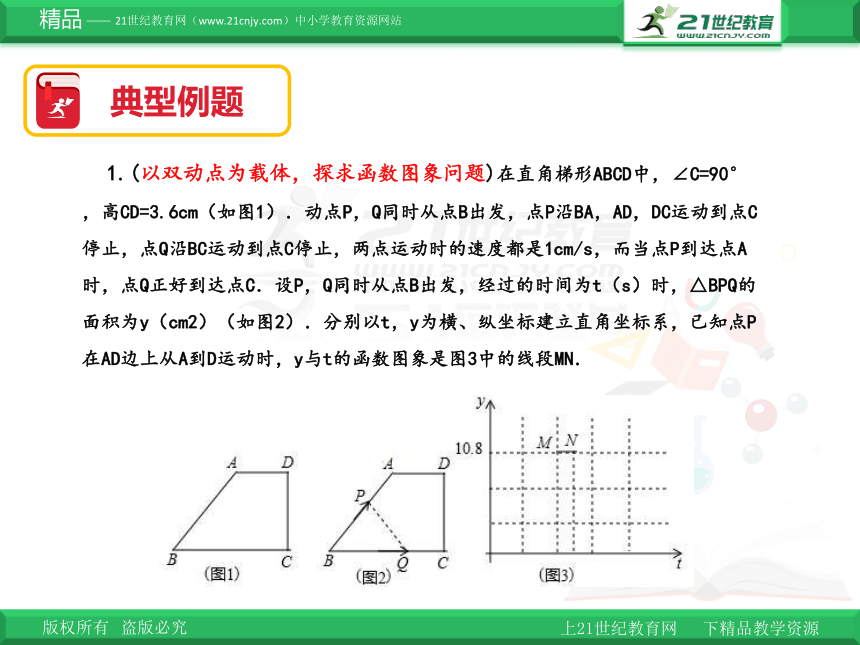
1.(以双动点为载体,探求函数图象问题)在直角梯形ABCD中,∠C=90°,高CD=3.6cm(如图1).动点P,Q同时从点B出发,点P沿BA,AD,DC运动到点C停止,点Q沿BC运动到点C停止,两点运动时的速度都是1cm/s,而当点P到达点A时,点Q正好到达点C.设P,Q同时从点B出发,经过的时间为t(s)时,△BPQ的面积为y(cm2)(如图2).分别以t,y为横、纵坐标建立直角坐标系,已知点P在AD边上从A到D运动时,y与t的函数图象是图3中的线段MN.
典型例题
1.(以双动点为载体,探求函数图象问题)在直角梯形ABCD中,∠C=90°,高CD=3.6cm(如图1).动点P,Q同时从点B出发,点P沿BA,AD,DC运动到点C停止,点Q沿BC运动到点C停止,两点运动时的速度都是1cm/s,而当点P到达点A时,点Q正好到达点C.设P,Q同时从点B出发,经过的时间为t(s)时,△BPQ的面积为y(cm2)(如图2).分别以t,y为横、纵坐标建立直角坐标系,已知点P在AD边上从A到D运动时,y与t的函数图象是图3中的线段MN.
(1)分别求出梯形中BA,AD的长度;
(2)分别写出点P在BA边上和DC边上运动时,y与t的函数关系式(注明自变量的取值范围),并在图3中补全整个运动中y关于t的函数关系的大致图象.
(3)问:是否存在这样的t,使PQ将梯形ABCD的面积恰好分成1:5的两部分?若存在,求出这样的t的值;若不存在,请说明理由.
典型例题
解析:(1)由于点P在AD运动时,点Q在C点,利用函数图象和三角形面积公式得到 ×BC×3.6=10.8,解得BC=6,而当点P到达点A时,点Q正好到达点C,所以AB=BC=6,作AH⊥BC于H,在Rt△ABH中,利用勾股计算出BH,则可求出CH的长,即可得出AD的长度.
(2)分类讨论:①当点P在BA上时,根据三角形面积公式得到
,②当点P在DC上时,y=-3t+32.4.
(3)分类讨论:当0≤t≤6,利用S△BPQ= S梯形ABCD及S△BPQ=
S梯形ABCD,求出时间t
典型例题
解:(1)点P在AD边上从A到D运动时,点Q在C点,
根据函数图象得到:
×BC×3.6=10.8,∴BC=6,
∵当点P到达点A时,点Q正好到达点C,∴AB=BC=6,
如图1,作AH⊥BC于H,在Rt△ABH中,
AB=6,AH=CD=3.6,
∴CH=BC-BH=6-4.8=1.2,
∴AD=1.2,即BA,AD的长度分别为6cm,1.2cm;
典型例题
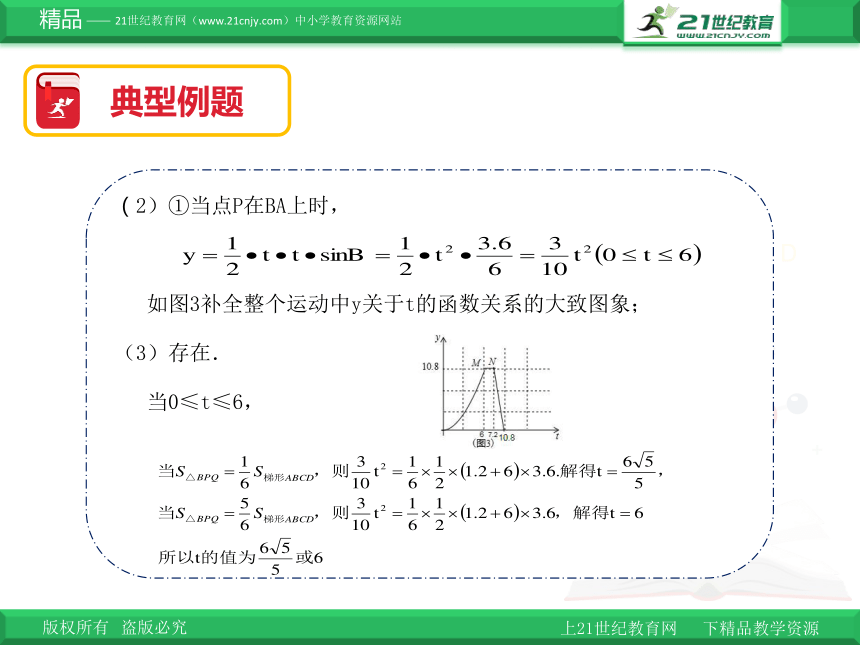
(2)①当点P在BA上时,
如图3补全整个运动中y关于t的函数关系的大致图象;
(3)存在.
当0≤t≤6,
典型例题
2.(以双动点为载体,探求结论开放性问题)如图①,Rt△ABC中,∠B=90°,∠CAB=30°,它的顶点A的坐标为(10,0),顶点B的坐标为(5, )AB=10,点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,设运动的时间为t秒.
典型例题
2.(以双动点为载体,探求结论开放性问题)如图①,Rt△ABC中,∠B=90°,∠CAB=30°,它的顶点A的坐标为(10,0),顶点B的坐标为(5, )AB=10,点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,设运动的时间为t秒.
(1)当点P在AB上运动时,△OPQ的面积S(平方单位)与时间t(秒)之间的函数图象为抛物线的一部分,(如图②),则点P的运动速度为 ;
(2)求(1)中面积S与时间t之间的函数关系式及面积S的最大值及S取最大值时点P的坐标;3)如果点P,Q保持(1)中的速度不变,那么点P沿AB边运动时,∠OPQ的大小随着时间t的增大而增大;沿着BC边运动时,∠OPQ的大小随着时间t的增大而减小,当点P沿这两边运动时,使∠OPQ=90°的点P有 个;
典型例题
解析:(1)利用图②中的函数图象,求得点P的运动时间与路程解决即可.(2)已知了AB的长和B点的坐标,那么sin∠BAO=
因此∠BAO=60°.根据(1)的求解过程即可得出S的解析式.然后根据函数的解析式来得出函数的最大值及此时对应的t的取值,然后根据P,Q的速度和t的取值,可求出P点的坐标.
典型例题
解析:(3)本题其实主要是看P在B点和C点时∠OPQ的度数范围,当∠OBQ的度数大于90°,∠OCQ的度数小于90°时,那么在AB,BC上分别有一个符合要求的点P,如果∠OBQ的度数小于90°时那么就没有符合要求的点,如果∠OBQ=90°,那么符合要求的点只有一个.当P,B重合时,作∠OPM=90°交y轴于点M,作PH⊥y轴于点H,然后比较OM和OQ的长即可得出∠OPQ的大致范围,根据相似三角形OPH和OPM不难得出OM的长,然后比较OM,OQ的大小,如果OQ>OM则说明∠OPQ>90°,反之则小于90°,用同样的方法可得出当P与C重合时∠OPQ的大致取值范围,然后根据上面的分析即可判定出有几个符合要求的点.
典型例题
解: (1)由图形可知,当点P运动了5秒时,它到达点B,此时AB=10,因此点P的运动速度为10÷5=2个单位/秒,
点P的运动速度为2个单位/秒.故答案是:2个单位/秒;
(2)如图①,过P作PM⊥x轴,∵点P的运动速度为2个单位/秒.
∴t秒钟走的路程为2t,即AP=2t,∵顶点B的坐标为(5, ),AB=10,∴sin∠BAO= ∴∠BAO=60°,∴∠APM=30°,
∴AM=t,又OA=10,∴OM=(10-t),即为△OPQ中OQ边上的高,
典型例题
而DQ=2t,OD=2,可得OQ=2t+2,
(3)当点P沿这两边运动时,∠OPQ=90°的点P有2个.
①当点P与点A重合时,∠OPQ<90°,
当点P运动到与点B重合时,OQ的长是12单位长度,
作∠OPM=90°交y轴于点M,作PH⊥y轴于点H,
由△OPH∽△OPM得:
典型例题
所以OQ>OM,从而∠OPQ>90度.
所以当点P在AB边上运动时,∠OPQ=90°的点P有1个.
②同理当点P在BC边上运动时,可算得
而构成直角时交y轴于
所以∠OCQ<90°,从而∠OPQ=90°的点P也有1个.
所以当点P沿这两边运动时,∠OPQ=90°的点P有2个.
故答案是:2.
典型例题
3.( 以双动点为载体,探求存在性问题) 如图,已知矩形ABCD中,AB=4cm,BC=a厘米(a>4).动点P、Q同时从C点出发,点P在线段CB上以1厘米/秒的速度由C点向B点运动,点Q在线段CD上以相同的速度由C点向D点运动,过点P作直线垂直于BC,分别交BQ、AD于点E、F,当点Q到达终点D时,点P随之停止运动.设运动时间为t秒(t>0).
(1)如图①,若a=5厘米,在运动过程中,当点E在矩形ABCD的对角线AC上时,求t的值;
(2)如图②,若a=6厘米,在运动过程中,是否存在某一时刻t,使得∠BFQ=90°?若存在,请求出此时t的值;若不存在,请说明理由;
(3)若经过t秒后,恰好使矩形ABPF的面积与直角三角形BCQ的面积相等,求a的取值范围.
典型例题
解析:
(1)根据平行线分线段成比例定理求出PF,得出
,代入求出即可;
(2)连接BF、FQ,根据勾股定理求出即可;
(3)根据面积公式求出t,根据t、a的取值求出即可.
典型例题
解:(1)∵EF∥AB, ∴△CEP∽△CAB,
∵EF∥CD,∴△BPE∽△BCQ,
解得t1=1,t2=0, ∵t>0,
∴t=1, 答:t的值是1秒.
典型例题
(2)连接BF、FQ,根据勾股定理得:BF +FQ =BQ ,
即4 +(6-t) +t +(4-t) =t +6 ,解得:t1=2,t2=8>4(舍去).答:在运动过程中,存在某一时刻t,使得 ∠BFQ=90°,此时t的值是2秒.
(3)根据面积公式得: at=4(a-t),∴at=8(a-t),
∴(a+8)t=8a, 解得:
根据题意得:t≤4,
∴a≤8,∵a>4,∴4<a≤8.答:a的取值范围是4<a≤8.
巩固提升
(以双动点为载体,探求函数最值问题 )如图1,P是⊙O外的一点,直线PO分别交⊙O于点A,B,则PA是点P到⊙O上的点的最短距离.
(1)探究一:如图2,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是弧CD 上的一个动点,连接AP,则AP的最小值是 .
(2)探究二:如图3,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,请求出A′C长度的最小值.
(3)探究三,在正方形ABCD中,点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,若AD=4,试求出线段CP的最小值.
巩固提升
解析:探究(一):如图1在⊙O上任取一点C(不为点A、B),连接PC、OC,证得PA<PC即可得到PA是点P到⊙O上的点的最短距离;图2中有圆,找到BC的中点E,连接AE,交半圆于P2,在半圆上取P1,连接AP1,EP1,可见,AP1+EP1>AE,即AP2是AP的最小值,再根据勾股定理求出AE的长,然后减掉半径即可;
探究(二)根据题意得出A′的位置,进而利用锐角三角函数关系求出A′C的长即可;
探究(三)由题意易证△ADE≌△DCF,从而得到AE=DF,∠DAE=∠CDF,再由等角的余角相等可得AE⊥DF;由于点P在运动中保持∠APD=90°,所以点P的路径是一段以AD为直径的弧,设AD的中点为Q,连接QC交弧于点P,此时CP的长度最小,再由勾股定理可得QC的长,再求CP即可.
巩固提升
解:(1)找到BC的中点E,连接AE,交半圆于P2,在半圆上任取P1,连接AP1,EP1,可见,AP1+EP1>AE,即AP2是AP的最小值.
在Rt△ABC中,∠ACB=90°,AC=BC=2,CE= BC=1
巩固提升
(2)如图所示:因为点M是AD的中点,
∴AM=MA′= AD=1,
由于△AMN沿MN所在的直线翻折得到△A′MN
∴MA′=AM=1是定值,当点A′在MC上时,A′C长度最小.
过点M作ME⊥DC于点E,
∵在边长为2的菱形ABCD中,∠A=60°
,M为AD中点,∴2MD=AD=CD=2,
∠EDM=60°,∴∠EMD=30°,
∴ED= MD= ,∴EM=DM×cos30°=
巩固提升
(3)∵四边形ABCD是正方形,
∴AD=DC=4,∠ADC=∠C=90°.
∴在△ADE和△DCF中,
∴△ADE≌△DCF(SAS).∴AE=DF,∠DAE=∠CDF,
由于∠CDF+∠ADF=90°,∴∠DAE+∠ADF=90°.
∴AE⊥DF;由于点P在运动中保持∠APD=90°,
∴点P的路径是一段以AD为直径的弧,设AD的中点为Q,连接QC交弧于点P,此时CP的长度最小,
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
动点综合问题(三)
通用版 中考复习
解读考点
知 识 点 名师点晴
动点问题中的特殊图形 等腰三角形与直角三角形 利用等腰三角形或直角三角形的特殊性质求解动点问题
相似问题 利用相似三角形的对应边成比例、对应角相等求解动点问题
动点问题中的计算问题 动点问题的最值与定值问题 理解最值或定值问题的求法
动点问题的面积问题 结合面积的计算方法来解决动点问题
动点问题的函数图象问题 一次函数或二次函数的图象 结合函数的图象解决动点问题
知识要点
专题三:双动点问题
点动、线动、形动构成的问题称之为动态几何问题. 它主要以几何图形为载体,运动变化为主线,集多个知识点为一体,集多种解题思想于一题. 这类题综合性强,能力要求高,它能全面的考查学生的实践操作能力,空间想象能力以及分析问题和解决问题的能力.
典型例题
1.(以双动点为载体,探求函数图象问题)在直角梯形ABCD中,∠C=90°,高CD=3.6cm(如图1).动点P,Q同时从点B出发,点P沿BA,AD,DC运动到点C停止,点Q沿BC运动到点C停止,两点运动时的速度都是1cm/s,而当点P到达点A时,点Q正好到达点C.设P,Q同时从点B出发,经过的时间为t(s)时,△BPQ的面积为y(cm2)(如图2).分别以t,y为横、纵坐标建立直角坐标系,已知点P在AD边上从A到D运动时,y与t的函数图象是图3中的线段MN.
典型例题
1.(以双动点为载体,探求函数图象问题)在直角梯形ABCD中,∠C=90°,高CD=3.6cm(如图1).动点P,Q同时从点B出发,点P沿BA,AD,DC运动到点C停止,点Q沿BC运动到点C停止,两点运动时的速度都是1cm/s,而当点P到达点A时,点Q正好到达点C.设P,Q同时从点B出发,经过的时间为t(s)时,△BPQ的面积为y(cm2)(如图2).分别以t,y为横、纵坐标建立直角坐标系,已知点P在AD边上从A到D运动时,y与t的函数图象是图3中的线段MN.
(1)分别求出梯形中BA,AD的长度;
(2)分别写出点P在BA边上和DC边上运动时,y与t的函数关系式(注明自变量的取值范围),并在图3中补全整个运动中y关于t的函数关系的大致图象.
(3)问:是否存在这样的t,使PQ将梯形ABCD的面积恰好分成1:5的两部分?若存在,求出这样的t的值;若不存在,请说明理由.
典型例题
解析:(1)由于点P在AD运动时,点Q在C点,利用函数图象和三角形面积公式得到 ×BC×3.6=10.8,解得BC=6,而当点P到达点A时,点Q正好到达点C,所以AB=BC=6,作AH⊥BC于H,在Rt△ABH中,利用勾股计算出BH,则可求出CH的长,即可得出AD的长度.
(2)分类讨论:①当点P在BA上时,根据三角形面积公式得到
,②当点P在DC上时,y=-3t+32.4.
(3)分类讨论:当0≤t≤6,利用S△BPQ= S梯形ABCD及S△BPQ=
S梯形ABCD,求出时间t
典型例题
解:(1)点P在AD边上从A到D运动时,点Q在C点,
根据函数图象得到:
×BC×3.6=10.8,∴BC=6,
∵当点P到达点A时,点Q正好到达点C,∴AB=BC=6,
如图1,作AH⊥BC于H,在Rt△ABH中,
AB=6,AH=CD=3.6,
∴CH=BC-BH=6-4.8=1.2,
∴AD=1.2,即BA,AD的长度分别为6cm,1.2cm;
典型例题
(2)①当点P在BA上时,
如图3补全整个运动中y关于t的函数关系的大致图象;
(3)存在.
当0≤t≤6,
典型例题
2.(以双动点为载体,探求结论开放性问题)如图①,Rt△ABC中,∠B=90°,∠CAB=30°,它的顶点A的坐标为(10,0),顶点B的坐标为(5, )AB=10,点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,设运动的时间为t秒.
典型例题
2.(以双动点为载体,探求结论开放性问题)如图①,Rt△ABC中,∠B=90°,∠CAB=30°,它的顶点A的坐标为(10,0),顶点B的坐标为(5, )AB=10,点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,设运动的时间为t秒.
(1)当点P在AB上运动时,△OPQ的面积S(平方单位)与时间t(秒)之间的函数图象为抛物线的一部分,(如图②),则点P的运动速度为 ;
(2)求(1)中面积S与时间t之间的函数关系式及面积S的最大值及S取最大值时点P的坐标;3)如果点P,Q保持(1)中的速度不变,那么点P沿AB边运动时,∠OPQ的大小随着时间t的增大而增大;沿着BC边运动时,∠OPQ的大小随着时间t的增大而减小,当点P沿这两边运动时,使∠OPQ=90°的点P有 个;
典型例题
解析:(1)利用图②中的函数图象,求得点P的运动时间与路程解决即可.(2)已知了AB的长和B点的坐标,那么sin∠BAO=
因此∠BAO=60°.根据(1)的求解过程即可得出S的解析式.然后根据函数的解析式来得出函数的最大值及此时对应的t的取值,然后根据P,Q的速度和t的取值,可求出P点的坐标.
典型例题
解析:(3)本题其实主要是看P在B点和C点时∠OPQ的度数范围,当∠OBQ的度数大于90°,∠OCQ的度数小于90°时,那么在AB,BC上分别有一个符合要求的点P,如果∠OBQ的度数小于90°时那么就没有符合要求的点,如果∠OBQ=90°,那么符合要求的点只有一个.当P,B重合时,作∠OPM=90°交y轴于点M,作PH⊥y轴于点H,然后比较OM和OQ的长即可得出∠OPQ的大致范围,根据相似三角形OPH和OPM不难得出OM的长,然后比较OM,OQ的大小,如果OQ>OM则说明∠OPQ>90°,反之则小于90°,用同样的方法可得出当P与C重合时∠OPQ的大致取值范围,然后根据上面的分析即可判定出有几个符合要求的点.
典型例题
解: (1)由图形可知,当点P运动了5秒时,它到达点B,此时AB=10,因此点P的运动速度为10÷5=2个单位/秒,
点P的运动速度为2个单位/秒.故答案是:2个单位/秒;
(2)如图①,过P作PM⊥x轴,∵点P的运动速度为2个单位/秒.
∴t秒钟走的路程为2t,即AP=2t,∵顶点B的坐标为(5, ),AB=10,∴sin∠BAO= ∴∠BAO=60°,∴∠APM=30°,
∴AM=t,又OA=10,∴OM=(10-t),即为△OPQ中OQ边上的高,
典型例题
而DQ=2t,OD=2,可得OQ=2t+2,
(3)当点P沿这两边运动时,∠OPQ=90°的点P有2个.
①当点P与点A重合时,∠OPQ<90°,
当点P运动到与点B重合时,OQ的长是12单位长度,
作∠OPM=90°交y轴于点M,作PH⊥y轴于点H,
由△OPH∽△OPM得:
典型例题
所以OQ>OM,从而∠OPQ>90度.
所以当点P在AB边上运动时,∠OPQ=90°的点P有1个.
②同理当点P在BC边上运动时,可算得
而构成直角时交y轴于
所以∠OCQ<90°,从而∠OPQ=90°的点P也有1个.
所以当点P沿这两边运动时,∠OPQ=90°的点P有2个.
故答案是:2.
典型例题
3.( 以双动点为载体,探求存在性问题) 如图,已知矩形ABCD中,AB=4cm,BC=a厘米(a>4).动点P、Q同时从C点出发,点P在线段CB上以1厘米/秒的速度由C点向B点运动,点Q在线段CD上以相同的速度由C点向D点运动,过点P作直线垂直于BC,分别交BQ、AD于点E、F,当点Q到达终点D时,点P随之停止运动.设运动时间为t秒(t>0).
(1)如图①,若a=5厘米,在运动过程中,当点E在矩形ABCD的对角线AC上时,求t的值;
(2)如图②,若a=6厘米,在运动过程中,是否存在某一时刻t,使得∠BFQ=90°?若存在,请求出此时t的值;若不存在,请说明理由;
(3)若经过t秒后,恰好使矩形ABPF的面积与直角三角形BCQ的面积相等,求a的取值范围.
典型例题
解析:
(1)根据平行线分线段成比例定理求出PF,得出
,代入求出即可;
(2)连接BF、FQ,根据勾股定理求出即可;
(3)根据面积公式求出t,根据t、a的取值求出即可.
典型例题
解:(1)∵EF∥AB, ∴△CEP∽△CAB,
∵EF∥CD,∴△BPE∽△BCQ,
解得t1=1,t2=0, ∵t>0,
∴t=1, 答:t的值是1秒.
典型例题
(2)连接BF、FQ,根据勾股定理得:BF +FQ =BQ ,
即4 +(6-t) +t +(4-t) =t +6 ,解得:t1=2,t2=8>4(舍去).答:在运动过程中,存在某一时刻t,使得 ∠BFQ=90°,此时t的值是2秒.
(3)根据面积公式得: at=4(a-t),∴at=8(a-t),
∴(a+8)t=8a, 解得:
根据题意得:t≤4,
∴a≤8,∵a>4,∴4<a≤8.答:a的取值范围是4<a≤8.
巩固提升
(以双动点为载体,探求函数最值问题 )如图1,P是⊙O外的一点,直线PO分别交⊙O于点A,B,则PA是点P到⊙O上的点的最短距离.
(1)探究一:如图2,在Rt△ABC中,∠ACB=90°,AC=BC=2,以BC为直径的半圆交AB于D,P是弧CD 上的一个动点,连接AP,则AP的最小值是 .
(2)探究二:如图3,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C,请求出A′C长度的最小值.
(3)探究三,在正方形ABCD中,点E,F分别从D,C两点同时出发,以相同的速度在直线DC,CB上移动,连接AE和DF交于点P,由于点E,F的移动,使得点P也随之运动,若AD=4,试求出线段CP的最小值.
巩固提升
解析:探究(一):如图1在⊙O上任取一点C(不为点A、B),连接PC、OC,证得PA<PC即可得到PA是点P到⊙O上的点的最短距离;图2中有圆,找到BC的中点E,连接AE,交半圆于P2,在半圆上取P1,连接AP1,EP1,可见,AP1+EP1>AE,即AP2是AP的最小值,再根据勾股定理求出AE的长,然后减掉半径即可;
探究(二)根据题意得出A′的位置,进而利用锐角三角函数关系求出A′C的长即可;
探究(三)由题意易证△ADE≌△DCF,从而得到AE=DF,∠DAE=∠CDF,再由等角的余角相等可得AE⊥DF;由于点P在运动中保持∠APD=90°,所以点P的路径是一段以AD为直径的弧,设AD的中点为Q,连接QC交弧于点P,此时CP的长度最小,再由勾股定理可得QC的长,再求CP即可.
巩固提升
解:(1)找到BC的中点E,连接AE,交半圆于P2,在半圆上任取P1,连接AP1,EP1,可见,AP1+EP1>AE,即AP2是AP的最小值.
在Rt△ABC中,∠ACB=90°,AC=BC=2,CE= BC=1
巩固提升
(2)如图所示:因为点M是AD的中点,
∴AM=MA′= AD=1,
由于△AMN沿MN所在的直线翻折得到△A′MN
∴MA′=AM=1是定值,当点A′在MC上时,A′C长度最小.
过点M作ME⊥DC于点E,
∵在边长为2的菱形ABCD中,∠A=60°
,M为AD中点,∴2MD=AD=CD=2,
∠EDM=60°,∴∠EMD=30°,
∴ED= MD= ,∴EM=DM×cos30°=
巩固提升
(3)∵四边形ABCD是正方形,
∴AD=DC=4,∠ADC=∠C=90°.
∴在△ADE和△DCF中,
∴△ADE≌△DCF(SAS).∴AE=DF,∠DAE=∠CDF,
由于∠CDF+∠ADF=90°,∴∠DAE+∠ADF=90°.
∴AE⊥DF;由于点P在运动中保持∠APD=90°,
∴点P的路径是一段以AD为直径的弧,设AD的中点为Q,连接QC交弧于点P,此时CP的长度最小,
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
同课章节目录
