牛顿运动定律的应用连接体

课件24张PPT。 牛顿运动定律的应用
—连接体 连接体是指两个或两个以上的物体组成的整体(系统)，并且整体(系统)内各物体间发生相互作用。
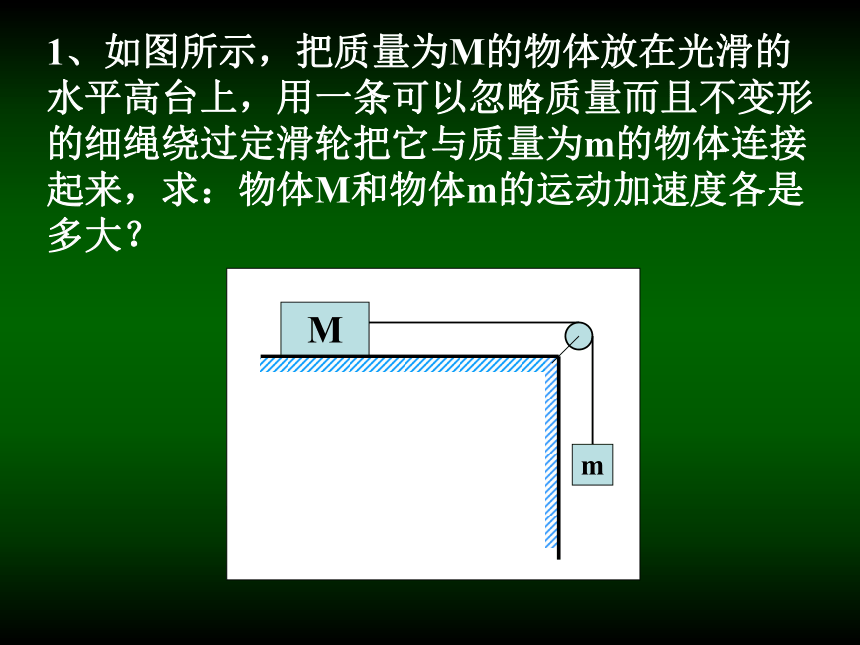
在“连接体问题”的解题中，常常要用到两种解题方法──“整体法”和“隔离法”。 1、如图所示，把质量为M的物体放在光滑的水平高台上，用一条可以忽略质量而且不变形的细绳绕过定滑轮把它与质量为m的物体连接起来，求：物体M和物体m的运动加速度各是多大？“隔离法”解题
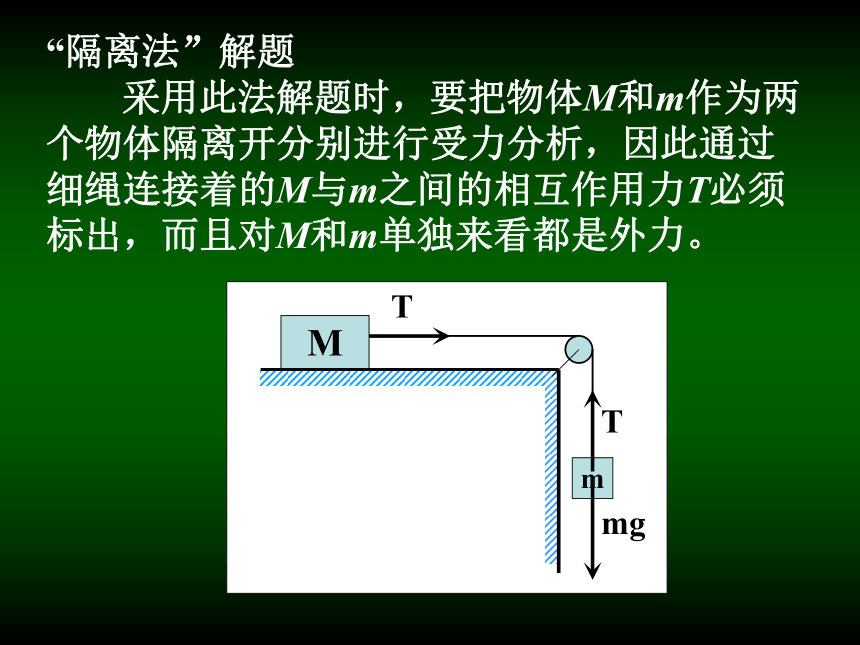
采用此法解题时，要把物体M和m作为两个物体隔离开分别进行受力分析，因此通过细绳连接着的M与m之间的相互作用力T必须标出，而且对M和m单独来看都是外力。对物体M：T＝Ma ①
对物体m：mg－T＝ma ②
将①式代入②式：
mg－Ma＝ma mg＝(M＋m)a
所以物体M和物体m所共有的加速度为： 把物体M和m看作一个整体，它们的总质量为(M＋m)。把通过细绳连接着的M与m之间的相互作用力看作是内力，既然水平高台是光滑无阻力的，那么这个整体所受的外力就只有mg了。M与m具有共同的加速度a。则可写出下列关系式： mg＝(M＋m)a，所以物体M和物体m所共有的加速度为：“整体法”解题练习：如图所示，用细绳连接绕过定滑轮的物体M和m，已知M>m，可忽略阻力，求物体M和m的共同加速度a。　　所谓隔离法就是将所研究的对象，从系统或全过程中隔离出来进行研究的方法.1、隔离法　　所谓整体法就是将两个或两个以上物体组成的整个系统或整个过程作为研究对象进行分析研究的方法.2、整体法 隔离法与整体法，不是相互对立的，一般问题的求解中，随着研究对象的转化，往往两种方法交叉运用，相辅相成。
所以，两种方法的取舍，并无绝对的界限，必须具体分析，灵活运用。无论哪种方法均以尽可能避免或减少非待求量（即中间未知量的出现，如非待求的力，非待求的中间状态或过程等）的出现为原则。 2、质量m＝1kg的物体放在倾角为θ＝370的斜面上，斜面的质量M＝2kg，斜面与物体间的动摩擦因数μ＝0.2，地面光滑，现对斜面体施加一水平推力，如图。要使物体m相对斜面静止，力F应为多大？（设物体与斜面的最大静摩擦力等于滑动摩擦力，g＝10m/s2）。（1）设物体处于相对斜面欲向下滑动的临界状态时推力为F1，此时物体所受摩擦力沿斜面向上，取加速度方向（水平向左）为x正方向，竖直向上为y轴正方向，根据牛顿第二定律，对m物体有：
x方向：
y方向：
对整体：
代入数值解得： （2）设物体处于相对斜面上滑动的临界状态时推力为F2，此时物体所受摩擦力沿斜面向下，根据牛顿第二定律，对m物体有：x方向：
y方向：
对整体：
代入数值解得：所以F的取值范围：14.34N≤F≤33.6N３、如图，质量为M的木板，放在倾角为θ的光滑斜面上，木板上一质量为m的人应以多大的加速度沿斜面往下跑，才能使木板静止在斜面上？ a M静止，其受合外力为0。M受到重力Mg、支持力N、人的摩擦力f 而平衡。
故： f ＝Mgsinθ
人受到重力mg、支持力N′、木板的摩擦力f
F合＝mgsinθ＋f
＝mgsinθ＋Mgsinθ
∴ a＝(m＋M)gsinθ/m解：（隔离法）思考题：为了保持人与斜面相对静止，木板运动的加速度是多少？a＝ (m＋M)gsinθ/M练习： 一只质量为m小猫，跳起来抓住悬在天花板上质量为M的竖直木杆，当小猫抓住木杆的瞬间，悬挂木杆的绳子断了，设木杆足够长，由于小猫不断地向上爬，可使小猫离地高度保持不变，则木杆下落的加速度为多大？ 练习：质量m＝10kg的木楔ABC静置于粗糙水平地面上，动摩擦因数μ＝0.02，在木楔的倾角θ为300的斜面上，有一质量m1＝1.0kg的物块由静止开始沿斜面下滑，当滑行路程x＝1.4m时，其速度v＝1.4m/s，在此过程中，木楔没有动，求地面对木楔的摩擦力的大小和方向。（g取10m/s2）f＝0.61N练习：如图所示，质量为M的木箱放在水平面上，木箱中的立杆上套着一个质量为m的小球，开始时小球在杆的顶端，由静止释放后，小球沿杆下滑的加速度为a，则小球在下滑的过程中，木箱对地面的压力为多少？解：（隔离法）
木箱与小球没有共同加速度，所以用隔离法. 取小球m为研究对象，受重力mg、摩擦力f，据牛顿第二定律得：mg－f＝ma ①mgfMgfNMgfN取木箱M为研究对象，受重力Mg、地面支持力N及小球给予的摩擦力f
据物体平衡条件得：
N－f－Mg＝0 ②
由①②式得N＝Mg＋m(g－a)B4、如图，物体A、B用细线连接绕过定光滑滑轮，物体C中央有开口，C放在B上。固定挡板D中央有孔，物体B可以穿过它而物体C又恰好能被挡住。物体A、B、C的质量MA＝0.8kg、MB＝MC＝0. 1kg，物体B、C一起从静止开始下降H1＝0.50m后，C被固定挡板D截住， B继续下降H2＝0.30m后停止。求：物体A与平面的滑动摩擦系数μ＝？AC解：（整体法）
当C与B一起下降时，系统加速度为a1，到C被D挡住时，B的速度为vB当C被抵挡住，B下降的过程中系统加速度为a2 (系统在减速) μ＝0.2 练习: A的质量m1＝4m ，B的质量m2＝m ，斜面固定在水平地面上。开始时将B按在地面上不动，然后放手，让A沿斜面下滑而B上升。A与斜面无摩擦，如图 。设当A沿斜面下滑s距离后，细线突然断了。求B离开地面上升的最大高度H。 H ＝ 1.2s