5.2.2平行线的判定(共25张PPT)
文档属性
| 名称 | 5.2.2平行线的判定(共25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 743.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-23 06:15:20 | ||
图片预览




文档简介
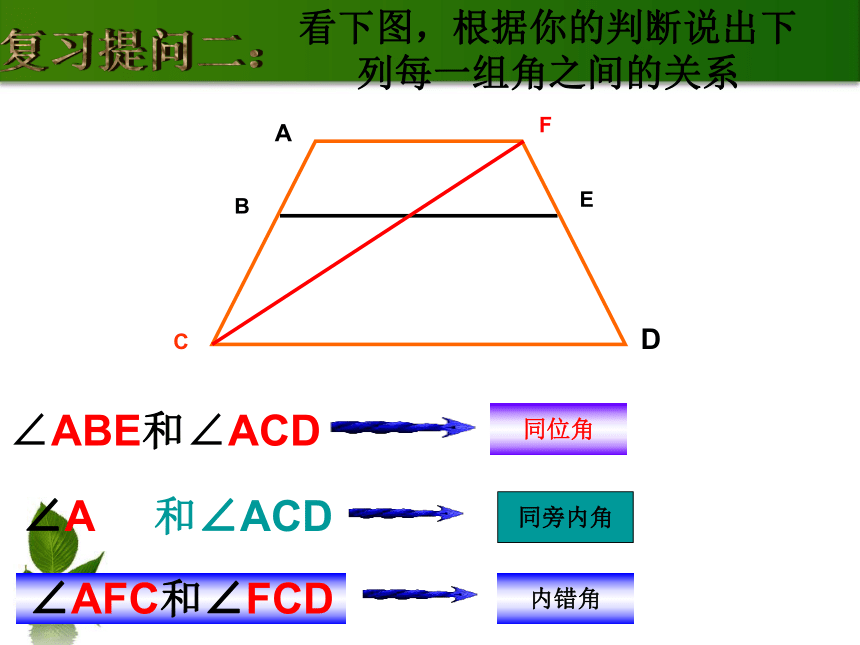
课件25张PPT。第五章 相交线与平行线5.2 平行线及其判定5.2.2 平行线的判定1、同学们根据前面所学内容,看下图请找出哪些角是内错角哪些角是同位角哪些角是同旁内角哪些角是对顶角 它们有什么联系23415786复习提问:课前热身看下图,根据你的判断说出下列每一组角之间的关系∠ABE和∠ACD ∠A 和∠ACD∠AFC和∠FCD同位角同旁内角内错角复习提问二:复习提问三:
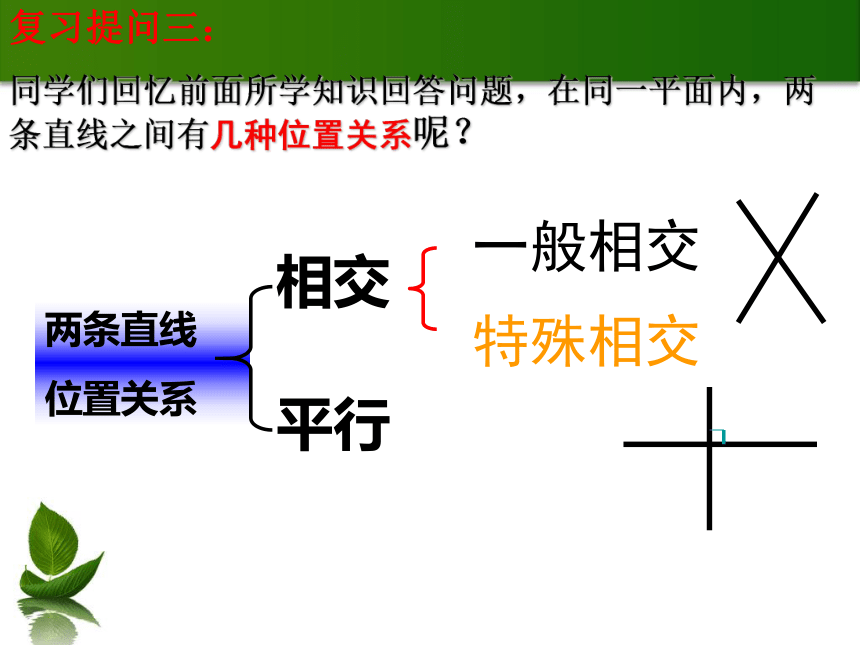
同学们回忆前面所学知识回答问题,在同一平面内,两条直线之间有几种位置关系呢? 一般相交特殊相交两条直线
位置关系判断下列语句是否正确:(1) 两条直线不相交,就叫做平行线. ( )(2) 与一条直线平行的直线只有一条. ( )(3) 如果两条直线a、b都和直线c平行,
那么直线a、b就平行. ( )×√×热身训练 判定两条直线平行的方法有两种:定义:在同一平面内,不相交的两条直线叫平行线.平行公理的推论同学们可以想一想?
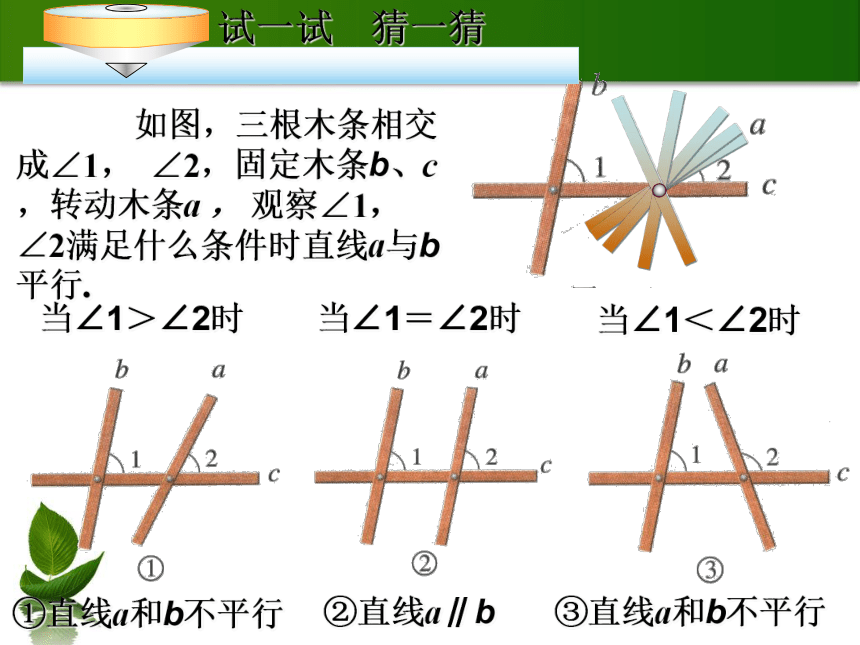
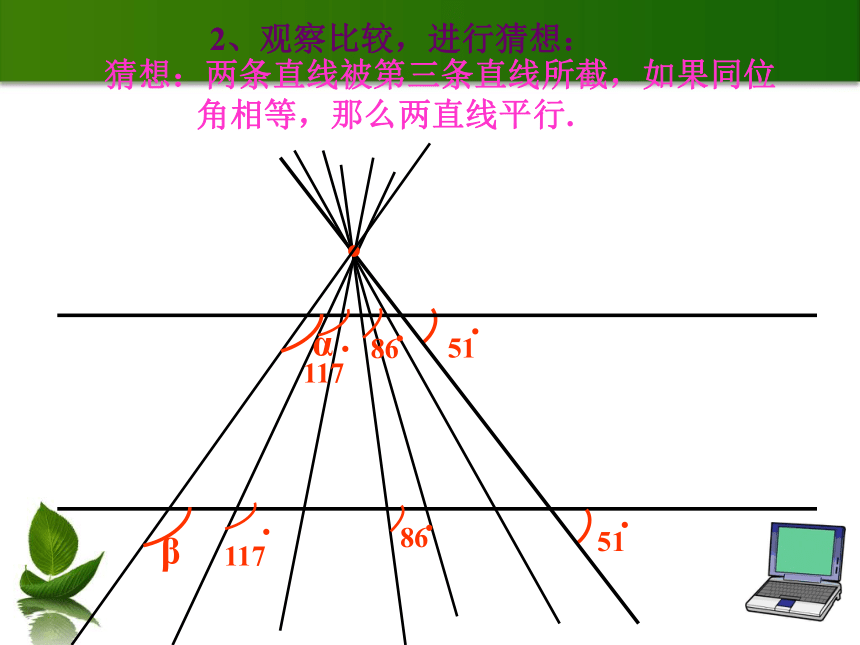
除应用以上两种方法以外,是否还有其它方法呢?如果两条直线同平行于一条直线,那么两条直线平行. 如图,三根木条相交成∠1, ∠2,固定木条b、c,转动木条a , 观察∠1, ∠2满足什么条件时直线a与b平行.当∠1=∠2时①直线a和b不平行②直线a∥b③直线a和b不平行 猜想:两条直线被第三条直线所截,如果同位
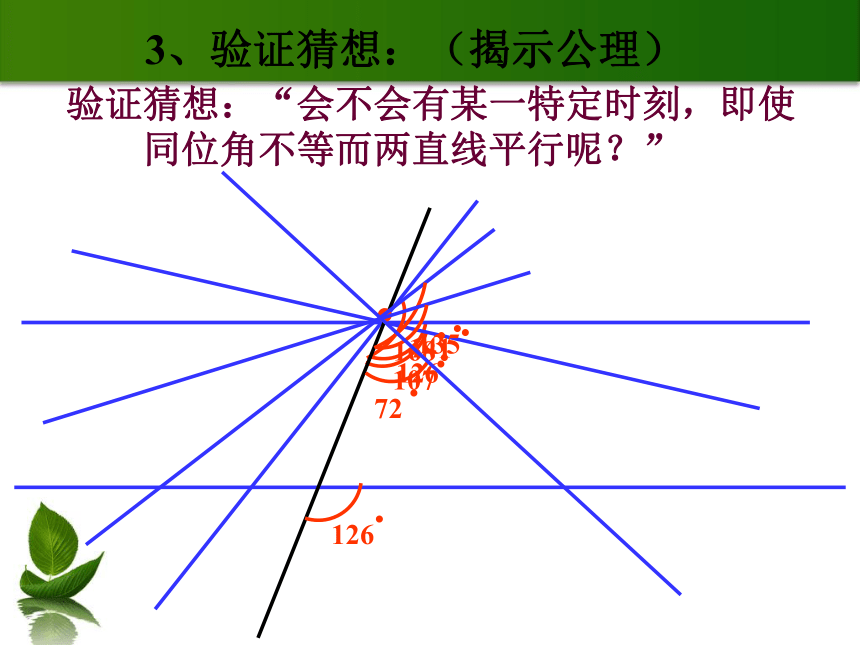
角相等,那么两直线平行..2、观察比较,进行猜想:验证猜想:“会不会有某一特定时刻,即使
同位角不等而两直线平行呢?”.3、验证猜想:(揭示公理) 两条直线被第三条直线所截,如果同
位角相等,那么这两条直线平行.简单说成:同位角相等、两直线平行判定两条直线平行的公理:3、验证猜想:(揭示公理)推理过程:
∵∠α = ∠ β(已知)
∴a ∥ b(同位角相等、两直线平行) 一般地,判断两直线平行有下面的方法: 两条直线被第三条直线所截 ,如果同位角相等,那么这两条直线平行.简单地说,同位角相等,两直线平行.如图,哪两个角相等能判定直线AB∥CD?如果 , 能判定哪两条直线平行? ∠1 =∠2∠3=∠4AB∥CDEF∥GH∠3 =∠4∠2 =∠5EF∥GH如图,已知∠1+∠2=180o,AB与CD平行吗?为什么?ABCDEF123例2 已知:如图,ABC、CDE都是直线, 且∠1=∠2,∠1=∠C,
求证:AC∥FD.
∵ ∠1 = ∠2,
∠1 = ∠C (已知), ∴ ∠2=∠C (等量代换). ∴ AC∥FD (同位角相等,两直线平行). FEBCDA21证明:如图,已知∠1=∠2,AB与CD平行吗?为什么?ABCDEF12 一般地,判断两直线平行有下面的方法: 两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.简单地说,内错角相等,两直线平行.如图,哪两个角相等能判定直线AB∥CD?如果 , 能判定哪两条直线平行? ∠3 =∠2∠3=∠4或∠1=∠4AB∥CDAB∥CD∠5 =∠6∠4 =∠5EF∥GH6例4 已知:如图,∠DAB被AC平分,
且∠1=∠3,
ABCD123求证:AB∥CD.
∵ ∠DAB被AC平分 (已知) ∴ ∠1=∠2 (角平分线定义) ∵ ∠1=∠3 (已知) ∴ ∠2=∠3 (等量代换) ∴ AB∥CD ( 内错角相等,两直线平行 ) 证明:如图,已知∠1+∠2=180o,AB与CD平行吗?为什么?ABCDEF12 一般地,判断两直线平行有下面的方法: 两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行.简单地说,同旁内角互补,两直线平行. 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?abc12∵ b⊥a,∴∠2=90° .(垂直的定义)∴b∥c. (同位角相等,两直线平行)∴∠1=90°. (垂直的定义)∵ c ⊥a,∴∠1=∠2.想一想判定两直线平行有哪些方法?理由:平行理由:如图,
∵ b⊥a,c⊥a,(已知)
∴∠1=∠2=90°.(垂直定义)
∴b∥c.(内错角相等,两直线平行)abc12方法2:理由:如图,
∵ b⊥a,c⊥a,(已知)
∴∠1=∠2=90°.(垂直定义)
∴ ∠1+∠2=180°.
∴b∥c.(同旁内角互补,两直线平行)abc12方法3:结论在同一平面内,如果两条直线都和第三条直线垂直,那么这两条直线平行.bca1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.如果两条直线都与第三条直线平行,
那么这两条直线也互相平行.
5.在同一平面内,如果两条直线都垂直于
同一条直线,那么这两条直线平行.
判定两条直线是否平行的方法有:这节课我们学了什么?平行线判定方法1:同位角相等,两直线平行.
平行线判定方法2:内错角相等,两直线平行.
平行线判定方法2:同旁内角互补,两直线平行.你记住了吗? 我们活着不能与草木同腐,不能醉生梦死,枉度人生,要有所作为.
——方志敏
同学们回忆前面所学知识回答问题,在同一平面内,两条直线之间有几种位置关系呢? 一般相交特殊相交两条直线
位置关系判断下列语句是否正确:(1) 两条直线不相交,就叫做平行线. ( )(2) 与一条直线平行的直线只有一条. ( )(3) 如果两条直线a、b都和直线c平行,
那么直线a、b就平行. ( )×√×热身训练 判定两条直线平行的方法有两种:定义:在同一平面内,不相交的两条直线叫平行线.平行公理的推论同学们可以想一想?
除应用以上两种方法以外,是否还有其它方法呢?如果两条直线同平行于一条直线,那么两条直线平行. 如图,三根木条相交成∠1, ∠2,固定木条b、c,转动木条a , 观察∠1, ∠2满足什么条件时直线a与b平行.当∠1=∠2时①直线a和b不平行②直线a∥b③直线a和b不平行 猜想:两条直线被第三条直线所截,如果同位
角相等,那么两直线平行..2、观察比较,进行猜想:验证猜想:“会不会有某一特定时刻,即使
同位角不等而两直线平行呢?”.3、验证猜想:(揭示公理) 两条直线被第三条直线所截,如果同
位角相等,那么这两条直线平行.简单说成:同位角相等、两直线平行判定两条直线平行的公理:3、验证猜想:(揭示公理)推理过程:
∵∠α = ∠ β(已知)
∴a ∥ b(同位角相等、两直线平行) 一般地,判断两直线平行有下面的方法: 两条直线被第三条直线所截 ,如果同位角相等,那么这两条直线平行.简单地说,同位角相等,两直线平行.如图,哪两个角相等能判定直线AB∥CD?如果 , 能判定哪两条直线平行? ∠1 =∠2∠3=∠4AB∥CDEF∥GH∠3 =∠4∠2 =∠5EF∥GH如图,已知∠1+∠2=180o,AB与CD平行吗?为什么?ABCDEF123例2 已知:如图,ABC、CDE都是直线, 且∠1=∠2,∠1=∠C,
求证:AC∥FD.
∵ ∠1 = ∠2,
∠1 = ∠C (已知), ∴ ∠2=∠C (等量代换). ∴ AC∥FD (同位角相等,两直线平行). FEBCDA21证明:如图,已知∠1=∠2,AB与CD平行吗?为什么?ABCDEF12 一般地,判断两直线平行有下面的方法: 两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.简单地说,内错角相等,两直线平行.如图,哪两个角相等能判定直线AB∥CD?如果 , 能判定哪两条直线平行? ∠3 =∠2∠3=∠4或∠1=∠4AB∥CDAB∥CD∠5 =∠6∠4 =∠5EF∥GH6例4 已知:如图,∠DAB被AC平分,
且∠1=∠3,
ABCD123求证:AB∥CD.
∵ ∠DAB被AC平分 (已知) ∴ ∠1=∠2 (角平分线定义) ∵ ∠1=∠3 (已知) ∴ ∠2=∠3 (等量代换) ∴ AB∥CD ( 内错角相等,两直线平行 ) 证明:如图,已知∠1+∠2=180o,AB与CD平行吗?为什么?ABCDEF12 一般地,判断两直线平行有下面的方法: 两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行.简单地说,同旁内角互补,两直线平行. 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?abc12∵ b⊥a,∴∠2=90° .(垂直的定义)∴b∥c. (同位角相等,两直线平行)∴∠1=90°. (垂直的定义)∵ c ⊥a,∴∠1=∠2.想一想判定两直线平行有哪些方法?理由:平行理由:如图,
∵ b⊥a,c⊥a,(已知)
∴∠1=∠2=90°.(垂直定义)
∴b∥c.(内错角相等,两直线平行)abc12方法2:理由:如图,
∵ b⊥a,c⊥a,(已知)
∴∠1=∠2=90°.(垂直定义)
∴ ∠1+∠2=180°.
∴b∥c.(同旁内角互补,两直线平行)abc12方法3:结论在同一平面内,如果两条直线都和第三条直线垂直,那么这两条直线平行.bca1.同位角相等, 两直线平行.
2.内错角相等, 两直线平行.
3.同旁内角互补, 两直线平行.
4.如果两条直线都与第三条直线平行,
那么这两条直线也互相平行.
5.在同一平面内,如果两条直线都垂直于
同一条直线,那么这两条直线平行.
判定两条直线是否平行的方法有:这节课我们学了什么?平行线判定方法1:同位角相等,两直线平行.
平行线判定方法2:内错角相等,两直线平行.
平行线判定方法2:同旁内角互补,两直线平行.你记住了吗? 我们活着不能与草木同腐,不能醉生梦死,枉度人生,要有所作为.
——方志敏
