湖南省张家界市永定区2017-2018学年八年级下学期期中教学质量检测数学试题(Word版,含简略答案)
文档属性
| 名称 | 湖南省张家界市永定区2017-2018学年八年级下学期期中教学质量检测数学试题(Word版,含简略答案) |  | |
| 格式 | zip | ||
| 文件大小 | 181.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-22 17:02:23 | ||
图片预览

文档简介
二○一八年春季期中教学质量检测
八年级 数学
考生注意:本卷共三道题,满分120分,时量120分钟。
一、选择题(本大题共8个小题,每小题3分,满分24分.请将正确答案的字母代号填在下表中.)
1.下列图形中,既是轴对称图形又是中心对称图形的是
A B C D
2.如图,∠ACB=90°,CD⊥AB,垂足为D,下列结论错误的是
A.图中有三个直角三角形 B.∠1=∠2
C.∠1和∠B都是∠A的余角 D.∠2=∠A
3.如果等边三角形的边长为12,那么该等边三角形的一条中位线长为
A.2 B.4 C.6 D.8
4.顺次连接矩形各边中点所得的四边形是
A.矩形 B.梯形 C.菱形 D.正方形
5.下列说法中正确的是
A.已知是三角形的三边长,则
B.在直角三角形中,两边长的平方和等于第三边长的平方
C.在Rt△ABC中,若∠A=90°,则
D.在Rt△ABC中,若∠C=90°,则
6.下面条件中,能判定四边形是平行四边形的条件是
A.对角线互相平分 B.一组对角相等
C.一组对边相等 D.对角线互相垂直
7.一个多边形每个外角都是60°,这个多边形的外角和为
A.180° B.360° C.720° D.1080°
8.如右图,过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,连接AE、CF.若AB=,∠DCF=30°,则EF的长为
A.2 B.3 C. D.
二、填空题(本大题共8小题,每小题3分,满分24分)
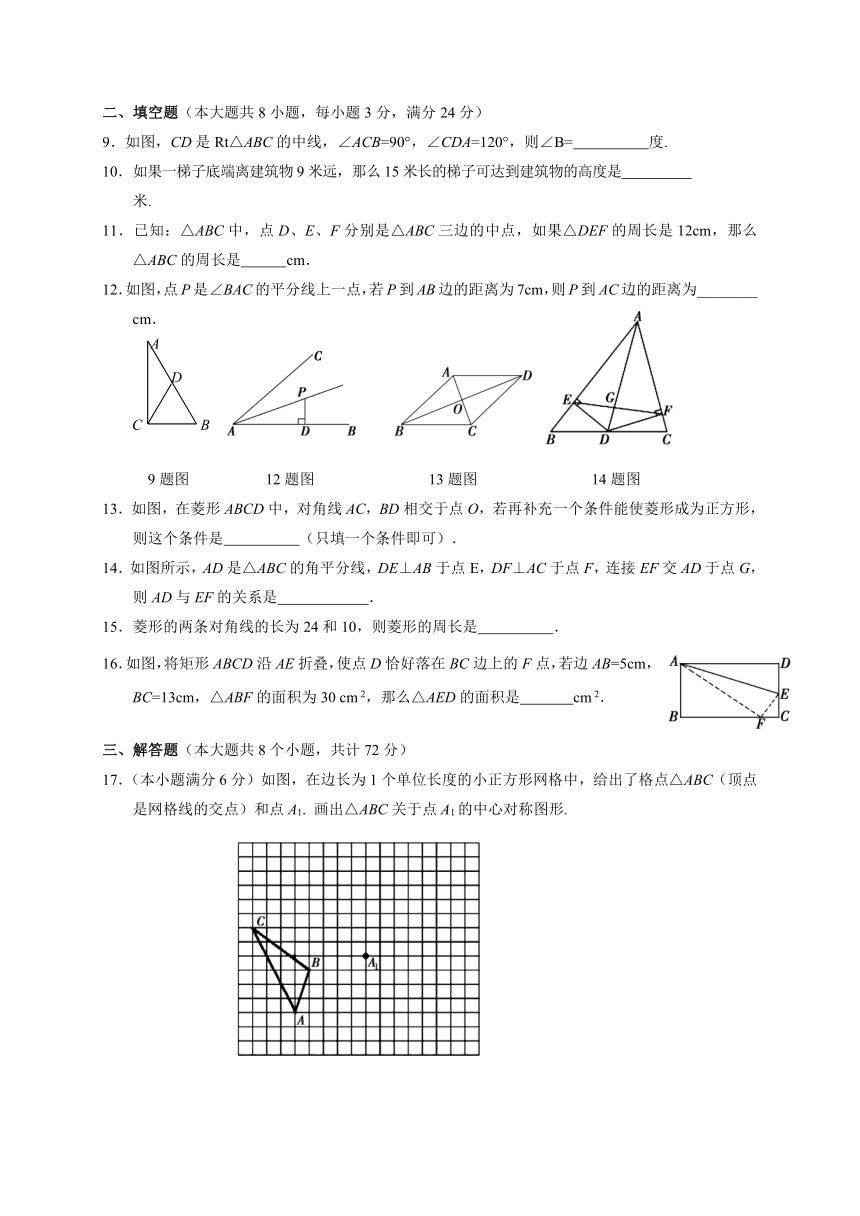
9.如图,CD是Rt△ABC的中线,∠ACB=90°,∠CDA=120°,则∠B= 度.
10.如果一梯子底端离建筑物9米远,那么15米长的梯子可达到建筑物的高度是
米.
11.已知:△ABC中,点D、E、F分别是△ABC三边的中点,如果△DEF的周长是12cm,那么△ABC的周长是 cm.
12.如图,点P是∠BAC的平分线上一点,若P到AB边的距离为7cm,则P到AC边的距离为________ cm.
9题图 12题图 13题图 14题图
13.如图,在菱形ABCD中,对角线AC,BD相交于点O,若再补充一个条件能使菱形成为正方形,则这个条件是 (只填一个条件即可).
14.如图所示,AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点G,则AD与EF的关系是 .
15.菱形的两条对角线的长为24和10,则菱形的周长是 .
16.如图,将矩形ABCD沿AE折叠,使点D恰好落在BC边上的F点,若边AB=5cm,BC=13cm,△ABF的面积为30 cm 2,那么△AED的面积是 cm 2.
三、解答题(本大题共8个小题,共计72分)
17.(本小题满分6分)如图,在边长为1个单位长度的小正方形网格中,给出了格点△ABC(顶点是网格线的交点)和点A1. 画出△ABC关于点A1的中心对称图形.
18.(本小题满分8分)已知:如图,矩形ABCD中,E、F是AB上的两点,且AF=BE.求证:∠ADE=∠BCF.
19.(本小题满分8分)如果一个多边形的内角和是外角和的3倍还多180°,那么这个多边形的边数是多少?
20.(本小题满分8分)如图,△ABC中,AB=AC,∠C=30°,AB⊥AD,AD=2cm,求BC的长.
21.(本小题满分10分)如图,在ABCD中,E、F分别是AB、DC边上的点,且AE=CF,
(1)求证:△ADE≌△CBF.
(2)若∠DEB=90°,求证:四边形DEBF是矩形.
22.(本小题满分10分)正方形ABCD中,AE=CF,则四边形BEDF是菱形吗?请说明理由.
23.(本小题满分10分)如图,在ABCD中,M、N是对角线BD上的两点,BN=DM,请判断AM与CN有怎样的关系,并说明理由.
24.(本小题满分12分)如图,矩形ABCD中,点P是线段AD上的一个动点,O为BD的中点,PO的延长线交BC于Q.
(1)求证:OP=OQ;
(2)若AD=8cm,AB=6cm,点P从点A出发,以1cm/s的速度向点D运动(不与D重合). 设点P运动的时间为t秒,请用t表示PD的长;
(3)当t为何值时,四边形PBQD是菱形?
二○一八年春季期中教学质量检测
八年级数学参考答案
一、选择题(本大题共8小题,每小题3分,满分24分)
题号 1 2 3 4 5 6 7 8
答案 B B C C D A B A
二、填空题(本大题共8小题,每小题3分,满分24分)
9.60 10.12 11.24 12.7
13.略 14.垂直平分 15.52 16.16.9
三、解答题(本大题共9个小题,共计72分)
17.略
18.略
19.多边形的边数是9
20.BC=6cm
21.略
22.略
23.平行且相等,理由略
24.(1)略 ………………4分
(2) ………………8分
(3),,解得. ………………12分
A
B
C
D
八年级 数学
考生注意:本卷共三道题,满分120分,时量120分钟。
一、选择题(本大题共8个小题,每小题3分,满分24分.请将正确答案的字母代号填在下表中.)
1.下列图形中,既是轴对称图形又是中心对称图形的是
A B C D
2.如图,∠ACB=90°,CD⊥AB,垂足为D,下列结论错误的是
A.图中有三个直角三角形 B.∠1=∠2
C.∠1和∠B都是∠A的余角 D.∠2=∠A
3.如果等边三角形的边长为12,那么该等边三角形的一条中位线长为
A.2 B.4 C.6 D.8
4.顺次连接矩形各边中点所得的四边形是
A.矩形 B.梯形 C.菱形 D.正方形
5.下列说法中正确的是
A.已知是三角形的三边长,则
B.在直角三角形中,两边长的平方和等于第三边长的平方
C.在Rt△ABC中,若∠A=90°,则
D.在Rt△ABC中,若∠C=90°,则
6.下面条件中,能判定四边形是平行四边形的条件是
A.对角线互相平分 B.一组对角相等
C.一组对边相等 D.对角线互相垂直
7.一个多边形每个外角都是60°,这个多边形的外角和为
A.180° B.360° C.720° D.1080°
8.如右图,过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,连接AE、CF.若AB=,∠DCF=30°,则EF的长为
A.2 B.3 C. D.
二、填空题(本大题共8小题,每小题3分,满分24分)
9.如图,CD是Rt△ABC的中线,∠ACB=90°,∠CDA=120°,则∠B= 度.
10.如果一梯子底端离建筑物9米远,那么15米长的梯子可达到建筑物的高度是
米.
11.已知:△ABC中,点D、E、F分别是△ABC三边的中点,如果△DEF的周长是12cm,那么△ABC的周长是 cm.
12.如图,点P是∠BAC的平分线上一点,若P到AB边的距离为7cm,则P到AC边的距离为________ cm.
9题图 12题图 13题图 14题图
13.如图,在菱形ABCD中,对角线AC,BD相交于点O,若再补充一个条件能使菱形成为正方形,则这个条件是 (只填一个条件即可).
14.如图所示,AD是△ABC的角平分线,DE⊥AB于点E,DF⊥AC于点F,连接EF交AD于点G,则AD与EF的关系是 .
15.菱形的两条对角线的长为24和10,则菱形的周长是 .
16.如图,将矩形ABCD沿AE折叠,使点D恰好落在BC边上的F点,若边AB=5cm,BC=13cm,△ABF的面积为30 cm 2,那么△AED的面积是 cm 2.
三、解答题(本大题共8个小题,共计72分)
17.(本小题满分6分)如图,在边长为1个单位长度的小正方形网格中,给出了格点△ABC(顶点是网格线的交点)和点A1. 画出△ABC关于点A1的中心对称图形.
18.(本小题满分8分)已知:如图,矩形ABCD中,E、F是AB上的两点,且AF=BE.求证:∠ADE=∠BCF.
19.(本小题满分8分)如果一个多边形的内角和是外角和的3倍还多180°,那么这个多边形的边数是多少?
20.(本小题满分8分)如图,△ABC中,AB=AC,∠C=30°,AB⊥AD,AD=2cm,求BC的长.
21.(本小题满分10分)如图,在ABCD中,E、F分别是AB、DC边上的点,且AE=CF,
(1)求证:△ADE≌△CBF.
(2)若∠DEB=90°,求证:四边形DEBF是矩形.
22.(本小题满分10分)正方形ABCD中,AE=CF,则四边形BEDF是菱形吗?请说明理由.
23.(本小题满分10分)如图,在ABCD中,M、N是对角线BD上的两点,BN=DM,请判断AM与CN有怎样的关系,并说明理由.
24.(本小题满分12分)如图,矩形ABCD中,点P是线段AD上的一个动点,O为BD的中点,PO的延长线交BC于Q.
(1)求证:OP=OQ;
(2)若AD=8cm,AB=6cm,点P从点A出发,以1cm/s的速度向点D运动(不与D重合). 设点P运动的时间为t秒,请用t表示PD的长;
(3)当t为何值时,四边形PBQD是菱形?
二○一八年春季期中教学质量检测
八年级数学参考答案
一、选择题(本大题共8小题,每小题3分,满分24分)
题号 1 2 3 4 5 6 7 8
答案 B B C C D A B A
二、填空题(本大题共8小题,每小题3分,满分24分)
9.60 10.12 11.24 12.7
13.略 14.垂直平分 15.52 16.16.9
三、解答题(本大题共9个小题,共计72分)
17.略
18.略
19.多边形的边数是9
20.BC=6cm
21.略
22.略
23.平行且相等,理由略
24.(1)略 ………………4分
(2) ………………8分
(3),,解得. ………………12分
A
B
C
D
同课章节目录
