北师大版七下册4.5利用三角形全等测距离 课件(共26张PPT)
文档属性
| 名称 | 北师大版七下册4.5利用三角形全等测距离 课件(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-22 21:12:28 | ||
图片预览




文档简介
课件26张PPT。4.5利用三角形全等测距离(1)回顾判断两个三角形全等的条件
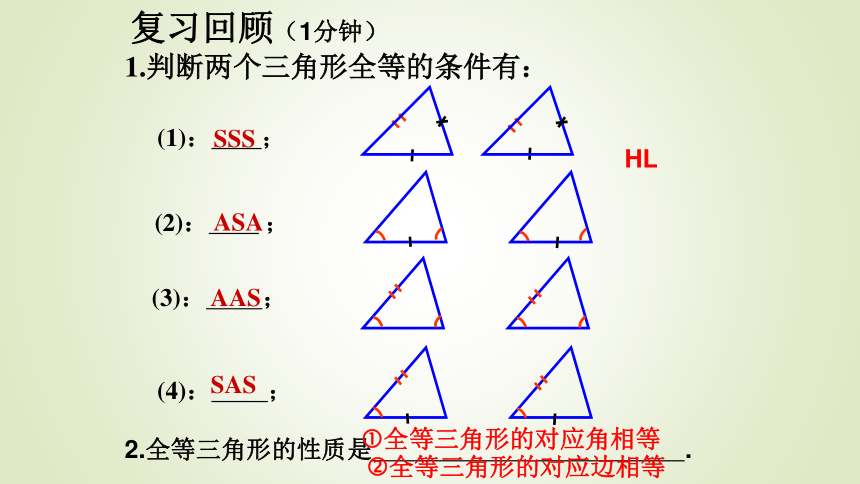
(2)能从实例中构建全等三角形,用以解决问题。学习目标 (1分钟)1.判断两个三角形全等的条件有:(1): ;(2): ;(3): ;SSSASAAAS复习回顾(1分钟)(4): ;SAS2.全等三角形的性质是 .?全等三角形的对应边相等?全等三角形的对应角相等HL如图,已知∠1=∠2,AC=AD,增加下列条件:
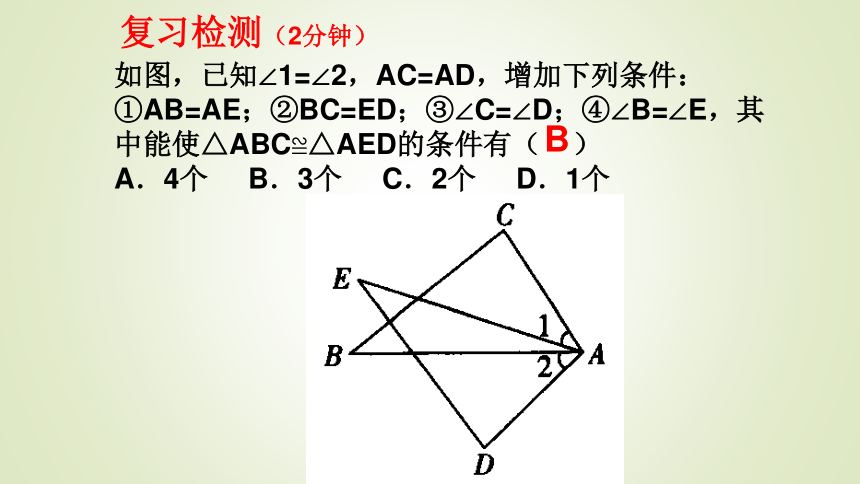
①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E,其中能使△ABC≌△AED的条件有( )
A.4个 B.3个 C.2个 D.1个复习检测(2分钟)B下面是一位经历过战争的老人讲述的一个故事: 在一次战役中,我军阵地与敌军碉堡隔河相望.为了炸掉这个碉堡,需要知道碉堡与我军阵地的距离.在不能过河测量又没有任何测量工具的情况下,如何估测这个距离呢?探究:利用三角形全等测距离 他面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部;
然后,他转过一个角度,保持刚才的姿态,这时视线落在了自己所在岸的某一点上;
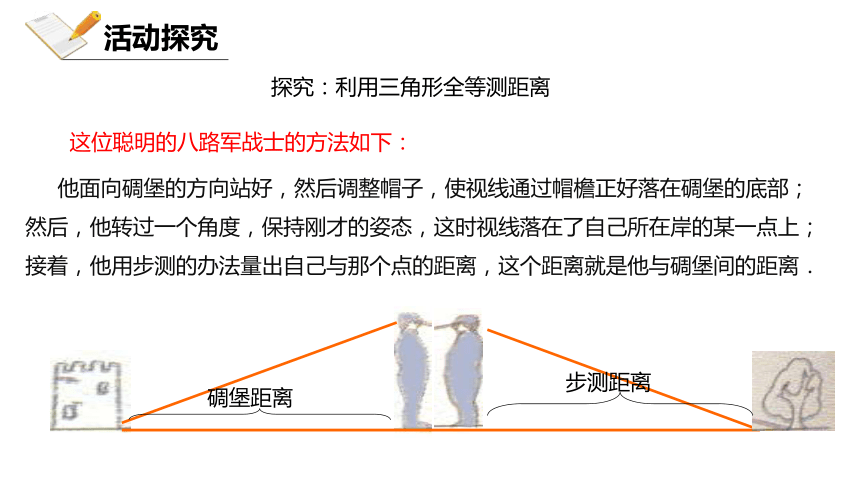
接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡间的距离.这位聪明的八路军战士的方法如下:阅读相关内容完成下列问题:
(1)在引例中,“保持刚才的姿态”你是怎样理解的?
答:___________________.
(2)直立的姿态从而保证了两个三角形中的两个_____;帽檐不动,保证了视线和身体的_____不变.
(3)要说明图中两个三角形全等,已知两角,则还差一边,即_________.
(4)测量的原理是:构造了_______________.直立姿态和帽檐不动直角夹角身高不变两个全等三角形构造全等三角形自学指导(一)(5分钟)
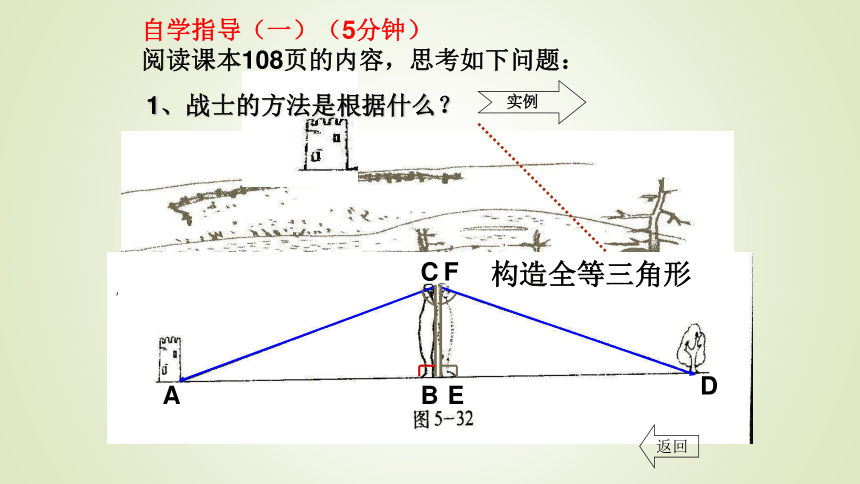
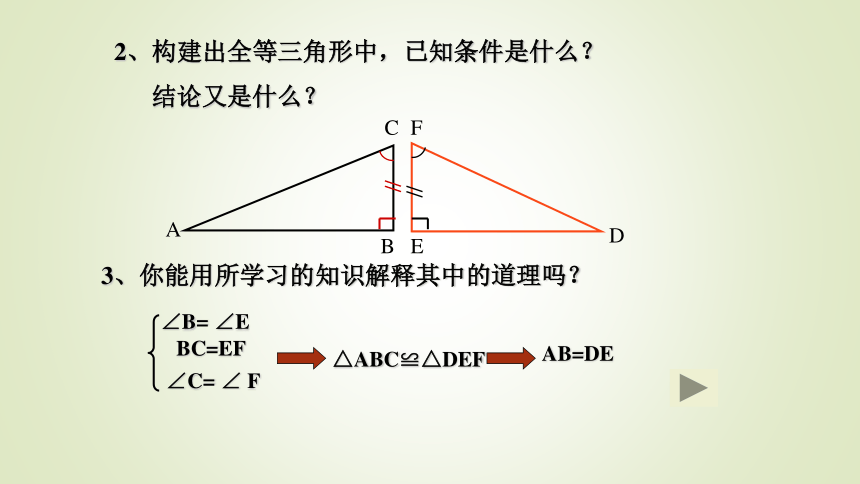
阅读课本108页的内容,思考如下问题:1、战士的方法是根据什么?2、构建出全等三角形中,已知条件是什么?
结论又是什么?3、你能用所学习的知识解释其中的道理吗?ABCDEF∠B= ∠EBC=EF∠C= ∠ F△ABC≌△DEFAB=DE利用三角形全等测距离的实质是什么?
其实质为构造三角形全等,
根据全等三角形对应边相等,
将不可测的线段的长度,
转化为可测线段长度.1.如图所示小明设计了一种测工件内径AB的卡钳,问:在卡钳的设计中,AO、BO、CO、DO 应满足下列的哪个条件?( )
A、AO=CO
B、BO=DO
C、AC=BD
D、AO=CO且BO=DOD自学检测(一) (4分钟)2、如图,工人师傅要计算一个圆柱形容器的容积,需要测量其内径。现在有两根同样长的木棒、一条橡皮绳和一把带有刻度的直尺,你能想法帮助他完成吗?·中点CAB先在地上取一个可以直接到达 A 点和B点的点C,连接 AC 并延长到 D,使CD= CA;连接BC并延长到E,使CE= CB,连接DE并测量出它的长度,DE的长度就是 A,B 间的距离.BA·CDE····P108 想一想: 如图,A,B 两点分别位于一个池塘的两端,小明想用绳子测量 A,B 间的距离,但绳子不够长,一个叔叔帮他出了这样一个主意:BA··CDE···自学指导(二)(6+3分钟)
阅读课本108页“想一想” 思考如下问题;
1、仿照指导(一)的方法,构建三角形,并写出“已
知”、“求证”的内容。已知:CA=CD,CB=CE, ∠ACB= ∠ DCE
求证:AB=DE。2、你能设计出其它的方案来吗?(构建全等三角形)3、已知条件是什么?结论又是什么?4、你能说明设计出方案的理由吗?BA·····CED如图,已知AB⊥BF,DG⊥BF,BC=DC,
求证:AB=DE。FG1、如图要测量河两岸相对的两点A、B的距离,先在AB 的垂线BF上取两点C、D,使CD=CB,再定出BF的垂线DE,可以证明△EDC≌△ABC,得ED=AB,因此,测得ED的长就是AB的长。判定△EDC≌△ABC的理由是( )
A、SSS B、ASA C、AAS D、SASB自学检测(二)(5+2分钟)2、如图,山脚下有A、B两点,要测出A、B两点的距离。 (1)在地上取一个可以直接到达A、B点的点O,连接AO并延长AO到C,使AO=CO,你能完成剩下的图形吗?(2)说明你是如何求AB的距离。??解:在△AOB与△COD中,AO = CO∠ AOB = ∠CODBO = DO∴△AOB≌△ COD(SAS)∴ AB=CD (全等三角形的对应边相等)即:通过测量C、D之间的距离可以求A、B的距离(已知)(对顶角相等)(已知)选择恰当的判断条件构造全等三角形说明理由(证明 )下结论方法点拨:当堂训练(10分钟)1.如图,A、B、C、D是四个村庄,B、C、D在一条东西 走向公路的沿线上,BD=1千米,DC=1千米,村AC、AD间也有公路相连且AC=3千米,只有AB之间由于间隔了一个小湖,所以无直接相连的公路,现决定在湖面上造一座斜拉桥,测得AE=1.2千米,BF=0.7千米,则斜拉桥长至少有 千米D1.12.如图,公园里有一条“z”字形道路ABCD,其中AB∥CD,在AB、BC、CD三段路旁各有一只小凳E、M、F,M恰为BC的中点,且E、F、M在同一条直线上,在BE道路上停放着一排小汽车,从而无法直接测量B、E之间的距离,你能想出解决的办法吗?试说明理由。ACBDEMF在△EMB和△FMC中,∠ B = ∠C∴△ EMB ≌△ FMC (ASA)∴ EB=FC (全等三角形的对应边相等)(已证)(已证)BM = CM ∠ EMB = ∠FMC(对顶角相等)解:如图所示,连接E、M、F
∵AB∥CD
∴∠B=∠C ( 两直线平行,
内错角相等 )
∵ M是BC的中点,
∴BM=CM (中点的定义)即:通过测量F、C之间的距离可以求E、B的距离ACBDEMF1、如图,要量河两岸相对两点A、B的距离。
下图是一位同学利用三角形全等所画的图,共需五个步骤,请你根据顺序将下列五个步骤重新排序 。(1)过D作DE垂直BF,
(2)在BF上,取C、D两点,
使BC=CD,
(3)使A、C、E三点共线
(4)过B作BF垂直AB,
(5)量出DE的长,就是河
的宽,2、如图是挂在墙上的一面大镜子,上面有两点A、B。小明想知道A、B两点之间的距离,但镜子挂得太高,无法直接测量,旁边又没有梯子,只有一根长度比圆的直径稍长点的竹竿和一把卷尺。小明做了如下操作:在他够的着的圆上找到一点C ,接下去小明却忘了应该怎么做?你能帮助他完成吗?A ·· BEDC●3、要测量圆形工件的外径,工人师傅设计了如图所示的卡钳,O为卡钳两柄交点,且有OA=OB=OC=OD,如果圆形工件恰好通过卡钳AB,则次工件的外径必是CD之长了,你能说明其中的道理吗?1、课间,小明拿着老师的等腰三角板玩,不小心掉到两墙之间,如图,
求证:△ADC≌△CEB.2.如图有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,把△ABC折叠,
使点B与点A重合,折痕为DE,则△ACD的周长为( )
(2)能从实例中构建全等三角形,用以解决问题。学习目标 (1分钟)1.判断两个三角形全等的条件有:(1): ;(2): ;(3): ;SSSASAAAS复习回顾(1分钟)(4): ;SAS2.全等三角形的性质是 .?全等三角形的对应边相等?全等三角形的对应角相等HL如图,已知∠1=∠2,AC=AD,增加下列条件:
①AB=AE;②BC=ED;③∠C=∠D;④∠B=∠E,其中能使△ABC≌△AED的条件有( )
A.4个 B.3个 C.2个 D.1个复习检测(2分钟)B下面是一位经历过战争的老人讲述的一个故事: 在一次战役中,我军阵地与敌军碉堡隔河相望.为了炸掉这个碉堡,需要知道碉堡与我军阵地的距离.在不能过河测量又没有任何测量工具的情况下,如何估测这个距离呢?探究:利用三角形全等测距离 他面向碉堡的方向站好,然后调整帽子,使视线通过帽檐正好落在碉堡的底部;
然后,他转过一个角度,保持刚才的姿态,这时视线落在了自己所在岸的某一点上;
接着,他用步测的办法量出自己与那个点的距离,这个距离就是他与碉堡间的距离.这位聪明的八路军战士的方法如下:阅读相关内容完成下列问题:
(1)在引例中,“保持刚才的姿态”你是怎样理解的?
答:___________________.
(2)直立的姿态从而保证了两个三角形中的两个_____;帽檐不动,保证了视线和身体的_____不变.
(3)要说明图中两个三角形全等,已知两角,则还差一边,即_________.
(4)测量的原理是:构造了_______________.直立姿态和帽檐不动直角夹角身高不变两个全等三角形构造全等三角形自学指导(一)(5分钟)
阅读课本108页的内容,思考如下问题:1、战士的方法是根据什么?2、构建出全等三角形中,已知条件是什么?
结论又是什么?3、你能用所学习的知识解释其中的道理吗?ABCDEF∠B= ∠EBC=EF∠C= ∠ F△ABC≌△DEFAB=DE利用三角形全等测距离的实质是什么?
其实质为构造三角形全等,
根据全等三角形对应边相等,
将不可测的线段的长度,
转化为可测线段长度.1.如图所示小明设计了一种测工件内径AB的卡钳,问:在卡钳的设计中,AO、BO、CO、DO 应满足下列的哪个条件?( )
A、AO=CO
B、BO=DO
C、AC=BD
D、AO=CO且BO=DOD自学检测(一) (4分钟)2、如图,工人师傅要计算一个圆柱形容器的容积,需要测量其内径。现在有两根同样长的木棒、一条橡皮绳和一把带有刻度的直尺,你能想法帮助他完成吗?·中点CAB先在地上取一个可以直接到达 A 点和B点的点C,连接 AC 并延长到 D,使CD= CA;连接BC并延长到E,使CE= CB,连接DE并测量出它的长度,DE的长度就是 A,B 间的距离.BA·CDE····P108 想一想: 如图,A,B 两点分别位于一个池塘的两端,小明想用绳子测量 A,B 间的距离,但绳子不够长,一个叔叔帮他出了这样一个主意:BA··CDE···自学指导(二)(6+3分钟)
阅读课本108页“想一想” 思考如下问题;
1、仿照指导(一)的方法,构建三角形,并写出“已
知”、“求证”的内容。已知:CA=CD,CB=CE, ∠ACB= ∠ DCE
求证:AB=DE。2、你能设计出其它的方案来吗?(构建全等三角形)3、已知条件是什么?结论又是什么?4、你能说明设计出方案的理由吗?BA·····CED如图,已知AB⊥BF,DG⊥BF,BC=DC,
求证:AB=DE。FG1、如图要测量河两岸相对的两点A、B的距离,先在AB 的垂线BF上取两点C、D,使CD=CB,再定出BF的垂线DE,可以证明△EDC≌△ABC,得ED=AB,因此,测得ED的长就是AB的长。判定△EDC≌△ABC的理由是( )
A、SSS B、ASA C、AAS D、SASB自学检测(二)(5+2分钟)2、如图,山脚下有A、B两点,要测出A、B两点的距离。 (1)在地上取一个可以直接到达A、B点的点O,连接AO并延长AO到C,使AO=CO,你能完成剩下的图形吗?(2)说明你是如何求AB的距离。??解:在△AOB与△COD中,AO = CO∠ AOB = ∠CODBO = DO∴△AOB≌△ COD(SAS)∴ AB=CD (全等三角形的对应边相等)即:通过测量C、D之间的距离可以求A、B的距离(已知)(对顶角相等)(已知)选择恰当的判断条件构造全等三角形说明理由(证明 )下结论方法点拨:当堂训练(10分钟)1.如图,A、B、C、D是四个村庄,B、C、D在一条东西 走向公路的沿线上,BD=1千米,DC=1千米,村AC、AD间也有公路相连且AC=3千米,只有AB之间由于间隔了一个小湖,所以无直接相连的公路,现决定在湖面上造一座斜拉桥,测得AE=1.2千米,BF=0.7千米,则斜拉桥长至少有 千米D1.12.如图,公园里有一条“z”字形道路ABCD,其中AB∥CD,在AB、BC、CD三段路旁各有一只小凳E、M、F,M恰为BC的中点,且E、F、M在同一条直线上,在BE道路上停放着一排小汽车,从而无法直接测量B、E之间的距离,你能想出解决的办法吗?试说明理由。ACBDEMF在△EMB和△FMC中,∠ B = ∠C∴△ EMB ≌△ FMC (ASA)∴ EB=FC (全等三角形的对应边相等)(已证)(已证)BM = CM ∠ EMB = ∠FMC(对顶角相等)解:如图所示,连接E、M、F
∵AB∥CD
∴∠B=∠C ( 两直线平行,
内错角相等 )
∵ M是BC的中点,
∴BM=CM (中点的定义)即:通过测量F、C之间的距离可以求E、B的距离ACBDEMF1、如图,要量河两岸相对两点A、B的距离。
下图是一位同学利用三角形全等所画的图,共需五个步骤,请你根据顺序将下列五个步骤重新排序 。(1)过D作DE垂直BF,
(2)在BF上,取C、D两点,
使BC=CD,
(3)使A、C、E三点共线
(4)过B作BF垂直AB,
(5)量出DE的长,就是河
的宽,2、如图是挂在墙上的一面大镜子,上面有两点A、B。小明想知道A、B两点之间的距离,但镜子挂得太高,无法直接测量,旁边又没有梯子,只有一根长度比圆的直径稍长点的竹竿和一把卷尺。小明做了如下操作:在他够的着的圆上找到一点C ,接下去小明却忘了应该怎么做?你能帮助他完成吗?A ·· BEDC●3、要测量圆形工件的外径,工人师傅设计了如图所示的卡钳,O为卡钳两柄交点,且有OA=OB=OC=OD,如果圆形工件恰好通过卡钳AB,则次工件的外径必是CD之长了,你能说明其中的道理吗?1、课间,小明拿着老师的等腰三角板玩,不小心掉到两墙之间,如图,
求证:△ADC≌△CEB.2.如图有一张直角三角形纸片,两直角边AC=5cm,BC=10cm,把△ABC折叠,
使点B与点A重合,折痕为DE,则△ACD的周长为( )
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
