名校物理之高考专题六 电路的分析问题
图片预览


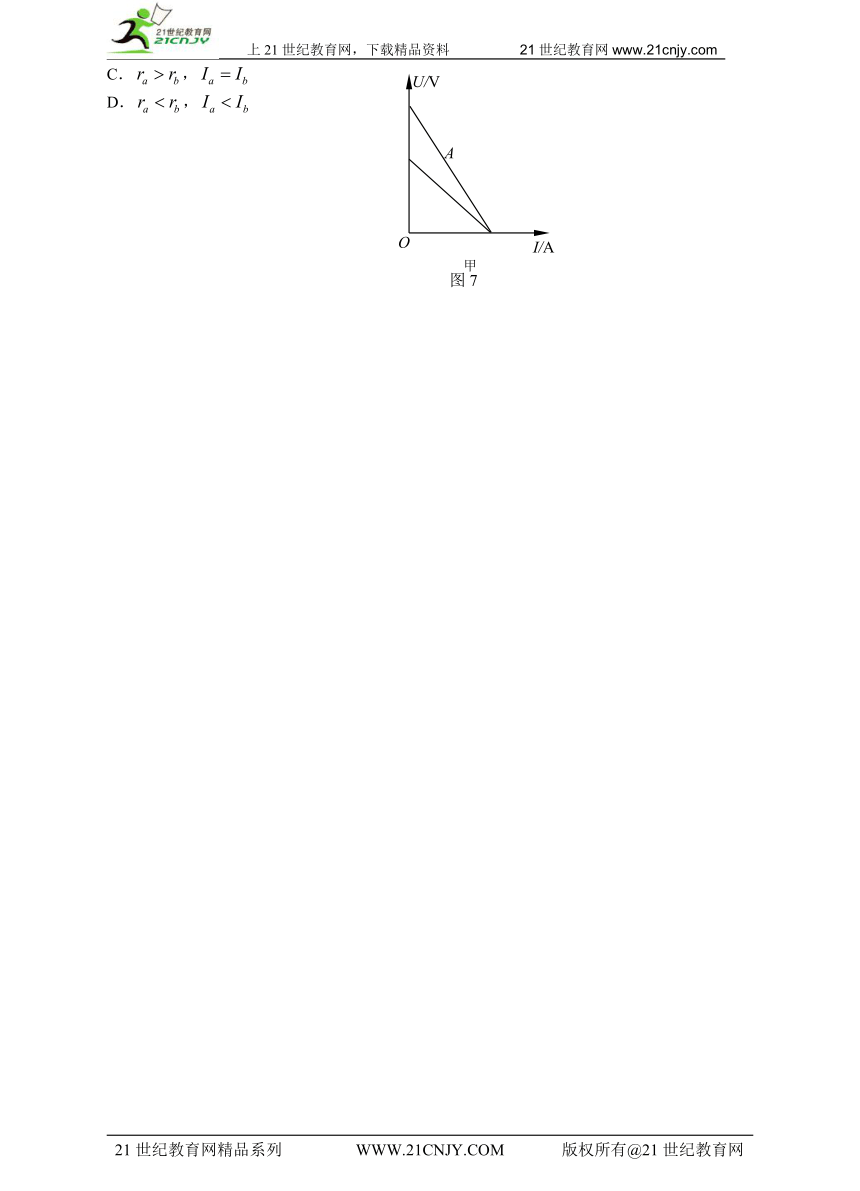
文档简介
上21世纪教育网,下载精品资料 21世纪教育网www.21cnjy.com
专题六 电路的分析问题(1课时)
【考纲要求】
内 容 要求 说 明
电流 电动势 电阻定律 电阻的串联与并联 Ⅰ
电功 电功率 焦耳定律 简单的逻辑电路 Ⅰ 逻辑电路设计和定量计算不作要求
欧姆定律 闭合电路欧姆定律 Ⅱ
【重点知识梳理】
1. 的定向移动形成电流。通过导体横截面积的电荷量q跟通过这些电荷量所用时间t的比值称为电流,则有I= 。导线中的电场线保持与导线平行。电动势是描述电源把其他形式的能转化为电能本领强弱的物理量,在数值上等于非静电力把1C的正电荷在电源内从负极送到正极所做的功的大小。E= ,其值也等于电源没有接入外电路时两极间的电压。
2.电阻定律:导体的电阻R跟它的长度L成 ,跟它的横截面积S成 。写成公式,则有 。此式中的比例常数是 ,它与 、 有关。
3.部分电路欧姆定律:导体中的电流I跟导体两端的电压U成 ,跟导体的电阻成 。写成公式 。其适用条件是 。
4.电功公式W= 。电热公式Q= 。在纯电阻电路中,W Q,在非纯电阻电路中,W Q。电功率公式P= 。热功率公式P= 。
5.闭合电路欧姆定律
(1)内容:闭合电路中的电流,跟电源的电动势成 ,跟整个电路的电阻成 。
(2)公式 或 。
(3)路端电压的关系式 。R增大,I ,当R→∞(断路)时,I ;R减小,I ,当R=0(短路),I 。
6.电源的有关功率和电源的效率:(1)电源的总功率P总= ;(2)电源的输出功率P出= ;(3)电源的内部发热功率P热= ;(4)电源的效率= 。
7.简单的逻辑电路
(1)“与”门电路: 。其电路符号 。
(2)“或”门电路: 。其电路符号 。
(3)“非”门电路: 。其电路符号 。
【分类典型例题】
题型一:直流电路的动态分析
解决这类问题需要注意:按局部(R的变化)→全局(I总、U端的变化)→局部(U分、I分的变化)的逻辑思维进行分析推理。
[例1]在如图1所示的电路中,滑动变阻器的滑动触点向b端移动时( )
A.电压表V的读数增大,电流表A的读数减小
B.电压表V和电流表A的读数都增大
C.电压表V和电流表A的读数都减小
D.电压表V的读数减小,电流表A的读数增大
[解析]滑动变阻器的滑动触点向b端移动时,R3接入电路中的阻值变大,使得I总减小,内电压减小,由U=E-Ir得外电压U外增大,即电压表读数增大。电阻R1中的电流减小,电压减小,电阻R2两端的电压(U2=U外-U1)增大,电流也增大,电阻R3中的电流(I3=I总- I2)减小,即电流表读数减小。答案:A。
[变式训练1]在图2所示的电路中,观察三只小灯泡亮度变化和两只电压表变化情况,如果滑动变阻器的滑片P由a端滑至b端,电压表V1示数变化的绝对值为△U1,电压表V2示数变化的绝对值为△U2,则下列说法正确的有( )
A.L1、L3变暗,L2变亮
B.L3变暗,L1、L2变亮
C.△U1﹤△U2
D.△U1﹥△U2
2.如图3所示电路中,由于某一电阻发生短路或断路,使A灯变暗,
B灯变亮,则故障可能是( )
A.R1短路 B.R2断路 C.R3断路 D.R4短路
题型二:电路中的能量转化
解决这类问题需要注意:一是能量转化的方向问题;二是能量转化量的计算问题。
[例2]环保汽车将为2008年奥运会场馆服务。某辆以蓄电池为驱动能源的环保汽车,总质量=3×103kg。当它在水平路面上以=36km/h的速度匀速行驶时,驱动电机的输入电流=50A,电压=300V。在此行驶状态下,求:
(1)驱动电机的输入功率P电。
(2)若驱动电机能够将输入功率的90%转化为用于牵引汽车前进的机械功率P机,求汽车所受阻力与车重的比值。(取10m/s2)
(3)设想改用太阳能电池给该车供电,其它条件不变,求所需太阳能电池板的最小面积。
已知太阳辐射的总功率P0=4×1026W,太阳到地球的距离r=1.5×1011m,太阳光传播到达地面的过程中大约有30%的能量损耗,该车所用太阳能电池的能量转化效率约为15%。
[解析](1)驱动电机的输入功率==1.5×104W。
(2)在匀速行驶时=0.9==,=
汽车所受阻力与车重之比=0.045。
(3)当太阳垂直电池板入射时,所需电池板面积最小,设其为,距太阳中心为的球面面积=πr2
若没有能量损耗,太阳能电池板接受到的太阳能功率为,则=,
设太阳能电池板实际接收到的太阳能功率为,则=(1-30%)所以,由于=15%,所以电池板的最小面积==101m2。
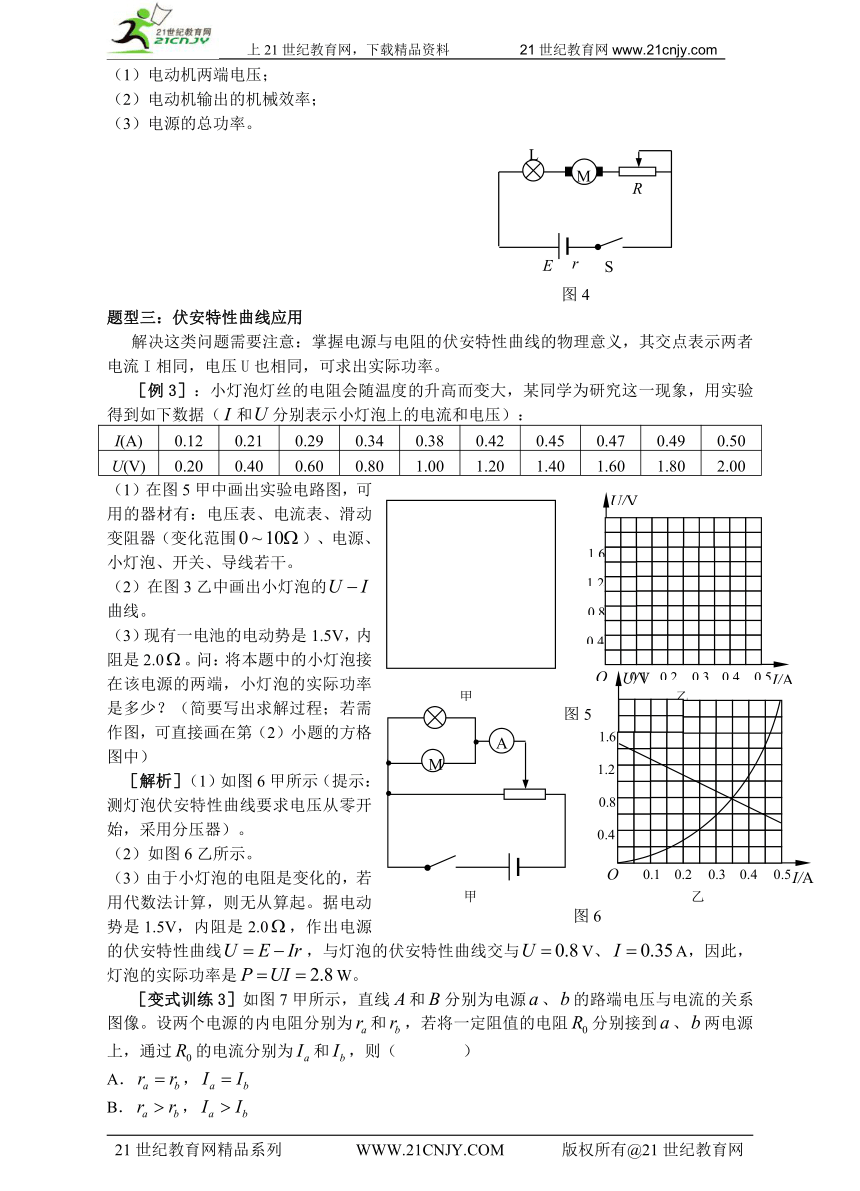
[变式训练2]如图4所示,电源电动势=14V,内阻=1欧,小灯泡L标有“2V,4W”,电动机的内阻=0.5欧,当变阻器调到=1欧时,电灯和电动机正常工作。求:
(1)电动机两端电压;
(2)电动机输出的机械效率;
(3)电源的总功率。
题型三:伏安特性曲线应用
解决这类问题需要注意:掌握电源与电阻的伏安特性曲线的物理意义,其交点表示两者电流I相同,电压U也相同,可求出实际功率。
[例3]:小灯泡灯丝的电阻会随温度的升高而变大,某同学为研究这一现象,用实验得到如下数据(和分别表示小灯泡上的电流和电压):
I(A) 0.12 0.21 0.29 0.34 0.38 0.42 0.45 0.47 0.49 0.50
U(V) 0.20 0.40 0.60 0.80 1.00 1.20 1.40 1.60 1.80 2.00
(1)在图5甲中画出实验电路图,可用的器材有:电压表、电流表、滑动变阻器(变化范围)、电源、小灯泡、开关、导线若干。
(2)在图3乙中画出小灯泡的曲线。
(3)现有一电池的电动势是1.5V,内阻是2.0。问:将本题中的小灯泡接在该电源的两端,小灯泡的实际功率是多少?(简要写出求解过程;若需作图,可直接画在第(2)小题的方格图中)
[解析](1)如图6甲所示(提示:测灯泡伏安特性曲线要求电压从零开始,采用分压器)。
(2)如图6乙所示。
(3)由于小灯泡的电阻是变化的,若用代数法计算,则无从算起。据电动势是1.5V,内阻是2.0,作出电源的伏安特性曲线,与灯泡的伏安特性曲线交与V、A,因此,灯泡的实际功率是W。
[变式训练3]如图7甲所示,直线和分别为电源、的路端电压与电流的关系图像。设两个电源的内电阻分别为和,若将一定阻值的电阻分别接到、两电源上,通过的电流分别为和,则( )
A.,
B.,
C.,
D.,
【能力训练】
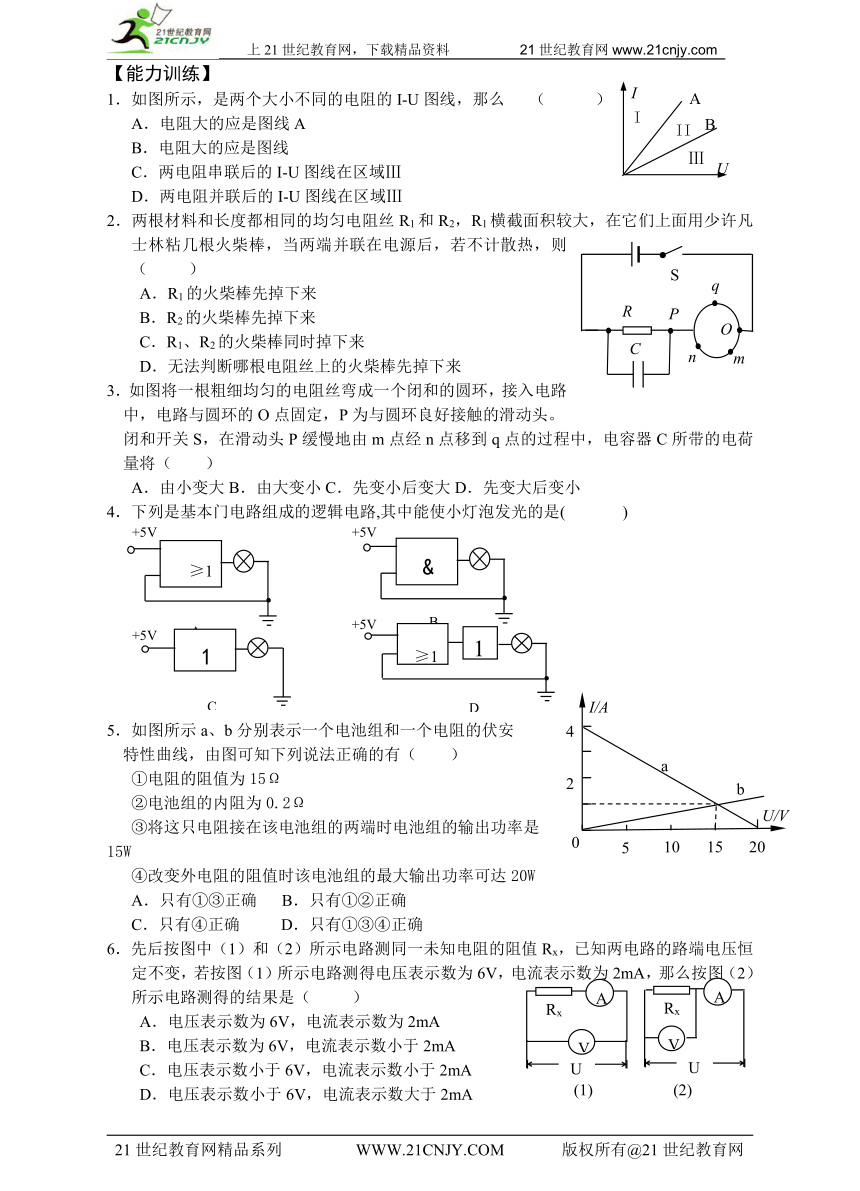
1.如图所示,是两个大小不同的电阻的I-U图线,那么 ( )
A.电阻大的应是图线A
B.电阻大的应是图线
C.两电阻串联后的I-U图线在区域Ⅲ
D.两电阻并联后的I-U图线在区域Ⅲ
2.两根材料和长度都相同的均匀电阻丝R1和R2,R1横截面积较大,在它们上面用少许凡士林粘几根火柴棒,当两端并联在电源后,若不计散热,则( )
A.R1的火柴棒先掉下来
B.R2的火柴棒先掉下来
C.R1、R2的火柴棒同时掉下来
D.无法判断哪根电阻丝上的火柴棒先掉下来
3.如图将一根粗细均匀的电阻丝弯成一个闭和的圆环,接入电路
中,电路与圆环的O点固定,P为与圆环良好接触的滑动头。
闭和开关S,在滑动头P缓慢地由m点经n点移到q点的过程中,电容器C所带的电荷量将( )
A.由小变大B.由大变小C.先变小后变大D.先变大后变小
4.下列是基本门电路组成的逻辑电路,其中能使小灯泡发光的是( )
5.如图所示a、b分别表示一个电池组和一个电阻的伏安
特性曲线,由图可知下列说法正确的有( )
①电阻的阻值为15Ω
②电池组的内阻为0.2Ω
③将这只电阻接在该电池组的两端时电池组的输出功率是15W
④改变外电阻的阻值时该电池组的最大输出功率可达20W
A.只有①③正确 B.只有①②正确
C.只有④正确 D.只有①③④正确
6.先后按图中(1)和(2)所示电路测同一未知电阻的阻值Rx,已知两电路的路端电压恒定不变,若按图(1)所示电路测得电压表示数为6V,电流表示数为2mA,那么按图(2)所示电路测得的结果是( )
A.电压表示数为6V,电流表示数为2mA
B.电压表示数为6V,电流表示数小于2mA
C.电压表示数小于6V,电流表示数小于2mA
D.电压表示数小于6V,电流表示数大于2mA
7.如图所示,电源内阻不可忽略,已知R1为半导体热敏电阻,R2为锰铜合金制成的可变电阻,当发现灯泡的亮度逐渐变暗时,可能的原因是( )
A.R1的温度逐渐降低
B.R1受到的可见光的照射
C.R2的阻值逐渐增大
D.R2的阻值逐渐减小
8.经过精确校准的电压表V1和V2,分别用来测量某线路中电阻R两端a、b间的电压时,如图所示,读数依次为12.7V和12.3V,则( )
A.a、b间的实际电压略大于12.7V
B.a、b间的实际电压略小于12.7V
C.电压表V1的内阻大于电压表V2的内阻
D.电压表V1的内阻小于电压表V2的内阻
9.如图所示电路,闭合开关时灯不亮,已经确定是灯泡断路或短路引
起的,在不能拆开电路的情况下(开关可闭合,可断开),现用一个
多用电表的直流电压档、直流电流档和欧姆档分别对故障作出如下
判断(如表所示)
次序 操作步骤 现象和结论
1 闭合开关,选直流电压档,红黑表笔分别接a、b 有示数,灯断路,无示数,灯短路
2 闭合开关,选直流电流档,红黑表笔分别接a、b 有示数,灯断路,无示数,灯短路
3 闭合开关,选欧姆档,红黑表笔分别接a、b 指针不动,灯断路,指针偏转,灯短路
4 断开开关,选欧姆档,红黑表笔分别接a、b 指针不动,灯断路,指针偏转,灯短路
以上判断正确的是( )
A.只有1、2对 B.只有3、4对 C.只有1、2、4对 D.全对
10.某居民家中的电路如图所示,开始时各部分均正常工作,将电饭煲的插头插入三孔插座后,正在烧水的电壶突然不能工作,但电灯仍然正常发光,拔出电饭煲的插头
(1)把试电笔分别插入插座的左、右插孔,氖管均能发光,则( )
A.仅电热壶所在的C、B两点间发生了断路故障
B.仅电热壶所在的C、B两点间发生了短路故障
C.仅导线A、B断路
D.因插座用导线接地,所以发生了上述故障
(2)用电压表测得A、B间电压Uab=0,测得C、B间电压
Ubc=220V,则电路故障是上述选项中的 。
11.电热毯、电饭锅等是人们常用的电热式家用电器,他们 一
般具有加热和保温功能,其工作原理大致相同。图①为某种电热式电器的简化电路图,主要元件有电阻丝R1、R2和自动开关
(1)当自动开关S闭合和断开时,用电器分别处于什么状态?
(2)用电器由照明电路供电(U=220V ),设加热时用电器的电功率为400W,保温时用电器的电功率为40W,则R1和R2分别为多大?
(3)若将图①中的自动开关S换成理想的晶体二极管D,如图②所示,其他条件不变,求该用电器工作1小时消耗的电能。
12.一辆电动自行车的铭牌上给出了如下表的技术参数:
规格 后轮驱动直流永磁毂电机
车型 26//电动自行车 额定输出功率 120W
整车质量 30kg 额定电压 40V
最大载重 120 kg 额定电流 3.5A
质量为M=70kg的人骑此电动自行车沿平直公路行驶,所受阻力f恒为车和人总重的k=0.02倍。取g=10m/s2,求:
(1)此车的永磁毂电机在额定电压下正常工作的效率;
(2)仅在永磁毂电机以额定功率提供动力的情况下,人骑车行驶的最大速度。
专题六参考答案:
[变式训练]:解析:小球离开锥面前,,其中,θ表示悬线与竖直方向的夹角,L表示摆长。小球离开锥面后,。可知C项正确。
答案:C。
题后反思:本题涉及到圆锥摆运动模型,要求考生通过受力分析和临界分析,抓住向心力的变化情况,从而顺利求解。
1.C(小球做平抛运动,由可确定A选项;由可确定B选项;由可确定D选项。不能确定的是C选项)。
2.C(据物体做直线运动的条件知,探测器加速直线运动时所受重力和推力的合力应沿倾斜直线,故喷气方向应偏离直线向后下方;探测器匀速运动时,探测器所受合力为零,探测器通过喷气而获得推动力应竖直向上,故喷气方向应竖直向下。故正确答案为C)
3.C(对小球进行受力分析,小球受到两个作用力,即重力和杆对小球的作用力,两个力的合力提供向心力,根据牛顿第二定律就可得C正确。)
4.D 国际空间站绕地球作圆周运动, 处于失重状态. 水银气压计利用空气压力与水银柱重力平衡测定气压, 故水银气压计无法使用; 天平利用两侧重力平衡测定质量, 故天平无法使用; 摆钟摆动的动力为重力, 故摆钟无法使用; 多用电表与重力无关, 故仍可使用。
5.AB(可得土星对土卫六的万有引力更大;有开普勒定律得:,可知土卫五的公转周期更小;根据可知土卫五的公转角速度大;根据土卫五的公转线速度大。)
6.D 万有引力提供向心力,由牛顿第二定律得,可以确定,离太阳越远向心加速度和线速度都越小,故AB都不正确;由题干提供的信息“这是6万年来火星距地球最近的一次”,可知C选项不正确。故正确答案为D。
7.C (由可知,C正确)
8.AD (由知,A正确;由,因两颗天体半径R不确定,故B不正确。由知,C不正确;由得D正确。故选AD)
9.AD(若该环是土星的一部分,由v=Rω,则v∝R;若该环是土星的卫星群,由GMm/R2=mv2/R,则v2∝1/R。故选项AD 正确。)
10.AD(如果万有引力不足以充当向心力,星球就会解体,据万有引力定律和牛顿第二定律得:GR 得T=2π,又因为M=πρR3,所以T=)
11.CD(本题考查学生对第一宇宙速度的理解,以及对卫星能沿椭圆轨道运动条件的理解。本题极易错选A)
12.①;②6.8rad/s(6.75~6.84都对)
13.解析:机车拐弯处视为圆周运动,此时向心力是由火车的重力和轨道对火车的支持力来提供的,如图所示。设轨道与水平面的夹角为,则
由向心力公式和几何关系可得:
,
解得:
14.解:(1)汽车在水平路面上拐弯,可视为汽车做匀速圆周运动,其向心力是车与路面间的静摩擦力提供,当静摩擦力达到最大值时,由向心力公式可知这时的半径最小,有
Fm=0.6mg≥
由速度v=30m/s,得弯道半径 r≥150m;
(2)汽车过拱桥,看作在竖直平面内做匀速圆周运动,到达最高点时,根据向心力公式有:mg-FN=
为了保证安全,车对路面间的弹力FN必须大于等于零。有 mg≥
则R≥90m。
15.解:(1)由题意可知:小球落到斜面上并沿斜面下滑,说明此时小球速度方向与斜面平行,否则小球会弹起,所以vy = v0tan53°
vy2 = 2gh
代入数据,得vy = 4m/s,v0 = 3m/s
(2)由vy = gt1得t1 = 0.4s
s =v0t1 = 3×0.4m = 1.2m
(3)小球沿斜面做匀加速直线运动的加速度a =
初速度 = 5m/s
=vt2 + a t22
代入数据,整理得 4t22 + 5t2 - 26 = 0
解得 t2 = 2s 或t2 = s(不合题意舍去)
所以t = t1 + t2 = 2.4s
16.解析: (1)把滑雪爱好者着地时的速度vt分解为如图所示的v0、vy两个分量
由
解得t=0.5s
则 vy=gt=5m/s
又vy=v0tan45°
解得 v0=5m/s
着地点到平台边缘的水平距离:x= v0t=2.5m
(2)滑雪者在平台上滑动时,受到滑动摩擦力作用而减速运动,由动能定理得
解得:v=7m/s
即滑雪者的初速度为7m/s。
17。解:(1)物体的水平位移相同,说明物体离开B点的速度相同,物体的速度大于皮带的速度,一直做匀减速运动。
(2)当ω=10rad/s时,物体经过B点的速度为m/s ①
平抛运动: ②
③
解得:t=1s,h=5m ④
(3)当ω>30rad/s时,水平位移不变,说明物体在AB之间一直加速,其末速度
m/s ⑤
根据 ⑥
当0≤ω≤10rad/s时, ⑦
当ω≥30rad/s时, ⑧
解得: ⑨
题后反思:本题以传送带上物体的运动为背景,涉及到直线运动、牛顿定律、圆周运动、平抛运动等较多知识点,过程多,情景复杂,对考生综合应用能力要求较高。
18.解:(1)由动能定理得,由远地点到近地点万有引力所做的功
①
(2)在近地点,由牛顿第二定律得 ②
在远地点有 ③
由以上两式得 ④
19.解析:设“卡西尼”号的质量为m,土星的质量为M. “卡西尼”号围绕土星的中心做匀速圆周运动,其向心力由万有引力提供.
由题意
所以:.
又
得
20.解:(1)对宇航员进行受力分析,并由牛顿第二定律得
N=5mg,
对火箭应用牛顿第二定律得
由以上两式解得 N
(2)飞船运行周期1.5 h,轨道半径为r1,同步卫星运行周期为T2=24 h,轨道半径为r2,对飞船及同步卫星分别有
解得
代入数据解得
21.解:设中央恒星质量为M,A行星质量为m,则由万有引力定律和牛顿第二定律得 ①
解得 ②
(2)由题意可知,A、B相距最近时,B对A的影响最大,且每隔t0时间相距最近。
设B行星周期为TB,则有: ③
解得: ④
设B行星的质量为mB,运动的轨道半径为RB,则有
⑤
由①④⑤得: ⑥
0.4
0.3
0.2
0.1
I/A
U/V
图6
图5
甲
乙
O
1.6
1.2
0.8
0.4
0.5
0.4
0.3
0.2
0.1
I/A
U/V
M
图4
r
E
R
S
L
图3
R4
r
E
R3
R2
R1
B
A
E r
V2
图2
b
a
P
L2
L3
L1
V1
图1
R3
R1
R2
a
r
E
V
A
b
0.5
0.4
0.8
1.2
1.6
O
乙
甲
A
A
M
O
A
I/A
U/V
甲
图7
I
U
A
B
II
Ⅲ
I
R
C
P
q
n
m
S
O
≥1
A
+5V
&
B
+5V
1
C
+5V
1
≥1
D
+5V
U/V
I/A
0
2
4
10
5
15
20
a
b
A
V
Rx
U
A
V
Rx
U
(1)
(2)
L
R1
R2
V
U
R0
R
a
b
L1
R
S
a
b
电壶
220V
火线
零线
左孔
右孔
C
B
A
图②
D
R2
R1
~
S
R2
R1
~
图①
υ0
h
53°
s
υ0
υy
υ
21世纪教育网精品系列 WWW.21CNJY.COM 版权所有@21世纪教育网
专题六 电路的分析问题(1课时)
【考纲要求】
内 容 要求 说 明
电流 电动势 电阻定律 电阻的串联与并联 Ⅰ
电功 电功率 焦耳定律 简单的逻辑电路 Ⅰ 逻辑电路设计和定量计算不作要求
欧姆定律 闭合电路欧姆定律 Ⅱ
【重点知识梳理】
1. 的定向移动形成电流。通过导体横截面积的电荷量q跟通过这些电荷量所用时间t的比值称为电流,则有I= 。导线中的电场线保持与导线平行。电动势是描述电源把其他形式的能转化为电能本领强弱的物理量,在数值上等于非静电力把1C的正电荷在电源内从负极送到正极所做的功的大小。E= ,其值也等于电源没有接入外电路时两极间的电压。
2.电阻定律:导体的电阻R跟它的长度L成 ,跟它的横截面积S成 。写成公式,则有 。此式中的比例常数是 ,它与 、 有关。
3.部分电路欧姆定律:导体中的电流I跟导体两端的电压U成 ,跟导体的电阻成 。写成公式 。其适用条件是 。
4.电功公式W= 。电热公式Q= 。在纯电阻电路中,W Q,在非纯电阻电路中,W Q。电功率公式P= 。热功率公式P= 。
5.闭合电路欧姆定律
(1)内容:闭合电路中的电流,跟电源的电动势成 ,跟整个电路的电阻成 。
(2)公式 或 。
(3)路端电压的关系式 。R增大,I ,当R→∞(断路)时,I ;R减小,I ,当R=0(短路),I 。
6.电源的有关功率和电源的效率:(1)电源的总功率P总= ;(2)电源的输出功率P出= ;(3)电源的内部发热功率P热= ;(4)电源的效率= 。
7.简单的逻辑电路
(1)“与”门电路: 。其电路符号 。
(2)“或”门电路: 。其电路符号 。
(3)“非”门电路: 。其电路符号 。
【分类典型例题】
题型一:直流电路的动态分析
解决这类问题需要注意:按局部(R的变化)→全局(I总、U端的变化)→局部(U分、I分的变化)的逻辑思维进行分析推理。
[例1]在如图1所示的电路中,滑动变阻器的滑动触点向b端移动时( )
A.电压表V的读数增大,电流表A的读数减小
B.电压表V和电流表A的读数都增大
C.电压表V和电流表A的读数都减小
D.电压表V的读数减小,电流表A的读数增大
[解析]滑动变阻器的滑动触点向b端移动时,R3接入电路中的阻值变大,使得I总减小,内电压减小,由U=E-Ir得外电压U外增大,即电压表读数增大。电阻R1中的电流减小,电压减小,电阻R2两端的电压(U2=U外-U1)增大,电流也增大,电阻R3中的电流(I3=I总- I2)减小,即电流表读数减小。答案:A。
[变式训练1]在图2所示的电路中,观察三只小灯泡亮度变化和两只电压表变化情况,如果滑动变阻器的滑片P由a端滑至b端,电压表V1示数变化的绝对值为△U1,电压表V2示数变化的绝对值为△U2,则下列说法正确的有( )
A.L1、L3变暗,L2变亮
B.L3变暗,L1、L2变亮
C.△U1﹤△U2
D.△U1﹥△U2
2.如图3所示电路中,由于某一电阻发生短路或断路,使A灯变暗,
B灯变亮,则故障可能是( )
A.R1短路 B.R2断路 C.R3断路 D.R4短路
题型二:电路中的能量转化
解决这类问题需要注意:一是能量转化的方向问题;二是能量转化量的计算问题。
[例2]环保汽车将为2008年奥运会场馆服务。某辆以蓄电池为驱动能源的环保汽车,总质量=3×103kg。当它在水平路面上以=36km/h的速度匀速行驶时,驱动电机的输入电流=50A,电压=300V。在此行驶状态下,求:
(1)驱动电机的输入功率P电。
(2)若驱动电机能够将输入功率的90%转化为用于牵引汽车前进的机械功率P机,求汽车所受阻力与车重的比值。(取10m/s2)
(3)设想改用太阳能电池给该车供电,其它条件不变,求所需太阳能电池板的最小面积。
已知太阳辐射的总功率P0=4×1026W,太阳到地球的距离r=1.5×1011m,太阳光传播到达地面的过程中大约有30%的能量损耗,该车所用太阳能电池的能量转化效率约为15%。
[解析](1)驱动电机的输入功率==1.5×104W。
(2)在匀速行驶时=0.9==,=
汽车所受阻力与车重之比=0.045。
(3)当太阳垂直电池板入射时,所需电池板面积最小,设其为,距太阳中心为的球面面积=πr2
若没有能量损耗,太阳能电池板接受到的太阳能功率为,则=,
设太阳能电池板实际接收到的太阳能功率为,则=(1-30%)所以,由于=15%,所以电池板的最小面积==101m2。
[变式训练2]如图4所示,电源电动势=14V,内阻=1欧,小灯泡L标有“2V,4W”,电动机的内阻=0.5欧,当变阻器调到=1欧时,电灯和电动机正常工作。求:
(1)电动机两端电压;
(2)电动机输出的机械效率;
(3)电源的总功率。
题型三:伏安特性曲线应用
解决这类问题需要注意:掌握电源与电阻的伏安特性曲线的物理意义,其交点表示两者电流I相同,电压U也相同,可求出实际功率。
[例3]:小灯泡灯丝的电阻会随温度的升高而变大,某同学为研究这一现象,用实验得到如下数据(和分别表示小灯泡上的电流和电压):
I(A) 0.12 0.21 0.29 0.34 0.38 0.42 0.45 0.47 0.49 0.50
U(V) 0.20 0.40 0.60 0.80 1.00 1.20 1.40 1.60 1.80 2.00
(1)在图5甲中画出实验电路图,可用的器材有:电压表、电流表、滑动变阻器(变化范围)、电源、小灯泡、开关、导线若干。
(2)在图3乙中画出小灯泡的曲线。
(3)现有一电池的电动势是1.5V,内阻是2.0。问:将本题中的小灯泡接在该电源的两端,小灯泡的实际功率是多少?(简要写出求解过程;若需作图,可直接画在第(2)小题的方格图中)
[解析](1)如图6甲所示(提示:测灯泡伏安特性曲线要求电压从零开始,采用分压器)。
(2)如图6乙所示。
(3)由于小灯泡的电阻是变化的,若用代数法计算,则无从算起。据电动势是1.5V,内阻是2.0,作出电源的伏安特性曲线,与灯泡的伏安特性曲线交与V、A,因此,灯泡的实际功率是W。
[变式训练3]如图7甲所示,直线和分别为电源、的路端电压与电流的关系图像。设两个电源的内电阻分别为和,若将一定阻值的电阻分别接到、两电源上,通过的电流分别为和,则( )
A.,
B.,
C.,
D.,
【能力训练】
1.如图所示,是两个大小不同的电阻的I-U图线,那么 ( )
A.电阻大的应是图线A
B.电阻大的应是图线
C.两电阻串联后的I-U图线在区域Ⅲ
D.两电阻并联后的I-U图线在区域Ⅲ
2.两根材料和长度都相同的均匀电阻丝R1和R2,R1横截面积较大,在它们上面用少许凡士林粘几根火柴棒,当两端并联在电源后,若不计散热,则( )
A.R1的火柴棒先掉下来
B.R2的火柴棒先掉下来
C.R1、R2的火柴棒同时掉下来
D.无法判断哪根电阻丝上的火柴棒先掉下来
3.如图将一根粗细均匀的电阻丝弯成一个闭和的圆环,接入电路
中,电路与圆环的O点固定,P为与圆环良好接触的滑动头。
闭和开关S,在滑动头P缓慢地由m点经n点移到q点的过程中,电容器C所带的电荷量将( )
A.由小变大B.由大变小C.先变小后变大D.先变大后变小
4.下列是基本门电路组成的逻辑电路,其中能使小灯泡发光的是( )
5.如图所示a、b分别表示一个电池组和一个电阻的伏安
特性曲线,由图可知下列说法正确的有( )
①电阻的阻值为15Ω
②电池组的内阻为0.2Ω
③将这只电阻接在该电池组的两端时电池组的输出功率是15W
④改变外电阻的阻值时该电池组的最大输出功率可达20W
A.只有①③正确 B.只有①②正确
C.只有④正确 D.只有①③④正确
6.先后按图中(1)和(2)所示电路测同一未知电阻的阻值Rx,已知两电路的路端电压恒定不变,若按图(1)所示电路测得电压表示数为6V,电流表示数为2mA,那么按图(2)所示电路测得的结果是( )
A.电压表示数为6V,电流表示数为2mA
B.电压表示数为6V,电流表示数小于2mA
C.电压表示数小于6V,电流表示数小于2mA
D.电压表示数小于6V,电流表示数大于2mA
7.如图所示,电源内阻不可忽略,已知R1为半导体热敏电阻,R2为锰铜合金制成的可变电阻,当发现灯泡的亮度逐渐变暗时,可能的原因是( )
A.R1的温度逐渐降低
B.R1受到的可见光的照射
C.R2的阻值逐渐增大
D.R2的阻值逐渐减小
8.经过精确校准的电压表V1和V2,分别用来测量某线路中电阻R两端a、b间的电压时,如图所示,读数依次为12.7V和12.3V,则( )
A.a、b间的实际电压略大于12.7V
B.a、b间的实际电压略小于12.7V
C.电压表V1的内阻大于电压表V2的内阻
D.电压表V1的内阻小于电压表V2的内阻
9.如图所示电路,闭合开关时灯不亮,已经确定是灯泡断路或短路引
起的,在不能拆开电路的情况下(开关可闭合,可断开),现用一个
多用电表的直流电压档、直流电流档和欧姆档分别对故障作出如下
判断(如表所示)
次序 操作步骤 现象和结论
1 闭合开关,选直流电压档,红黑表笔分别接a、b 有示数,灯断路,无示数,灯短路
2 闭合开关,选直流电流档,红黑表笔分别接a、b 有示数,灯断路,无示数,灯短路
3 闭合开关,选欧姆档,红黑表笔分别接a、b 指针不动,灯断路,指针偏转,灯短路
4 断开开关,选欧姆档,红黑表笔分别接a、b 指针不动,灯断路,指针偏转,灯短路
以上判断正确的是( )
A.只有1、2对 B.只有3、4对 C.只有1、2、4对 D.全对
10.某居民家中的电路如图所示,开始时各部分均正常工作,将电饭煲的插头插入三孔插座后,正在烧水的电壶突然不能工作,但电灯仍然正常发光,拔出电饭煲的插头
(1)把试电笔分别插入插座的左、右插孔,氖管均能发光,则( )
A.仅电热壶所在的C、B两点间发生了断路故障
B.仅电热壶所在的C、B两点间发生了短路故障
C.仅导线A、B断路
D.因插座用导线接地,所以发生了上述故障
(2)用电压表测得A、B间电压Uab=0,测得C、B间电压
Ubc=220V,则电路故障是上述选项中的 。
11.电热毯、电饭锅等是人们常用的电热式家用电器,他们 一
般具有加热和保温功能,其工作原理大致相同。图①为某种电热式电器的简化电路图,主要元件有电阻丝R1、R2和自动开关
(1)当自动开关S闭合和断开时,用电器分别处于什么状态?
(2)用电器由照明电路供电(U=220V ),设加热时用电器的电功率为400W,保温时用电器的电功率为40W,则R1和R2分别为多大?
(3)若将图①中的自动开关S换成理想的晶体二极管D,如图②所示,其他条件不变,求该用电器工作1小时消耗的电能。
12.一辆电动自行车的铭牌上给出了如下表的技术参数:
规格 后轮驱动直流永磁毂电机
车型 26//电动自行车 额定输出功率 120W
整车质量 30kg 额定电压 40V
最大载重 120 kg 额定电流 3.5A
质量为M=70kg的人骑此电动自行车沿平直公路行驶,所受阻力f恒为车和人总重的k=0.02倍。取g=10m/s2,求:
(1)此车的永磁毂电机在额定电压下正常工作的效率;
(2)仅在永磁毂电机以额定功率提供动力的情况下,人骑车行驶的最大速度。
专题六参考答案:
[变式训练]:解析:小球离开锥面前,,其中,θ表示悬线与竖直方向的夹角,L表示摆长。小球离开锥面后,。可知C项正确。
答案:C。
题后反思:本题涉及到圆锥摆运动模型,要求考生通过受力分析和临界分析,抓住向心力的变化情况,从而顺利求解。
1.C(小球做平抛运动,由可确定A选项;由可确定B选项;由可确定D选项。不能确定的是C选项)。
2.C(据物体做直线运动的条件知,探测器加速直线运动时所受重力和推力的合力应沿倾斜直线,故喷气方向应偏离直线向后下方;探测器匀速运动时,探测器所受合力为零,探测器通过喷气而获得推动力应竖直向上,故喷气方向应竖直向下。故正确答案为C)
3.C(对小球进行受力分析,小球受到两个作用力,即重力和杆对小球的作用力,两个力的合力提供向心力,根据牛顿第二定律就可得C正确。)
4.D 国际空间站绕地球作圆周运动, 处于失重状态. 水银气压计利用空气压力与水银柱重力平衡测定气压, 故水银气压计无法使用; 天平利用两侧重力平衡测定质量, 故天平无法使用; 摆钟摆动的动力为重力, 故摆钟无法使用; 多用电表与重力无关, 故仍可使用。
5.AB(可得土星对土卫六的万有引力更大;有开普勒定律得:,可知土卫五的公转周期更小;根据可知土卫五的公转角速度大;根据土卫五的公转线速度大。)
6.D 万有引力提供向心力,由牛顿第二定律得,可以确定,离太阳越远向心加速度和线速度都越小,故AB都不正确;由题干提供的信息“这是6万年来火星距地球最近的一次”,可知C选项不正确。故正确答案为D。
7.C (由可知,C正确)
8.AD (由知,A正确;由,因两颗天体半径R不确定,故B不正确。由知,C不正确;由得D正确。故选AD)
9.AD(若该环是土星的一部分,由v=Rω,则v∝R;若该环是土星的卫星群,由GMm/R2=mv2/R,则v2∝1/R。故选项AD 正确。)
10.AD(如果万有引力不足以充当向心力,星球就会解体,据万有引力定律和牛顿第二定律得:GR 得T=2π,又因为M=πρR3,所以T=)
11.CD(本题考查学生对第一宇宙速度的理解,以及对卫星能沿椭圆轨道运动条件的理解。本题极易错选A)
12.①;②6.8rad/s(6.75~6.84都对)
13.解析:机车拐弯处视为圆周运动,此时向心力是由火车的重力和轨道对火车的支持力来提供的,如图所示。设轨道与水平面的夹角为,则
由向心力公式和几何关系可得:
,
解得:
14.解:(1)汽车在水平路面上拐弯,可视为汽车做匀速圆周运动,其向心力是车与路面间的静摩擦力提供,当静摩擦力达到最大值时,由向心力公式可知这时的半径最小,有
Fm=0.6mg≥
由速度v=30m/s,得弯道半径 r≥150m;
(2)汽车过拱桥,看作在竖直平面内做匀速圆周运动,到达最高点时,根据向心力公式有:mg-FN=
为了保证安全,车对路面间的弹力FN必须大于等于零。有 mg≥
则R≥90m。
15.解:(1)由题意可知:小球落到斜面上并沿斜面下滑,说明此时小球速度方向与斜面平行,否则小球会弹起,所以vy = v0tan53°
vy2 = 2gh
代入数据,得vy = 4m/s,v0 = 3m/s
(2)由vy = gt1得t1 = 0.4s
s =v0t1 = 3×0.4m = 1.2m
(3)小球沿斜面做匀加速直线运动的加速度a =
初速度 = 5m/s
=vt2 + a t22
代入数据,整理得 4t22 + 5t2 - 26 = 0
解得 t2 = 2s 或t2 = s(不合题意舍去)
所以t = t1 + t2 = 2.4s
16.解析: (1)把滑雪爱好者着地时的速度vt分解为如图所示的v0、vy两个分量
由
解得t=0.5s
则 vy=gt=5m/s
又vy=v0tan45°
解得 v0=5m/s
着地点到平台边缘的水平距离:x= v0t=2.5m
(2)滑雪者在平台上滑动时,受到滑动摩擦力作用而减速运动,由动能定理得
解得:v=7m/s
即滑雪者的初速度为7m/s。
17。解:(1)物体的水平位移相同,说明物体离开B点的速度相同,物体的速度大于皮带的速度,一直做匀减速运动。
(2)当ω=10rad/s时,物体经过B点的速度为m/s ①
平抛运动: ②
③
解得:t=1s,h=5m ④
(3)当ω>30rad/s时,水平位移不变,说明物体在AB之间一直加速,其末速度
m/s ⑤
根据 ⑥
当0≤ω≤10rad/s时, ⑦
当ω≥30rad/s时, ⑧
解得: ⑨
题后反思:本题以传送带上物体的运动为背景,涉及到直线运动、牛顿定律、圆周运动、平抛运动等较多知识点,过程多,情景复杂,对考生综合应用能力要求较高。
18.解:(1)由动能定理得,由远地点到近地点万有引力所做的功
①
(2)在近地点,由牛顿第二定律得 ②
在远地点有 ③
由以上两式得 ④
19.解析:设“卡西尼”号的质量为m,土星的质量为M. “卡西尼”号围绕土星的中心做匀速圆周运动,其向心力由万有引力提供.
由题意
所以:.
又
得
20.解:(1)对宇航员进行受力分析,并由牛顿第二定律得
N=5mg,
对火箭应用牛顿第二定律得
由以上两式解得 N
(2)飞船运行周期1.5 h,轨道半径为r1,同步卫星运行周期为T2=24 h,轨道半径为r2,对飞船及同步卫星分别有
解得
代入数据解得
21.解:设中央恒星质量为M,A行星质量为m,则由万有引力定律和牛顿第二定律得 ①
解得 ②
(2)由题意可知,A、B相距最近时,B对A的影响最大,且每隔t0时间相距最近。
设B行星周期为TB,则有: ③
解得: ④
设B行星的质量为mB,运动的轨道半径为RB,则有
⑤
由①④⑤得: ⑥
0.4
0.3
0.2
0.1
I/A
U/V
图6
图5
甲
乙
O
1.6
1.2
0.8
0.4
0.5
0.4
0.3
0.2
0.1
I/A
U/V
M
图4
r
E
R
S
L
图3
R4
r
E
R3
R2
R1
B
A
E r
V2
图2
b
a
P
L2
L3
L1
V1
图1
R3
R1
R2
a
r
E
V
A
b
0.5
0.4
0.8
1.2
1.6
O
乙
甲
A
A
M
O
A
I/A
U/V
甲
图7
I
U
A
B
II
Ⅲ
I
R
C
P
q
n
m
S
O
≥1
A
+5V
&
B
+5V
1
C
+5V
1
≥1
D
+5V
U/V
I/A
0
2
4
10
5
15
20
a
b
A
V
Rx
U
A
V
Rx
U
(1)
(2)
L
R1
R2
V
U
R0
R
a
b
L1
R
S
a
b
电壶
220V
火线
零线
左孔
右孔
C
B
A
图②
D
R2
R1
~
S
R2
R1
~
图①
υ0
h
53°
s
υ0
υy
υ
21世纪教育网精品系列 WWW.21CNJY.COM 版权所有@21世纪教育网
同课章节目录
