通用版中考三轮冲刺复习动点综合问题(四)—函数中因动点产生的相似三角形问题
文档属性
| 名称 | 通用版中考三轮冲刺复习动点综合问题(四)—函数中因动点产生的相似三角形问题 |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-24 09:11:26 | ||
图片预览











文档简介
(共30张PPT)
动点综合问题(四)
通用版 中考复习
解读考点
知 识 点 名师点晴
动点问题中的特殊图形 等腰三角形与直角三角形 利用等腰三角形或直角三角形的特殊性质求解动点问题
相似问题 利用相似三角形的对应边成比例、对应角相等求解动点问题
动点问题中的计算问题 动点问题的最值与定值问题 理解最值或定值问题的求法
动点问题的面积问题 结合面积的计算方法来解决动点问题
动点问题的函数图象问题 一次函数或二次函数的图象 结合函数的图象解决动点问题
知识要点
专题四:函数中因动点产生的相似三角形问题
函数中因动点产生的相似三角形问题一般有三个解题途径:
① 求相似三角形的第三个顶点时,先要分析已知三角形的边和角的特点,进而得出已知三角形是否为特殊三角形。根据未知三角形中已知边与已知三角形的可能对应边分类讨论。
②或利用已知三角形中对应角,在未知三角形中利用勾股定理、三角函数、对称、旋转等知识来推导边的大小。
③若两个三角形的各边均未给出,则应先设所求点的坐标进而用函数解析式来表示各边的长度,之后利用相似来列方程求解。
典型例题
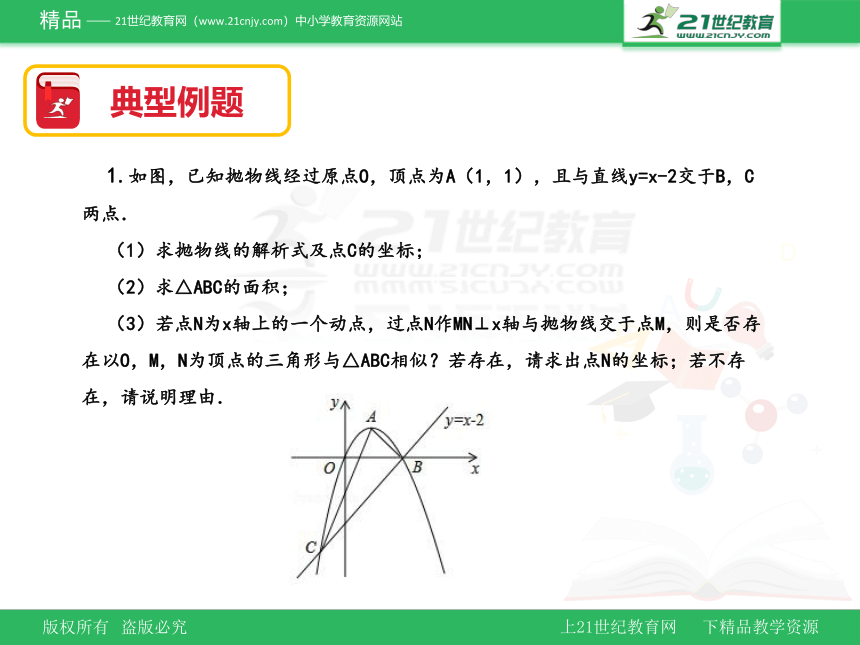
1.如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x-2交于B,C两点.
(1)求抛物线的解析式及点C的坐标;
(2)求△ABC的面积;
(3)若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由.
典型例题
解析:(1)可设顶点式,把原点坐标代入可求得抛物线解析式,联立直线与抛物线解析式,可求得C点坐标;
(2)设直线AC的解析式为y=kx+b,与x轴交于D,得到y=2x-1,求得
于是得到结论;
(3)设出N点坐标,可表示出M点坐标,从而可表示出MN、ON的长度,当△MON和△ABC相似时,利用三角形相似的性质可得
,可求得N点的坐标.
典型例题
解:(1)∵顶点坐标为(1,1),
∴设抛物线解析式为y=a(x-1) +1,
又抛物线过原点,
∴0=a(0-1) +1,解得a=-1,
∴抛物线解析式为y=-(x-1) +1,即y=-x +2x,
联立抛物线和直线解析式可得:
解得: ∴B(2,0),C(-1,-3);
典型例题
(2)设直线AC的解析式为y=kx+b,与x轴交于D,
把A(1,1),C(-1,-3)的坐标代入得
解得:
∴y=2x-1,当y=0,即2x-1=0,解得: x= 。
∴D( ,0)。
典型例题
(3)假设存在满足条件的点N,设N(x,0),则M(x,-x +2x),
∴ON=|x|,MN=|-x +2x|, 由(2)知,
∵MN⊥x轴于点N,∴∠ABC=∠MNO=90°,
∴当△ABC和△MNO相似时,
∵当x=0时M、O、N不能构成三角形,∴x≠0,
典型例题
即|x||-x+2|=3|x|,∴|-x+2|=3,
∴-x+2=±3,解得x=5或x=-1,
此时N点坐标为(-1,0)或(5,0),
综上可知存在满足条件的N点,其坐标或(-1,0)或(5,0).
典型例题
2.已知△ABC是边长为6cm的等边三角形,动点P、Q同时从B、A两点出发,分别沿BA、AC匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),解答下列问题:
(1)当t为何值时,AP=2AQ?
(2)当t为何值时,△APQ为直角三角形?
(3)作DQ∥AB交BC于点D,连接PD,当t为何值,△BDP∽△QPD?
典型例题
解析:(1)由题意可知BP=t,AQ=2t,则AP=6-t,由AP=2AQ可得到关于t的方程,可求得t的值;
(2)分∠APQ=90°和∠AQP=90°两种情况,再利用含30°角的直角三角形的性质可和AP=2AQ,或AQ=2AP,分别求t即可;
(3)由△BDP∽△PDQ可知∠BDP=∠PDQ,且∠BDQ+∠B=180°,可求得∠PDQ=60°,又∠PBD=∠PQD=60°=∠APQ,可证得△APQ为等边三角形,可得AP=AQ,得到关于t的方程,可求出t.
典型例题
解: :(1)由题意得:BP=t,AQ=2t,则AP=6-t,
由AP=2AQ得,6-t=4t,解得t= 即当t= 时,AP=2AQ;
(2)若△APQ为直角三角形,则∠APQ=90°或∠AQP=90°,
∴当t=3或t= 时,△APQ为直角三角形;
典型例题
(3)∵DQ∥AB,
∵CA=CB, ∴BD=AQ=2t,
又∵DQ∥AB, ∴∠APQ=∠PDQ,
当△BDP∽△PDQ时,∴∠B=∠PQD,
∴∠B=∠APQ=60°,∴△APQ为等边三角形,
∴AP=AQ,即6-t=2t,解得t=2.
所以当t=2时,△BDP∽△PDQ.
典型例题
3. 将平行四边形ABCD置于平面直角坐标系中,使得边A点与坐标原点重合,AB在x轴正半轴上,AB=8,AD=4,∠BAD=60°,动点P以1个单位每秒的速度从D点出发沿DC方向运动,设运动时间为t,过P点作PQ垂直x轴,垂足为Q(当Q点与B点重合时,P点停止运动),PQ与BD交于点H,点A、D关于PQ的对称点分别为点E、F,点G为射线EF与射线DB的交点.
(1)如图1,当点G在线段BD上时,求证:△HGE∽△ABD;
(2)t为何值时,△GHF是等腰三角形;
(3)P点运动过程中,设四边形EFQH与ABCD的重合部分面积为S,求S与t的函数关系式,并写出自变量取值范围.
典型例题
解析:(1)如图1中,取AB中点M,连接DM.首先证明∠ADB=90°,再证明∴∠HEG=∠ADB=90°,∠EHG=60°即可解决问题.
(2)分两种情形讨论①如图2中,当GH=GF时,设GF=HG=a,列出方程求出a.②如图3中,当FH=DG时,设FH=GF=a,列出方程求出a.
(3)分三种情形讨论①0≤t≤2,如图4中,重叠部分是四边形EFQH,②2<t≤4,如图5中,重叠部分是五边形EMBQH,③4<t≤6,如图6中,重叠部分是四边形MBQH,
典型例题
解:(1)如图1中,取AB中点M,连接DM.
∵AB=8,AM=BM,∴BM=AM=AD=4,∵∠DAM=60°,
∴△ADM是等边三角形,∴∠DMA=60°,DM=AM=BM=4,
∴∠MDB=∠MBD=30°,∴∠ADB=90°,∵AB∥CD,∴∠ABD=∠CDB=30°,∵点A、D关于PQ的对称点分别为点E、F,
∴∠HDE=∠HED=30°,∠HDA=∠HEG=90°,
∴∠EHG=∠HDE+∠HED=60°,
∴∠EHG=∠BAD,∠HEG=∠ADB=90°,
∴△△HGE∽△ABD.
典型例题
(2)①如图2中,当GH=GF时,设GF=HG=a,
典型例题
(2)①如图2中,当GH=GF时,设GF=HG=a,
典型例题
(2)②如图3中,当FH=DG时,设FH=GF=a,
典型例题
(3)①0≤t≤2,如图4中,重叠部分是四边形EFQH,
典型例题
(3)②2<t≤4,如图5中,重叠部分是五边形EMBQH,
典型例题
(3)③4<t≤6,如图6中,重叠部分是四边形MBQH,
巩固提升
如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片,点A在x轴上,点C在y轴上,且线段OA、OC(OA>OC)是方程x2-18x+80=0的两根,将边BC折叠,使点B落在边OA上的点D处.
(1)求线段OA、OC的长;
(2)求直线CE与x轴交点P的坐标及折痕CE的长;
(3)是否存在过点D的直线l,使直线CE与x轴、
y轴所围成的三角形和直线l、直线CE与y轴所围
成的三角形相似?如果存在,请直接写出其解
析式并画出相应的直线;如果不存在,请说明理由.
巩固提升
解析:(1)利用式子相乘法把方程左边分解为两一次因式积的形式,然后根据两数相乘积为0,两数中至少有一个为0,转化为两个一元一次方程,分别求出方程的解得到原方程的解,根据OA大于OC,即可得到OA及OC的长;
(2)由折叠可知三角形EBC与三角形EDC全等,根据全等三角形的对应边相等得到EB=ED,CB=CD,又矩形ABCD对边相等,从而得到CD的长,再由OC的长,利用勾股定理求出OD的长,进而求出AD的长,在直角三角形AED中,设EA=x,则DE=8-x,再由AD的长,利用勾股定理列出关于x的方程,求出方程的解得到AE的长,即为E的纵坐标,而OA的长即为E的横坐标,确定出E的坐标,同时得到BE的长,再由BC的长,在直角三角形BCE中,利用勾股定理求出折痕CE的长;
巩固提升
解析:(3)存在,应该有两条如图:
①直线BF,根据折叠的性质可知CE必垂直平分BD,那么∠DGP=∠CGF=90°,而∠CFG=∠DPG(都是∠OCP的余角),由此可得出两三角形相似,那么可根据B、D两点的坐标求出此直线的解析式.
②直线DN,由于∠FCD=∠NDO,那么可根据∠OCE即∠BEC的正切值,求出∠NDO的正切值,然后用OD的长求出ON的值,即可求出N点的坐标,然后根据N、D两点的坐标求出直线DN的解析式.
巩固提升
解:(1)方程x -18x+80=0,
因式分解得:(x-8)(x-10)=0,
即x-8=0或x-10=0, 解得:x1=8,x2=10,
∴OA=10,OC=8;
(2)由折叠可知:△EBC≌△EDC,∴EB=ED,
∴CB=CD,又矩形OABC,∴AB=OC=8,
∴CB=CD=OA=10,又OC=8,
巩固提升
∴AD=OA-OD=10-6=4,
又BE+EA=AB=8,且EB=ED,∴DE+EA=8,即DE=8-EA,
在Rt△AED中,设AE=x,则DE=8-x,又AD=4,
根据勾股定理得:(8-x) =x +16,整理得:16x=48,解得:x=3,
则E的坐标为(10,3),又C(0,8),设直线CE的解析式为y=kx+b,
解得:
令y=0求出x=16,即P坐标为(16,0);此时BE=BA-EA=8-3=5,又BC=OA=10,在Rt△BCE中,根据勾股定理得:
巩固提升
(3)存在.满足条件的直线l有2条:
y=-2x+12,y=2x-12.
如图2:准确画出两条直线.
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
动点综合问题(四)
通用版 中考复习
解读考点
知 识 点 名师点晴
动点问题中的特殊图形 等腰三角形与直角三角形 利用等腰三角形或直角三角形的特殊性质求解动点问题
相似问题 利用相似三角形的对应边成比例、对应角相等求解动点问题
动点问题中的计算问题 动点问题的最值与定值问题 理解最值或定值问题的求法
动点问题的面积问题 结合面积的计算方法来解决动点问题
动点问题的函数图象问题 一次函数或二次函数的图象 结合函数的图象解决动点问题
知识要点
专题四:函数中因动点产生的相似三角形问题
函数中因动点产生的相似三角形问题一般有三个解题途径:
① 求相似三角形的第三个顶点时,先要分析已知三角形的边和角的特点,进而得出已知三角形是否为特殊三角形。根据未知三角形中已知边与已知三角形的可能对应边分类讨论。
②或利用已知三角形中对应角,在未知三角形中利用勾股定理、三角函数、对称、旋转等知识来推导边的大小。
③若两个三角形的各边均未给出,则应先设所求点的坐标进而用函数解析式来表示各边的长度,之后利用相似来列方程求解。
典型例题
1.如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x-2交于B,C两点.
(1)求抛物线的解析式及点C的坐标;
(2)求△ABC的面积;
(3)若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由.
典型例题
解析:(1)可设顶点式,把原点坐标代入可求得抛物线解析式,联立直线与抛物线解析式,可求得C点坐标;
(2)设直线AC的解析式为y=kx+b,与x轴交于D,得到y=2x-1,求得
于是得到结论;
(3)设出N点坐标,可表示出M点坐标,从而可表示出MN、ON的长度,当△MON和△ABC相似时,利用三角形相似的性质可得
,可求得N点的坐标.
典型例题
解:(1)∵顶点坐标为(1,1),
∴设抛物线解析式为y=a(x-1) +1,
又抛物线过原点,
∴0=a(0-1) +1,解得a=-1,
∴抛物线解析式为y=-(x-1) +1,即y=-x +2x,
联立抛物线和直线解析式可得:
解得: ∴B(2,0),C(-1,-3);
典型例题
(2)设直线AC的解析式为y=kx+b,与x轴交于D,
把A(1,1),C(-1,-3)的坐标代入得
解得:
∴y=2x-1,当y=0,即2x-1=0,解得: x= 。
∴D( ,0)。
典型例题
(3)假设存在满足条件的点N,设N(x,0),则M(x,-x +2x),
∴ON=|x|,MN=|-x +2x|, 由(2)知,
∵MN⊥x轴于点N,∴∠ABC=∠MNO=90°,
∴当△ABC和△MNO相似时,
∵当x=0时M、O、N不能构成三角形,∴x≠0,
典型例题
即|x||-x+2|=3|x|,∴|-x+2|=3,
∴-x+2=±3,解得x=5或x=-1,
此时N点坐标为(-1,0)或(5,0),
综上可知存在满足条件的N点,其坐标或(-1,0)或(5,0).
典型例题
2.已知△ABC是边长为6cm的等边三角形,动点P、Q同时从B、A两点出发,分别沿BA、AC匀速运动,其中点P运动的速度是1cm/s,点Q运动的速度是2cm/s,当点Q到达点C时,P、Q两点都停止运动,设运动时间为t(s),解答下列问题:
(1)当t为何值时,AP=2AQ?
(2)当t为何值时,△APQ为直角三角形?
(3)作DQ∥AB交BC于点D,连接PD,当t为何值,△BDP∽△QPD?
典型例题
解析:(1)由题意可知BP=t,AQ=2t,则AP=6-t,由AP=2AQ可得到关于t的方程,可求得t的值;
(2)分∠APQ=90°和∠AQP=90°两种情况,再利用含30°角的直角三角形的性质可和AP=2AQ,或AQ=2AP,分别求t即可;
(3)由△BDP∽△PDQ可知∠BDP=∠PDQ,且∠BDQ+∠B=180°,可求得∠PDQ=60°,又∠PBD=∠PQD=60°=∠APQ,可证得△APQ为等边三角形,可得AP=AQ,得到关于t的方程,可求出t.
典型例题
解: :(1)由题意得:BP=t,AQ=2t,则AP=6-t,
由AP=2AQ得,6-t=4t,解得t= 即当t= 时,AP=2AQ;
(2)若△APQ为直角三角形,则∠APQ=90°或∠AQP=90°,
∴当t=3或t= 时,△APQ为直角三角形;
典型例题
(3)∵DQ∥AB,
∵CA=CB, ∴BD=AQ=2t,
又∵DQ∥AB, ∴∠APQ=∠PDQ,
当△BDP∽△PDQ时,∴∠B=∠PQD,
∴∠B=∠APQ=60°,∴△APQ为等边三角形,
∴AP=AQ,即6-t=2t,解得t=2.
所以当t=2时,△BDP∽△PDQ.
典型例题
3. 将平行四边形ABCD置于平面直角坐标系中,使得边A点与坐标原点重合,AB在x轴正半轴上,AB=8,AD=4,∠BAD=60°,动点P以1个单位每秒的速度从D点出发沿DC方向运动,设运动时间为t,过P点作PQ垂直x轴,垂足为Q(当Q点与B点重合时,P点停止运动),PQ与BD交于点H,点A、D关于PQ的对称点分别为点E、F,点G为射线EF与射线DB的交点.
(1)如图1,当点G在线段BD上时,求证:△HGE∽△ABD;
(2)t为何值时,△GHF是等腰三角形;
(3)P点运动过程中,设四边形EFQH与ABCD的重合部分面积为S,求S与t的函数关系式,并写出自变量取值范围.
典型例题
解析:(1)如图1中,取AB中点M,连接DM.首先证明∠ADB=90°,再证明∴∠HEG=∠ADB=90°,∠EHG=60°即可解决问题.
(2)分两种情形讨论①如图2中,当GH=GF时,设GF=HG=a,列出方程求出a.②如图3中,当FH=DG时,设FH=GF=a,列出方程求出a.
(3)分三种情形讨论①0≤t≤2,如图4中,重叠部分是四边形EFQH,②2<t≤4,如图5中,重叠部分是五边形EMBQH,③4<t≤6,如图6中,重叠部分是四边形MBQH,
典型例题
解:(1)如图1中,取AB中点M,连接DM.
∵AB=8,AM=BM,∴BM=AM=AD=4,∵∠DAM=60°,
∴△ADM是等边三角形,∴∠DMA=60°,DM=AM=BM=4,
∴∠MDB=∠MBD=30°,∴∠ADB=90°,∵AB∥CD,∴∠ABD=∠CDB=30°,∵点A、D关于PQ的对称点分别为点E、F,
∴∠HDE=∠HED=30°,∠HDA=∠HEG=90°,
∴∠EHG=∠HDE+∠HED=60°,
∴∠EHG=∠BAD,∠HEG=∠ADB=90°,
∴△△HGE∽△ABD.
典型例题
(2)①如图2中,当GH=GF时,设GF=HG=a,
典型例题
(2)①如图2中,当GH=GF时,设GF=HG=a,
典型例题
(2)②如图3中,当FH=DG时,设FH=GF=a,
典型例题
(3)①0≤t≤2,如图4中,重叠部分是四边形EFQH,
典型例题
(3)②2<t≤4,如图5中,重叠部分是五边形EMBQH,
典型例题
(3)③4<t≤6,如图6中,重叠部分是四边形MBQH,
巩固提升
如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片,点A在x轴上,点C在y轴上,且线段OA、OC(OA>OC)是方程x2-18x+80=0的两根,将边BC折叠,使点B落在边OA上的点D处.
(1)求线段OA、OC的长;
(2)求直线CE与x轴交点P的坐标及折痕CE的长;
(3)是否存在过点D的直线l,使直线CE与x轴、
y轴所围成的三角形和直线l、直线CE与y轴所围
成的三角形相似?如果存在,请直接写出其解
析式并画出相应的直线;如果不存在,请说明理由.
巩固提升
解析:(1)利用式子相乘法把方程左边分解为两一次因式积的形式,然后根据两数相乘积为0,两数中至少有一个为0,转化为两个一元一次方程,分别求出方程的解得到原方程的解,根据OA大于OC,即可得到OA及OC的长;
(2)由折叠可知三角形EBC与三角形EDC全等,根据全等三角形的对应边相等得到EB=ED,CB=CD,又矩形ABCD对边相等,从而得到CD的长,再由OC的长,利用勾股定理求出OD的长,进而求出AD的长,在直角三角形AED中,设EA=x,则DE=8-x,再由AD的长,利用勾股定理列出关于x的方程,求出方程的解得到AE的长,即为E的纵坐标,而OA的长即为E的横坐标,确定出E的坐标,同时得到BE的长,再由BC的长,在直角三角形BCE中,利用勾股定理求出折痕CE的长;
巩固提升
解析:(3)存在,应该有两条如图:
①直线BF,根据折叠的性质可知CE必垂直平分BD,那么∠DGP=∠CGF=90°,而∠CFG=∠DPG(都是∠OCP的余角),由此可得出两三角形相似,那么可根据B、D两点的坐标求出此直线的解析式.
②直线DN,由于∠FCD=∠NDO,那么可根据∠OCE即∠BEC的正切值,求出∠NDO的正切值,然后用OD的长求出ON的值,即可求出N点的坐标,然后根据N、D两点的坐标求出直线DN的解析式.
巩固提升
解:(1)方程x -18x+80=0,
因式分解得:(x-8)(x-10)=0,
即x-8=0或x-10=0, 解得:x1=8,x2=10,
∴OA=10,OC=8;
(2)由折叠可知:△EBC≌△EDC,∴EB=ED,
∴CB=CD,又矩形OABC,∴AB=OC=8,
∴CB=CD=OA=10,又OC=8,
巩固提升
∴AD=OA-OD=10-6=4,
又BE+EA=AB=8,且EB=ED,∴DE+EA=8,即DE=8-EA,
在Rt△AED中,设AE=x,则DE=8-x,又AD=4,
根据勾股定理得:(8-x) =x +16,整理得:16x=48,解得:x=3,
则E的坐标为(10,3),又C(0,8),设直线CE的解析式为y=kx+b,
解得:
令y=0求出x=16,即P坐标为(16,0);此时BE=BA-EA=8-3=5,又BC=OA=10,在Rt△BCE中,根据勾股定理得:
巩固提升
(3)存在.满足条件的直线l有2条:
y=-2x+12,y=2x-12.
如图2:准确画出两条直线.
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
同课章节目录
