4.1.2 点、线、面、体培优辅导训练(附答案)
文档属性
| 名称 | 4.1.2 点、线、面、体培优辅导训练(附答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-25 00:00:00 | ||
图片预览

文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
4.1.2点、线、面、体
知识梳理
几何图形都是由 、线、 、体组成的。 是构成图形的基本元素,而 也是最简单的几何图形。
(1)体: 简称为体。
(2)面:包围着体的是面,面分为 和 。
(3)线: 相交的地方形成线,线分为 和 。
(4)点: 相交的地方是点。
(5)点动成 、 动成面、面动成 。
重点突破
知识点 点、线、面、体之间的关系
1.航天飞机拖着“长长的火焰”,我们用数学知识可解释为点动成线.用数学知识解释下列现象:
(1)一只小蚂蚁爬行留下的路线可解释为 .
(2)电动车车辐条运动形成的图形可解释为 .
(3)薄薄的硬币在桌面上转动时,看上去像球,这说明了 .
【解析】本题主要考查点、线、面、体之间的关系. 从运动的观点可知,(1)蚂蚁可以看做一个点,它爬行的路线看上去形成一条线,这种现象说明点动成线;(2)车辐条可以看做是一条线段绕一点 旋转形成一个圆形的面,这种现象说明线动成面;(3)薄薄的硬币在桌面上转动时,看上去像球,这种现象说明面转动成体.
【答案】(1)点动成线;(2)线动成面;(3)面动成体.
基础过关
1.下面几何体中,全是由曲面围成的是( )
A.圆锥 B.正方体 C.圆柱 D.球
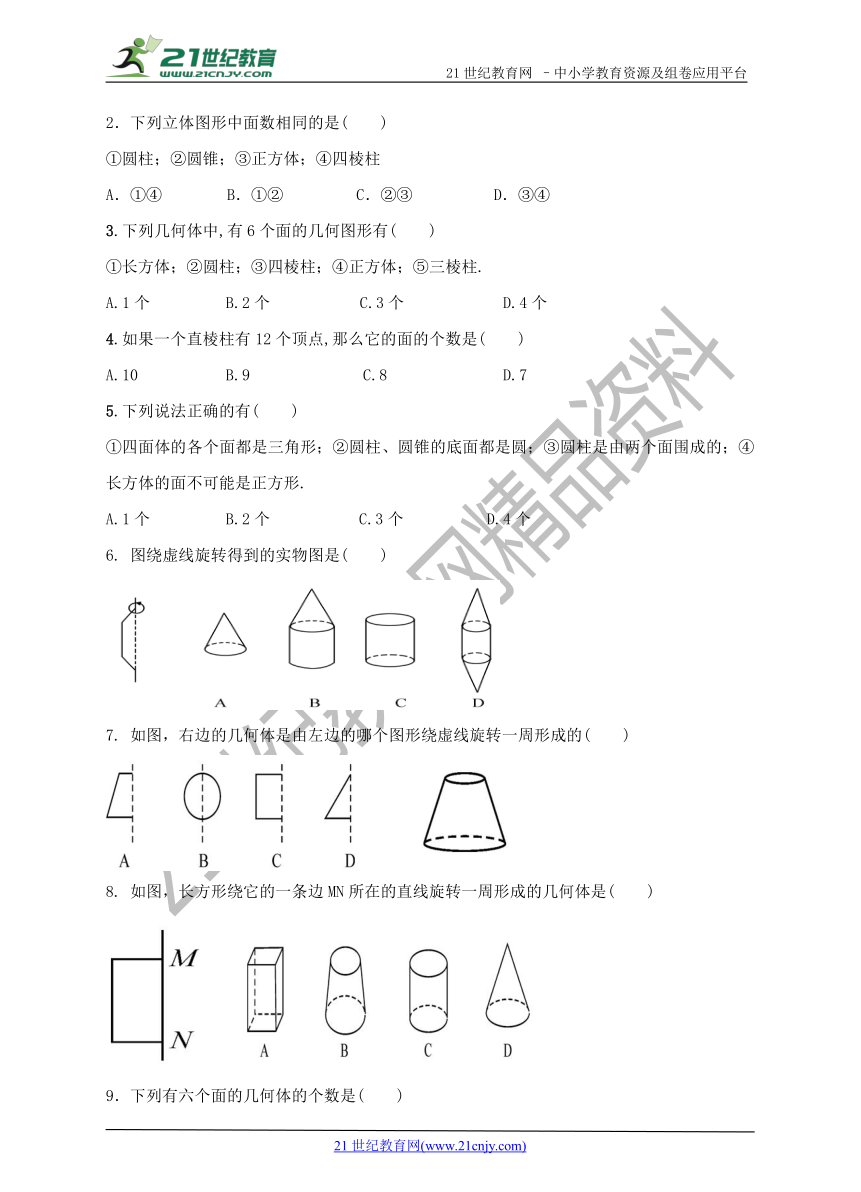
2.下列立体图形中面数相同的是( )
①圆柱;②圆锥;③正方体;④四棱柱
A.①④ B.①② C.②③ D.③④
3.下列几何体中,有6个面的几何图形有( )
①长方体;②圆柱;③四棱柱;④正方体;⑤三棱柱.
A.1个 B.2个 C.3个 D.4个
4.如果一个直棱柱有12个顶点,那么它的面的个数是( )
A.10 B.9 C.8 D.7
5.下列说法正确的有( )
①四面体的各个面都是三角形;②圆柱、圆锥的底面都是圆;③圆柱是由两个面围成的;④长方体的面不可能是正方形.
A.1个 B.2个 C.3个 D.4个
6. 图绕虚线旋转得到的实物图是( )
7. 如图,右边的几何体是由左边的哪个图形绕虚线旋转一周形成的( )
8. 如图,长方形绕它的一条边MN所在的直线旋转一周形成的几何体是( )
9.下列有六个面的几何体的个数是( )
①长方体;②圆柱;③四棱柱;④正方体;⑤三棱柱
A.1个 B.2个 C.3个 D.4个
10.天空中的流星划过后留下的光线,给我们以什么样的形象( )
A.点 B.线 C.面 D.体
11.在以下四个几何体中,其侧面展开图不是平面图形的是( )
A.圆柱 B.棱柱 C.球 D.圆锥
12.将三角形绕直线L旋转一周,可以得到如下图所示立体图形的是( )
A B C D
13.如图,正方形ABCD的边长为3 cm,以直线AB为轴,将正方形旋转一周,所得几何体从正面看的图形的面积是 cm2.
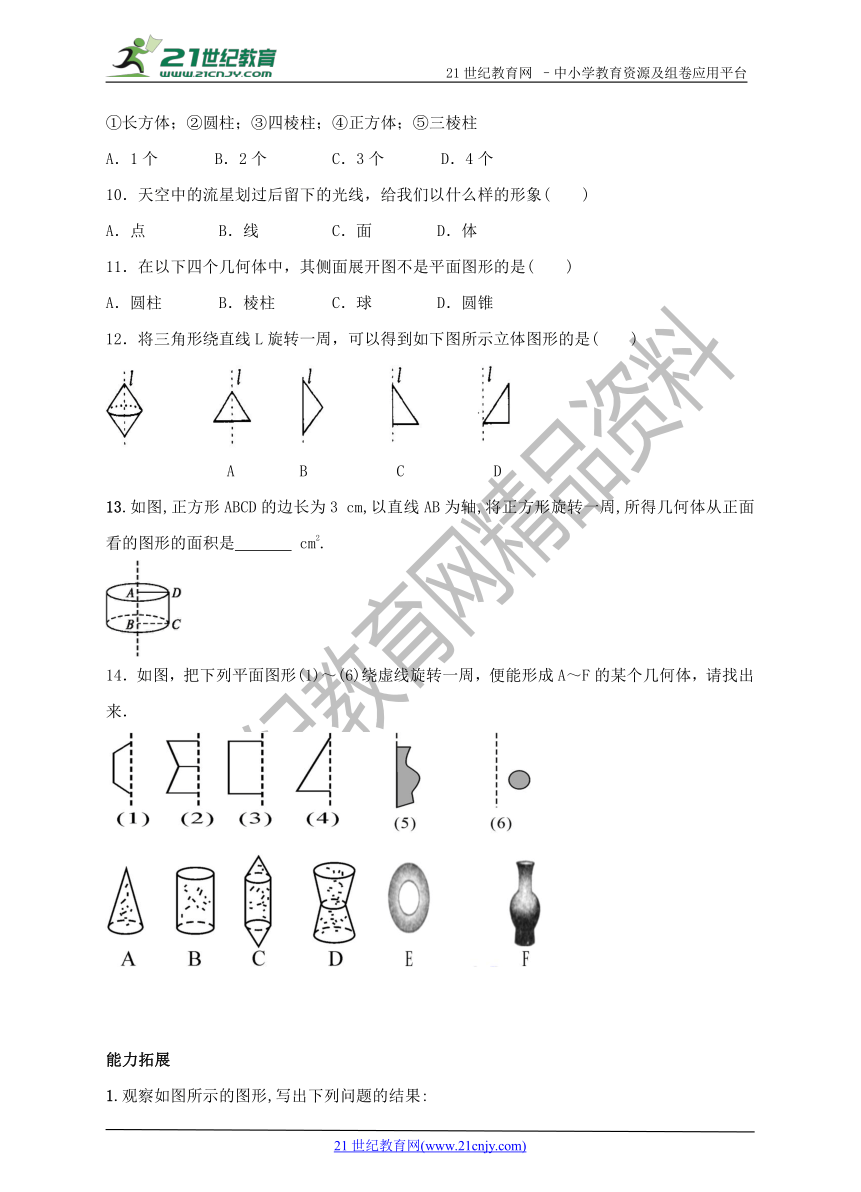
14.如图,把下列平面图形(1)~(6)绕虚线旋转一周,便能形成A~F的某个几何体,请找出来.21cnjy.com
能力拓展
1.观察如图所示的图形,写出下列问题的结果:
(1)这个图形的名称是 ;
(2)这个几何体有 个面,有 个底面,有 个侧面,底面是 形,侧面是 形.
(3)侧面的个数与底面多边形的边数有什么关系
2.用数学的眼光去观察问题,你会发现很多图形都能看成是动静结合,舒展自如的.下面所给的三排图形都存在着某种联系,用线将它们连起来.
3.观察下列多面体,并把下表补充完整.
观察上表中的结果,你能发现a,b,c之间有什么关系吗 请写出关系式.
4.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题:
(1)根据上面多面体模型,完成表格中的空格:
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是 .
(2)一个多面体的面数比顶点数大8,且有30条棱,求这个多面体的面数.
(3)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱,设该多面体外表三角形的个数为x个,八边形的个数为y个,求x+y的值.
参考答案
4.1.2点、线、面、体
知识梳理
点,面,点,点;几何体;平面,曲面;面与面,曲线,直线;线与线;线,线,体。
基础过关
1.D
2.D
3. C
4. C
5. B
6. D
7. A
8. C
9.C
10.B
11.C
12.B
13.18
14.解:(1)~(6)分别对应C,D,B,A,F,E
能力拓展
1.解:(1)六棱柱
(2)8 2 6 六边 长方
(3)侧面的个数与底面多边形的边数相等.
2.解:从第一行的平面图形绕某一边旋转或沿某一方向平移可得到第二行的立体图形,从第二行的立体图形的上面看可得到第三行的平面图形.
(1)→(三)→(D);
(2)→(二)→(C);
(3)→(四)→(B);
(4)→(一)→(A).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
4.1.2点、线、面、体
知识梳理
几何图形都是由 、线、 、体组成的。 是构成图形的基本元素,而 也是最简单的几何图形。
(1)体: 简称为体。
(2)面:包围着体的是面,面分为 和 。
(3)线: 相交的地方形成线,线分为 和 。
(4)点: 相交的地方是点。
(5)点动成 、 动成面、面动成 。
重点突破
知识点 点、线、面、体之间的关系
1.航天飞机拖着“长长的火焰”,我们用数学知识可解释为点动成线.用数学知识解释下列现象:
(1)一只小蚂蚁爬行留下的路线可解释为 .
(2)电动车车辐条运动形成的图形可解释为 .
(3)薄薄的硬币在桌面上转动时,看上去像球,这说明了 .
【解析】本题主要考查点、线、面、体之间的关系. 从运动的观点可知,(1)蚂蚁可以看做一个点,它爬行的路线看上去形成一条线,这种现象说明点动成线;(2)车辐条可以看做是一条线段绕一点 旋转形成一个圆形的面,这种现象说明线动成面;(3)薄薄的硬币在桌面上转动时,看上去像球,这种现象说明面转动成体.
【答案】(1)点动成线;(2)线动成面;(3)面动成体.
基础过关
1.下面几何体中,全是由曲面围成的是( )
A.圆锥 B.正方体 C.圆柱 D.球
2.下列立体图形中面数相同的是( )
①圆柱;②圆锥;③正方体;④四棱柱
A.①④ B.①② C.②③ D.③④
3.下列几何体中,有6个面的几何图形有( )
①长方体;②圆柱;③四棱柱;④正方体;⑤三棱柱.
A.1个 B.2个 C.3个 D.4个
4.如果一个直棱柱有12个顶点,那么它的面的个数是( )
A.10 B.9 C.8 D.7
5.下列说法正确的有( )
①四面体的各个面都是三角形;②圆柱、圆锥的底面都是圆;③圆柱是由两个面围成的;④长方体的面不可能是正方形.
A.1个 B.2个 C.3个 D.4个
6. 图绕虚线旋转得到的实物图是( )
7. 如图,右边的几何体是由左边的哪个图形绕虚线旋转一周形成的( )
8. 如图,长方形绕它的一条边MN所在的直线旋转一周形成的几何体是( )
9.下列有六个面的几何体的个数是( )
①长方体;②圆柱;③四棱柱;④正方体;⑤三棱柱
A.1个 B.2个 C.3个 D.4个
10.天空中的流星划过后留下的光线,给我们以什么样的形象( )
A.点 B.线 C.面 D.体
11.在以下四个几何体中,其侧面展开图不是平面图形的是( )
A.圆柱 B.棱柱 C.球 D.圆锥
12.将三角形绕直线L旋转一周,可以得到如下图所示立体图形的是( )
A B C D
13.如图,正方形ABCD的边长为3 cm,以直线AB为轴,将正方形旋转一周,所得几何体从正面看的图形的面积是 cm2.
14.如图,把下列平面图形(1)~(6)绕虚线旋转一周,便能形成A~F的某个几何体,请找出来.21cnjy.com
能力拓展
1.观察如图所示的图形,写出下列问题的结果:
(1)这个图形的名称是 ;
(2)这个几何体有 个面,有 个底面,有 个侧面,底面是 形,侧面是 形.
(3)侧面的个数与底面多边形的边数有什么关系
2.用数学的眼光去观察问题,你会发现很多图形都能看成是动静结合,舒展自如的.下面所给的三排图形都存在着某种联系,用线将它们连起来.
3.观察下列多面体,并把下表补充完整.
观察上表中的结果,你能发现a,b,c之间有什么关系吗 请写出关系式.
4.十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题:
(1)根据上面多面体模型,完成表格中的空格:
你发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是 .
(2)一个多面体的面数比顶点数大8,且有30条棱,求这个多面体的面数.
(3)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱,设该多面体外表三角形的个数为x个,八边形的个数为y个,求x+y的值.
参考答案
4.1.2点、线、面、体
知识梳理
点,面,点,点;几何体;平面,曲面;面与面,曲线,直线;线与线;线,线,体。
基础过关
1.D
2.D
3. C
4. C
5. B
6. D
7. A
8. C
9.C
10.B
11.C
12.B
13.18
14.解:(1)~(6)分别对应C,D,B,A,F,E
能力拓展
1.解:(1)六棱柱
(2)8 2 6 六边 长方
(3)侧面的个数与底面多边形的边数相等.
2.解:从第一行的平面图形绕某一边旋转或沿某一方向平移可得到第二行的立体图形,从第二行的立体图形的上面看可得到第三行的平面图形.
(1)→(三)→(D);
(2)→(二)→(C);
(3)→(四)→(B);
(4)→(一)→(A).
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
