动生电动势13种题型破解
图片预览




文档简介
动生电动势13种题型破解
在电磁感应现象中,部分导体或可导回路往往会相对于磁场做切割磁感线的运动。我们可以把此导体或可导回路称作“切割导体”,简称“切导”。
所谓动生电动势,指与磁场做相对、切割磁感线的运动“切导”中产生的感应电动势。这里应该强调,产生动生电动势必须具备两个必要条件,即一则“切导”与磁场有相对运动现象发生;二则该“切导”必须切割磁感线。实际上,“切导”的定义本身即包含着这两方面的意义。
一、破解依据
欲解决此类问题,大致归纳为以下几条“依据”:
㈠产生动生电动势的条件(略).
㈡大小计算:⑴其中,n为回路匝数,为回路面积的变化率。
⑵,其中E、B、v等两两垂直,l可视为“有效(切割)长度”——部分或整体回路在垂直于磁场方向的“投影长度”。⑶,其中为动生电动势的最大值。⑷,其中,l做定轴转动。
㈢方向判定:“手心对N极、拇指表运动、四指示动(生)电(流)”——右手定则。与“手心对N极、四指表通电、拇指示受力”——左手定则显著不同。
㈣另一重要推论:其中q、R分别为流过单匝回路的电荷量及其电阻。
㈤“切导回路”与“磁场”的相互作用,对应“增反减同”规律则有“进则推拒,出却扯拉”,简称作“进推出拉”的规律。
㈥若涉及外电路变换、变化以及电流、电压、功率、效益等,则需综合应用“恒定电流”的有关概念和规律。
㈦若涉及冲动联系、动量定理、动量守恒与功能联系(如动能定理)、能量转化和守恒等等,则宜采用相应手段处理。
二、解题示例
所谓“切导回路”,即由正在做切割运动的导体组成的回路,如由金属组成的各种形式的线圈、线框等。在匀强磁场或有界匀强磁场中做平动的切导回路中,必定产生动生电动势。动生电动势的大小常常由于回路的“有效长度”或“面积变化”的不同而不同。
一、“切导回路”垂直于磁场方向的平动问题
若匀强磁场与“切导回路”所在平面垂直,其沿垂直于磁场方向自进入、于内到离开过程中,自然随之带来动生电动势、动生电流的有无确认、大小计算、方向判断以及功能分析、能量转换与守恒应用等等一系列问题。请读者看下面的典型例题的解决过程。
[例题1](’04江苏)如图—1所示,一个有界匀强磁场区域,磁场方向垂直纸面向外.一个矩形闭合导线框abcd,沿纸面由位置1(左)匀速运动到位置2(右).则
(A)导线框进入磁场时,感应电流方向为a→b→c→d→a
(B)导线框离开磁场时,感应电流方向为a→d→c→b→a
(C)导线框离开磁场时,受到的安培力方向水平向右
(D)导线框进入磁场时.受到的安培力方向水平向左
[解析]首先,当导线框“进入”磁场时,由“依据”㈠、㈢(右手定则)可知,动生(或感应)电流沿顺时针方向;“离开”时,则沿逆时针方向。故知选项A、B均错。
然后,由依据㈤(即“进推出拉”规律)(或左手定则),可判断“进入”时,安培力向左;“离开”时亦向左。故知选项C错而D对。
因此,本题答案为:D。
[点拨]应该强调,左手定则判“受力”,右手定则断“感电”;无论磁场、感应电流方向如何,因而“切导”所受安培力总与为运动“阻力”。
[例题2](’05全国Ⅰ)图中两条平行虚线之间存在匀强磁场,虚线间的距离为l,磁场方向垂直纸面向里。abcd是位于纸面内的梯形线圈,ad与bc间的距离也为l。t=0时刻,bc边与磁场区域边界重合(如图)。现令线圈以恒定的速度v沿垂直于磁场区域边界的方向穿过磁场区域。取沿a→b→c→d→a的感应电流为正,则在线圈穿越磁场区域的过程中,感应电流I随时间t变化的图线可能是()
[解析]首先,设梯形线圈的左底边长为l0,分析水平向右匀速“进入”、“离开“磁场时,易知其“有效长度”均为
其中。再设线圈电阻为R,由依据㈡⑵、欧姆定律可得电流大小
显然,I为t的一次函数,随时间增大而均匀增大。
然后,应用依据㈢,可知线圈“进入”则电流为负;“离开”则为正。
综上所述,可知本题答案为:B。
[例题3](’07全国Ⅰ)如图—4所示,LOO/L/为一折线,它所形成的两个角∠LOO/和∠OO/L/均为45°。折线的右边有一匀强磁场。其方向垂直于纸面向里。一边长为l的正方形导线框沿垂直于OO/的方向以速度v作匀速直线运动,在t=0的刻恰好位于图中所示位置。以逆时针方向为导线框中电流的正方向,在上面四幅图中能够正确表示电流-时(I-t)关系的是(时间以I/v为单位)
[解析]首先,正方形导线框在三段连续相等的时间内,其“有效长度”经历先增大至最大而迅即为零、后增至最大、再后由最大减小为零等非连续“均匀变化”过程。又由于“磁强”B、速度v等均未改变。由依据㈠、㈡,可知该切导回路的电动势的大小亦随之做类似变化。
然后,再应用依据㈢(右手定则)可知,电流方向经历先正、后负、再后亦负的变化过程。
因此,本题答案为:D。
[点拨]由例2、3解析可见,对匀强磁场中切导回路而言,欲求感应电动势的大小,先须求出回路的“有效长度”。
[例题4](’00全国)空间存在以ab、cd为边界的匀强磁场区域,磁感强度大小为B,方向垂直纸面向外,区域宽为l1。现有一矩框处在图中纸面内,它的短边与ab重合,长度为l2,长边的长度为2l1,如图—5所示,某时刻线框以初速v沿与ab垂直的方向进入磁场区域,同时某人对线框施以作用力,使它的速度大小和方向保持不变。设该线框的电阻为R。从线框开始进入磁场到完全离开磁场的过程中,人对线框作用力所做的功等于___________________。
[解析]首先,显见切导回路的有效切割长度为l2,切割运动的实际位移为2l1。从而,由“依据”㈡⑵、欧姆定律和安培力公式得
已知线框作匀速直线运动,因而其水平方向受力平衡,亦即人对线框作用力与安培力的“等大反向”,人对线框作用力所做的功大小等于安培力所做的功。设人所做的功为W。从而,可得
[点拨]前已说明,安培力总为“切导”运动的阻力;进而指出,安培力做功必定消耗系统的机械能(或曰电能),而此能量的减小表现为等量的热损耗。
[例题5](’06上海)如图—6所示,将边长为a、质量为m、电阻为R的正方形导线框竖直向上抛出,穿过宽度为b、磁感应强度为B的匀强磁场,磁场的方向垂直纸面向里.线框向上离开磁场时的速度刚好是进人磁场时速度的一半,线框离开磁场后继续上升一段高度,然后落下并匀速进人磁场。整个运动过程中始终存在着大小恒定的空气阻力f且线框不发生转动。求:
⑴线框在下落阶段匀速进人磁场时的速度v2;
⑵线框在上升阶段刚离开磁场时的速度v1;
⑶线框在上升阶段通过磁场过程中产生的焦耳热Q。
[解析]⑴首先,线框之所以在下落阶段匀速进入,一定是在竖直方向受力平衡。从而,则有
由此解得
⑵其次,在线框离开磁场的上升阶段、下落阶段,由动能定理可得
联立①②③式,即可求出
⑶然后,已知线框穿越磁场进入、离开时的速度分别为v1、v2。从而,由功能关系可得
联立④⑤⑥式,我们即可求出线框在上升阶段通过磁场过程中产生的焦耳热
[点拨]应该说明,在讨论“切导”在磁场中的运动时,对系统的受力、运动、功能等三种分析是完全必要的。由解析可见,动能定理、功能关系在这里起了至关重要的作用。
[例题6](’07重庆)t=0时,磁场在xOy平面内的分布如题—7图所示。其磁感应强度的大小均为B0,方向垂直于xOy平面,相邻磁场区域的磁场方向相反。每个同向磁场区域的宽度均为l0。整个磁场以速度v沿x轴正方向匀速运动。
⑴若在磁场所在区间,xOy平面内放置一由a匝线圈串联而成的矩形导线框abcd,线框的bc边平行于x轴。bc=l0、ab=L,总电阻为R,线框始终保持静止。求
①线框中产生的总电动势大小和导线中的电流大小;
②线框所受安培力的大小和方向。
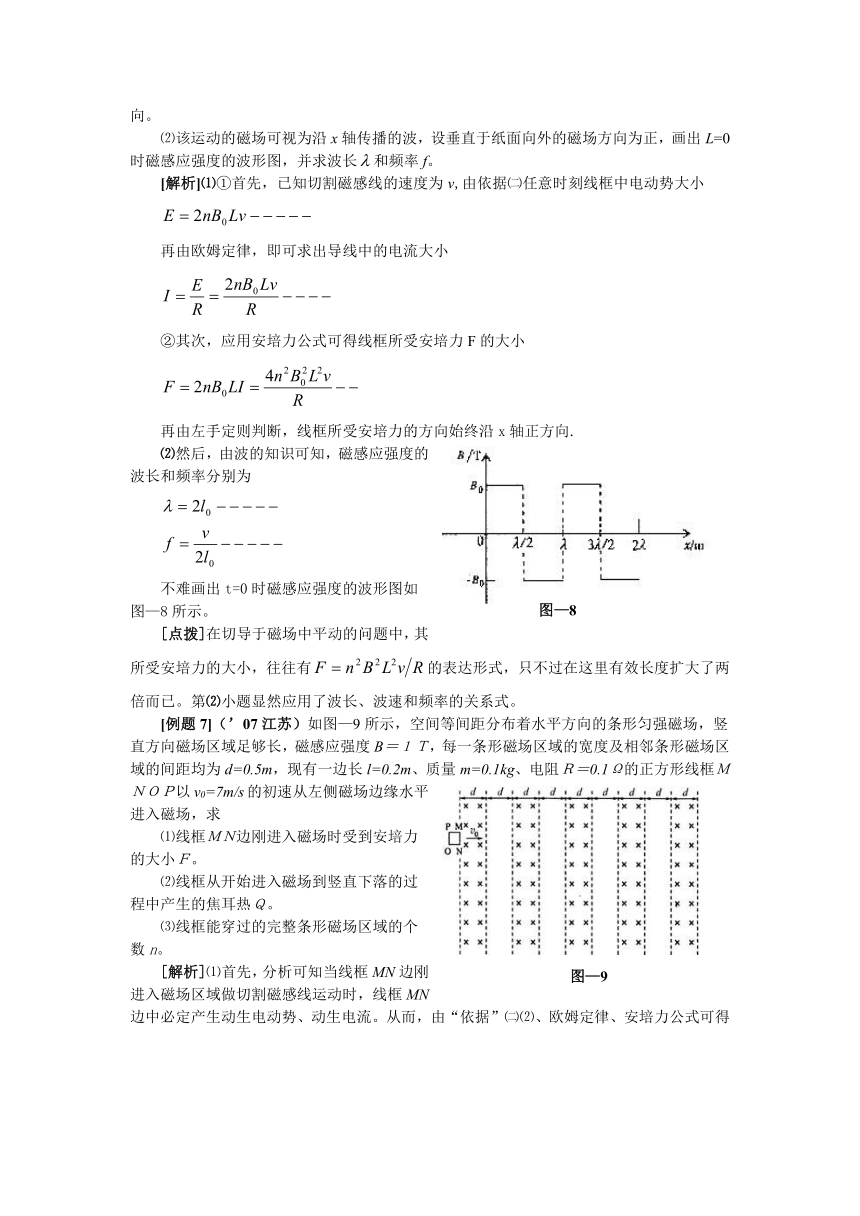
⑵该运动的磁场可视为沿x轴传播的波,设垂直于纸面向外的磁场方向为正,画出L=0时磁感应强度的波形图,并求波长和频率f。
[解析]⑴①首先,已知切割磁感线的速度为v,由依据㈡任意时刻线框中电动势大小
再由欧姆定律,即可求出导线中的电流大小
②其次,应用安培力公式可得线框所受安培力F的大小
再由左手定则判断,线框所受安培力的方向始终沿x轴正方向.
⑵然后,由波的知识可知,磁感应强度的波长和频率分别为
不难画出t=0时磁感应强度的波形图如图—8所示。
[点拨]在切导于磁场中平动的问题中,其所受安培力的大小,往往有的表达形式,只不过在这里有效长度扩大了两倍而已。第⑵小题显然应用了波长、波速和频率的关系式。
[例题7](’07江苏)如图—9所示,空间等间距分布着水平方向的条形匀强磁场,竖直方向磁场区域足够长,磁感应强度B=1T,每一条形磁场区域的宽度及相邻条形磁场区域的间距均为d=0.5m,现有一边长l=0.2m、质量m=0.1kg、电阻R=0.1Ω的正方形线框MNOP以v0=7m/s的初速从左侧磁场边缘水平进入磁场,求
⑴线框MN边刚进入磁场时受到安培力的大小F。
⑵线框从开始进入磁场到竖直下落的过程中产生的焦耳热Q。
⑶线框能穿过的完整条形磁场区域的个数n。
[解析]⑴首先,分析可知当线框MN边刚进入磁场区域做切割磁感线运动时,线框MN边中必定产生动生电动势、动生电流。从而,由“依据”㈡⑵、欧姆定律、安培力公式可得
联立①②③式,代如已知数据,即可求出此时受到安培力的大小
⑵其次,在线框从开始进入磁场到竖直下落的过程中,重力做正功而电能转变为电热。设线框竖直下落时,线框下落了h,速度为vt,从而由自由落体运动规律、功能关系可得
联立④⑤式,可求出过程中产生的焦耳热为
⑶然后,由于只有在线框进入和穿出条形磁场区域时,才产生感应电动势。从而,由“依据”㈡⑵、欧姆定律和安培力公式,可得线框部分进入磁场区域x时所受的安培力为
由此可见,安培力是速度的函数。欲求穿过的完整条形磁场区域的个数n,尝试在t→t+△t时间内应用动量定理。由此,可得
以后,在时间t或磁场区域x内,对②式求和可得
由③式即可解得
显然
最后代入已知数据,我们可以求出
即线框能穿过的完整条形磁场区域的个数为4个。
[点拨]此例应为一道力、热、电综合性极强、难度亦较大的高考试题,属于此类问题中的佼佼者。动量定理的必要、巧妙的引入和应用,令人开扩眼界和痛感欣慰。若换一方式,从讨论线框穿过第1个条形磁场过程入手。先取其平均感应电动势为,类似地,可得平均力的冲量。显然,平均力冲量是恒量,与穿越时间无关。依次类推,穿越n个条形磁场则皆然。从而,由动量定理得。进而可求出相同的结果。
二、“切导回路”垂直于磁场的另一种平动问题。
若匀强磁场与“切导回路”平面“平行”,当其沿垂直于磁场方向平动时,类似地,亦随之带来一系列动生电动势、动生电流等等相应问题。
下面,我们先来讨论由笔者编制的一道“08高考预测题”。
[例题8](’08自编预测)如图—10所示,一环形磁铁的外管、内柱分别为N极、S极,之间的区域可视为辐向分布的匀强磁场,磁感应强度为B。现垂直于磁场方向放入一个匝数为n、半径为r、导线单位长度的电阻为的圆形线圈。试求:⑴当线圈以速度v垂直于纸面向内运动时,动生电动势的大小和方向?⑵设通过线圈的恒定电流为I,线圈的机械功率多大?⑶若线圈垂直于纸面振动,其瞬时速度表达式为,动生电流的功率。
[解析]⑴首先,显见回路的“有效切割长度”等于回路的周长,即。
由依据㈡、㈢(即动生电动势公式和右手定则)可得
显见,线圈的动生电动势(或动生电流)方向为逆时针的。
⑵其次,设线圈的机械功率为P,则由功率关系、电阻计算式得
联立①②③式,即可求出
⑶然后,欲求电流的功率,须求电动势、电流的有效值。从而,由依据㈡可得电动势的最大值
进而,设I/、E/为电流、电动势的有效值,p/为动生电流的功率。由交变电流知识可得
最后,联立③④⑤式,即可求出以下结果
[点拨]假如在该磁场中,放入垂直于纸面的长为L金属棒,当其绕O点匀或变速转动时,由依据㈡可得,再结合左手定则,我们仍不难求出其动生电动势的大小和方向。
[例题9](’07北京)用密度为d.电阻率为、横截面积为A的薄金属条制成边长为L的闭合正方形框。如图—11所示,金属方框水平放在磁极的狭缝间,方框平面与磁场方向平行。设匀强磁场仅存在于相对磁极之间,其他地方的磁场忽略不计。可认为方框的边和边都处在磁极之间,极间磁感应强度大小为B。方框从静止开始释放,其平面在下落过程中保持水平(不计空气阻力)。
⑴求方框下落的最大速度vm(设磁场区域在竖直方向足够长);
⑵当方框下落的加速度为时,求方框的发热功率P;
⑶已知方框下落时间为t时,下落高度为h,其速度为vt(vt[解析]⑴首先,分析可知“切导”方框受向下的重力和向上的安培力(“依据”㈢)作用,沿竖直向下做变加速运动。从而,设框的下落速度为v,考虑到已知条件,应用安培力公式、依据㈡(动生电动势公式)、电磁感应定律、欧姆定律可得
再由质量计算式、电阻定律等,可知
其次,由①②③式、牛二定律可得
当加速度等于零时,即当时,方框达到最大速度vm。亦即
由此可得,方框下落的最大速度
⑵然后,当方框下落加速度为时,再由牛二定律、电功率公式得
联立②③⑥⑦式,即可求出方框的发热功率
⑶最后,根据能量守恒定律,可得
再联立②③⑧式,即可求出恒定电流的表达式
[点拨]应该指出,欲求方框的最大速度,必须先应用牛二定律写出加速度的瞬时表达式,再由物体的速度变化的规律可知,“加速度为零”是速度达到最大的必要条件。与力学问题不同的是,求合力必须考虑“通导”所受的安培力。而能量守恒则为重力势能的减少等于动能、内能的增加(转为热量放出)。
三、“切导回路”在匀强磁场中的转动(或振动)问题
以下几例为由于“切导回路”在有界磁场中转动,从而产生动生电动势的问题。
[例题10](经典试题)半径为r、质量为m、电阻为R的金属圆环,用一根长为L的绝缘细绳悬挂于O点,宽度为L/4的垂直向里的匀强磁场的上边界到O点的距离为L/2,如图—12所示。现使圆环由与悬点等高的A点由静止释放,若运动过程中圆环所在平面始终垂直于磁场,则圆环产生的焦耳热是()
A.mgLB.mg(L/2+r)C.mg(3L/4+r)D.mg(L+2r)
[解析]首先,分析环的运动过程,可知每当金属圆环进入、离开磁场时,由依据㈢(右手定则)、左手定则可知其均受阻力——安培力的作用。因此由功能关系可知,环的机械能将不断减少,减少的机械能则转化为焦耳热。
然后,显见当环运动到磁场下边界之外,亦即如图—13的位置时,环不再切割磁感应线而安培力消失,故知此后机械能即不再减少,亦不会再有焦耳热产生。从而,由功能关系可得
因此,本题答案为:C。
[点拨]我们又一次看到,当“切导回路”进、出磁场时,由于受“进推出拉”的安培阻力故使系统的机械能减少,其实则转化为焦耳热。
[例题11](’07枣庄调研)长为a、宽为b的矩形线框有n匝,每匝线圈电阻为R。如图—14所示,对称轴MN的左侧有磁感应强度为B的匀强磁场,第一次将线框从磁场中以速度v匀速拉出,第二次让线框以ω=2v/b的角速度转过90°角。那么
A.通过导线横截面积的电量q1:q2=1:nB.通过导线横截面积的电量q1:q2=1:1
C.线框发热功率P1:P2=2n:1D.线框发热功率P1:P2=2:1
[解析]首先,显见在第一、二次运动过程中,磁通量的减少为。当回路为n匝,总电阻为R时,由依据㈣(另一重要推论)可得。故知A错而B对。
然后,显然两种情况下线框电阻不变。从而,由电(热)功率公式可得
;
又应用依据㈡⑵和依据㈡⑶,可得
联立①②③式,即可求出以下结果
故知C错而D对。因此,本题答案为:B、D。
[点拨]应用另一“重要推论”解决问题时,必须注意到公式原形是对于单匝回路而言,其中R为单匝回路的电阻。求第二种情况下的动生电动势,实则应用了公式。
[例题12](’05天津)将硬导线中间一段折成不封闭的正方形,每边长为l,它在磁感应强度为B、方向如—15图的匀强磁场中匀速转动,转速为n,导线在a、b两处通过电刷与外电路连接,外电路有额定功率为P的小灯泡并正常发光,电路中除灯泡外,其余部分的电阻不计,灯泡的电阻应为()
A.(2πl2nB)2/P
B.2(πl2nB)2/P
C.(l2nB)2/2P
D.(l2nB)2/P
[解析]类似地,由依据㈡⑶、角速-转速关系得
又,由电功率公式可得
联立①②③式,我们即可求出灯泡的电阻
因此,本题答案为:B。
[点拨]在这里,由于讨论方形“回路”转动的原因,因此多采用圆周运动的知识(注:角速-转速关系,其中n必须取单位r/min)。
[例题13](’07高考模拟)如图—16所示,一矩形线圈abcd的面积S为,它与匀强磁场方向之间的夹角θ为30°,穿过线圈的磁通量Φ为,则磁场的磁感应强度B=_________T。若线圈在0.1s时间内以ab边为轴翻转180°,则此过程中线圈的平均电动势_________V.
[解析]首先,依题设,应用磁通量计算公式可得
其次,若规定自左向右为磁通正方向,则转过180°时穿过线圈的磁通必定为负。从而,由磁通变化的定义得其“减小”为
然后,再应用感生电动势公式,不难得到
最后,根据“增反减同”规律结合安培定则,可以断定水平向右看,其方向为顺时针的。
因此,本题答案为:0.2T,2×10-2V。
[点拨]选择本例的意义在于,一则强调磁通的方向性和非矢量性,二则强调如何计算磁通和磁通的变化量。应该明确,在“磁学”部分内容中,他如合磁通的“意义和计算”也是十分重要的。
“切导回路”在磁场中的转动产生动生电动势的典型问题的分析和解决,详见后文“交变电流”的有关内容。并且,当“切导回路”在磁场中振动时,也可产生动生电动势和动生电流.
图—1
θ
图—3
图—2
图—4
图—5
图—6
图—7
图—8
图—9
图—10
图—11
图—12
图—13
M
N
v
ω,
a,
b
图—14
图—15
30°
B
a
b
c
d
图—16
在电磁感应现象中,部分导体或可导回路往往会相对于磁场做切割磁感线的运动。我们可以把此导体或可导回路称作“切割导体”,简称“切导”。
所谓动生电动势,指与磁场做相对、切割磁感线的运动“切导”中产生的感应电动势。这里应该强调,产生动生电动势必须具备两个必要条件,即一则“切导”与磁场有相对运动现象发生;二则该“切导”必须切割磁感线。实际上,“切导”的定义本身即包含着这两方面的意义。
一、破解依据
欲解决此类问题,大致归纳为以下几条“依据”:
㈠产生动生电动势的条件(略).
㈡大小计算:⑴其中,n为回路匝数,为回路面积的变化率。
⑵,其中E、B、v等两两垂直,l可视为“有效(切割)长度”——部分或整体回路在垂直于磁场方向的“投影长度”。⑶,其中为动生电动势的最大值。⑷,其中,l做定轴转动。
㈢方向判定:“手心对N极、拇指表运动、四指示动(生)电(流)”——右手定则。与“手心对N极、四指表通电、拇指示受力”——左手定则显著不同。
㈣另一重要推论:其中q、R分别为流过单匝回路的电荷量及其电阻。
㈤“切导回路”与“磁场”的相互作用,对应“增反减同”规律则有“进则推拒,出却扯拉”,简称作“进推出拉”的规律。
㈥若涉及外电路变换、变化以及电流、电压、功率、效益等,则需综合应用“恒定电流”的有关概念和规律。
㈦若涉及冲动联系、动量定理、动量守恒与功能联系(如动能定理)、能量转化和守恒等等,则宜采用相应手段处理。
二、解题示例
所谓“切导回路”,即由正在做切割运动的导体组成的回路,如由金属组成的各种形式的线圈、线框等。在匀强磁场或有界匀强磁场中做平动的切导回路中,必定产生动生电动势。动生电动势的大小常常由于回路的“有效长度”或“面积变化”的不同而不同。
一、“切导回路”垂直于磁场方向的平动问题
若匀强磁场与“切导回路”所在平面垂直,其沿垂直于磁场方向自进入、于内到离开过程中,自然随之带来动生电动势、动生电流的有无确认、大小计算、方向判断以及功能分析、能量转换与守恒应用等等一系列问题。请读者看下面的典型例题的解决过程。
[例题1](’04江苏)如图—1所示,一个有界匀强磁场区域,磁场方向垂直纸面向外.一个矩形闭合导线框abcd,沿纸面由位置1(左)匀速运动到位置2(右).则
(A)导线框进入磁场时,感应电流方向为a→b→c→d→a
(B)导线框离开磁场时,感应电流方向为a→d→c→b→a
(C)导线框离开磁场时,受到的安培力方向水平向右
(D)导线框进入磁场时.受到的安培力方向水平向左
[解析]首先,当导线框“进入”磁场时,由“依据”㈠、㈢(右手定则)可知,动生(或感应)电流沿顺时针方向;“离开”时,则沿逆时针方向。故知选项A、B均错。
然后,由依据㈤(即“进推出拉”规律)(或左手定则),可判断“进入”时,安培力向左;“离开”时亦向左。故知选项C错而D对。
因此,本题答案为:D。
[点拨]应该强调,左手定则判“受力”,右手定则断“感电”;无论磁场、感应电流方向如何,因而“切导”所受安培力总与为运动“阻力”。
[例题2](’05全国Ⅰ)图中两条平行虚线之间存在匀强磁场,虚线间的距离为l,磁场方向垂直纸面向里。abcd是位于纸面内的梯形线圈,ad与bc间的距离也为l。t=0时刻,bc边与磁场区域边界重合(如图)。现令线圈以恒定的速度v沿垂直于磁场区域边界的方向穿过磁场区域。取沿a→b→c→d→a的感应电流为正,则在线圈穿越磁场区域的过程中,感应电流I随时间t变化的图线可能是()
[解析]首先,设梯形线圈的左底边长为l0,分析水平向右匀速“进入”、“离开“磁场时,易知其“有效长度”均为
其中。再设线圈电阻为R,由依据㈡⑵、欧姆定律可得电流大小
显然,I为t的一次函数,随时间增大而均匀增大。
然后,应用依据㈢,可知线圈“进入”则电流为负;“离开”则为正。
综上所述,可知本题答案为:B。
[例题3](’07全国Ⅰ)如图—4所示,LOO/L/为一折线,它所形成的两个角∠LOO/和∠OO/L/均为45°。折线的右边有一匀强磁场。其方向垂直于纸面向里。一边长为l的正方形导线框沿垂直于OO/的方向以速度v作匀速直线运动,在t=0的刻恰好位于图中所示位置。以逆时针方向为导线框中电流的正方向,在上面四幅图中能够正确表示电流-时(I-t)关系的是(时间以I/v为单位)
[解析]首先,正方形导线框在三段连续相等的时间内,其“有效长度”经历先增大至最大而迅即为零、后增至最大、再后由最大减小为零等非连续“均匀变化”过程。又由于“磁强”B、速度v等均未改变。由依据㈠、㈡,可知该切导回路的电动势的大小亦随之做类似变化。
然后,再应用依据㈢(右手定则)可知,电流方向经历先正、后负、再后亦负的变化过程。
因此,本题答案为:D。
[点拨]由例2、3解析可见,对匀强磁场中切导回路而言,欲求感应电动势的大小,先须求出回路的“有效长度”。
[例题4](’00全国)空间存在以ab、cd为边界的匀强磁场区域,磁感强度大小为B,方向垂直纸面向外,区域宽为l1。现有一矩框处在图中纸面内,它的短边与ab重合,长度为l2,长边的长度为2l1,如图—5所示,某时刻线框以初速v沿与ab垂直的方向进入磁场区域,同时某人对线框施以作用力,使它的速度大小和方向保持不变。设该线框的电阻为R。从线框开始进入磁场到完全离开磁场的过程中,人对线框作用力所做的功等于___________________。
[解析]首先,显见切导回路的有效切割长度为l2,切割运动的实际位移为2l1。从而,由“依据”㈡⑵、欧姆定律和安培力公式得
已知线框作匀速直线运动,因而其水平方向受力平衡,亦即人对线框作用力与安培力的“等大反向”,人对线框作用力所做的功大小等于安培力所做的功。设人所做的功为W。从而,可得
[点拨]前已说明,安培力总为“切导”运动的阻力;进而指出,安培力做功必定消耗系统的机械能(或曰电能),而此能量的减小表现为等量的热损耗。
[例题5](’06上海)如图—6所示,将边长为a、质量为m、电阻为R的正方形导线框竖直向上抛出,穿过宽度为b、磁感应强度为B的匀强磁场,磁场的方向垂直纸面向里.线框向上离开磁场时的速度刚好是进人磁场时速度的一半,线框离开磁场后继续上升一段高度,然后落下并匀速进人磁场。整个运动过程中始终存在着大小恒定的空气阻力f且线框不发生转动。求:
⑴线框在下落阶段匀速进人磁场时的速度v2;
⑵线框在上升阶段刚离开磁场时的速度v1;
⑶线框在上升阶段通过磁场过程中产生的焦耳热Q。
[解析]⑴首先,线框之所以在下落阶段匀速进入,一定是在竖直方向受力平衡。从而,则有
由此解得
⑵其次,在线框离开磁场的上升阶段、下落阶段,由动能定理可得
联立①②③式,即可求出
⑶然后,已知线框穿越磁场进入、离开时的速度分别为v1、v2。从而,由功能关系可得
联立④⑤⑥式,我们即可求出线框在上升阶段通过磁场过程中产生的焦耳热
[点拨]应该说明,在讨论“切导”在磁场中的运动时,对系统的受力、运动、功能等三种分析是完全必要的。由解析可见,动能定理、功能关系在这里起了至关重要的作用。
[例题6](’07重庆)t=0时,磁场在xOy平面内的分布如题—7图所示。其磁感应强度的大小均为B0,方向垂直于xOy平面,相邻磁场区域的磁场方向相反。每个同向磁场区域的宽度均为l0。整个磁场以速度v沿x轴正方向匀速运动。
⑴若在磁场所在区间,xOy平面内放置一由a匝线圈串联而成的矩形导线框abcd,线框的bc边平行于x轴。bc=l0、ab=L,总电阻为R,线框始终保持静止。求
①线框中产生的总电动势大小和导线中的电流大小;
②线框所受安培力的大小和方向。
⑵该运动的磁场可视为沿x轴传播的波,设垂直于纸面向外的磁场方向为正,画出L=0时磁感应强度的波形图,并求波长和频率f。
[解析]⑴①首先,已知切割磁感线的速度为v,由依据㈡任意时刻线框中电动势大小
再由欧姆定律,即可求出导线中的电流大小
②其次,应用安培力公式可得线框所受安培力F的大小
再由左手定则判断,线框所受安培力的方向始终沿x轴正方向.
⑵然后,由波的知识可知,磁感应强度的波长和频率分别为
不难画出t=0时磁感应强度的波形图如图—8所示。
[点拨]在切导于磁场中平动的问题中,其所受安培力的大小,往往有的表达形式,只不过在这里有效长度扩大了两倍而已。第⑵小题显然应用了波长、波速和频率的关系式。
[例题7](’07江苏)如图—9所示,空间等间距分布着水平方向的条形匀强磁场,竖直方向磁场区域足够长,磁感应强度B=1T,每一条形磁场区域的宽度及相邻条形磁场区域的间距均为d=0.5m,现有一边长l=0.2m、质量m=0.1kg、电阻R=0.1Ω的正方形线框MNOP以v0=7m/s的初速从左侧磁场边缘水平进入磁场,求
⑴线框MN边刚进入磁场时受到安培力的大小F。
⑵线框从开始进入磁场到竖直下落的过程中产生的焦耳热Q。
⑶线框能穿过的完整条形磁场区域的个数n。
[解析]⑴首先,分析可知当线框MN边刚进入磁场区域做切割磁感线运动时,线框MN边中必定产生动生电动势、动生电流。从而,由“依据”㈡⑵、欧姆定律、安培力公式可得
联立①②③式,代如已知数据,即可求出此时受到安培力的大小
⑵其次,在线框从开始进入磁场到竖直下落的过程中,重力做正功而电能转变为电热。设线框竖直下落时,线框下落了h,速度为vt,从而由自由落体运动规律、功能关系可得
联立④⑤式,可求出过程中产生的焦耳热为
⑶然后,由于只有在线框进入和穿出条形磁场区域时,才产生感应电动势。从而,由“依据”㈡⑵、欧姆定律和安培力公式,可得线框部分进入磁场区域x时所受的安培力为
由此可见,安培力是速度的函数。欲求穿过的完整条形磁场区域的个数n,尝试在t→t+△t时间内应用动量定理。由此,可得
以后,在时间t或磁场区域x内,对②式求和可得
由③式即可解得
显然
最后代入已知数据,我们可以求出
即线框能穿过的完整条形磁场区域的个数为4个。
[点拨]此例应为一道力、热、电综合性极强、难度亦较大的高考试题,属于此类问题中的佼佼者。动量定理的必要、巧妙的引入和应用,令人开扩眼界和痛感欣慰。若换一方式,从讨论线框穿过第1个条形磁场过程入手。先取其平均感应电动势为,类似地,可得平均力的冲量。显然,平均力冲量是恒量,与穿越时间无关。依次类推,穿越n个条形磁场则皆然。从而,由动量定理得。进而可求出相同的结果。
二、“切导回路”垂直于磁场的另一种平动问题。
若匀强磁场与“切导回路”平面“平行”,当其沿垂直于磁场方向平动时,类似地,亦随之带来一系列动生电动势、动生电流等等相应问题。
下面,我们先来讨论由笔者编制的一道“08高考预测题”。
[例题8](’08自编预测)如图—10所示,一环形磁铁的外管、内柱分别为N极、S极,之间的区域可视为辐向分布的匀强磁场,磁感应强度为B。现垂直于磁场方向放入一个匝数为n、半径为r、导线单位长度的电阻为的圆形线圈。试求:⑴当线圈以速度v垂直于纸面向内运动时,动生电动势的大小和方向?⑵设通过线圈的恒定电流为I,线圈的机械功率多大?⑶若线圈垂直于纸面振动,其瞬时速度表达式为,动生电流的功率。
[解析]⑴首先,显见回路的“有效切割长度”等于回路的周长,即。
由依据㈡、㈢(即动生电动势公式和右手定则)可得
显见,线圈的动生电动势(或动生电流)方向为逆时针的。
⑵其次,设线圈的机械功率为P,则由功率关系、电阻计算式得
联立①②③式,即可求出
⑶然后,欲求电流的功率,须求电动势、电流的有效值。从而,由依据㈡可得电动势的最大值
进而,设I/、E/为电流、电动势的有效值,p/为动生电流的功率。由交变电流知识可得
最后,联立③④⑤式,即可求出以下结果
[点拨]假如在该磁场中,放入垂直于纸面的长为L金属棒,当其绕O点匀或变速转动时,由依据㈡可得,再结合左手定则,我们仍不难求出其动生电动势的大小和方向。
[例题9](’07北京)用密度为d.电阻率为、横截面积为A的薄金属条制成边长为L的闭合正方形框。如图—11所示,金属方框水平放在磁极的狭缝间,方框平面与磁场方向平行。设匀强磁场仅存在于相对磁极之间,其他地方的磁场忽略不计。可认为方框的边和边都处在磁极之间,极间磁感应强度大小为B。方框从静止开始释放,其平面在下落过程中保持水平(不计空气阻力)。
⑴求方框下落的最大速度vm(设磁场区域在竖直方向足够长);
⑵当方框下落的加速度为时,求方框的发热功率P;
⑶已知方框下落时间为t时,下落高度为h,其速度为vt(vt
再由质量计算式、电阻定律等,可知
其次,由①②③式、牛二定律可得
当加速度等于零时,即当时,方框达到最大速度vm。亦即
由此可得,方框下落的最大速度
⑵然后,当方框下落加速度为时,再由牛二定律、电功率公式得
联立②③⑥⑦式,即可求出方框的发热功率
⑶最后,根据能量守恒定律,可得
再联立②③⑧式,即可求出恒定电流的表达式
[点拨]应该指出,欲求方框的最大速度,必须先应用牛二定律写出加速度的瞬时表达式,再由物体的速度变化的规律可知,“加速度为零”是速度达到最大的必要条件。与力学问题不同的是,求合力必须考虑“通导”所受的安培力。而能量守恒则为重力势能的减少等于动能、内能的增加(转为热量放出)。
三、“切导回路”在匀强磁场中的转动(或振动)问题
以下几例为由于“切导回路”在有界磁场中转动,从而产生动生电动势的问题。
[例题10](经典试题)半径为r、质量为m、电阻为R的金属圆环,用一根长为L的绝缘细绳悬挂于O点,宽度为L/4的垂直向里的匀强磁场的上边界到O点的距离为L/2,如图—12所示。现使圆环由与悬点等高的A点由静止释放,若运动过程中圆环所在平面始终垂直于磁场,则圆环产生的焦耳热是()
A.mgLB.mg(L/2+r)C.mg(3L/4+r)D.mg(L+2r)
[解析]首先,分析环的运动过程,可知每当金属圆环进入、离开磁场时,由依据㈢(右手定则)、左手定则可知其均受阻力——安培力的作用。因此由功能关系可知,环的机械能将不断减少,减少的机械能则转化为焦耳热。
然后,显见当环运动到磁场下边界之外,亦即如图—13的位置时,环不再切割磁感应线而安培力消失,故知此后机械能即不再减少,亦不会再有焦耳热产生。从而,由功能关系可得
因此,本题答案为:C。
[点拨]我们又一次看到,当“切导回路”进、出磁场时,由于受“进推出拉”的安培阻力故使系统的机械能减少,其实则转化为焦耳热。
[例题11](’07枣庄调研)长为a、宽为b的矩形线框有n匝,每匝线圈电阻为R。如图—14所示,对称轴MN的左侧有磁感应强度为B的匀强磁场,第一次将线框从磁场中以速度v匀速拉出,第二次让线框以ω=2v/b的角速度转过90°角。那么
A.通过导线横截面积的电量q1:q2=1:nB.通过导线横截面积的电量q1:q2=1:1
C.线框发热功率P1:P2=2n:1D.线框发热功率P1:P2=2:1
[解析]首先,显见在第一、二次运动过程中,磁通量的减少为。当回路为n匝,总电阻为R时,由依据㈣(另一重要推论)可得。故知A错而B对。
然后,显然两种情况下线框电阻不变。从而,由电(热)功率公式可得
;
又应用依据㈡⑵和依据㈡⑶,可得
联立①②③式,即可求出以下结果
故知C错而D对。因此,本题答案为:B、D。
[点拨]应用另一“重要推论”解决问题时,必须注意到公式原形是对于单匝回路而言,其中R为单匝回路的电阻。求第二种情况下的动生电动势,实则应用了公式。
[例题12](’05天津)将硬导线中间一段折成不封闭的正方形,每边长为l,它在磁感应强度为B、方向如—15图的匀强磁场中匀速转动,转速为n,导线在a、b两处通过电刷与外电路连接,外电路有额定功率为P的小灯泡并正常发光,电路中除灯泡外,其余部分的电阻不计,灯泡的电阻应为()
A.(2πl2nB)2/P
B.2(πl2nB)2/P
C.(l2nB)2/2P
D.(l2nB)2/P
[解析]类似地,由依据㈡⑶、角速-转速关系得
又,由电功率公式可得
联立①②③式,我们即可求出灯泡的电阻
因此,本题答案为:B。
[点拨]在这里,由于讨论方形“回路”转动的原因,因此多采用圆周运动的知识(注:角速-转速关系,其中n必须取单位r/min)。
[例题13](’07高考模拟)如图—16所示,一矩形线圈abcd的面积S为,它与匀强磁场方向之间的夹角θ为30°,穿过线圈的磁通量Φ为,则磁场的磁感应强度B=_________T。若线圈在0.1s时间内以ab边为轴翻转180°,则此过程中线圈的平均电动势_________V.
[解析]首先,依题设,应用磁通量计算公式可得
其次,若规定自左向右为磁通正方向,则转过180°时穿过线圈的磁通必定为负。从而,由磁通变化的定义得其“减小”为
然后,再应用感生电动势公式,不难得到
最后,根据“增反减同”规律结合安培定则,可以断定水平向右看,其方向为顺时针的。
因此,本题答案为:0.2T,2×10-2V。
[点拨]选择本例的意义在于,一则强调磁通的方向性和非矢量性,二则强调如何计算磁通和磁通的变化量。应该明确,在“磁学”部分内容中,他如合磁通的“意义和计算”也是十分重要的。
“切导回路”在磁场中的转动产生动生电动势的典型问题的分析和解决,详见后文“交变电流”的有关内容。并且,当“切导回路”在磁场中振动时,也可产生动生电动势和动生电流.
图—1
θ
图—3
图—2
图—4
图—5
图—6
图—7
图—8
图—9
图—10
图—11
图—12
图—13
M
N
v
ω,
a,
b
图—14
图—15
30°
B
a
b
c
d
图—16
同课章节目录
