苏科版七年级下册数学第七章平面图形的认识(二)单元综合检测试卷(含答案)
文档属性
| 名称 | 苏科版七年级下册数学第七章平面图形的认识(二)单元综合检测试卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 265.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-24 00:00:00 | ||
图片预览



文档简介
第七章平面图形的认识(二)
一、选择题
1.如图所示是“福娃欢欢”的五幅图案,②,③,④,⑤哪一个图案可以通过平移图案①得到(? )
A.?②?????????????????????????????????????????B.?③?????????????????????????????????????????C.?④?????????????????????????????????????????D.?⑤
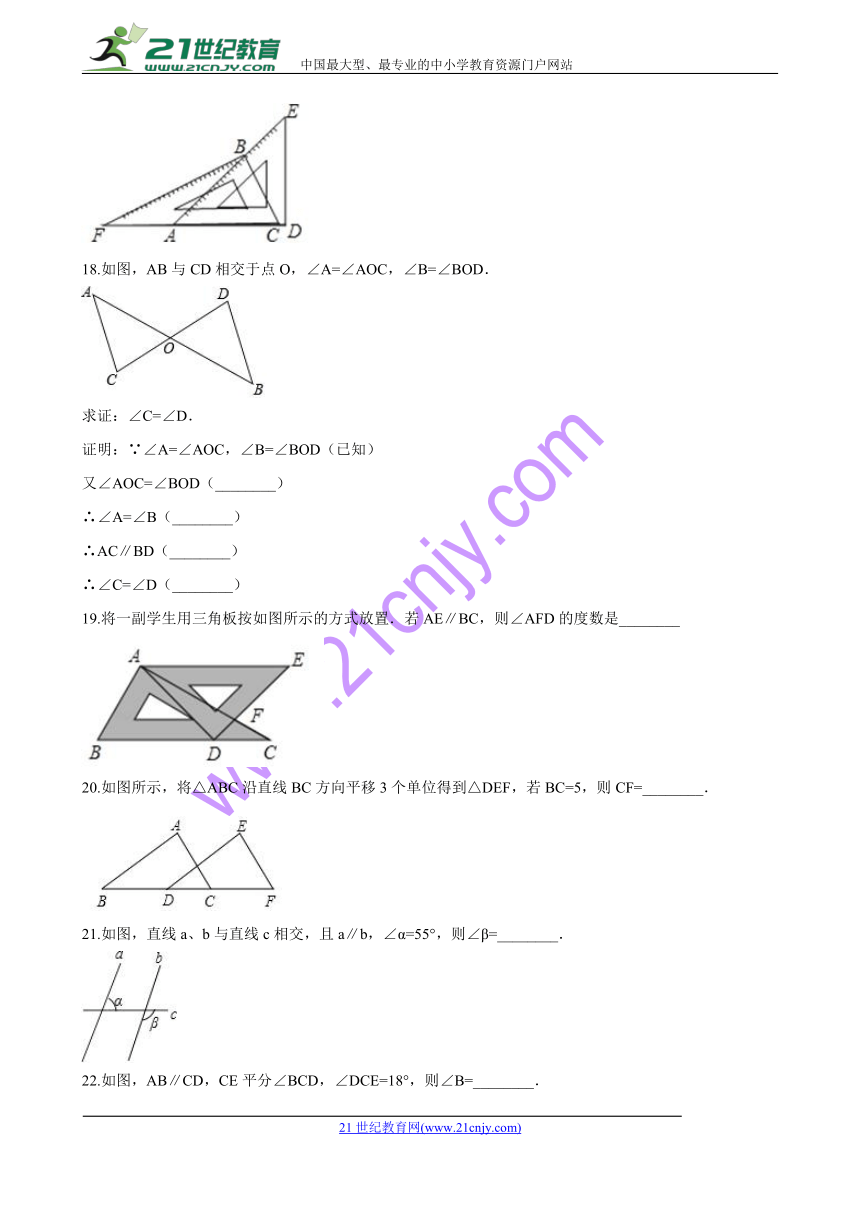
2.在平移过程中,对应线段( )
A.?互相垂直且相等???????????????B.?互相平行且相等???????????????C.?相互平行一相等???????????????D.?相等但不平行
3.小明有两根3cm、7cm的木棒,他想以这两根木棒为边做一个三角形,还需再选用的木棒长为( )
A.?3cm????????????????????????????????????B.?4cm????????????????????????????????????C.?9cm????????????????????????????????????D.?10cm
4.如图,∠1=100°,要使a∥b,必须具备的另一个条件是(?? )
A.?∠2=100°????????????????????????????B.?∠3=80°????????????????????????????C.?∠3=100°????????????????????????????D.?∠4=80°
5.下列关于三角形的说法错误的是(?? )
A.?三边高线的交点一定在三角形内部??????????????????????B.?三条中线的交点在三角形内部 C.?三条平分线的交点在三角形内部?????????????????????????D.?以上说法均正确21世纪教育网版权所有
6. 如图,已知直线AB∥CD,直线EF与AB、CD相交于N,M两点,MG平分∠EMD,若∠BNE=30°,则∠EMG等于( ) 【版权所有:21教育】
A.?15°?????????????????????????????????????B.?30°??????????????????????????????????????C.?75°??????????????????????????????????????D.?150°
7.如图所示,若a∥b,∠1=120°,则∠2=(?? )
A.?55°???????????????????????????????????????B.?60°???????????????????????????????????????C.?65°???????????????????????????????????????D.?75°
8.能够将一个三角形的面积平分的线段是(?? )
A.?一边上的高线?????????????B.?一个内角的角平分线?????????????C.?一边上的中线?????????????D.?一边上的中垂线
9.如图,点E在BC的延长线上,则下列条件中,能判定AD∥BC的是(?? )
A.?∠B=∠DCE????????????????????????B.?∠3=∠4????????????????????????C.?∠1=∠2????????????????????????D.?∠D+∠DAB=180°
10.如图,a∥b,将三角尺的直角顶点放在直线a上,若∠1=50°,则∠2的度数为( )
A.?30°????????????????????????????????????????B.?40°??????????????????????????????????????C.?50°??????????????????????????????????????D.?60°
11.如图,已知直线a,b被直线c所截,那么∠1的内错角是( )
A.?∠2???????????????????????????????????????B.?∠3????????????????????????????????????????C.?∠4????????????????????????????????????????D.?∠5
12.如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果∠1=15°,那么∠2的度数是(?? ) 21教育网
A.?15°???????????????????????????????????????B.?25°???????????????????????????????????????C.?30°???????????????????????????????????????D.?35°
二、填空题
13.如图两线段l1 , l2被直线l3所截,图中同位角的对数与内错角的对数的和是________?. 21·cn·jy·com
14.将直尺和直角三角板按如图方式摆放,已知∠1=30°,则∠2的大小是________.
15.已知△ABC的两条边的长度分别为3cm,6cm,若△ABC的周长为偶数,则第三条边的长度是________?cm. 21·世纪*教育网
16.完成下面推理过程. 如图:在四边形ABCD中,∠A=106°﹣α,∠ABC=74°+α,BD⊥DC于点D,EF⊥DC于点F,求证:∠1=∠2 证明:∵∠A=106°﹣α,∠ABC=74°+α(已知) ∴∠A+∠ABC=180° ∴AD∥________???(________) ∴∠1=________????(________) ∵BD⊥DC,EF⊥DC(已知) ∴∠BDF=∠EFC=90°(________) ∴BD∥________???(________) ∴∠2=________????(________) ∴∠1=∠2(________) www-2-1-cnjy-com
17.如图,把一副常用的三角板如图所示拼在一起,那么图中∠ABF=________?
18.如图,AB与CD相交于点O,∠A=∠AOC,∠B=∠BOD. 求证:∠C=∠D. 证明:∵∠A=∠AOC,∠B=∠BOD(已知) 又∠AOC=∠BOD(________) ∴∠A=∠B(________) ∴AC∥BD(________) ∴∠C=∠D(________) 2-1-c-n-j-y
19.将一副学生用三角板按如图所示的方式放置.若AE∥BC,则∠AFD的度数是________? 【来源:21·世纪·教育·网】
20.如图所示,将△ABC沿直线BC方向平移3个单位得到△DEF,若BC=5,则CF=________. 【来源:21cnj*y.co*m】
21.如图,直线a、b与直线c相交,且a∥b,∠α=55°,则∠β=________.
22.如图,AB∥CD,CE平分∠BCD,∠DCE=18°,则∠B=________.
三、解答题
23.图中的∠1与∠C、∠2与∠B、∠3与∠C,各是哪两条直线被哪一条直线所截形成的同位角?
24.如图(1)将△ABD平移,使D沿BD延长线移至C得到△A′B′D′,A′B′交AC于E,AD平分∠BAC. (1)猜想∠B′EC与∠A′之间的关系,并写出理由. (2)如图将△ABD平移至如图(2)所示,得到△A′B′D′,请问:A′D平分∠B′A′C吗?为什么? 21cnjy.com
25.直线MN与直线PQ垂直相交于O,点A在直线PQ上运动,点B在直线MN上运动.
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值. www.21-cn-jy.com
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F,在△AEF中,如果有一个角是另一个角的3倍,试求∠ABO的度数. 2·1·c·n·j·y
参考答案
一、选择题
D B C C A A B C B B B C
二、填空题
13. 6 14. 60° 15. 5或7
16. BC;同旁内角互补,两直线平行;∠DBC;两直线平行,内错角相等;垂直的定义;EF;同位角相等,两直线平行;∠DBC;两直线平行,同位角相等;等量代换 21*cnjy*com
17. 15°
18. 对顶角相等;等量代换;内错角相等,两直线平行;两直线平行,内错角相等.
19. 75° 20. 3 21. 125 22. 36°
三、解答题
23. ∠1与∠C是直线DE、BC被直线AC所截形成的同位角,∠2与∠B是直线DE、BC被直线AB所截形成的同位角,∠3与∠C是直线DF、AC被直线BC所截形成的同位角. 【出处:21教育名师】
24. 解:(1)∠B′EC=2∠A′, 理由:∵将△ABD平移,使D沿BD延长线移至C得到△A′B′D′,A′B′交AC于E,AD平分∠BAC, ∴∠BAD=∠DAC,∠BAD=∠A′,AB∥A′B′, ∴∠BAC=∠B′EC, ∴∠BAD=∠A′=∠BAC=∠B′EC, 即∠B′EC=2∠A′; (2)A′D′平分∠B′A′C, 理由:∵将△ABD平移至如图(2)所示,得到△A′B′D′, ∴∠B′A′D′=∠BAD,AB∥A′B′, ∴∠BAC=∠B′A′C, ∵∠BAD=∠BAC, ∴∠B′A′D′=∠B′A′C, ∴A′D′平分∠B′A′C. 21教育名师原创作品
25. (1)解:∠AEB的大小不变, ∵直线MN与直线PQ垂直相交于O, ∴∠AOB=90°, ∴∠OAB+∠OBA=90°, ∵AE、BE分别是∠BAO和∠ABO角的平分线, ∴∠BAE= ∠OAB,∠ABE= ∠ABO, ∴∠BAE+∠ABE= (∠OAB+∠ABO)=45°, ∴∠AEB=135°; (2)解:∠CED的大小不变. 延长AD、BC交于点F. ∵直线MN与直线PQ垂直相交于O, ∴∠AOB=90°, ∴∠OAB+∠OBA=90°, ∴∠PAB+∠MBA=270°, ∵AD、BC分别是∠BAP和∠ABM的角平分线, ∴∠BAD= ∠BAP,∠ABC= ∠ABM, ∴∠BAD+∠ABC= (∠PAB+∠ABM)=135°, ∴∠F=45°, ∴∠FDC+∠FCD=135°, ∴∠CDA+∠DCB=225°, ∵DE、CE分别是∠ADC和∠BCD的角平分线, ∴∠CDE+∠DCE=112.5°, ∴∠E=67.5°; (3)解:(3)∵∠BAO与∠BOQ的角平分线相交于E, ∴∠EAO= ∠BAO,∠EOQ= ∠BOQ, ∴∠E=∠EOQ﹣∠EAO= (∠BOQ﹣∠BAO)= ∠ABO, ∵AE、AF分别是∠BAO和∠OAG的角平分线, ∴∠EAF=90°.? 在△AEF中, ∵有一个角是另一个角的3倍,故有: ①∠EAF=3∠E,∠E=30°,∠ABO=60°; ②∠EAF=3∠F,∠E=60°,∠ABO=120°; ③∠F=3∠E,∠E=22.5°,∠ABO=45°; ④∠E=3∠F,∠E=67.5°,∠ABO=135°. ∴∠ABO为60°或45°. 21*cnjy*com
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
