2018年高考理数考前20天终极冲刺攻略+统计
文档属性
| 名称 | 2018年高考理数考前20天终极冲刺攻略+统计 |  | |
| 格式 | zip | ||
| 文件大小 | 808.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-05-25 22:46:03 | ||
图片预览




文档简介
核心考点解读——统计
抽样方法(I)
用样本估计总体(II)
两个变量的线性相关(II)
1.从考查题型来看,选择题、填空题与解答题并重,并各有侧重,选择题、填空题中以考查抽样方法和用样本估计总体为主,兼顾两个变量的线性相关;解答题中则重点考查求回归直线方程及独立性检验.
2.从考查内容来看,主要考查抽样方法的选择,利用频率分布直方图、茎叶图等图表分析众数、中位数、平均数等数字特征,两个变量之间的线性相关等.
3.从考查热点来看,用样本估计总体是高考命题的热点,频率分布直方图、茎叶图、众数、中位数、平均数等是考查的重点,要能够对数据进行分析,然后对总体作简单、准确的评价.
1.抽样方法
(1)抽样方法包括:简单随机抽样、系统抽样、分层抽样.
它们的共同点是抽样过程中每个个体被抽到的可能性相等,都是(:个体总数,:抽取的样本个体数);每次抽出个体后不再将其放回,即是不放回地逐个抽样.
不同点是简单随机抽样是从总体中逐个抽取个体,适用于总体个数较少的情况;系统抽样是总体个数较多,将总体分成几部分,按预先制定的规则在各部分中抽取,其中起始部分抽样采用简单随机抽样;分层抽样是指总体由差异比较明显的几部分组成,则在这几部分中分层进行抽样,各层抽样采用简单随机抽样.
简单随机抽样常采用的方法有抽签法与随机数法.
2.用样本估计总体
(1)用样本的频率分布估计总体的频率分布
主要的图表:频率分布表、频率分布直方图、茎叶图.
优缺点:
频率分布表:在数量表示上比较确切,但不够直观、形象,分析数据分布的主体趋势不太方便;
频率分布直方图:能够很容易表示大量数据,非常直观地表明分布的形状,但得不出原始的数据内容;
茎叶图:所有的数据信息都可以从茎叶图中得到,同时便于记录和读取,能够展示数据的分布情况,但当样本数据较多或数据位数较多时,就显得不太方便.
(2)用样本的数字特征估计总体的数字特征
主要的数字特征:众数、中位数、平均数、极差、标准差和方差,要能从样本数据中找到众数与中位数,能够利用公式计算平均数、极差、标准差.
平均数:,
极差:样本数据的最大值与最小值的差,
标准差:.
(3)由频率分布直方图进行相关计算时,需掌握这些公式:,.注意频率分布直方图的纵坐标是,而不是频率.
3.两个变量的线性相关
(1)相关关系:正相关、负相关.
正相关:因变量随自变量的增大而增大;
负相关:因变量随自变量的增大而减小.
(2)若两个变量之间具有线性相关关系,则点散布在一条直线附近,该直线为回归直线,能够用最小二乘法求回归直线方程,能够利用相关系数来表明两个变量的线性相关性的强弱.
求回归直线方程的步骤:先依据样本数据画出散点图,确定两个变量具有线性相关关系;然后计算出的值;再计算回归系数,由此写出回归直线方程:.
(3)能够进行独立性检验
独立性检验的一般步骤:
i)根据样本数据列出列联表;
ii)计算随机变量的观测值,查下表确定临界值:
iii)如果,就推断“与有关系”,这种推断犯错误的概率不超过;否则,就认为在犯错误的概率不超过的前提下不能推断“与有关系”.
1.(2017高考新课标III,理3)某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.
根据该折线图,下列结论错误的是
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
2.(2016高考新课标III,理4)某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图.图中A点表示十月的平均最高气温约为15C,B点表示四月的平均最低气温约为5C.下面叙述不正确的是www.21-cn-jy.com
A.各月的平均最低气温都在0C以上
B.七月的平均温差比一月的平均温差大
C.三月和十一月的平均最高气温基本相同
D.平均最高气温高于20C的月份有5个
3.(2015高考新课标II,理3)根据下面给出的2004年至2013年我国二氧化硫排放量(单位:万吨)柱形图.以下结论中不正确的是【21·世纪·教育·网】
A.逐年比较,2008年减少二氧化硫排放量的效果最显著
B.2007年我国治理二氧化硫排放显现成效
C.2006年以来我国二氧化硫年排放量呈减少趋势
D.2006年以来我国二氧化硫年排放量与年份正相关
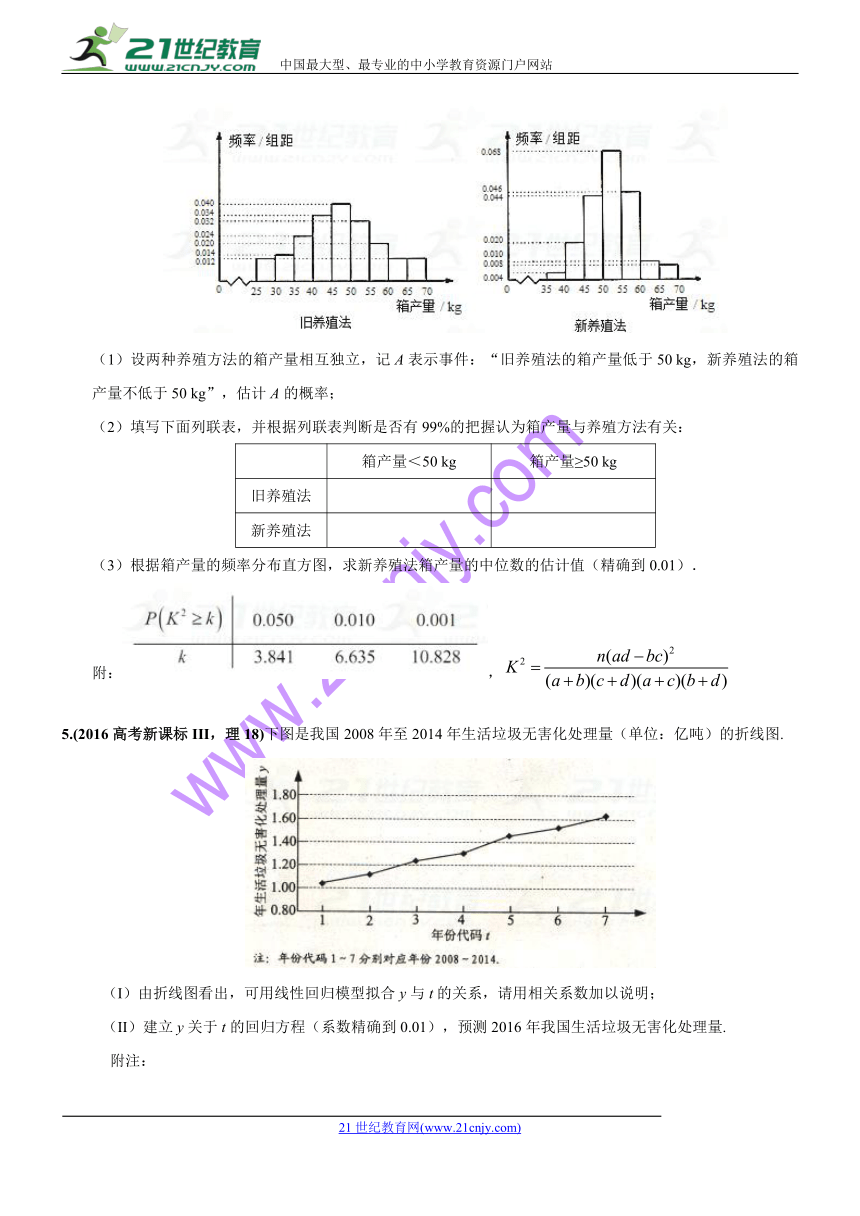
4.(2017高考新课标II,理18)海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100 个网箱,测量各箱水产品的产量(单位:kg).其频率分布直方图如下:www-2-1-cnjy-com
(1)设两种养殖方法的箱产量相互独立,记A表示事件:“旧养殖法的箱产量低于50 kg,新养殖法的箱产量不低于50 kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50 kg
箱产量≥50 kg
旧养殖法
新养殖法
(3)根据箱产量的频率分布直方图,求新养殖法箱产量的中位数的估计值(精确到0.01).
附:,
5.(2016高考新课标III,理18)下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.
(I)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(II)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据:,,,≈2.646.
参考公式:相关系数
回归方程中斜率和截距的最小二乘估计公式分别为:
6.(2015高考新课标II,理18)某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下:21*cnjy*com
A地区:62 73 81 92 95 85 74 64 53 76
78 86 95 66 97 78 88 82 76 89
B地区:73 83 62 51 91 46 53 73 64 82
48 65 81 74 56 54 76 65 79
(I)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,得出结论即可);
(II)根据用户满意度评分,将用户的满意度从低到高分为三个等级:
满意度评分
低于70分
70分到89分
不低于90分
满意度等级
不满意
满意
非常满意
记事件C:“A地区用户的满意度等级高于B地区用户的满意度等级”.假设两地区用户的评价结果相互独立.根据所给数据,以事件发生的频率作为相应事件发生的概率,求C的概率.2·1·c·n·j·y
7.(2015高考新课标I,理19)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的宣传费和年销售量数据作了初步处理,得到下面的散点图及一些统计量的值.
46.6
563
6.8
289.8
1.6
1469
108.8
表中= , =.
(I)根据散点图判断,与,哪一个适宜作为年销售量y关于年宣传费x的回归方程类型(给出判断即可,不必说明理由);【21教育】
(II)根据(I)的判断结果及表中数据,建立y关于x的回归方程;
(III)已知这种产品的年利润z与x,y的关系为 ,根据(II)的结果回答下列问题:
(i)年宣传费时,年销售量及年利润的预报值是多少?
(ii)年宣传费为何值时,年利润的预报值最大?
附:对于一组数据,,…,,其回归直线的斜率和截距的最小二乘估计分别为:,.
1.某学校在高一新生入学后的一次体检后,为了解学生的体质情况,决定从该校的名高一新生中采用系统抽样的方法抽取名学生进行体质分析,已知样本中第一个号为号,则抽取的第个学生的编号为
A. B.
C. D.
2.已知甲、乙两组数据的茎叶图如图所示,若它们的中位数相同,则甲组数据的平均数为
A.30 B.31
C.32 D.33
3.为了迎接2017年高考,了解学生的成绩状况,在一次省质检中,某省教育部门随机抽取了500名学生的数学考试成绩,统计如下表所示:21cnjy.com
成绩
人数
30
120
210
100
40
(1)计算各组成绩的频率,并填写在表中;
成绩
人数
30
120
210
100
40
频率
(2)已知本次质检数学测试的成绩,其中近似为样本的平均数,近似为样本方差,若该省有10万考生,试估计数学成绩在的人数;(以各组区间的中点值代表该组的取值)
(3)将频率视为概率,若从该省所有考生中随机抽取4人,记这4人中成绩在的人数为,求的分布列以及数学期望.21世纪教育网
参考数据:若,则,
,.
1.在一次数学测试中,唐老师对班上7名同学(记为…,7)第20题(满分12分)和第21题(满分12分)的得分情况进行统计,得分比(学生得分与满分的比值)如下图所示,其中第20题的得分比为图中虚线部分,第21题的得分比为图中实线部分.记第20题,第21题的平均得分分别为,第20题,第21题得分的标准差分别为,则21·世纪*教育网
A. B.
C. D.
2.近年来随着我国在教育科研上的投入不断加大,科学技术得到迅猛发展,国内企业的国际竞争力得到大幅提升.伴随着国内市场增速放缓,国内有实力的企业纷纷进行海外布局,第二轮企业出海潮到来.如在智能手机行业,国产品牌已在赶超国外巨头,某品牌手机公司一直默默拓展海外市场,在海外共设有多个分支机构,需要国内公司外派大量后、后中青年员工.该企业为了了解这两个年龄层的员工是否愿意被外派工作的态度,按分层抽样的方式从后和后的员工中随机调查了位,得到数据如下表:
愿意被外派
不愿意被外派
合计
后
后
合计
(1)根据调查的数据, 能否在犯错误的概率不超过0.1的前提下认为“是否愿意被外派与年龄有关”,并说明理由;【21教育名师】
(2)该公司举行参观驻海外分支机构的交流体验活动,拟安排名参与调查的后、后员工参加.后员工中有愿意被外派的人和不愿意被外派的人报名参加,从中随机选出人,记选到愿意被外派的人数为;后员工中有愿意被外派的人和不愿意被外派的人报名参加,从中随机选出人,记选到愿意被外派的人数为,求的概率.
参考数据:
参考公式:,其中.
真题回顾:
1.A【解析】观察折线图,每年7月到8月折线图呈下降趋势,月接待游客量减少,选项A说法错误;
折线图整体呈现出增长的趋势,年接待游客量逐年增加,选项B说法正确;
每年的接待游客量7,8月份达到最高点,即各年的月接待游客量高峰期大致在7,8月,选项C说法正确;
每年1月至6月的月折线图平稳,月接待游客量波动性更小,7月至12月折线图不平稳,月接待游客量波动性大,选项D说法正确.21教育网
2.D【解析】由题图可知各月的平均最低气温都在0C以上,A正确;由题图可知七月的平均温差大于7.5C,而一月的平均温差小于7.5C,所以七月的平均温差比一月的平均温差大,B正确;由题图可知三月和十一月的平均最高气温都大约在10C,基本相同,C正确;由题图可知平均最高气温高于20℃的月份有3个,所以不正确.故选D.
3.D
4.(1)记表示事件“旧养殖法的箱产量低于”,表示事件“新养殖法的箱产量不低于”,由题意知,旧养殖法的箱产量低于的频率为,故的估计值为0.62.
新养殖法的箱产量不低于的频率为,故的估计值为0.66.因此,事件A的概率估计值为.
(2)根据箱产量的频率分布直方图得列联表:
箱产量
箱产量
旧养殖法
62
38
新养殖法
34
66
的观测值,
由于,故有的把握认为箱产量与养殖方法有关.
(3)因为新养殖法的箱产量频率分布直方图中,箱产量低于的直方图面积为,箱产量低于的直方图面积为,故新养殖法箱产量的中位数的估计值为.21-cnjy*com
5.(I)由折线图中数据和附注中参考数据得,,,
,
. 因为与的相关系数近似为0.99,说明与的线性相关相当高,从而可以用线性回归模型拟合与的关系.
(II)由及(I)得,.所以,关于的回归方程为:.将2016年对应的代入回归方程得:.所以预测2016年我国生活垃圾无害化处理量将约1.82亿吨.
6.(I)两地区用户满意度评分的茎叶图如下
通过茎叶图可以看出,A地区用户满意度评分的平均值高于B地区用户满意度评分的平均值;A地区用户满意度评分比较集中,B地区用户满意度评分比较分散.【21cnj*y.co*m】
(II)记表示事件:“A地区用户的满意度等级为满意或非常满意”;
表示事件:“A地区用户的满意度等级为非常满意”;
表示事件:“B地区用户的满意度的等级为不满意”;
表示事件:“B地区用户的满意度的等级为满意”.
则与独立,与独立,与互斥,.
.
由所给数据得,,,发生的频率分别为,,,.故,
,,,故.
7.(I)由散点图可以判断,适宜作为年销售量关于年宣传费的回归方程类型.
(II)令,先建立关于的线性回归方程,由于==68,
∴=563?68×6.8=100.6,∴关于的线性回归方程为,因此关于的回归方程为.
(III)(ⅰ)由(II)知,当=49时,年销售量的预报值=576.6,年利润z的预报值为. 2-1-c-n-j-y
(ⅱ)根据(II)的结果知,年利润z的预报值,
所以当,即时,取得最大值.故年宣传费为46.24千元时,年利润的预报值最大.
名校预测
1.【答案】D【解析】由题意知组距为 则抽取学生的编号组成以7为首项,20为公差的等差数列,其通项公式为 故选D.21*教*育*名*师
2.【答案】B【解析】由茎叶图可知乙组数据的中位数为:,结合题意可知甲组数据的中位数为33,即,则甲组数据的平均数为:.故选B.
3. 【解析】(1)填表如下:
成绩
人数
30
120
210
100
40
频率
0.06
0.24
0.42
0.2
0.08
(2)依题意,,
故,
故,故, 故所求人数为(人).
(3)依题意,任取1人,成绩在的概率为,,,,,,
,所以的分布列为
0
1
2
3
4
故.
专家押题
1.【答案】C【解析】第20题,第21题的满分分值相同,由题图可知,7名同学第20题的得分比均高于第21题的得分比,所以第20题的平均得分高于第21题的平均得分,故;又由题图可知,第20题的得分比离散程度相对较小,所以第20题得分的标准差小于第21题得分的标准差,故.故选C.21·cn·jy·com
2.【解析】(1)计算得的观测值为
,
所以能在犯错误的概率不超过0.1的前提下认为“是否愿意被外派与年龄有关”.
(2)“”包含“”、“”、“”、
“”、“”、“”,共6个互斥事件,
且,,
,,
,,
所以.即的概率为.
抽样方法(I)
用样本估计总体(II)
两个变量的线性相关(II)
1.从考查题型来看,选择题、填空题与解答题并重,并各有侧重,选择题、填空题中以考查抽样方法和用样本估计总体为主,兼顾两个变量的线性相关;解答题中则重点考查求回归直线方程及独立性检验.
2.从考查内容来看,主要考查抽样方法的选择,利用频率分布直方图、茎叶图等图表分析众数、中位数、平均数等数字特征,两个变量之间的线性相关等.
3.从考查热点来看,用样本估计总体是高考命题的热点,频率分布直方图、茎叶图、众数、中位数、平均数等是考查的重点,要能够对数据进行分析,然后对总体作简单、准确的评价.
1.抽样方法
(1)抽样方法包括:简单随机抽样、系统抽样、分层抽样.
它们的共同点是抽样过程中每个个体被抽到的可能性相等,都是(:个体总数,:抽取的样本个体数);每次抽出个体后不再将其放回,即是不放回地逐个抽样.
不同点是简单随机抽样是从总体中逐个抽取个体,适用于总体个数较少的情况;系统抽样是总体个数较多,将总体分成几部分,按预先制定的规则在各部分中抽取,其中起始部分抽样采用简单随机抽样;分层抽样是指总体由差异比较明显的几部分组成,则在这几部分中分层进行抽样,各层抽样采用简单随机抽样.
简单随机抽样常采用的方法有抽签法与随机数法.
2.用样本估计总体
(1)用样本的频率分布估计总体的频率分布
主要的图表:频率分布表、频率分布直方图、茎叶图.
优缺点:
频率分布表:在数量表示上比较确切,但不够直观、形象,分析数据分布的主体趋势不太方便;
频率分布直方图:能够很容易表示大量数据,非常直观地表明分布的形状,但得不出原始的数据内容;
茎叶图:所有的数据信息都可以从茎叶图中得到,同时便于记录和读取,能够展示数据的分布情况,但当样本数据较多或数据位数较多时,就显得不太方便.
(2)用样本的数字特征估计总体的数字特征
主要的数字特征:众数、中位数、平均数、极差、标准差和方差,要能从样本数据中找到众数与中位数,能够利用公式计算平均数、极差、标准差.
平均数:,
极差:样本数据的最大值与最小值的差,
标准差:.
(3)由频率分布直方图进行相关计算时,需掌握这些公式:,.注意频率分布直方图的纵坐标是,而不是频率.
3.两个变量的线性相关
(1)相关关系:正相关、负相关.
正相关:因变量随自变量的增大而增大;
负相关:因变量随自变量的增大而减小.
(2)若两个变量之间具有线性相关关系,则点散布在一条直线附近,该直线为回归直线,能够用最小二乘法求回归直线方程,能够利用相关系数来表明两个变量的线性相关性的强弱.
求回归直线方程的步骤:先依据样本数据画出散点图,确定两个变量具有线性相关关系;然后计算出的值;再计算回归系数,由此写出回归直线方程:.
(3)能够进行独立性检验
独立性检验的一般步骤:
i)根据样本数据列出列联表;
ii)计算随机变量的观测值,查下表确定临界值:
iii)如果,就推断“与有关系”,这种推断犯错误的概率不超过;否则,就认为在犯错误的概率不超过的前提下不能推断“与有关系”.
1.(2017高考新课标III,理3)某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图.
根据该折线图,下列结论错误的是
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
2.(2016高考新课标III,理4)某旅游城市为向游客介绍本地的气温情况,绘制了一年中各月平均最高气温和平均最低气温的雷达图.图中A点表示十月的平均最高气温约为15C,B点表示四月的平均最低气温约为5C.下面叙述不正确的是www.21-cn-jy.com
A.各月的平均最低气温都在0C以上
B.七月的平均温差比一月的平均温差大
C.三月和十一月的平均最高气温基本相同
D.平均最高气温高于20C的月份有5个
3.(2015高考新课标II,理3)根据下面给出的2004年至2013年我国二氧化硫排放量(单位:万吨)柱形图.以下结论中不正确的是【21·世纪·教育·网】
A.逐年比较,2008年减少二氧化硫排放量的效果最显著
B.2007年我国治理二氧化硫排放显现成效
C.2006年以来我国二氧化硫年排放量呈减少趋势
D.2006年以来我国二氧化硫年排放量与年份正相关
4.(2017高考新课标II,理18)海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100 个网箱,测量各箱水产品的产量(单位:kg).其频率分布直方图如下:www-2-1-cnjy-com
(1)设两种养殖方法的箱产量相互独立,记A表示事件:“旧养殖法的箱产量低于50 kg,新养殖法的箱产量不低于50 kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50 kg
箱产量≥50 kg
旧养殖法
新养殖法
(3)根据箱产量的频率分布直方图,求新养殖法箱产量的中位数的估计值(精确到0.01).
附:,
5.(2016高考新课标III,理18)下图是我国2008年至2014年生活垃圾无害化处理量(单位:亿吨)的折线图.
(I)由折线图看出,可用线性回归模型拟合y与t的关系,请用相关系数加以说明;
(II)建立y关于t的回归方程(系数精确到0.01),预测2016年我国生活垃圾无害化处理量.
附注:
参考数据:,,,≈2.646.
参考公式:相关系数
回归方程中斜率和截距的最小二乘估计公式分别为:
6.(2015高考新课标II,理18)某公司为了解用户对其产品的满意度,从A,B两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下:21*cnjy*com
A地区:62 73 81 92 95 85 74 64 53 76
78 86 95 66 97 78 88 82 76 89
B地区:73 83 62 51 91 46 53 73 64 82
48 65 81 74 56 54 76 65 79
(I)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,得出结论即可);
(II)根据用户满意度评分,将用户的满意度从低到高分为三个等级:
满意度评分
低于70分
70分到89分
不低于90分
满意度等级
不满意
满意
非常满意
记事件C:“A地区用户的满意度等级高于B地区用户的满意度等级”.假设两地区用户的评价结果相互独立.根据所给数据,以事件发生的频率作为相应事件发生的概率,求C的概率.2·1·c·n·j·y
7.(2015高考新课标I,理19)某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费x(单位:千元)对年销售量y(单位:t)和年利润z(单位:千元)的影响,对近8年的宣传费和年销售量数据作了初步处理,得到下面的散点图及一些统计量的值.
46.6
563
6.8
289.8
1.6
1469
108.8
表中= , =.
(I)根据散点图判断,与,哪一个适宜作为年销售量y关于年宣传费x的回归方程类型(给出判断即可,不必说明理由);【21教育】
(II)根据(I)的判断结果及表中数据,建立y关于x的回归方程;
(III)已知这种产品的年利润z与x,y的关系为 ,根据(II)的结果回答下列问题:
(i)年宣传费时,年销售量及年利润的预报值是多少?
(ii)年宣传费为何值时,年利润的预报值最大?
附:对于一组数据,,…,,其回归直线的斜率和截距的最小二乘估计分别为:,.
1.某学校在高一新生入学后的一次体检后,为了解学生的体质情况,决定从该校的名高一新生中采用系统抽样的方法抽取名学生进行体质分析,已知样本中第一个号为号,则抽取的第个学生的编号为
A. B.
C. D.
2.已知甲、乙两组数据的茎叶图如图所示,若它们的中位数相同,则甲组数据的平均数为
A.30 B.31
C.32 D.33
3.为了迎接2017年高考,了解学生的成绩状况,在一次省质检中,某省教育部门随机抽取了500名学生的数学考试成绩,统计如下表所示:21cnjy.com
成绩
人数
30
120
210
100
40
(1)计算各组成绩的频率,并填写在表中;
成绩
人数
30
120
210
100
40
频率
(2)已知本次质检数学测试的成绩,其中近似为样本的平均数,近似为样本方差,若该省有10万考生,试估计数学成绩在的人数;(以各组区间的中点值代表该组的取值)
(3)将频率视为概率,若从该省所有考生中随机抽取4人,记这4人中成绩在的人数为,求的分布列以及数学期望.21世纪教育网
参考数据:若,则,
,.
1.在一次数学测试中,唐老师对班上7名同学(记为…,7)第20题(满分12分)和第21题(满分12分)的得分情况进行统计,得分比(学生得分与满分的比值)如下图所示,其中第20题的得分比为图中虚线部分,第21题的得分比为图中实线部分.记第20题,第21题的平均得分分别为,第20题,第21题得分的标准差分别为,则21·世纪*教育网
A. B.
C. D.
2.近年来随着我国在教育科研上的投入不断加大,科学技术得到迅猛发展,国内企业的国际竞争力得到大幅提升.伴随着国内市场增速放缓,国内有实力的企业纷纷进行海外布局,第二轮企业出海潮到来.如在智能手机行业,国产品牌已在赶超国外巨头,某品牌手机公司一直默默拓展海外市场,在海外共设有多个分支机构,需要国内公司外派大量后、后中青年员工.该企业为了了解这两个年龄层的员工是否愿意被外派工作的态度,按分层抽样的方式从后和后的员工中随机调查了位,得到数据如下表:
愿意被外派
不愿意被外派
合计
后
后
合计
(1)根据调查的数据, 能否在犯错误的概率不超过0.1的前提下认为“是否愿意被外派与年龄有关”,并说明理由;【21教育名师】
(2)该公司举行参观驻海外分支机构的交流体验活动,拟安排名参与调查的后、后员工参加.后员工中有愿意被外派的人和不愿意被外派的人报名参加,从中随机选出人,记选到愿意被外派的人数为;后员工中有愿意被外派的人和不愿意被外派的人报名参加,从中随机选出人,记选到愿意被外派的人数为,求的概率.
参考数据:
参考公式:,其中.
真题回顾:
1.A【解析】观察折线图,每年7月到8月折线图呈下降趋势,月接待游客量减少,选项A说法错误;
折线图整体呈现出增长的趋势,年接待游客量逐年增加,选项B说法正确;
每年的接待游客量7,8月份达到最高点,即各年的月接待游客量高峰期大致在7,8月,选项C说法正确;
每年1月至6月的月折线图平稳,月接待游客量波动性更小,7月至12月折线图不平稳,月接待游客量波动性大,选项D说法正确.21教育网
2.D【解析】由题图可知各月的平均最低气温都在0C以上,A正确;由题图可知七月的平均温差大于7.5C,而一月的平均温差小于7.5C,所以七月的平均温差比一月的平均温差大,B正确;由题图可知三月和十一月的平均最高气温都大约在10C,基本相同,C正确;由题图可知平均最高气温高于20℃的月份有3个,所以不正确.故选D.
3.D
4.(1)记表示事件“旧养殖法的箱产量低于”,表示事件“新养殖法的箱产量不低于”,由题意知,旧养殖法的箱产量低于的频率为,故的估计值为0.62.
新养殖法的箱产量不低于的频率为,故的估计值为0.66.因此,事件A的概率估计值为.
(2)根据箱产量的频率分布直方图得列联表:
箱产量
箱产量
旧养殖法
62
38
新养殖法
34
66
的观测值,
由于,故有的把握认为箱产量与养殖方法有关.
(3)因为新养殖法的箱产量频率分布直方图中,箱产量低于的直方图面积为,箱产量低于的直方图面积为,故新养殖法箱产量的中位数的估计值为.21-cnjy*com
5.(I)由折线图中数据和附注中参考数据得,,,
,
. 因为与的相关系数近似为0.99,说明与的线性相关相当高,从而可以用线性回归模型拟合与的关系.
(II)由及(I)得,.所以,关于的回归方程为:.将2016年对应的代入回归方程得:.所以预测2016年我国生活垃圾无害化处理量将约1.82亿吨.
6.(I)两地区用户满意度评分的茎叶图如下
通过茎叶图可以看出,A地区用户满意度评分的平均值高于B地区用户满意度评分的平均值;A地区用户满意度评分比较集中,B地区用户满意度评分比较分散.【21cnj*y.co*m】
(II)记表示事件:“A地区用户的满意度等级为满意或非常满意”;
表示事件:“A地区用户的满意度等级为非常满意”;
表示事件:“B地区用户的满意度的等级为不满意”;
表示事件:“B地区用户的满意度的等级为满意”.
则与独立,与独立,与互斥,.
.
由所给数据得,,,发生的频率分别为,,,.故,
,,,故.
7.(I)由散点图可以判断,适宜作为年销售量关于年宣传费的回归方程类型.
(II)令,先建立关于的线性回归方程,由于==68,
∴=563?68×6.8=100.6,∴关于的线性回归方程为,因此关于的回归方程为.
(III)(ⅰ)由(II)知,当=49时,年销售量的预报值=576.6,年利润z的预报值为. 2-1-c-n-j-y
(ⅱ)根据(II)的结果知,年利润z的预报值,
所以当,即时,取得最大值.故年宣传费为46.24千元时,年利润的预报值最大.
名校预测
1.【答案】D【解析】由题意知组距为 则抽取学生的编号组成以7为首项,20为公差的等差数列,其通项公式为 故选D.21*教*育*名*师
2.【答案】B【解析】由茎叶图可知乙组数据的中位数为:,结合题意可知甲组数据的中位数为33,即,则甲组数据的平均数为:.故选B.
3. 【解析】(1)填表如下:
成绩
人数
30
120
210
100
40
频率
0.06
0.24
0.42
0.2
0.08
(2)依题意,,
故,
故,故, 故所求人数为(人).
(3)依题意,任取1人,成绩在的概率为,,,,,,
,所以的分布列为
0
1
2
3
4
故.
专家押题
1.【答案】C【解析】第20题,第21题的满分分值相同,由题图可知,7名同学第20题的得分比均高于第21题的得分比,所以第20题的平均得分高于第21题的平均得分,故;又由题图可知,第20题的得分比离散程度相对较小,所以第20题得分的标准差小于第21题得分的标准差,故.故选C.21·cn·jy·com
2.【解析】(1)计算得的观测值为
,
所以能在犯错误的概率不超过0.1的前提下认为“是否愿意被外派与年龄有关”.
(2)“”包含“”、“”、“”、
“”、“”、“”,共6个互斥事件,
且,,
,,
,,
所以.即的概率为.
同课章节目录
